Моделирование динамической системы средствами функциональных грамматик

Конструктивное построение отображений между множествами слов, которые порождаются контекстно-свободными грамматиками, имеет большое практическое значение, поскольку контекстно-свободные грамматики являются гибкими инструментами для описания иерархических классификаций. Для разработки компьютерных программ, в которых присутствуют сложные объекты, необходима математическая модель вычислительных процессов, порождаемых программой.

Статья посвящена построению отображений между множествами, которые порождаются контекстно-свободными грамматиками. Такой подход дает возможность математически описывать компьютерную программу, моделирующую динамическую систему.

1    Постановка задачи

В работе рассматривается задача об уточнении понятия класса компьютерных программ, моделирующих динамическую систему. Решение этой задачи позволит исследовать структуру класса алгоритмов, моделирующих динамическую систему, и в той или иной степени сформулировать утверждения о поведении динамической системы, исследуя вычислительный процесс, изоморфный к функционированию динамической системы. Для такой постановки вопроса требуется построить формальную математическую модель класса компьютерных программ, моделирующих динамическую систему. Для построения математической модели компьютерной программы исследуется аппарат функциональных грамматик. Основной базисной операцией функциональных грамматик является операция отождествления, которая эффективна для построения алфавитных отображений над множествами слов, порождаемых контекстносвободными грамматиками. Используя построенную математическую модель языка программирования в виде универсальной алгебры ( M , Q ), строится конкретная формальная математическая модель программы, которая является компьютерной моделью функционирования динамической системы.

2    О построении отображений над множествами слов, порожденных контекстно-свободными грамматиками

Пусть задан конкретный и известный язык программирования L (Pascal, Си ++ и т. д.). Математическая модель языка программирования представляется в виде универсальной алгебры при помощи аппарата функциональных грамматик.

Основание функциональных грамматик состоит из следующих примитивов:

• 1.    Контекстно-свободная грамматика: алгоритм синтаксического анализа, выводы, сентенциональные фразы и выводы из них и т. д.

• 2.    Операция левого отождествления.

• 3.    Операция выбора «либо» | .

• 4.    Рекурсия.

• 5.    Многоуровневость G ₁ , G ₂ и т. д.

• 6.    Суперпозиция (есть дерево, в узлах которого стоят функции). Если функция, находящаяся в узле, дает результат, имеющий метатип знач , то данный результат передается по выходной ветви узла дерева как аргумент к следующей функции.

• 7.    Операция Eval (первый аргумент есть функция, второй аргумент — исходные данные этой функции). Eval применяет функцию к исходным данным и получает результат. Данный результат имеет метатип знач .

• 8.    Метатип знач является типом результата при выполнении функции.

• 9.    Метатип функ — тип композиций функций.

• 10.    Метатип текст — текст программы в заданном языке.

• 11.    Арифметические операции. В языке считаются заданными множество целых чисел; операции сложения, вычитания, умножения и целочисленного деления в десятичной арифметике и операции сравнения <, ≤, =, ≥, >.

С точки зрения универсальной алгебры язык L будет представлять собой конечную совокупность { Фi } _i ∈ , которая будет являться сигнатурой операций алгебры. Тогда любая программа x ∈ L будет представляться с помощью синтаксической грамматики G ₀ в виде суперпозиции базисных функций из сигнатуры алгебры { Фi } _i ∈ .

Если программа x не содержит синтаксических ошибок и синтаксический разбор пройдет успешно, то получим алгебраический терм, который является семантикой программы x . Программа x является отображением их входных данных в выходные данные. Суперпозиция базисных функций программы x (алгебраический терм) является математической моделью данной программы x, а семантика языка программирования представляет собой универсальную алгебру A с сигнатурой операций О = Ф}е¥ . Таким образом, если L — это множество синтаксически правильных программ типа (текст), T(О) — множество суперпозиций базисных функций из О, ст — алгоритм синтаксического разбора, то ст : L ^ T(О)

взаимно однозначное отображение,

V x е L ст ( x ) е T ( О ) .

Из примитивов наиболее интересным и существенным является операция отождествления. Операцию отождествления для формальных грамматик впервые ввел Виталий Алексеевич Тузов [1; 2].

Пусть ф , / — слова в алфавите V N и V T (сентенциальные формы грамматики G ), где нетерминальные символы помечены индексами, которые являются формальными параметрами операции отождествления. Тогда операция отождествления синтаксически представляется в виде ( ф ) / и содержательно определяется как отображение совокупности входных формальных параметров, принадлежащих к ф , на совокупность выходных (т. е. результирующих) формальных параметров, входящих в / . Семантически операция отождествления ( ф ) / трактуется так: если

*

x — фактический аргумент этой операции, то строится вывод ф ^ x этого слова в грамматике G M . Тогда нетерминальные символы слова ф получают в качестве значений некоторые подслова слова x (одинаковые нетерминалы, помеченные одинаковыми символами, должны принимать одни и те же значения), слово / определяет результат этой операции [1].

Все операции начинаются с исходных данных (что дано). Любая операция имеет исходные данные и результат. Сказанное продемонстрируем на примере.

Пусть задана грамматика G = ( V N , V_T , P , A ) , где A е V N — начальный нетерминальный символ.

Обозначим за: ф — исходные данные, / — схема получения результата.

Синтаксически операция отождествления выглядит следующим образом:

( ф ) / ,    где ф , / е ( V n и V t ) .

Рассмотрим подробнее исходные данные операции отождествления на примере:

ф = N 1 T 1 N₂ т ₂ N₃ т ₃, где N i е V_N , T i е V T .

ф ^G x

будет обозначать вывод из сентенциональной строки ф е ( V N u V_T ) в строку x , состоящую из терминальных символов V_T , т. е. ( x e V_T * ). На рис. 1 вывод ф ^ G x будет иметь вид:

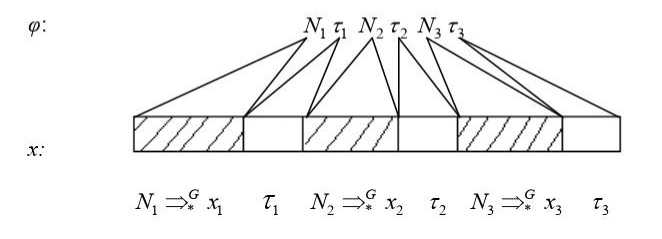
Рис. 1

На этой диаграмме x i ( i = 1,3) являются подстрокой строки x . Процесс вывода начинается слева направо по очереди: N 1 ^ G x 1 , затем тождественное отображение т 1 e V_T * переходит на остаток строки x справа от x 1 , затем N ₂ ^ G x ₂ и т. д. (рис. 1). Этот грамматический разбор является левым, т. к. разбор начинается слева направо и задает однозначность операции отождествления. В результате этого разбора (на данном этапе) нетерминалы получают следующие значения: N 1 = x 1 , N ₂ = x ₂, N ₃ = x ₃. Так как множество нетерминалов из ф содержит множество нетерминалов у , то у получают однозначное значение: N ( ф ) о N ( у ).

Вышеизложенное легко можно обобщить для m -го порядка:

у = t i N i ... t i    N i t i , где t i могут быть пустыми строками.

1 m - 1 mm j

{ N i , N 2 ,..., N m } 2 { N 1 , N i 2 ,

., N i }. m

ϕ

ψ

Областью определения операции отождествления является множество * G

О _ф = { x I x ^G V T , Ф > * x }.

Продемонстрируем на содержательном примере применение операции отождествления. Для этого рассмотрим фрагмент программы:

начало имя имя цел S, SQ ; \\ <описания> Ф2

S := 2; SQ := 1; \\   <операторы>

SQ := SQ + S \\                    У <программа> Ф1

конец.

Интуитивно понятно, что это отображение исходных данных на множество результативных данных Ф1:D ^ ^ D ^ ( D ^ — область определения, D ^ — область результативных значений).

Естественным было бы рассмотреть отображение всей программы Ф 1 как композицию функций. Поскольку синтаксис программы подчиняется синтаксическому правилу

<программа> : := начало <описания> ; <операторы> конец Ф1, которое разбивает программу на два раздела <описания> и <операторы>, то естественным было бы построить отдельную функцию для <описания> - Ф 2 и <операторы> - Ф 4. Тогда функция Ф 1 является композицией функцией Ф 2 и Ф 4 : Ф 1 = Ф 2 о Ф 4 (прим. композиция выполняется слева направо, обычно в математике Ф 1 = Ф 4( Ф 2 (исходные данные)).

Эту идею разбивки отображений и предложений в виде композиций более «мелких» функций можно рекурсивно продолжить по правилам синтаксической грамматики. Рассмотрим дерево грамматики (рис. 2).

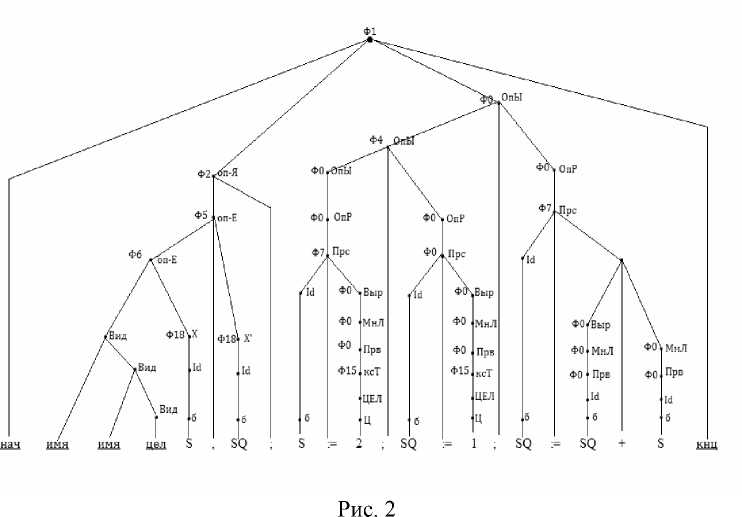
Заключение

Разработан подход к компьютерному моделированию динамических систем с помощью функциональных грамматик. Компьютерную программу удалось представить как суперпозицию базисных функций. В работе рассмотрена операция отождествления, которая является существенной при разработке моделирующих программ. Представлен фрагмент компьютерной программы, на которой выполнена операция отождествления и получен терм — суперпозиция базисных функций. Также построено дерево компьютерной программы, в узлах которой находятся базисные функции.