Моделирование динамики численности популяции кабарги с учетом половой структуры и промысла

e-mail: ,

Изучение закономерностей динамики численности животных является ключевой задачей для оценки ресурсного потенциала региона, рационального использования и охраны биологических ресурсов. Изменения в численности популяций обусловлены как внутренними биологическими характеристиками видов, так и внешними факторами среды. Для многих видов животных важно учитывать половую структуру. Половозрастная структура популяции существенно влияет на характер колебаний ее численности, поскольку особи разных возрастов и полов имеют различия в выживаемости и вкладе в воспроизводство [1]. В структурированных популяциях промысловому изъятию часто подвержены только особи определенного возрастного класса и пола. Для крупных млекопитающих, таких как копытные, промысел может непосредственно влиять на размер популяции, возрастной состав и половую структуру. Реакция популяции на изъятие и его прогноз могут быть осложнены из-за демографической структуры (различия в показателях естественного движения популяции в зависимости от возраста, размера или пола) и процессов, зависящих от плотности. Кроме того, изучение избирательного промысла по полу особенно актуально для видов, где самцы и самки различаются по поведению, морфологии или экономической ценности.

В предшествующей работе [4] на основе дискретной во времени математической модели с учетом полового состава популяции и с плотностным лимированием выживаемости молоди был проведен анализ динамики численности копытных, обитающих на территории Еврейской автономной области (ЕАО). При этом оценка демографических параметров популяций проведена на основе подхода, учитывающего только общую численность [4, 5]. Основная идея данного подхода заключается в переходе от двухкомпонентной модели динамики популяции с половой структу-

рой к разностному уравнению с запаздыванием, зависящему только от общей численности.

Данное исследование направлено на изучение динамики численности популяции кабарги Moschus moschiferus в ЕАО с учетом влияния промысловой нагрузки. Основным источником информации о численности охотничьих животных являются материалы годовых отчетов по зимним маршрутным учетам, проводимым государственными службами, отвечающими за охрану и использование объектов животного мира в ЕАО [2].

Для описания и анализа динамики численности структурированной популяции была применена дискретная во времени математическая модель с учетом полового состава популяции и с плотностным лимированием выживаемости моло- ди:

fn + 1 = a8 fn exP(-aNn ) + 5 fn mn + 1 = a(1 - 8)fn exp(-PN„ ) + v mn

где п – номер сезона размножения, f и m – численности самок и самцов соответственно, N = f + m – общая численность популяции, a – репродуктивный потенциал популяции в отсутствие лимитирующих факторов (среднее число потомков, приходящееся на одну самку), δ – доля самок среди новорожденных, s и v – коэффициенты выживаемости половозрелых самок и самцов соответственно.

Функции w 1 = exp( - a N_n ) и w 2 = exp( - p N_n ) определяют зависимость выживаемости неполовозрелых самок и самцов от общей численности популяции. При этом коэффициенты α и β характеризуют интенсивность снижения выживаемости неполовозрелых самок и самцов соответственно, которое вызвано конкурентным взаимодействием между особями. Параметры α и β связаны с емкостью экологической ниши популяции, включая влияние плотностно зависимых факторов (доступность пищи, конкуренция за ресурсы), хищников и антропогенных факторов (охота, пожары, вырубка лесов и др.), если они не моделируются явно.

Предполагается, что рассматриваемая популяция подвержена ежегодному промысловому воздействию с постоянной долей изъятия. Следовательно, модель (1) с учетом промысла самок и самцов примет вид:

f f n + 1 = ⁽ a ⁸ fn ^ex P ^{( -a N}n ) + ⁵ f„ ) ■ ⁽1 ^- u i ) (2) 1 m n + 1 = ⁽ a ^{(1 - 8} ) fn ^exp^{( - в N}n ) ⁺ v m n ) ■ ^{(1 -} u 2 )

где u ₁ и u ₂ – доли изъятия самок и самцов соответственно.

Равновесные значения численности самок и самцов, соответствующие координатам непод- вижных точек системы (2), определяются по сле- дующим формулам:

(1 - v (1 - u ₂) n

f

a

a 8 (1 - u 1 )

1 - 5 (1 - U 1 )

(          /             \ в / a

( a (1 - 4444 У

I a 8 (1 - U 1 ) J

V

-

v (1 - u 2 ) + 1

J

m = f ■

a (1 - 8 ) (1 - u 2 )

1 - 5 (1 - U 1 ) a 8 (1 - u ₁ )

в / a

1 - v (1 - u ₂ )

При этом равновесная численность всей популяции составляет N = f + m . Отметим, что при нулевых значениях u1 = 0 и u2 = 0 формулы (3) дают равновесные численности самок и самцов для системы (1), что соответствует условию отсутствия промысла.

В связи с отсутствием данных о половом составе охотничьих ресурсов ЕАО, целесообразно переписать модель (2), используя только общую численность [4]. Переход от раздельного учета численностей самок f и самцов m в модели (2) к агрегированной переменной – общей численности N – приводит к одномерному рекуррентному урав- нению с запаздыванием:

N n + 2 =

' ^{(1 - u} 1 ^{)( 5} + ^{a 8 e} “ N " ^{+ l)} + ^{(1 - u} 2 ^{)((1 -}

[ 1 +

₄- 8 ) a e ^e N^{n + 1}

- v

+___________ ( V - a (1 - 8 ) e - ^e N )(1 - u 2) ___________

(1 - u 1 ) ( 5 + a 8 e " N ) + (1 - u ₂)((1 - 8 ) a e ^e N - v )

X

^x ( ^Nn + 1 ^{- vN}n ^{(1 - u} 2 ) ) ⁺ v ^Nn + 1 ^{(1 - u} 2 )

Применение уравнения (4) позволяет по данным общей численности оценить параметры, характеризующие процессы воспроизводства и половую структуру, что может быть использовано для анализа и описания динамики численности природных популяций. Заметим, что если принять u ₁ = 0 и u ₂ = 0 в (4), то получим уравнение с запаздыванием для оценки параметров модели (1).

Для оценки адекватности соответствия модельных расчетов эмпирическим данным были рассчитаны скорректированные по числу степеней свободы коэффициенты детерминации ( R ² ) и средние ошибки аппроксимации ( A ).

Проиллюстрируем результаты оценки параметров моделей (1) и (2) с использованием уравнения (4) для популяции кабарги. На рис. представлена динамика учетной и модельной численности кабарги – по модели (1) в отсутствие промысла и по модели (2) с промысловым изъятием.

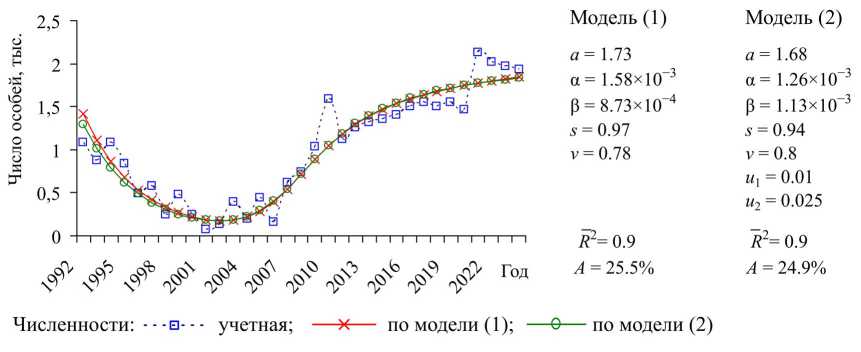
Рис. Учетная и модельная численности популяции кабарги в Еврейской автономной области при δ=0.5

Fig. Real and model data on the musk deer in the Jewish Autonomous region at δ=0.5

Согласно оценкам качества описания модель (4) (как с промыслом, так и без него) хорошо описывает временной ряд, соответствующий учетной численности кабарги. Большие значения скорректированных коэффициентов детерминации (0,9) отражают высокую коррелированность изменений учетных и модельных данных. Действительно, модельные траектории повторяют тенденцию снижения численности кабарги в период 1992–2001 гг., а затем, с 2002 г., – рост ее численности. Вместе с тем средняя ошибка аппроксимации показывает, что модельные траектории отклоняются от учетных данных на 24,9–25,5%. Наблюдаемые расхождения между модельными и фактическими данными, скорее всего, вызваны дополнительными факторами, не отраженными в модели и оказывающими влияние на динамику животных.

В соответствии с модельными оценками, численность популяции кабарги характеризуется устойчивым типом динамики, при котором наблюдаются ее медленные, растянутые во времени плавные подъемы и сокращения (рис.). Отметим, что кабарга, как и большинство видов копытных, относится к «равновесным» видам с К-стратегией [1], и их динамика представляет собой длиннопериодические устойчивые колебания с флуктуациями вокруг состояния равновесия (рис.). Заметим, что точки, соответствующие найденным оценкам коэффициентов модели (4) (как с промыслом, так и без него), находятся в области устойчивости систем (1) и (2). Следовательно, возникающие коле- бания численности по большей части обусловлены влиянием внешних факторов и представляют собой отклонения от состояния равновесия.

Согласно модельным расчетам (1) и (2), ожидается, что популяция кабарги достигнет равновесной численности в 2.1 и 1.99 тысячи особей соответственно. Модельный рост численности обеспечивается сравнительно высокими значениями репродуктивного потенциала (1,7 и 1,68) и высокими оценками коэффициента выживаемости взрослых самок (более 0,9). Доля изъятия самок, согласно оценкам, составляет менее 0,01, самцов – 0,025. По данным официальной промысловой статистики, ежегодный промысел кабарги составляет около 4%. При этом отстрел самок составляет около 10% от всего объема промысла [2].

Анализ равновесного состояния показывает, что доля самок кабарги составляет 61,6% в отсутствие промысла и возрастает до 71,5% при наличии охотничьего пресса. Следовательно, промысловая нагрузка, направленная преимущественно на самцов кабарги ( u ₁ = 0,01 и u ₂ = 0,025 по модели (2)), вызывает сдвиг равновесного полового состава популяции в сторону увеличения доли самок. Кроме того, повышенная доля самок в популяции в отсутствие промысла свидетельствует об интенсивном росте численности кабарги [3], что подтверждается данными мониторинга (рис.).

Отметим, что интенсивность экологического лимитирования самок (α = 1,58×10-3), оцениваемая по модели (4) в отсутствие промысла, почти в 2 раза превышает данный показатель для самцов (β = 8,73×10-4). При этом, если оценивать 4. эти показатели по модели (4) с учетом промысла, то данные параметры практически уравниваются, т.е. α = 1,58×10-3и β = 8,73×10-4. По-видимому, различие в значениях α и β может быть обусловлено избирательностью охоты на самцов. Действительно, если исключить влияние изъятия из коэффи- 5. циента выживаемости (смертности) самцов w2, то текущая численность популяции N, стоящая в показателе степени, уменьшится и, следовательно, в силу сохранения балансовых отношений коэффициент β увеличится. Это связано с тем, что смертность становится более зависимой от плотности, так как исчезает «внешний» источник гибели осо- 1. бей.

Таким образом, представленный в работе модельный подход демонстрирует возможность оценки половозрастных характеристик популяции и внешних факторов (уровня антропогенной на- 2. грузки) по агрегированным данным о численности. При этом обеспечивается относительно хорошее соответствие с учетными полевыми данными.

Работа выполнена в рамках государственного задания Института комплексного анализа региональных проблем ДВО РАН FWUG-2024-0005 (№ государственной регистрации 125011000074-3).