Моделирование динамики и балансировка гибкого ротора по N-й форме изгиба оси

Введение. Вследствие конечности изгибной жёсткости оси любого реального ротационного агрегата (ротора) машины он имеет бесконечное множество критических скоростей wKpi вращения, соответствующих каждой из / = 1, 2, ..., п, ... собственных форм изгиба его оси [1]. Там же обосновывается, что к гибким следует относить роторы, максимальная эксплуатационная скорость соэ которых отвечает условию соэ > 0,857(0^1. Гибкий ротор балансируется по л-й форме изгиба [2], если сокр(л1) < со3 < шкрп. При n = 1 солр(л1) = 0 и гибкий ротор балансируется по 1-й форме изгиба, если 0,857солр1 < со, < шкр1

У каждого реального ротора, сбалансированного на низкой скорости со5 « со^ по традиционной технологии динамической балансировки с коррекцией дисбалансов в двух плоскостях коррекции у опор, объективно наличие исходного неупругого искривления оси, названного в [1] линией эксцентриситетов масс ротора. Эта линия представляет собой пространственную кривую отклонений (эксцентриситетов) центров масс элементарных сечений ротора, перпендикулярных его оси, от оси его вращения (прямой, соединяющей центры опор). Эту кривую можно разложить по собственным формам исходного неупругого изгиба [3], каждая из которых лежит в некоторой плоскости, содержащей ось вращения ротора.

Вследствие исходного изгиба оси ротора по каждой из собственных форм дисбалансы от него распределяются неравномерно по этой форме. С приведением ротора во вращение со скоростью со > со_б усилия от этих дисбалансов ведут к упругой деформации оси по всем собственным формам её изгиба. Чем ближе со к ш_Кр» i= 1, 2, ..., n, ..., тем значительнее эта деформация по Ай собственной форме. При со = to_Kpj наступает резонанс по Ай форме изгиба.

Существующие методы балансировки гибких роторов (высокочастотная балансировка) не имеют общей теоретической основы. Учёт упругих изгибных деформаций оси гибкого ротора при его балансировке и в эксплуатации «крайне усложняет процесс балансировки и затрудняет установление общей методики балансировки, пригодной для гибких роторов любой категории» [3].

Представленные ниже решения позволяют устранить эти недостатки и создать общий алгоритмический подход к последовательной балансировке гибкого ротора по каждой из / = 1, 2,..., л собственных форм изгиба.

Моделирование динамики ротора, сбалансированного по / = 1, 2, ..., (л - 1)-й собственным формам. Объект исследования — двухопорный ротор в виде однородного гладкого кругового цилиндра с исходно изогнутой осью по всем собственным формам. Этот ротор предварительно сбалансирован динамически на низкой скорости вращения шб «: со t по традиционной технологии в двух плоскостях коррекции у опор. Кроме того, он последовательно сбалансирован по / = 1, 2,..., (л - 1)-й собственным формам по специальным методикам, о которых речь пойдёт ниже. Полагаем проведённые балансировки идеальными, поэтому вращение такого ротора со скоростью 0^,,^

\крп не вызовет дополнительных прогибов оси по / = 1, 2, ..., (л - 1)-й собственным формам, а вызовет лишь дополнительный прогиб оси по / = л-й собственной форме. Дополнительный упругий прогиб оси по более высоким формам изгиба при этом будет пренебрежимо малым.

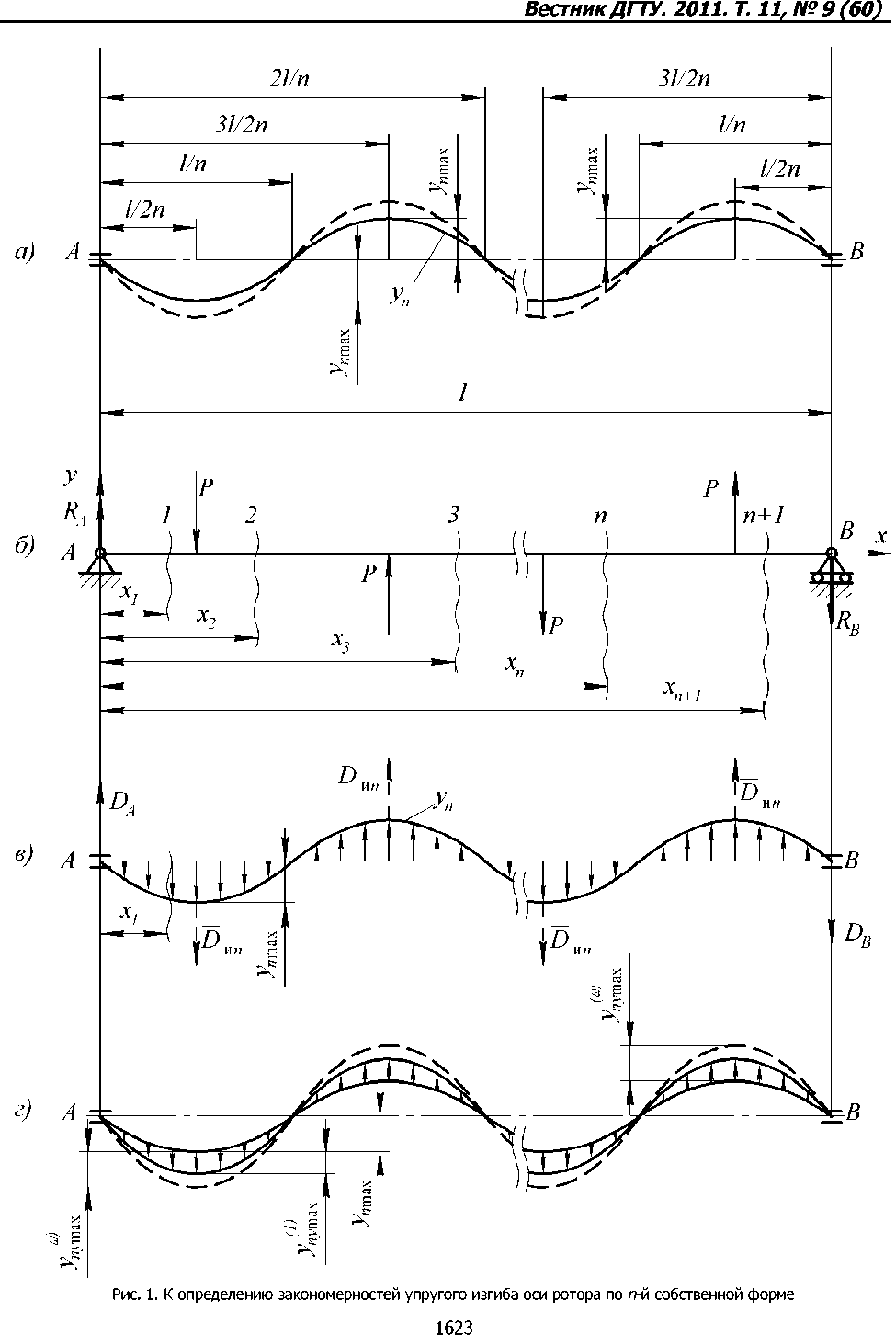
На рис. 1, а сплошной линией представлена схема исходного искривления оси ротора по / = л-й собственной форме, а пунктирной линией — её искривление по той же форме после при- ведения ротора во вращение со скоростью

Представим исходное искривление оси ротора по л-й собственной форме изгиба как результат её пластической деформации под действием чередующихся по направлению и равных по модулю сил Р, приложенных к ротору в л точках на его оси (см. рис. 1, б). Для описания этого искривления нашли реакции Р_А = 0,5/3 Р_в =(-1)”¹ 0,5а опор ротора от действия приложенных сил. Разбив балку на участки 1, 2, ..., л + 1, записали для каждого участка выражение для изгибающего момента и, использовав известный из [4] метод расчёта деформаций балок, получили общие уравнения смещений у_п поперечных сечений оси балки, изогнутой под действием приложенной к ней совокупности усилий Р.

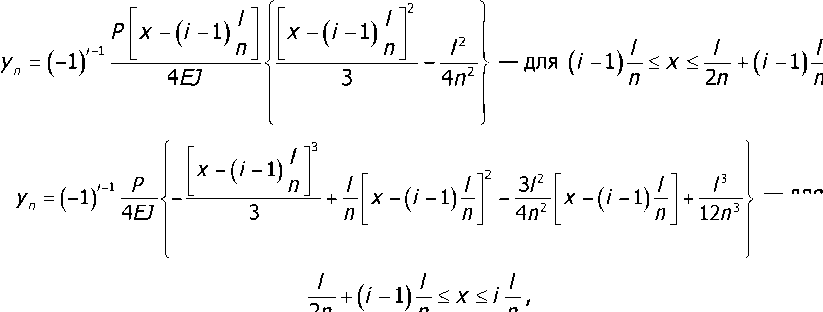
> — для

где / = 1...Л— номер участка балки, содержащего выпуклую или вогнутую волну л-й собственной формы изгиба оси; Е — модуль упругости материала упруго деформируемого вала ротора; J— момент инерции сечения вала ротора.

Экстремальное значение Уптах прогиба оси (стрелы прогиба) на каждой Ай волне л-й собственной формы изгиба оси ротора определили из (1) как у = У

⁷ л max ⁷ 1

2л ^v ' п

PI3

48EJn3 "

Из (2) нашли значение сил Р, которыми нагружена балка по схеме рис. 1, б, которое обеспечивает стрелу прогиба Уптах при л-й собственной форме изгиба этой балки:

/ 4857л3

' уЗ     Уптах ^е

Подставив модуль этой силы в (1), получили окончательные выражения для описания исходного неупругого искривления оси ротора по л-й собственной форме:

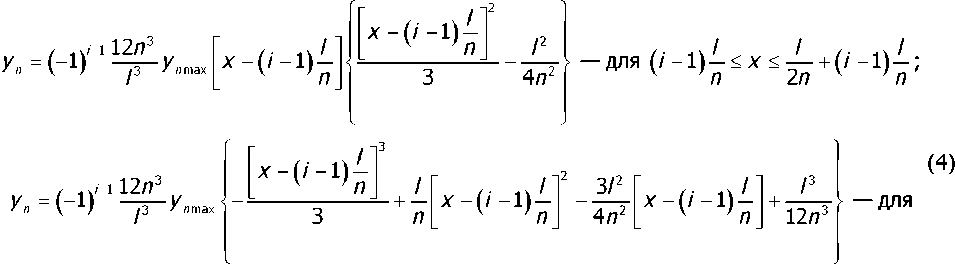
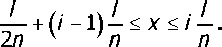
Построенная по этим уравнениям линия у_п исходного неупругого искривления оси ротора по /т-й собственной форме изгиба представлена сплошной линией на рис. 1, а. Такое искривление оси ротора приводит к возникновению на каждом из его участков длиной 1/п дисбалансов, распределённых с непостоянной интенсивностью:

dm(x) = moyndx.(5)

Используя последнее, нашли значение О_ил главного вектора дисбалансов, обусловленных исходным изгибом оси ротора на участке 1/п. Для этого подставили в (5) первое из уравнений (4) и после проведения интегрирования получили

—    //л —           //2л —5 т —

D™ = [ dnn (х) = 2m0 J yndx = -—уnmax.

о                  о° "

Приведение рассматриваемого ротора во вращение со скоростью щ^^ < со < со_хрл вызовет дополнительное (к исходному) упругое искривление его оси по /т-й собственной форме. Оно представлено пунктирной линией на рис. 1, а и вызвано действием лишь инерционных усилий от дисбалансов, распределённых по (5) и представленных на рис. 1, в. Найдём этот прогиб, оперируя значениями дисбалансов, а не инерционными усилиями, им пропорциональными.

Заменив на каждом участке 1/п распределённый дисбаланс эквивалентным ему главным вектором дисбалансов О_ил , определённым по (6), нашли реакции опор:

Da = 0,5D™, De = (-l)ⁿ⁺¹0,50»,.                          (7)

Выделив на левом участке сечение с координатой х^ (рис. 1, в), определили равнодействующий дисбаланс от распределённой нагрузки при 0 <  х < х_г —

Dxx = [ moyndx, о что после подстановки первого из уравнений (4) с / = 1 и проведения интегрирования позволило получить

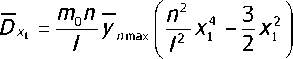
Координату плоскости приведения дисбаланса DXv определили как х Г х • v dx

О что после подстановки (4), (8) и проведения интегрирования дало

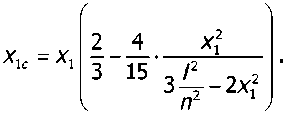
Изгибающий момент MuY в сечении Ai с учётом (7)...(9) привели к виду м m     (5     1 л2 з 1 л4

• ¹    и! - _п / лтах 1 £ 1 э /2 ^Л1 к /4 ^Л1 '                                 I¹ W

П       1^10      Z / Э / J

Дифференциальное уравнение упругой оси ротора на участке 0 <  x_Y< 1/2п имеет вид d^y со² m Г 5     1 л²₃ 1 л⁴

dx_Y D л^Ултах(1б ¹ 2 /^{2 1} 5 /⁴ J

Интегрируя дважды последнее уравнение с начальными условиями: х1=0^у=0,

I dy п               с                                                        „

-->—— = 0, в первом приближении получили уравнение упруго деформированной оси ро-2л dxY тора на участке 0 < xY < 1/2п от действия неуравновешенности, обусловленной исходным неупругим искривлением этой оси по л-й собственной форме, при приведении ротора во вращение со скоростью (О^,^ < со < шкрп -

/л

= Упу =

СО2 Л7 Г 61   /2       5 з 1 Л2 5    1 Л4 7)

Ёт" "л^^Тэго'л2"*19б%1 +40"гТо'К^1 /

(И)

На участке Ч2п Y< I/п упругий изгиб оси будет симметричным относительно точки x_Y = //2л, в которой имеет место экстремум упругого прогиба оси (рис. 1, г):

у⁽¹⁾ = а -у ,           а = 0,01^^-,                     (12)

/ путах п /птах*                п         D -п⁴ '                              '

где а_п — коэффициент упругого приращения стрелы прогиба оси ротора по л-й собственной форме изгиба при его вращении со скоростью со^^ < со <  ш_крп.

Последний результат получили подстановкой % = //2л в (11). Анализируя его, отметим, что значение а_п представляет собой не что иное, как аналитическое выражение квадрата отношения со/со_хря, так что

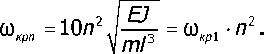
Поэтому для рассматриваемого ротора любая л-я критическая скорость больше первой критиче^ ской в л² раз, и поскольку со^^ < со <  ш_крп, то a_n < 1.

Как отмечено выше, уравнения (11), (12) позволяют лишь в первом приближении оценить дополнительный упругий прогиб оси ротора от исходного её искривления по л-й собственной форме со стрелой уятах^0 (рис. 1, а\ Найденные по этим уравнениям значения y™(xj и у^тах приводят к появлению новых распределённых неравномерно дисбалансов (показаны на рис. 1, г) дополнительно к дисбалансам от исходного неупругого искривления оси ротора по л-й собственной форме. Эти дополнительные дисбалансы ведут к новому дополнительному упругому прогибу оси ротора по л-й собственной форме и т. д. Учитывая это и используя формулу суммы членов бесконечно убывающей геометрической прогрессии, нашли стрелу прогиба оси ротора в установившемся его вращении со скоростью со:

1/       — V \ ' Я                                       1

У путах У птах / , п ₁                                                                v

Заметим, что при ал -> 1 стрела дополнительного упругого прогиба оси нежёсткого ротора по /т-й собственной форме у^^ах ^00 ■ ПРИ отсутствии исходного неупругого искривления оси ротора по п-й собственной форме (ултах=0) расчёт по (14) даёт у^ах=° ПРИ ап <1- ПРИ ап =1 тот же случай приводит к неопределённости, отражающей неустойчивое состояние ротора, когда бесконечно малое значение ултах приводит к неограниченному росту у^^ах, характерному для резонансного режима.

Поскольку упругий и исходный (неупругий) прогибы оси ротора по каждой п-й собственной форме (п = 1, 2, ...) лежат в одной осевой плоскости, суммарная стрела прогиба оси по п-й собственной форме определится как

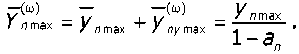
При а_П >1 расчёт по (14) даёт у^_ах<0 и (15) приводит к ^ <У„_тах ■ Это согласуется с теорией колебаний валов, констатирующей уменьшение неупругой деформации валов при их вращении со скоростями выше критических. Однако при пуске машины переход со = ш_крп может привести к негативным для всей конструкции машины последствиям и потому недопустим без проведения балансировки по п-й собственной форме.

Для жёстких роторов а_П = 0, и потому для них у^_ах = 0 и У^_ах = у_птах.

Механико-математическая модель неуравновешенности ротора, балансируемого по п> 1-й собственной форме изгиба. На каждом участке ротора, имеющем длину 1/п , деформации оси на скорости со будут приводить к возникновению результирующего локального вектора D™ распределённых неравномерно дисбалансов (рис. 1, г), определяемого с помощью (6) как

—(«>) 5 т —м   5 т у гу —    111 v —         * птах

L/ ип — ~ ---/ п max — ~    - ------

8 п 8 п 1-а„ где Ултах определено по (15), а ап < 1 по (12). Приложен D™ в центре каждого рассматриваемо'

го участка ротора длиной 1/п (аналогично тому, как приложены векторы О_ип на рис. 1, в).

Приведём всю совокупность определённых по (16) результирующих дисбалансов D™ к —(ю)                              ( главному вектору Dem и главному моменту Моп дисбалансов ротора в целом, имеющих место при вращении его со скоростью щ^^ < со < шкрп:

дИ_1-(-1)дИ        мН 1-(-1) пИ J(17)

L/cm —---------L/ип ,             1*1 Dn —-----~L/ип

• 2                              22

При принятой на рис. 1 системе отсчёта деформаций оси ротора, когда на первом слева участке оси протяжённостью 1/п имеет место у<0, D™ будет всегда направлен в сторону у_лтах на этом участке и приложен в центре пролета / между опорами ротора. При этом De™ ^0 и ---(ш)

Моп =0 будет иметь место лишь для нечётных номеров л собственных форм изгиба оси ротора. Главный момент Моп дисбалансов ротора будет иметь место лишь для чётных значении п при

D^{^n = 0. Этот момент лежит в плоскости исходной деформации оси ротора по чётной л-й собственной форме изгиба и при принятой и оговорённой выше системе отсчёта этих деформаций он будет направлен против часовой стрелки. При отсутствии исходного искривления оси ротора по л-й собственной форме стрела такого искривления на участке //л оси ротора у_лтах =0, и значения D^, М^п обращаются в ноль при любом со_хр(л1)< ш <  ш_крп.

Если рассматриваемый ротор при ултах * 0 привести во вращение со скоростью оо на ба лансировочном станке, то измерительная система станка зафиксирует в плоскостях коррекции 1,

—(ш)   —(ш)

2 необходимость установки в них корректирующих дисбалансов Ош, /7^2, параллельных при нечётном и антипараллельных при чётном л:

0,5/ - С Моп

Uknl — —1-/стп--- в в

-и _ -н о,5/-л Моп

Ukn2 — ~ U стп --1--

В в

где Д С— расстояния от опор ротора до ближайших плоскостей коррекции; В— расстояние между плоскостями коррекции; /= А + В+ С.

Уравнения (17), (18) и соотношения (12), (16), раскрывающие входящие в них величины, представляют собой механико-математическую модель неуравновешенности ротора, балансируемого по (л > 1)-й собственной форме изгиба. Входом этой модели является варьируемое значение сохр(л_1) < со < шкрп. Собственные свойства модели характеризуются значением и углом стрелы ултах исходного искривления оси ротора по л-й собственной форме изгиба, а также параметрами л?, Е, J, I, А, В, С конструкции ротора, определяющими по (12) комплексную характеристику ап и входящими в (18). Выходы модели — характеристики неуравновешенности ротора (Z7™, D^, M^n, D^k, D^V), определяемые по (16)...(18) при любом сохр(л1) < со < шкрп.

Идентификация параметров механико-математических моделей неуравновешенности роторов и их балансировка. Практическое использование построенной модели неуравновешенности для решения задач балансировки ротационных агрегатов машин при их проектировании, производстве, эксплуатации, ремонте требует знания всех характеристик и параметров соб ственных свойств. К ним относятся отмеченные выше у/тах — стрелы исходного неупругого прогиба оси ротора по / = 1, 2,..., л,... собственным формам изгиба, а также значения m, Е, J, I, А, В, С. Все эти характеристики для полного множества ротационных агрегатов каждого наименования являются случайными величинами с различными уровнями рассеивания их значений.

На проектной стадии создания ротационного агрегата конструктор имеет дело с оценочными (практически предельными, наиболее вероятными) значениями характеристик и параметров собственных свойств объекта моделирования, что позволяет прогнозировать с помощью модели неуравновешенное состояние ротационного агрегата на работающей машине и обеспечивать тем самым принятие обоснованных решений по его балансировке. Поэтому все параметры модели неуравновешенности проектируемого ротационного агрегата могут быть с той или иной достоверностью определены по различного рода справочным источникам. При этом в расчётах должны приниматься такие их значения, которые обеспечивают прогнозирование практически предельного возможного неуравновешенного состояния проектируемого ротора.

Использование модели неуравновешенности для проведения балансировки конкретного типоразмера ротора требует знания точных значений всех параметров и характеристик собственных свойств модели каждого балансируемого экземпляра ротора. Если этот типоразмер ротора необходимо балансировать по / = л-й собственной форме, то он должен проходить балансировку последовательно по / = 1, 2,..., л-й собственным формам. При этом для каждой из форм должна быть построена модель неуравновешенности с точными значениями всех параметров и характеристик собственных свойств.

Выражение для ап по (12) можно представить как a„=3„-w2; ^„=0,01-^ = ^

EJ-rr гг получив выражение для комплексной характеристики ₽„ собственных свойств модели неуравновешенности ротора, балансируемого на любой л-й собственной форме. По своему физическому смыслу р„ — величина обратная квадрату шкрп по (13). Эта характеристика определяется параметрами т, I, Е, J модели, о которых речь велась выше. При балансировке ротора по любой соб- ственной форме точному определению должны подвергаться значения ултах и ₽„, т. к. именно эти характеристики и определяют выходы модели по (16)...(19) как функции со.

Балансировка по 1-й собственной форме изгиба требует проведения низкочастотной балансировки на скорости со5 « covl, что предопределяет специфику балансировки роторов по этой форме, теоретически обоснованную и практически апробированную [1]. Там же представлена методика идентификации значения Pi, входящего в (19).

С решением последней задачи и расчётом р„ по последнему уравнению, идентификации подлежит лишь параметр ултах — стрела исходного искривления оси ротора по л-й собственной форме изгиба (рис. 1, а).

Приводя ротор во вращение на балансировочном станке со скоростью щ^^ <ш<ш_крп, будем иметь зафиксированными измерительной системой станка значения и углы корректирующих дисбалансов Dm, Dm в плоскостях коррекции у опор ротора. Для нечётных значений л >1 эти дисбалансы будут параллельными, для чётных — антипараллельными.

Имея определёнными эти дисбалансы, исходя из (17), (18), получили общее выражение для значения D^ результирующего вектора ^™ распределённых неравномерно на участке //л дисбалансов ротора

^ип - ^^Л1 ^ukn1 /2^2   /

Последнее с помощью (16) позволяет идентифицировать значение параметра ултах как

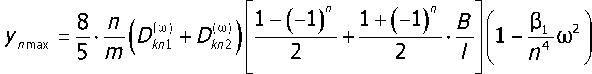
Угол у„1 вектора у_ятах на первой волне в системе координат, связанной с ротором, определяется как у_л1 =ф₁ +п, где ф_т — зафиксированный балансировочным станком угол корректирующего дисбаланса Dm .

Последующая балансировка ротора по каждой из / = 2, 3,..., л форм изгиба сводится к установке во всех л точках экстремума изгиба его оси корректирующих дисбалансов D_o = -О_ип , определённых по (6).

Заключение. Для ротора, имеющего < со₃<  ш_крп и потому требующего последовательной балансировки по / = 1, 2, ..., л-й собственным формам изгиба оси, все параметры его механикоматематических моделей неуравновешенности при балансировке по каждой собственной форме 1628

определяются по представленным выше соотношениям. Эти модели могут успешно использоваться для решения задач балансировки как при проектировании роторов, так и в их производстве и эксплуатации.