Моделирование динамики температурного поля в нестационарном приближении при выращивании монокристаллов методом Чохральского

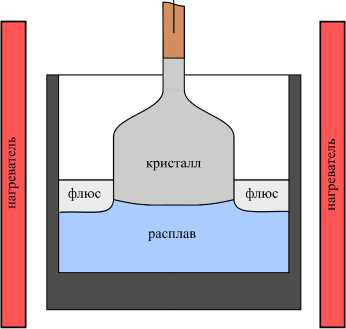
В работе рассматривается получение полупроводниковых монокристаллов методом Чохральского с жидкостной герметизацией расплава. Этот процесс является одним из вариантов направленной кристаллизации и состоит в следующем. Тигель, заполненный расплавом кристаллизующегося материала, находится в печи. Свободная поверхность расплава покрыта флюсом, который препятствует испарению компонентов из жидкой фазы. На начальной стадии в контакт со свободной поверхностью расплава приводится кристалл малого радиуса — затравка. После контролируемого расплавления ее небольшого объема инициируется процесс кристаллизации (Рис. 1а ). Образующийся монокристалл медленно достается из жидкой фазы. За счет изменения скорости вытягивания и температуры теплового узла радиус кристалла увеличивается до номинального. На развитой стадии процесса в ростовой камере поддерживаются условия, обеспечивающие рост кристалла постоянного радиуса (Рис. 1б ). Наиболее широко метод Чохральского с жидкостной герметизацией расплава применяется при производстве полупроводниковых монокристаллов арсенида галлия, использующихся в приборостроении.

Рис. 1. Модельная система: начальная стадия процесса ( a ); развитая стадия ( б )

( б )

Важнейшие параметры, характеризующие качество полупроводникового монокристалла — это однородность его состава, низкая плотность дислокаций, отсутствие дефектов. Основными источниками дислокаций служат температурные напряжения, возникающие в кристалле в ходе роста. Для повышения качества материалов необходимо осуществлять строгий контроль условий выращивания. Экспериментальная оптимизация технологических параметров является дорогостоящей и требует значительных временных затрат. Сократить число экспериментов в задачах кристаллизации позволяет математическое моделирование [1 –4] .

Форма растущего кристалла обуславливается сложным взаимодействием поверхностных процессов, протекающих на межфазных границах, а также тепло- и массопереносом внутри фаз. Уменьшение объема расплава при выращивании существенным образом сказывается на переносе энергии в системе. Для получения кристаллов постоянного радиуса на протяжении всего впроцесса необходимо динамически управлять температурой внутри ростовой камеры, что значительно усложняет подбор оптимальных параметров технологического режима.

Наиболее широкое распространение нашли математические модели, в которых не учитывается связь между формой боковой поверхности кристалла и полем температуры и предполагается, что радиус кристалла постоянен. В последние годы в рамках такого подхода достигнут ряд важных результатов. В работах [5 –10] изучена структура и характер течения в расплаве. Численный анализ влияния магнитного поля на перенос в ростовой камере проводился в [11 –16] . Связь формы фронта кристаллизации и напряжения с внешними факторами рассматривалась в [16 –23] . Модели, включающие изменение радиуса кристалла при его росте, обсуждались в работах [24 –29] .

Характерные времена физических процессов в ростовой камере (конвекции в расплаве, переноса энергии и массы внутри фаз, поверхностных явлений) существенно различны, а в целом длительность технологического процесса велика. Вследствие этого численное изучение технологии получения объемных монокристаллов на основе трехмерных моделей, учитывающих теплоперенос в печи, расплаве, кристалле и флюсе, естественную и вынужденную конвекцию в жидкой фазе, движение границ кристалл/расплав и флюс/расплав, изменение формы боковой поверхности кристалле, требует проведения многочасовых расчетов на современной вычислительной технике. Поэтому до сих пор не потерял актуальность анализ технологических режимов в рамках упрощенных осесимметричных моделей. Он дает возможность получать важные с практической точки зрения сведения при относительно небольших затратах машинного времени.

Целью данной работы является описание алгоритма, позволяющего определять форму боковой поверхности кристалла по мере его роста. Алгоритм основан на математической модели, учитывающей теплоперенос в системе тигель–кристалл–расплав–флюс, образование мениска у боковой поверхности кристалла, движение фронта кристаллизации, изменение радиуса кристалла [25] . На этапе разработки и тестирования предлагаемого метода конвективное движение в расплаве исключается из рассмотрения. Безразмерный анализ задачи показывает, что для кристаллов GaAs число Прандтля и характерные значения чисел Марангони и Грасгофа, соответсвенно, равны:

Pr = V П ~ 0.07, ^Ma = - о т R^T ~ 3^0 5 ^6-10 5 , Gr= RfiT ^Tg - 3.5Л0 7 ^7-10 7 . k^l/ ( c p p^l ) vk l /c p v ²

Здесь AT = 15^30 К — характерный перепад температуры между фронтом кристаллизации и боковой стенкой тигля (см., например, [30, 31] ); от = до/дТ = -1.2 г / ( с ² • К ), v = 0.005 см ² / с — кинематическая вязкость; в _т = 18 • 10 -5 К ^{- 1} — коэффициент температурного расширения. Значения остальных физических параметров приведены в таблице 1. Из экспериментов известно, что флюс, вязкость которого на три порядка выше вязкости расплава, стабилизирует движение жидкой фазы [32, 33] . Результаты прямого численного моделирования [9, 31, 34] свидетельствуют, что в рассматриваемом диапазоне параметров капиллярное течение имеет низкую скорость и практически не влияет на теплоперенос в системе. Анализ устойчивости движения жидкости, представленный в работах [7, 30] , показывает, что при Gr ~ 5 • 10 7 в расплаве наблюдается интенсивная тепловая конвекция, приводящая к значительному искривлению фронта кристаллизации. Таким образом, допущение об отсутствии естественной конвекции в расплаве, принятое в данной работе, справедливо лишь в условиях пониженной гравитации и в специальных случаях, когда для управления ростом кристалла применяется магнитное поле [35] . Вместе с тем надежность и гибкость предлагаемого алгоритма позволяют использовать его при более сложных моделях, учитывающих движение жидкости и капиллярные процессы на свободной поверхности расплава.

В основе обсуждаемого численного метода лежит геометрически консервативная разностная схема, гарантирующая выполнение законов сохранения массы и внутренней энергии. Для решения сеточных уравнений предложен специальный алгоритм расщепления по физическим процессам. Разработанный подход обеспечивает согласованный с законами сохранения расчет изменения положения фронта кристаллизации, боковой границы кристалла и мениска.

• 2.    Постановка задачи

2.1. Основные уравнения и граничные условия

Математическое моделирование нестационарного процесса выращивания кристалла строится в предположении, что перенос тепла в ростовой установке осуществляется механизмами теплопроводности и излучения, конвективное движение расплава не учитывается. Поле температуры является осесимметричным. Расчет ведется в области, расположенной в плоскости (r, z) и состоящей из четырех подобластей (Рис. 2) : тигля Щг, z) = {(r, z) : r е [0, R _c ], z е [Z o ,Z i } ; расплава ^ i (t,r,z) = {(r, z) : r G [0,R _c ],z e [Z i , Z 2 (t, r)]} ,

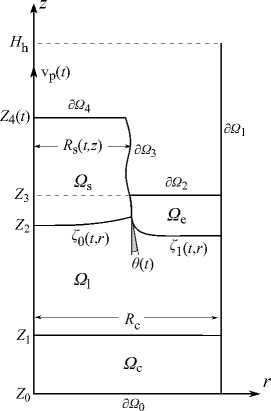
Рис. 2. Схема физической области задачи: Ωc – тигель, Ωl – расплав, Ωe – флюс, Ωs – кристалл где t — время; флюса ^e(t, r, z) = {(r, z) : r € [Rs(t, z), Rc], z € [Z2(t, r), Z3(t), ]} и кристалла ^s(t,r,z) = {(r,z): r € [0,Rs(t,z)],z € [Z2(t,r),Z4(t),]}. В задаче присутствуют три подвижные границы: боковая поверхность кристалла, заданная уравнением r = Rs(t,z); фронт кристаллизации z = Z0(t,r); граница между расплавом и флюсом — мениск z = Z1(t,r). Точка, в которой сходятся кривые r — Rs(t,z) = 0, z — Z0(t,r) = 0 и z — Z1(t,r) = 0, называется тройной. Угол, образующийся при контакте кристалла со смачивающим его расплавом, равен d(t). Вытягивание кристалла из расплава осуществляется со скоростью vp(t). Физические параметры задачи приведены в таблице 1.

Таблица 1. Физические параметры задачи

Параметр, единица измерения	Подобласть	Обозначение	Значение
	Ω c	c ρ	1.75
Плотность, г/см 3	Ω l	l ρ	5.7
	Ω e	ρ e	2.2
	Ω s	s ρ	5.2
	Ω c	c c p	1.05
Удельная теплоемкость, Дж/(г · К)	Ω l	c l ep	0.42
	Ω e	c p	1.8
	Ω s	c sp	0.42
	Ω c	k c	0.32
Коэффициент теплопроводности, Вт/(см · К)	Ω l Ω e	k l k e	0.14 0.02
	Ω s	k s	0.07
Степень черноты	Ω e	e ε	0.5
	Ω s	s ε	0.5
Температура плавления, К	-	T ph	1511
Скрытая теплота плавления, Дж/г	-	λ	720
Коэффициент поверхностного натяжения, г/c 2	-	σ	700
Равновесный контактный угол, град	-	θ eq	15
Радиус тигля, см	-	R cr	7.5
Высота тигля, см	-	H h	15
Скорость вытягивания, см/ч	-	v p (t)	0.5

Математическая модель процесса кристаллизации записана далее в безразмерном виде. В качестве масштаба температуры выбрана температура плавления T ph , пространственный масштаб определяется радиусом тигля R c , масштаб времени — t s _K = R 2 / (k s / (c p p s )) . Значения коэффициентов теплопроводности, плотности и удельной теплоемкости отнесены к соответствующим значениям твердой фазы, то есть k ^Y = k ^Y /k s , p ^Y = p ^Y /p s , c ^Y = c ^Y /c p , где индекс y принимает значения s,c,l,e . Безразмерные параметры, характеризующие кристаллизацию материала GaAs, содержит таблица 2, где σ ^∗ — постоянная Стефана–Больцмана, g — ускорение свободного падения.

Таблица 2. Безразмерные характеристики

Характеристика	Определяющая формула	Физический смысл	Значение
Число Пекле (вытяжка)	Pe = V p R cCp p s /k s	Перенос тепла за счет движения Теплопроводность	0.1
Число Стефана	St = A/(c p p s T ph )	Скрытая теплота плавления Количество теплоты	1.1
Радиационное число Био	Rad Y = ст * e Y R c T ph /k s , y = s,e	Радиационный теплообмен Теплопроводность	1
Число Бонда	Bo = gR 2 ( p - р е )/ст	Сила тяжести Сила поверхностного натяжения	290

Теплопередача в тигле, расплаве и флюсе описывается уравнением теплопроводности:

Y Y dT = 1[ £ ^ρ ∂t r ∂r

'rkY ^ +    ^

∂r ∂z     ∂z

,

(r,z) G ^ Y ( y = e,l,c).                      (1)

Перенос энергии в кристалле, движущемся со скоростью v p , задается уравнением:

СР ^ +Pe ^d T = 1Г » ∂t ∂z r ∂r

∂T    ∂    ∂T rk ]+ъ~ \гк

∂r    ∂z     ∂z

, (r,z) G ^s.

Тигель и расплав, расплав и флюс, а также флюс и кристалл находятся в идеальном тепловом контакте.

Из симметрии задачи следует, что dT/drlr=0 = 0.                                            (3)

Дно тигля теплоизолировано:

- k ^с дт/дп 1 _дП о =0.

Температура боковой стенки тигля изменяется по закону:

T U = T c ( t ) .

Предполагается, что флюс является непрозрачным. Радиационный теплообмен между боковой стенкой тигля ∂Ω 1 , поверхностью флюса ∂Ω ₂ и поверхностью кристалла ∂Ω ₃ ∪ ∂Ω ₄ определяется соотношениями:

e ∂T k _∂z

Rd.T 4 - T eq ) | _e „ 2 , ∂Ω 2

dT k ^s

∂n

= Rad(T4 -Tp‘)L     ,, .

^eq ∂Ω 3 ∪ ∂Ω 4 ∂Ω 3 ∪ ∂Ω 4

Здесь T eq — эффективная температура поверхностей , у частвующих в теплообмене, рассчитанная на основе угловых коэффициентов излучения F an _a - dn _e , а,в = 1,4 . Формулы для вычисления F dn _a - dn _e представлены в работе [36] .

• 2.2.    Условия на фронте кристаллизации

• 2.3.    Мениск

Температура на фронте кристаллизации равна температуре плавления. В безразмерном виде получим

T ( t,r,Z o ( t,r )) = 1 .                                                   (6)

Из закона сохранения внутренней энергии следует условие Стефана:

k l (dT/dn) | z=z 0 (r)— - k ^s (dT/dn)| z=Z o (r)+ = St[v p (t)-dZ o /dt]( n^ z ).                     (7)

Здесь v g (t) = v _p (t) - dZ 0 /dt — отклонение скорости фронта кристаллизации от скорости вытягивания; n — вектор внешней нормали к фронту кристаллизации; e z — единичный орт, сонаправленный с осью Oz .

Свободная поверхность жидкости вблизи границы расплав–кристалл искривляется и образует мениск. Средняя кривизна мениска, поверхностное натяжение жидкости и сила тяжести связаны уравнением Юнга–Лапласа для капиллярного давления: [25, 37] :

Z1 (t,r) = —f —+ — 1

Z1( ,) Bo ^1  R2J, здесь R1 и R2 — главные радиусы кривизны мениска:

1           dZ 1 /dr          1         d²Z 1 /dr 2

Rh = r[1 + (dZ i /dr) 2 ] ^1/2 , R = [1 + (dZ i /dr) ² ] ^3/2 .

Граничные условия для уравнения (8) имеют вид:

Z i (t,R) = Z o ( t,R )

dZ i /dr l r=i = 0,

где R — радиус тройной точки.

• 2.4.    Изменение радиуса кристалла

Для определения радиуса тройной точки R используется условие, предложенное в работах [24, 25, 38] :

∂R ∂t

^V P ^{( t )} - ddt ^tg[ ^ ^{( t )} -^ eq ].

Здесь θ eq — равновесный угол смачивания. Из (10) следует, что при θ>θ eq радиус тройной точки увеличивается, а при θ < θ _eq радиус уменьшается. Так как после затвердевания радиус точки, лежащей на поверхности кристалла, остается неизменным, форма боковой поверхности R s ( t,z) может быть найдена из уравнения переноса:

∂R s       ∂R s

-дТ+vp(t) 97=0, дополненного соответствующим граничным условием (10).

• 2.5.    Изменение объема расплава

Верхний торец кристалла движется со скоростью вытягивания

∂Z 4

at = ^{V p ( t ) .}

Из закона сохранения массы кристаллизующегося вещества d (plvl+psV s)=0

следует уравнение, описывающее изменение объема расплава с течением времени:

' ^V = -4 ! [V p (t)- dZ o /dt] ( n • e z ) dY.                                (13)

dt      ρ ^l

ζ 0 (t,r)

Таким образом, условия (6) – (13) полностью определяют динамику тройной точки и движущихся границ.

• 3.    Метод решения

  • 3.1.    Преобразование системы координат

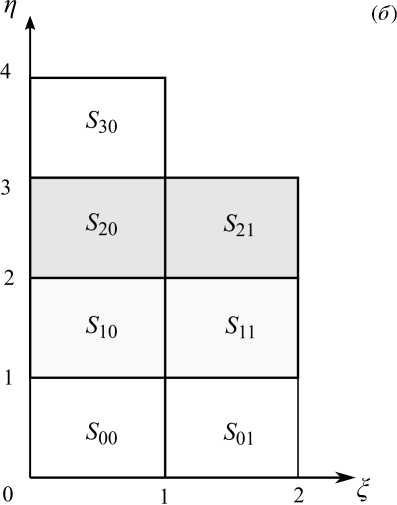
Основу метода решения задачи (1) – (13) составляет нестационарное преобразование системы координат [39] : физическая область Q(t,r,z ) отображается в расчетную область Q(t£,n ) (см. Рис. 3) . В новой системе положение границ z = Z _a ( t,r ) , где а = 0,4 , зафиксировано и совпадает с координатными линиями п = а , а границы

R o ( t,z) = O ,  R i (t,z) = |

R, zo(t,R)

R s ( t,z ) z>C ₀ ( t,R),

R 2 ( t,z ) = 1 ,

соответственно, переходят в прямые ( = 0, С = 1, С = 2 . Подобласти Q _a e в новой системе координат (см. Рис. 3б ) становятся прямоугольниками S _a e , а = 0,3, в = 0,1.

В общем случае системы координат (t,r,z) и (t,C,n) связаны выражениями:

t = t,   ^r = х^&п ) ,  z = Ф^п ) .

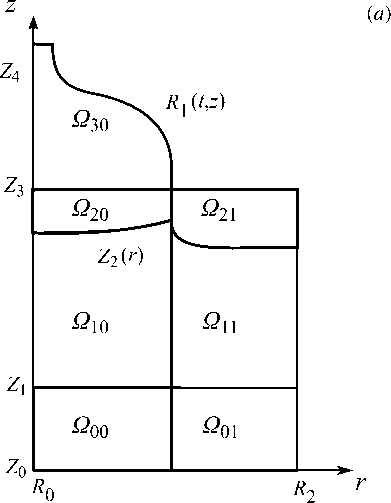
Рис. 3. Преобразование системы координат: физическая область ( a ); расчетная область ( б )

При наличии в физической области твердой и жидкой фаз преобразование (14) является невырожденным, и якобиан J = d ( t,r,z ) /d ( t,e,n ) = r ^ ^z _n — r _n z ^ не равен нулю.

• 3.2.    Основные уравнения в расчетной системе координат

Уравнение теплопроводности в расплаве, тигле и флюсе (1) в расчетной системе координат принимает вид [40, 41] :

' d ( rJT ) _ d ( rUT ) _ d ( rVT ) '

_ di        de dn _

∂ ξξ ∂T ξη ∂T ∂ ae de + dn + dn

(^nt 5T j^nn ^dT A v de + dn '

Здесь U и V — контравариантные скорости: U = r _t z _n — z _t r _n , V = r _t z ^ — z _t r ^ . Коэффициенты К ^, K € ⁿ , к nt , к ⁿⁿ из (15) вычисляются следующим образом: К^ = kr ( r ^ + z n ) / J, Кⁿⁿ = kr ( r 2 + z ^ ) / J, К ^ ⁿ = K ⁿ ^ = — kr ( r ^ r _n + z ^ z _n ) /J. Аналогичным образом преобразуются уравнение теплопроводности в кристалле (2) и граничные условия (3) – (5) . Условие Стефана (7) в расчетной системе координат становится следующим:

K - dT +K ⁿⁿ др)      — K n dT + к ⁿⁿ др      = Strr _e [v p (t) — dZ o /dt].

^{de      d}nJ n=2 - o V ^{de      d} nJ n=2+o

Якобиан преобразования системы координат и контравариантные скорости не являются независимыми величинами и связаны уравнением:

d ( rJ ) d ( rU ) d ( rV ) dt     de ⁺ dn

выражающим закон изменения площади в физической системе координат.

• 3.3.    Приближенное выражение формы мениска

Решение уравнения Лапласа для капиллярного давления (8) , записанного в расчетной системе координат, является отдельной трудоемкой задачей. Поэтому в данной работе для определения формы мениска используются приближенные аналитические выражения, полученные в [42] из уравнения (8) . Соответствующие формулы связывают высоту мениска h , радиус тройной точки R и величину контактного угла θ :

h = УвО(Т— cosa) + (Bo sina/4R) ² — Bosina/4R, a = n/2 — 0,                 (17)

а также форму мениска z = Z 1 ( t,r ) , радиус тройной точки и контактный угол:

r = f men ( z,R ( t),0 ( t)).                                              (18)

Конкретное выражение для f men опущено в силу его громоздкости (см. [42] , формула (18)).

При заданных h и R контактный угол может быть вычислен из уравнения (17) . Форма мениска, соответствующая полученным параметрам, определяется выражением (18) . В работе [42] показано, что в диапазоне физических параметров, характерном для материала GaAs и исследуемого технологического процесса, результаты, рассчитанные по приближенным формулам (17) , (18) , хорошо согласуются с численным решением уравнения (8) .

Уравнения (10) – (12) , представляющие изменение положения боковой границы и верхнего торца кристалла, рассматриваются в физической системе координат ( t,r,z ) .

• 3.4.    Разностная схема

• 3.5.    Вычислительный алгоритм

Разностная схема для уравнений, описывающих теплообмен в расчетной системе координат (t£,n ) , получена с помощью метода конечных объемов на неподвижной прямоугольной сетке. Подробное описание техники построения разностной схемы для моделирования роста кристаллов постоянного радиуса содержится в работе [43] . Консервативная разностная схема для задачи Стефана в области с искривленной боковой границей в декартовой системе координат предложена в работе [44] . Полученные здесь разностные алгоритмы в данной работе обобщаются на случай динамического учета изменения радиуса растущего кристалла. В кратком изложении характерные особенности используемого алгоритма расчета заключаются в следующем.

При аппроксимации производной по времени в уравнении теплопроводности (15) якобиан преобразования J = r ^ z _n — r _n z c и контравариантные скорости U = r _t z _n — z _t r _n , V = r t z ^ — z t rz вычисляются таким образом, чтобы они удовлетворяли дискретному аналогу закона сохранения площади (16) . Нарушение этого условия приводит к возникновению в аппроксимации уравнения (15) схемных источников/стоков внутренней энергии, пропорциональных шагу интегрирования по времени [45, 46] . При расчете длительных режимов выращивания искусственный источник/сток тепла может существенно исказить динамику процесса. В работе [44] из закона изменения площади контрольного объема в физической области получены явные выражения для вычисления J , U и V , тождественно удовлетворяющие неявной аппроксимации уравнения переноса якобиана в декартовой системе координат. При построении формул применялось дискретное преобразование системы координат. После проведения аналогичных несложных, но громоздких выкладок удается построить выражения отыскания J , U , V в цилиндрической системе координат, удовлетворяющие полностью неявной аппроксимации уравнения (16) .

Аппроксимация диссипативных членов в уравнении (15) производится с помощью самосопряженного, отрицательно определенного разностного оператора, рассмотренного в работах [43, 44, 47] .

Аппроксимации условий на границе раздела фаз и границах области согласованы с аппроксимациями соответствующих уравнений во внутренних узлах сетки, поэтому на разностном уровне выполнен закон сохранения внутренней энергии. В расчетах используется неявная разностная схема 2-го порядка точности по пространству и 1-го порядка точности по времени.

Алгоритм решения системы нелинейных сеточных уравнений, полученной при аппроксимации задачи (1) – (13) в расчетной системе координат, основан на специальной схеме расщепления по физическим процессам. Предложенный итерационный процесс может быть использован независимо от нахождения температурных полей внутри ростовой камеры.

На каждом шаге по времени t = t k сначала проводится расчет теплопереноса в системе тигель-флюс-расплав-кристалл. Моделирование теплообмена осуществляется в области с неподвижными границами, положение которых установлено на предыдущем шаге по времени t = t k - 1 . Из разностных аналогов уравнений (1) - (7) с помощью метода Ньютона определяется поле температуры в расчетной области и скорость движения фронта кристаллизации. Итерационная процедура метода Ньютона состоит из следующих этапов:

• 1)    По известному с предыдущего шага по времени (или с предшествующей итерации) распределению температуры на поверхности кристалла, флюса и нагревателя вычисляется эквивалентный поток излучения q eq =Rad(T ⁴ — T 4_q ) , падающий на границы д^ 2 , д^ 3 , д^ ₄ .

• 2)    Из разностных аналогов уравнений теплопроводности (1) , (2) , дополненных условиями на границах (3) – (5) ина фронте кристаллизации (6) , (7) , рассчитывается поле температуры внутри области Ω и скорость перемещения границы кристалл/расплав v g .

Затем этапы 1 и 2 повторяются. Итерации продолжаются до достижения сходимости.

Вектор скорости фронта кристаллизации v g ( t k ) , полученный на предыдущем временном шаге алгоритма, используется для определения нового положения тройной точки и формы движущихся границ. Соответствующая процедура состоит из следующих шагов:

• 1)    Вычисляется проекция v g ( t k ) := v g ( t k ) скорости фронта кристаллизации на ось Oz. Значение v g ( t k ) при r = R ( t k - 1 ) используется для определения перемещениz тройной точки в вертикальном направлении и, как следствие, подъема h ( t k ) мениска над уровнем расплава.

• 2)    По известным радиусу R ( t k - 1 ) и подъему h ( t k ) из уравнения (17) определяется контактный угол e ( t k ) . С помощью метода Эйлера из уравнения (10) , связывающего dR/dt c v g ( t k ) и tg( d ( t k ) — Q _eq ) , рассчитывается новый радиус тройной точки — R ( t k ) . Форма мениска задается приближенной формулой (18) :

r = f _men ( z,R ( t k ^( t k )) . Из равенства dZ 0 /dt = v p ( t k ) — v g ( t k ) устанавливается новое положение фронта кристаллизации Z 0 ( t k ) .

• 3)    Положение верхнего торца кристалла вычисляется из аппроксимации уравнения (12) . Форма боковой поверхности кристалла R s ( t k ) перестраивается в соответствии с аналитическим решением уравнения переноса (11) . Из закона сохранения массы (13) следует изменение высоты раслава Ah¹ ( t k ) , вызванное кристаллизацией. Положение движущихся границ корректируется: вертикальные координаты фронта кристаллизации, мениска, боковой поверхности и верхнего торца кристалла уменьшаются на величину Ah ( t k ) .

• 4.    Результаты численного моделирования

  • 4.1.    Управление изменением радиуса кристалла

Затем происходит переход на новый временной слой.

Решение модельных задач показало, что разностные аналоги законов сохранения внутренней энергии и площади ячейки выполняются в дискретной среде с высокой точностью, несмотря на существенную деформацию сетки в физической области.

Изменение объема твердой и жидкой фаз в ходе выращивания кристаллов методом Чохральского существенным образом влияет на теплоперенос в ростовой камере. Для того чтобы поддерживать рост кристалла постоянного радиуса в течение всего процесса, необходимо динамически управлять температурой нагревателя и/или скоростью вытягивания. Однако для снижения температурных напряжений, возникающих в твердой фазе, кристаллы GaAs обычно выращивают с низкой скоростью: v g < 1 см/ч. Таким образом, скорость вытягивания нельзя использовать в качестве управляющего параметра.

Изменение температуры нагревателя, в отличие от скорости вытягивания, влияет на радиус тройной точки с задержкой: соответствующим возмущениям требуется время для того, чтобы проникнуть вглубь флюса и расплава и достичь поверхности кристалла. Данное обстоятельство усложняет процесс управления и влияет на его устойчивость.

Описанная выше математическая модель может быть использована для анализа методов управления выращиванием с помощью внешнего температурного поля. Для этого систему (1) – (13) необходимо дополнить уравнением, связывающим изменение температуры нагревателя T c ( t ) в граничном условии (4) с отклонением радиуса тройной точки R от заданного значения R set :

dT c     dR

= gP It + gl(R-Rset), где gP и gI — параметры управления.

В теории управления выражение вида (19) называется пропорционально–интегральным регулятором. Его эффективность и устойчивость определяются соотношением характерных времен температуропроводности в кристалле t ^s _κ , расплаве t ^l _κ и флюсе t ^e _κ и времени t _PI , обуславливающего скорость, с которой регулятор (19) стремится изменить температуру нагревателя и обеспечить выполнение равенства R = R _set . Если t _PI <  t _K , то радиус тройной точки реагирует на изменение внешнего температурного поля с существенной задержкой, и с течением времени управление ростом кристалла может потерять устойчивость. Поэтому веса g _P и g _I в уравнении (19) необходимо выбирать таким образом, чтобы выполнялось соотношение: t PI ∼ t κ .

Для изучения влияния алгоритма управления (19) на радиус кристалла проведена серия вычислительных экспериментов, в которых использованы физические параметры кристалла, расплава, тигля и флюса, представленные в работах [5, 48, 49] . Предполагалось, что в тигель с отношением сторон H h /R c « 2 загружается 4 кг поликристаллического GaAs и 0.5 кг порошка борного ангидрида. Температура нагревателя повышается, в результате чего образуется расплав арсенида галлия, покрытый слоем флюса. В начальный момент времени затравка — кристалл радиусом 0.5R c и высотой R c / 3 , приводилась в контакт с расплавом. В качестве начального распределения температуры в расчетной области и на нагревателе использовалось решение стационарной задачи теплопроводности, в которой боковая поверхность кристалла считалась неподвижной. Характерные времена процессов в системе составляли: t _g = R c / v p « 4 • 10 4 с, t s _K = R 2 / К « 5^10 2 с, t K = R 2 / К «10 3 с. Шаг по времени равнялся т « 0.01t K .

В расчетах внутри фаз применялась сетка, равномерная в радиальном направлении (50 узлов в кристалле, 50 узлов во флюсе). Сетка в вертикальном направлении внутри расплава, кристалла и флюса сгущалась к межфазным границам (40 узлов в тигле, 100 узлов в расплаве, 100 узлов в кристалле и 30 узлов во флюсе). Для того чтобы подтвердить достоверность полученных результатов, численные эксперименты были также проведены на двух более подробных сетках: число узлов в каждом направлении увеличивалось в 2 и 4 раза соответственно. Расчеты показали, что результаты, полученные на основной и подробной сетках, отличаются менее чем на 1%.

• 4.2.    Рост кристалла при постоянной температуре нагревателя

На рисунке 4 приведены результаты моделирования режима выращивания, в котором на протяжении всего процесса температура нагревателя не изменялась, то есть gP = gI = 0 и dTc/dt = 0. Динамика движения тройной точки определяется в этом случае преимущественно переносом энергии в системе — количеством теплоты, поступающим к фронту из жидкой фазы, отводом тепла через боковую стенку кристалла, выделением энергии в ходе кристаллизации:

k ¹ (dT/dn) | z=Z 0 (t,r)- -St[v p (t) - dZ o /dt]( n • e z )= k ^s (dT/dn)| z=Z o «,г ₎₊

( а )

( в )

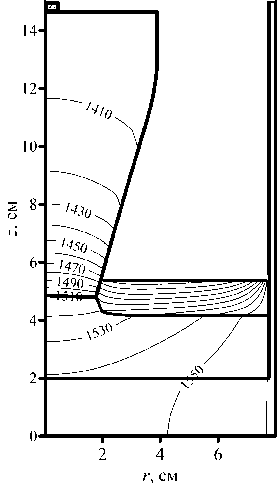
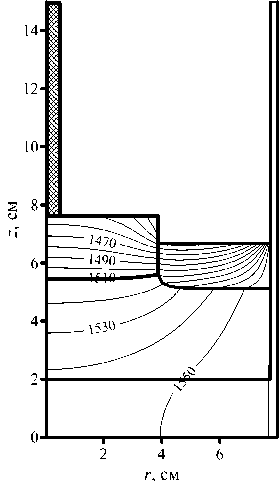
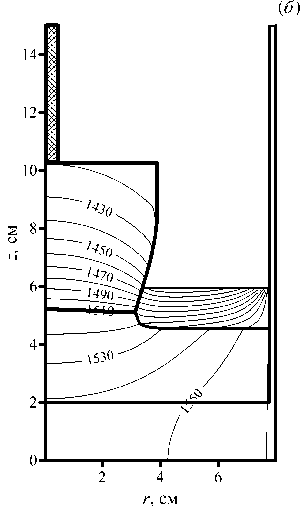
Рис. 4. Распределение размерной температуры в кристалле, расплаве, флюсе и тигле на начальной ( а ), развитой ( б ) и конечной ( в ) стадиях процесса

Результаты расчетов показывают, что увеличение площади боковой поверхности кристалла в ходе роста приводит к тому, что поток тепла через стенку и, как следствие, градиент температуры в твердой фазе в окрестности фронта кристаллизации также увеличиваются. При этом поток тепла, поступающий к фронту из жидкой фазы, на протяжении всего процесса остается практически постоянным. В этом случае, в соответствии с балансным соотношением для внутренней энергии (20) , количество кристаллизующегося материала, а значит, и радиус кристалла уменьшаются.

На развитой стадии процесса контактный угол, образующийся между расплавом и кристаллом, также почти не изменяется, и радиус кристалла уменьшается с постоянной скоростью (см. Рис. 4в ). Предложенный вычислительный алгоритм не допускает образования мениска, форма которого определяется многозначной функцией. Однако в реальном процессе контактный угол может принимать отрицательные значения, поэтому уменьшение радиуса кристалла будет происходить быстрее.

• 4.3.    Применение интегрального регулятора температуры

Для получения кристалла постоянного радиуса при его вытягивании из расплава необходимо специальным образом понижать температуру внутри ростовой камеры. При условии g _P = 0 управление (19) принимает вид:

“dtT = ^g I ^{( R —} R set ).

Такой регулятор температуры называется интегральным. Из уравнения (21) следует, что при R < R _set температура на стенке тигля автоматически понижается, а при R> R set — повышается.

Моделирование показывает, что при интегральном регулировании температуры радиус тройной точки в ходе процесса колеблется в окрестности заданного значения R = R set . Характерное поведение системы при некотором значении g I = д ^ приведено на рисунке 5, на котором видно, что частота и амплитуда колебаний радиуса с течением времени увеличиваются. Изменение температуры, происходящее на стенке тигля, проникает вглубь ростовой камеры и влияет на радиус кристалла с запаздыванием. Колебания температуры нагревателя и радиуса кристалла сдвинуты относительно друг друга по фазе (Рис. 5б ). Постепенное увеличение сдвига фаз приводит к тому, что со временем амплитуда колебаний существенно возрастает, и процесс теряет устойчивость. При увеличении веса g I наблюдается рост частоты и амплитуды колебаний радиуса кристалла.

( а )

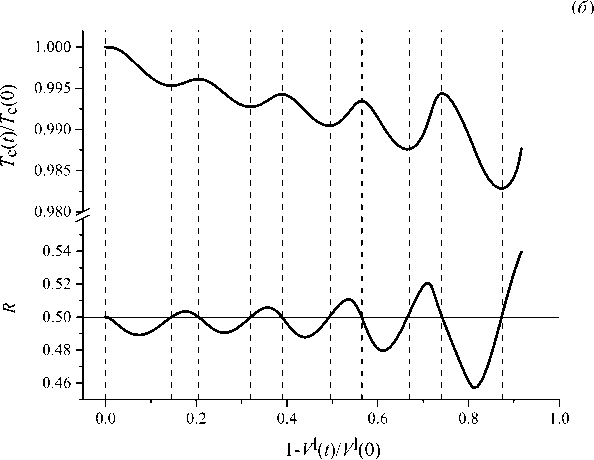
Рис. 5. Интегральное регулирование температуры, g I = g _I ^∗ : распределение размерной температуры на поздней стадии процесса кристаллизации ( а ); зависимость безразмерной температуры нагревателя T c и безразмерного радиуса тройной точки R от доли кристаллизовавшегося расплава ( б )

На рисунке 6 представлены результаты расчетов, полученные при разных g I : g^ /2 , g ^ /4 , g^ /8 . С уменьшением веса g I процесс выращивания становится более устойчивым, так как в этом случае, увеличивается характерное время t PI , изменение температуры нагревателя происходит более плавно, частота колебаний радиуса кристалла снижается. Однако на начальной стадии процесса эффективность управления падает, что приводит к росту максимального отклонения радиуса кристалла от R _set .

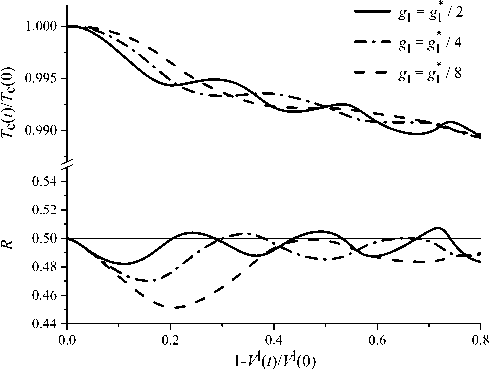
Рис. 6. Зависимость безразмерной температуры нагревателя T c и радиуса кристалла R от доли кристаллизовавшегося расплава при различных значениях веса g I

Колебания радиуса, аналогичные наблюдаемым в расчетах, описаны в классической экспериментальной работе, посвященной автоматическому управлению температурой нагревателя на основе измерений массы растущего кристалла [50] .

• 4.4.    Пропорционально–интегральное регулирование температуры

Пропорциональный член g P dR/dt в регуляторе (19) тормозит изменение температуры нагревателя в том случае, если dR/dt и ( R —R set ) имеют разный знак, что позволяет увеличить характерное время t PI без снижения эффективности управления.

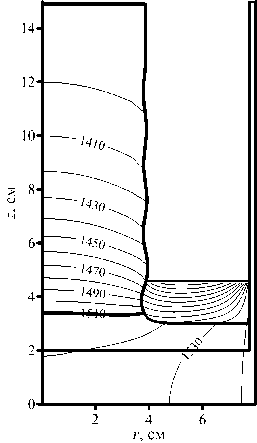
Результаты моделирования применения пропорционально–интегрального регулятора температуры представлены на рисунке 7. Вес gP = gp в уравнении (19) выбран таким, чтобы подавись колебания радиуса кристалла, возникающие при использовании чисто интегрального регулятора, то есть когда gI = д^. Рисунок 7б демонстрирует, что в ходе процесса температура нагревателя монотонно убывает, тем самым компенсируется изменение объема твердой и жидкой фаз. На развитой стадии происходит рост кристалла практически постоянного радиуса. Уменьшение веса gP приводит к тому, что, как и ранее, радиус растущего кристалла колеблется в окрестности заданного значения R = Rset (см. Рис. 8а). При этом, в отличие от расчета с интегральным регулятором температуры, частота и амплитуда колебаний с течением времени практически не изменяются.

Применение чисто пропорционального регулирования ( g I = 0 ) при умеренных значениях параметра g _P имеет следствием уменьшение радиуса кристалла (Рис. 8б ). Вместе с тем при g P >  10g p в ходе процесса радиус кристалла медленно увеличивается.

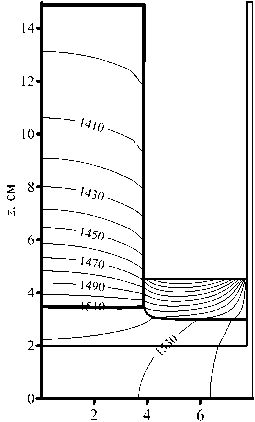
г, см

( а )

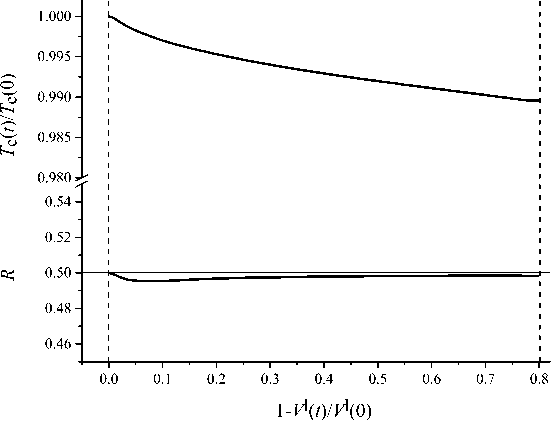
Рис. 7. Пропорционально–интегральное регулирование температуры: распределение размерной температуры в области на поздней стадии процесса кристаллизации ( а ); зависимость безразмерной температуры нагревателя T c и безразмерного радиуса тройной точки R от доли кристаллизовавшегося расплава ( б )

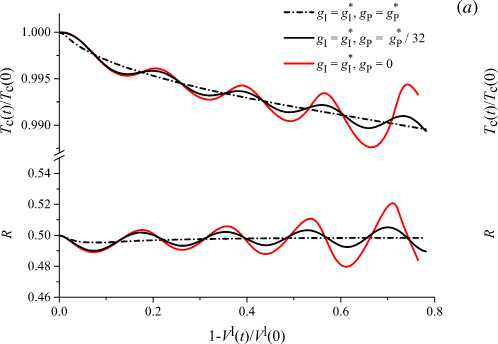
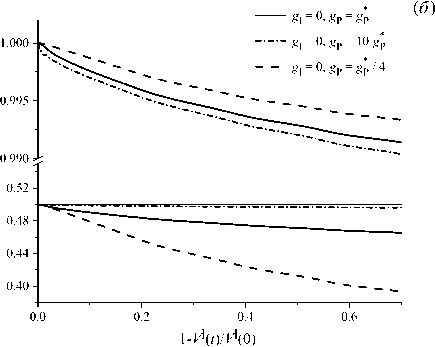
Рис. 8. Зависимость безразмерной температуры нагревателя T c и безразмерного радиуса тройной точки R от доли кристаллизовавшегося расплава при различных значениях веса g P : пропорционально–интегральный регулятор ( а ), пропорциональный регулятор ( б )

Результаты расчетов показывают, что нестационарная модель процесса (1) – (13) , дополненная уравнением (19) , может быть использована для получения приближенных зависимостей температуры нагревателя от объема расплава, обеспечивающих рост кристалла постоянного радиуса.

• 4.5.    Квазистационарная модель процесса. Сопоставление результатов расчетов

Процессы теплопереноса в рассматриваемой системе протекают существенно быстрее, чем изменяются параметры фаз (их объем, форма межфазных границ), так как имеет место условие: tg ≫ tκ. Поэтому для изучения внешнего температурного режима, обеспечивающего рост кристалла постоянного радиуса, также может применяться квазистационарная модель процесса [37, 48]. В рамках квазистационарного приближения процесс кристаллизации рассматривается как серия стационарных состояний, однозначно определяющихся внешним температурным полем, скоростью вытяжки и объемом расплава. При этом предполагается, что рост кристалла постоянного радиуса осуществляется со скоростью, равной скорости вытягивания.

Моделирование каждого из стационарных состояний осуществляется в области, изображенной на рисунке 2 при R s ( t,z) = R . В силу закона сохранения массы геометрическая конфигурация стационарных задач однозначно определяется объемом расплава V ^l . Для описания процессов теплопереноса в тигле, флюсе, расплаве и кристалле подходят уравнения (1) , (2) , записанные в стационарной форме, и граничные условия (3) – (5) . В рамках квазистационарного приближения справедливы равенство dZ 0 /dt = 0 и условие Стефана (7) , имеющее вид:

k l (dT/dn) | z=z ₀ (r) - - k s ( dT/dn )l z=Z o (r)+ = Stv g ( n^ ).

Предполагается, что скорость роста равна скорости вытягивания, то есть v _g = v p . Форма мениска определяется уравнением Юнга–Лапласа (8) с граничными условиями (9) . Условием роста кристалла постоянного радиуса является равенство контактного угла равновесному:

0 = %.

Как и ранее, при заданных радиусе кристалла R set и подъеме h тройной точки над уровнем расплава, реальный контактный угол θ может быть вычислен с помощью приближенной формулы (17) (соответствующий корень при фиксированных R , v g и T c обозначен далее как Q ( R, v g ,T _c ) ). Таким образом, условие для определения радиуса кристалла (23) записывается в виде:

6 ( R, v g ,T c )= d eq . (24)

В реальном процессе скорость роста кристалла отличается от скорости вытягивания. В работе [51] для плоского фронта кристаллизации из закона сохранения массы расплава (13) получена приближенная формула, связывающая скорости vp и vg:

^v g = ^v p

1 -

£ R ρ^l R c

- 1

Из оценки (25) следует, что для R _set = 0.5R c и 1/ p l = 1.05 реальная скорость роста превышает скорость вытягивания: v g и 1.3v _p . Поэтому, наряду с классической квазистационарной моделью, описанной выше, рассмотрена модифицированная модель, в которой скорость роста в условии Стефана (22) находится по формуле (25) .

Вычислительный алгоритм решения квазистационарной задачи подробно рассмотрен в работе [52] . Ее реализация состоит из внешнего и внутреннего итерационных процессов:

• - во внутренних итерациях при фиксированных значениях управляющих параметров ( R * ,v _g * ,T c* ) из разностных аналогов нелинейных уравнений, описывающих динамику системы, с помощью метода Ньютона определяется поле температуры в области T ( r,z ) , положение межфазных границ Z 0 ( r ) , Z 1 (r) и реальная величина контактного угла 0 ( R * , v g * ,T * ) ;

• – во внешнем цикле осуществляется поиск температуры нагревателя, обеспечивающей при фиксированных R ^∗ и v g* выполнение условия (24) . Для решения нелинейного уравнения (24) используется метод Ньютона:

°⁽R_J^v_J^Tc+hf⁽R_J^v_jTd AT = -[0(R * ,v _g * ,T c ^fe )-0 _eq ], T^¹ = Tk + AT.

Здесь k — номер итерации; 6 — шаг численного дифференцирования; значения d ( R* , v _g* ,T +5) и d ( R* ,v _g *,T ) ) определяются численно из решения соответствующих задач во внутреннем цикле итераций.

Итерационный процесс ведется до достижения сходимости. Результаты расчетов, представленные в работе [52] , показывают, что метод Ньютона сходится, как правило, за 8–10 итераций.

Для сопоставления результатов расчетов для R _set = 0.5R c в рамках нестационарного приближения ( g _P = g p , g I = g * ), с результатами вычислений по классической и модифицированной квазистационарным моделям при различных значениях V ^l во всех рассмотренных случаях использовалась одинаковая пространственная сетка. Соответствующие зависимости температуры нагревателя от объема расплава приведены на рисунке 9. Как показывают результаты расчетов, для кристаллизации 80% расплава температура нагревателя в процессе должна быть понижена на 20 К, что составляет приблизительно 1% от ее начального значения. В работе [26] рассматривался рост кристалла GaAs в близких условиях (при аналогичных геометрии тигля, массах кристалла, расплава и флюса, свойствах фаз). Падение температуры нагревателя при выращивании кристалла с R _set = 0.5R _cr также составило примерно 20 К.

Несмотря на то, что модифицированная квазистационарная модель не учитывает ряд важных особенностей технологического процесса, результаты, полученные с ее помощью, хорошо согласуются с данными нестационарного моделирования. Время счета для одного стационарного состояния даже на персональном

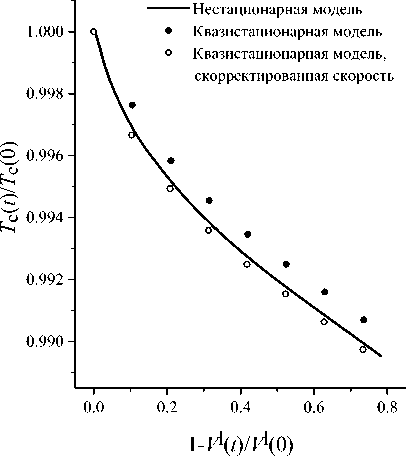
Рис. 9. Зависимости безразмерной температуры нагревателя от доли кристаллизовавшегося расплава расплава, Rset =0.5Rc компьютере составляет доли секунды. Поэтому в рамках области своего применения квазистационарная математическая модель процесса является одним из наиболее эффективных инструментов предварительного анализа технологии процесса. Более сложные и затратные с вычислительной точки зрения нестационарные модели следует применять при изучении длительных процессов, в которых форма кристалла значительно изменяется и существенную роль играет интенсивное конвективное движение в расплаве.

• 5.    Заключение

Рассмотрена нестационарная осесимметричная математическая модель процесса выращивания монокристаллов методом Чохральского, учитывающая теплоперенос в системе тигель–кристалл–расплав–флюс, образование мениска у боковой поверхности кристалла, движение фронта кристаллизации, изменение радиуса кристалла в ходе процесса. Для решения задачи с внутренними подвижными границами разработан численный алгоритм, в основе которого лежит метод выпрямления фронта и геометрически консервативная разностная схема, обеспечивающая выполнение законов сохранения массы и внутренней энергии. Предложенный подход позволяет исследовать длительные технологические режимы, в которых существенную роль играют нестационарные процессы, протекающие внутри фаз и на межфазных границах, а форма кристалла значительно изменяется по мере его роста.

В настоящей работе вычислительный алгоритм применялся для изучения методов управления радиусом кристалла с помощью внешнего температурного поля. Показано, что, если температура нагревателя на протяжении всего процесса остается неизменной, радиус кристалла с течением времени уменьшается. Использование в рамках модели интегрального регулятора температуры приводит к тому, что радиус тройной точки колеблется в окрестности заданного значения; при этом частота и амплитуда колебаний радиуса с течением времени увеличиваются. Применение пропорционально-интегрального регулятора позволяет поддерживать рост кристалла практически постоянного радиуса. В этом случае процессы переноса протекают в системе существенно быстрее, чем изменяются параметры фаз, и для описания роста кристалла можно прибегнуть к упрощенной квазистационарной постановке задачи. Вычислительные эксперименты показали, что в рассмотренном диапазоне параметров результаты, полученные в рамках квазистационарной модели, хорошо согласуются с результатами нестационарного моделирования роста кристалла постоянного радиуса. Однако детальное изучение влияния конвекции в расплаве, внешних температурных полей, скорости вытягивания и других условий выращивания на свойства полученного материала требует применения нестационарных самосогласованных моделей кристаллизации.

Автор признателен профессору О.С. Мажоровой (ИПМ им. М.В. Келдыша РАН) за обсуждение результатов и ценные замечания.