Моделирование дискретного управления противовирусным иммунным ответом в условиях неопределенности

Математические модели иммунного ответа при инфекционных заболеваниях позволяют исследовать динамику иммунной защиты организма при бактериальных и вирусных инфекциях. Данные модели, как правило, представлены нелинейными системами обыкновенных дифференциальных уравнений [1– 7], которые содержат большое количество параметров. Значения параметров моделей характеризуют биологические свойства иммунной системы и антигенов. С помощью оценки параметров, вычисленной на основе клиниколабораторных данных, можно анализировать иммунную реакцию у конкретного пациента, а также формировать наиболее подходящие схемы лечения. Решение данных задач осложняется тем, что традиционные подходы позволяют оценить параметры только к концу

заболевания, когда прогноз его течения и рекомендации по выбору лечения теряют свою актуальность. В связи с этим представляет интерес разработка методов, позволяющих строить управление в условиях неопределенности, когда значения параметров не известны, но известно, в каком диапазоне эти значения находятся, причем оценка параметров уточняется по мере накопления клиниколабораторных данных.

1. Математическая модельпротивовирусного иммунного ответа

Основной защитный механизм организма, обеспечивающий выведение антигенов, заключается в иммунной реакции, направленной только против одного, вызывающего данное заболевание, антигена. Попадая в организм, антигены начинают размножаться в клетках органа-мишени, что приводит к повреждению органа.

Иммунная реакция заключается в производстве антител, которые способны нейтрализовать антигены. Формированию антител предшествует стимуляция иммунной системы, которая состоит в образовании плазматических клеток, вырабатывающих антитела. Антигены связываются антителами, и от борьбы между ними зависит исход заболевания.

Описанная схема иммунной реакции отражена в математической модели противовирусного иммунного ответа, предложенной Г.И. Марчуком и Р.В. Петровым [3, 7]. Данная модель позволяет учитывать, как клеточный, так и гуморальный иммунный ответ. С помо-

– количество клеток-хелперов для B-клеток; B – количество B-клеток данной специфичности; P – количество плазматических клеток, синтезирующих антитела; M V – количество стимулированных макрофагов; K – концентрация донорских антител.

Функция ^ ( m ), учитывающая нарушение нормальной работы иммунной системы вследствие значительного поражения органа, имеет вид

^(m) = ‘

i, m - i

*         ,

I m - i

0 <  m <  m * , m * < m <  i.

щью модели можно строить прогнозы течения и исхода заболевания, а введение управляющих функций позволяет давать рекомендации по выбору лечения.

Одним из эффективных способов лечения инфекционных заболеваний является иммунотерапия, основанная на введении донорских антител или готовых иммуноглобулинов. Будем рассматривать модель гуморального иммунного ответа. С учетом иммунотерапии математическая модель противовирусного иммунного ответа может быть представлена в

следующем виде:

dV

-= - = a_i C V - a₃V_fF - a ₃₉ V f K - a₄V_f - ^a 5 (1 - C V - m^)V f,

-

dCV dt

= ^a 3 ₅ ^V f ⁽¹ - C V - m ) - ^a 37 C V ,

dm

— = a37cv -a38m, dt       37 V      38

dMV dt

= a V - a 7 M v ,

—T B = ^a i4A m ) ^H B ⁽ t - ^a i5 ) ^M V ⁽ t - ^a i5 ) - dt

^{- a} i6 H B M V ^{- a} i7 M V H B B + ^a i8^{(1 -} H B ),

Начальные условия характеризуют заражение здорового организма:

V_f = V °, M_r = C_v = m = K = 0,

H = B = P = F = i, B                          ,

H_B ( t ) M v ( t ) = 0, V t e [ - a ^ ,0),        (3)

M v ( t ) H_B ( t ) B ( t ) = 0, V t e [ - t,0), t = max( a ₂₆, a ₃₀).

Модель противовирусного иммунного ответа была использована для исследования динамики вирусного гепатита B.

Получен следующий набор параметров, характеризующий динамику гепатита [3]: a i = 0,1; a 2 = 10 - 4 ; a 3 = 0,1; a 4 = 10 - 4 ; a 5 = 10 - 4 ; a 6 = 0,05; a 7 = 0,02; a 8 = 10 - 4 ; a 14 = 10 - 2 ; a 15 = 1; a 16 = 10 - ³; a 17 = 10 - 4 ; a 18 = 0,05; a 25 = 0,8;

a 26 = 1; a 27 = 0,08; a 28 = 0,1; a 29 = 0,5; a 30 = 1; a 31 = 0,16; a 32 = 0,17; a 33 = 0,2; a 34 = 0,17; a 35 = 0,4; a 36 = 0,002; a 37 = 0,005; a 38 = 0,12; a 39 = 0,1; a 40 = 0,2; a 41 = 0,17.

dB

— = ^a ₂ 5 ^( m ) M v ⁽ t ^{- a} ₂ 6 ) H B ⁽ t ^{- a} 26 ) ^{B (} t ^{- a} 26 ) dt

-

- a^M VH B + a9 о (i - B), 2/ V B         28'- dP a29 ^(m)Mv (t  a30)HB (t  a30)B(t  a30) + dt

^{+ a} 3i ^{(i -} P ),

— = a₃₂P - a₃₃FV_f - a^F ,

dK

— = u

dt

^{- a} 40 KV f

- a _4i K .

Фазовыми переменными модели являются: V f – концентрация свободного вируса; F – концентрация антител к вирусным антигенам; C V – доля зараженных клеток органа-мишени; m – доля пораженных клеток органа-мишени; H B

2. Алгоритм управленияв условиях неопределенности

Будем считать, что клиниколабораторные данные можно получить в определенные моменты времени, которые соответствуют узлам сетки

П = {t : t = i A t , i = i N , A t = T / N }.   (4)

Таким образом, входная информация имеет дискретный характер.

Управляющая функция u = u ( t ), характеризующая скорость введения донорских антител, выбирается из множества

U =

'u ( t ). u ( t ) = u i ₄5( t - t i J, ^ _Ul_ ! е [0, b ], i = V N

где параметр b >  0 учитывает физиологически допустимые дозы применения лекарственных препаратов, 8 - дельта-функция.

Для построения управляющей функции в условиях неопределенности использовался алгоритм, предложенный в работе [8].

Методика построения программы лечения заключается в следующем. Для параметров модели выбирается диапазон допустимых значений:

a i е [ a - , a* ], i = 1, L ,                ⁽⁶⁾

где L - количество параметров.

На множестве допустимых значений параметров случайным образом задается K наборов параметров:

a ⁽ k ) е0 , к = 1, K ,               (7)

где

0 =

а: aj = ai + jhi, j = 0, Mi, +     — h = ai - ai , i = 1,L iM

При t е П определяются допустимые наборы параметров, которые удовлетворяют критерию

|V_f ( t, a^{( k} ) ) - V-(t i ) < 8 1 ,

,            _____ _____ (9)

|m(t,, a(k)) - m '"(t,)| < s2, i = 0, N, к = 1,K, где VЭксп'(t.), mэксп' (t) - полученные на основе анализов клинико-лабораторные данные;

£j, j = 1,2 - величина допустимого отклонения расчетных значений соответствующих фазовых переменных от клиниколабораторных показателей; K - количество наборов параметров в момент времени ti;

a = ( a , a ₂,..., a_L ) .

Таким образом, после определения значений фазовых переменных модели в момент времени t = t_i необходимо получить K, решений задачи (1)-(3) на отрезке [0, t_i ] , i = 0, …, N , а также определить допустимые наборы значений параметров.

Предварительная оценка параметров определяется при t = ti по формуле aj1

J i

Za к=1

J i

, j = 1, L , i = 0, N ,

где J - количество допустимых наборов параметров в момент t_i ; J < K , i = 0, ..., N ; K = J j , i = 1, ., N ; K _o = K , где K - первоначальное количество наборов параметров; J = K - H , i = 0, ., N , где H - количество неприемлемых наборов в точке t .

Для формирования управляющей функции применялся алгоритм, предложенный в работе [9]. Идея алгоритма заключается в том, что динамику антигенов необходимо вывести на желаемое состояние, которому соответствует некоторое решение математической модели противовирусного иммунного ответа. Это решение названо опорным. Значения концентрации антигенов, полученные из опорного решения, заданы на сетке (4):

V f ( t i ), i = 1, N .                 (11)

С использованием предварительной оценки параметров (10) вычисляются прогнозируемые значения фазовых переменных на следующий момент времени. Если прогнозируемый уровень концентрации антигенов не совпадает с опорным значением, то в качестве управления U i подбирается такая величина, которая обеспечивает перевод фазовой траектории антигенов в желаемую точку. Итоговая оценка параметров находится по формуле (10) при i = N .

3. Результаты вычислительных экспериментов

Рассмотрим построение программы лечения при острой форме заболевания. В этом случае опорное решение можно определить исходя из минимизации функционала энергетической цены иммунного ответа [9]:

T

E = a 29 1 ^M V ⁽ t ^- a 26 ) ^H B ⁽ t ^- a 26 ) ^{B (} t ^- a 26 ) ^ min •    (12)

На рис. 1 изображена зависимость энергетической цены иммунного ответа от коэффициента стимуляции иммунной системы при нулевом значении параметра запаздывания.

Опорное решение будем определять при a 29 = 3,5 и a 26 = 0.

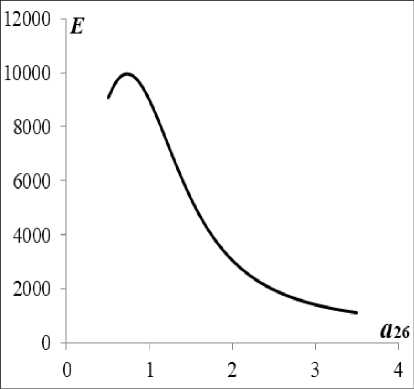
Рис. 1. Энергетическая цена иммунного ответа

Для построения управляющей функции в условиях неопределенности будем использовать имитацию клинико-лабораторных показателей. Экспериментальные значение в критерии (9) зададим из решения модели при известных значениях параметров. Далее, считая значения параметров неизвестными, будем строить управление и одновременно уточнять значения параметров.

На рис. 2 сплошными линиями показано изменение концентрации донорских антител. Величины скачка функции определяют объем вводимых в соответствующий момент времени донорских антител. Также на рисунке представлена динамика антигенов при естественном течении заболевания (штриховая кривая) и в случае рассмотренной программы лечения (штрих-пунктир). В формуле (2) принято m * = 0,1. Считалось, что в момент инфицирования V 0 = 10 ^{- 6} . В выражении (5) в качестве ограничения на скорость введения препаратов взято значение b = 50. В условии (7) принято ^ = 10 4 , а в критерии (9) взяты следующие значения: e i = 0,01; 6 2 = 0,25.

Программа лечения заключается в постепенном увеличении объема вводимых донорских антител. Максимальная концентрация антигенов снижается в два раза.

Полученные результаты хорошо согласуются с вариантом непрерывного введения донорских антител, поученным в работе [10].

В ходе построения управления в условиях неопределенности неизвестными считались десять параметров, которые оказывают наиболее существенное влияние на изменение решения. Значения остальных параметров были заданы.

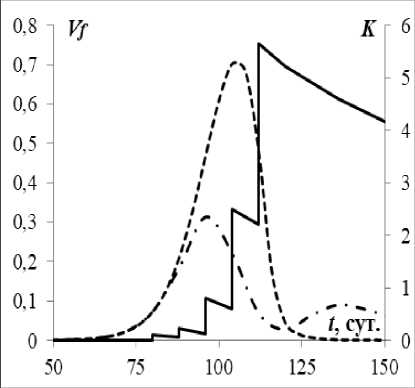
Рис. 2. Дискретное управление иммунным ответом

В таблице представлены результаты оценки параметров. Для каждого параметра определены границы диапазона допустимых значений, а также шаг сетки. Максимальная погрешность оценки параметров составляет 10,0 %, а средняя – 6,4 %.

Результаты идентификации параметров

a i	a i	a	h i	Оценка параметров
a 1	0,085	1,115	0,006	0,109
a 2	0,085	1,115	0,006	0,103
a 5	0,045	0,055	0,002	0,055
a 7	0,0095	0,0105	0,0002	0,0097
a 12	0,75	0,85	0,02	0,750
a 16	0,45	0,55	0,02	0,550
a 19	0,165	0,175	0,002	0,171
a 20	0,15	0,25	0,02	0,190
a 22	0,35	0,45	0,02	0,370
a 23	0,0045	0,0055	0,0002	0,0049

Таким образом, рассмотренный алгоритм позволяет строить программы лечения и получать приемлемую оценку параметров.

Заключение

Результаты вычислительных экспериментов с моделью противовирусного иммунного ответа показывают, что иммунотерапия позволяет проводить эффективное лечение при острой форме заболевания.

С помощью рассмотренного алгоритма можно строить управление иммунным ответом в условиях неопределенности, уточняя оценку параметров по мере поступления новых клинико-лабораторных данных.