Моделирование дисперсионного анализа в электронных таблицах и оценка мощности критерия при разложении ошибок на составляющие

Сравнительно недавно опубликован национальный стандарт Российской Федерации [1], в котором впервые вводится понятие и способы применения мощности критерия (теста) при проверке статистических гипотез о средних и дисперсиях. Эти методики предназначены, в первую очередь, для статистической оценки качества. Показатели качества ряда продуктов во многом определяются показателями качества химического анализа [2, c. 107]. Однако в учебной и методической литературе по химической метрологии [2–4] раскрытию понятия и количественной оценке мощности критерия уделяется, с нашей точки зрения, недостаточно внимания. Так в [4, гл. 12.1.2] при раскрытии темы по статистическим тестам в качестве основных этапов теста называют: 1) выбор подходящего критерия, 2) выбор уровня значимости, 3) формулирование нуль-гипотезы (Н 0 ) и альтернативной гипотезы (Н а ), 4) вычисление тестовой статистики и ее сравнение с критическим значением. В этой последовательности не хватает заключительного этапа – не хватает оценки мощности теста, характеризующего надежность статистического вывода вероятностью непринятия Н₀, когда верна Н_а. Как считают авторы [5]: «Мощность критерия позволяет углубить выводы, полученные при испытании гипотез». Применительно к алгоритмам дисперсионного анализа, которые описаны в [6], аналогичные рекомендации высказывают авторы работ [7]. Критикуя ГОСТ Р ИСО 5725-2–2002, авторы [7] приходят в выводу: «Поэтому чтобы стандарты и информационные технологии «заработали» корректно, необходимо, прежде всего, преодолеть статистическую безграмотность специалистов, практиков».

Компьютерные технологии обучения при их реализации в электронных таблицах, содержащих богатый набор средств тестовой статистики и стохастического моделирования, должны эффективно использоваться при преподавании вузовских курсов химической метрологии (и не только…). Это, в свою очередь, ставит задачи по разработке нового инструментария для моделирования различных ситуаций (сценариев) при химическом анализе и обработке его результатов. Данная работа является продолжением серии публикаций [8, 9] по этой тематике.

Принципы и технологию построения стохастических моделей рассмотрим на примере построения матрицы плана однофакторного дисперсионного анализа. План включает измерения результирующего признака X j (концентрации) в аналитических сериях j = 1, n , в каждой из которых выполняют i = 1, m параллельных измерений. Модель строим исходя из основных предположений дисперсионного анализа: выборки получены из нормальных совокупностей с математическими ожиданиями М ( Х 1 )^ М ( Х_п ) и одинаковой дисперсией о ². Эти положения записывают уравнением:

X j = M ( X ) + e j + e j . (1)

Случайную величину e j называют факторным эффектом, e ij – остаточным эффектом. С учетом принципа, который называют методом обратных функций Монте-Карло [10, с. 321] уравнение (1)

перепишем в виде:

X_ij = M ( X ) + N ^{- 1}( r ) ⋅σ ^* + N ^{- 1}( r ) ⋅σ ₁ или

Xij =N-1(r,0,σ*)+N-1(r,M(X),σ1), где r – равномерно распределенные на интервале (0, 1) случайные числа. Уравнения (2) являются основой для генерирования выборочных матриц плана однофакторного дисперсионного анализа. Заметим, что метод обратной функции является универсальным методом генерации псевдослучайных чисел по любому закону распределения.

Для наглядности изложения нашего метода возьмем в качестве примера результаты, полученные в [2, c. 140]. Решается задача о вкладе погрешности пробоотбора антифрикционного сплава в общую погрешность определения массово й концентрации сурьмы. Для шести кернов сплава выполняют определение сурьмы (% Sb) в двойной повторности для к аждого керна:

14,72            15,51

15,05            15,23

14,60            15,10            14,70            14,74

14,35            15,23            14,95            14,50

В результате дисперсионного анализа найдены характеристики разб р оса межд у сериями, внутри серий и дисперсию пробоотбора: s 21 = s 22 + ns 2* = 0,2219; s 22 = 0,0326; s 2* = ( s 21 – s 22 )/ n = = 0,0942 соответственно.

Воспользуемся результатом [2] для оценки параметров уравнений (2). Среднее значение результата анализа примем в качестве оценки M ( X ) = 14,89. В качестве оценок σ 1 и σ * примем s 1 и s * . При вычислениях мощности критерия будем использовать параметр λ 2 = σ 21 / σ 22 = 6,81.

На рис. 1 показана форма листа электронной таблицы, которая содер ж ит массив ячеек, связанных формулами. Расчетные формулы в нотация х MS Excel приведены в табл. 1. О собенностью вычислений является то, что, во-первых, факторные эффекты генерируют независимые датчики вида НОРМОБР(СЛЧИС();0;$C$5^0.5), число к оторых равно числу уровней фактора, а остаточные эффекты генерируют датчики вида НОРМОБР(СЛЧИС();$C$3; $ C$4^0.5)+ B $8, число которых равно размерности матрицы плана. Во-вторых, факторные эффекты передаются по ссылке из массива погрешностей B8:G8 в ячейки ма т рицы плана B10:G11. В данном примере гипотеза об однородности дисперсий не проверяется, поскольку ее справедливость изначально заложена в модели. Правильность результатов дисперсионного анализа с использованием формы на рис. 1 проверяли расчетами с использованием утилиты Excel «Однофакторный дисперсионный анализ» из надстройки «Анализ данных». Результаты совершенно идентичны.

A

J____В

С , D | Е | F | G , К

Стохастическая модель дисперсионного анализа

Параметры модели

x(Sb), масс % сг (анализа)=

14.89

0 0326

□ 0942

Генерирование матрицы плана однофакторного дисперсионного анализа 1) погрешностей пробоотбора шести кернов баббита

0.5947 -0.2541 -0.2923

0.0963

-0.1378

0.1827

14.83

14.87

15.07   14.82   15.39   14.62   14.13

14.70   15.02   15.40   14.56   14.59

2) погрешностей анализа и их смешивания с погрешностями пробоотбора

Разложение ошибок (дисл анализ)

СрЗнач         14.85     14.89   14.92   15.40   14.59   14.36

Дисперсия    0.0006    0.0699  0.0204  0.0001  0.0019  0.1081

s2,= 0.2434 F= 7.27

Мощность критерия ЧиспИсп= 498

ЧислУдач= 160

s²₂= 0.0335               s²’= 0.1049

>больше> 4.39 = F(a.,f1,f2)

68%

Рис. 1. Форма листа Excel для моделирования мощности критерия

Моделирование дисперсионного анализа в электронных таблицах и оценка мощности критерия при разложении ошибок на составляющие

Таблица 1

Формулы в ячейках на рис. 1

Ячейки	Функции
B8:G8	НОРМОБР(СЛЧИС();0;$C$5^0.5)
B10:G10	НОРМОБР(СЛЧИС();$C$3;$C$4^0.5)+B$8
B11:G11	НОРМОБР(СЛЧИС();$C$3;$C$4^0.5)+B$8
B13:G13	СРЗНАЧ(B10:B11)
B14:G14	ДИСП(B10:B11)
B15	СЧЁТ(B10:B11)*ДИСП(B13:G13)
D15	СРЗНАЧ(B14:G14)
G15	ЕСЛИ(B16>D16;(B15-D15)/СЧЁТ(B13:B14);0)
B16	B15/D15
C16	ЕСЛИ(B16больше>")
D16	FРАСПОБР(0.05;СЧЁТ(B10:G10)-1;СЧЁТ(B10:G10)*(СЧЁТ(B10:B11)-1))
B18	(B18+1)
B19	ЕСЛИ(B16>D16;B19;B19+1)
E19	1-B19/(B18-1)

Удобство использования нашего алгоритма состоит, во-первых, в возможности многократного прогона процедур анализа и, во-вторых, в автоматизации стадии статистического вывода. (Обратим внимание на блок ячеек A16:G16.) Предложенный нами алгоритм обладает достаточной гибкостью для того, чтобы перестраивать форму под задачи с матрицами плана большего или меньшего размера. В учебных целях можно легко изменять сценарий. Например, факторными эффектами могут быть погрешности при анализе в условиях внутрилабораторной прецизионности или межлабораторная ошибка.

Многие особенности дисперсионного анализа можно исследовать, не прибегая к эксперименту, например, исследовать его основные предположения. Апостериорное использование рассмотренного подхода может способствовать углублению обоснованности статистических выводов из лабораторных экспериментов.

Дополнительно к традиционному представлению результатов дисперсионного анализа разработанная нами вычислительная форма позволяет исследовать, с использованием техники Монте-Карло, эффективность разложения погрешностей. При многократных прогонах программы и подсчете процента случаев успешной дискриминации ошибки пробоотбора получаем оценку мощности (эффективности) теста Фишера. Мощность принято обозначать как дополнение к ошибке второго рода: 1 – β .

Подсчет числа случаев, когда принимается альтернатива Н а : σ 21 ≥ σ 22 против Н 0 : σ 21 = σ 22 , осуществляется с помощью сконструированного нами счетчика, который работает в итерационном режиме и изменяет показания при пересчете листа. Причем встроенный в Excel датчик случайных чисел R ( r |0,1) также обновляет значения при пересчете листа. Для того чтобы создать счетчик, пользователю следует установить на вкладке «Вычисления» переключатель «вручную», активировать флаг «итерации» и назначить предельное число итераций равное 1. Итерационный процесс осуществляется с использованием формул, записанных в ячейках В18; В19; Е19 (см. табл. 1). Для запуска счетчика следует нажимать/удерживать клавишу F9. Чтобы после завершения серии испытаний привести счетчик к исходному состоянию, следует установить фокус на ячейке В18 и двойным щелчком войти в формулу. Последующий ввод формулы клавишей «Enter» приведет к отображению числа 1. Аналогичная процедура установит в ячейке В19 число 0/1, в зависимости от сообщения «больше/меньше» в ячейке С16.

Вероятность отвергнуть Н 0 , когда верна альтернативная гипотеза Н а , вычисляется как относительная частота события «ЧислУдач» по формуле, записанной в ячейке Е19. На рис. 1 видим, что потребовалось около 500 испытаний модели, при которых показатель мощности в ячейке Е19 перестает изменяться. Для получения такого результата требуется не более 30 секунд.

Результаты испытания эффективности F-теста с данными [2] приведены на рис. 1 в ячейке Е19. Заметим, что специалисты фирмы StatSoft [11] считают приемлемой мощность теста не меньшую чем 80 %. Мощность теста следует усилить. Есть четыре основные стратегии повыше- ния мощности: выбор более высокого уровня ошибки первого рода а, формулирование направленных гипотез, увеличение объема выборки и усиление эффекта. Для нашего случая наиболее важным представляется увеличение размерности матрицы плана, а также осуществление мероприятий по усилению изучаемого эффекта. Очевидно, что эффект будет усилен при повышении точности измерения результирующего признака, т. е. при уменьшении величины 02. В вычислительной среде нашего алгоритма доступным остается только увеличение размерности матрицы плана. Априори не ясно следует ли увеличить число параллельных опытов m или более эффективным будет увеличение числа проб n? (Хороший вопрос для проблемного обучения.) Однако имеется иной способ решения задачи, который следует из теории статистических тестов. Мощность критерия можно вычислить [1, 5], не используя технику Монте-Карло.

Исходя из принципов, которые обосновываются в руководствах по м атематической статистике, для нашей задачи запишем:

F 1 -P ( К,f = ) = F a ^ ff . (3) Л

То есть квантиль распределения Фишера - Снедекора для вероятности 1 - в можно вычислить с использованием таблиц F-распределения. Поскольку уровень значимости в задачах химического анализа обычно принимают равным 5 %, то соответствующая ему квантиль известна. Известен также параметр Л2 = о21/о22.Тогда искомое значение мощности можно найти по тем же таблицам, исходя из выражения:

1 -в = P ( F ( f , f 2) > F ^{a ( f} 2 , f ² ) k              ^Л

Встроенные в электронные таблицы библиотеки статистических функций, существенно облегчают задачу обращения к статистическим функциям. Поэтому уравнения (3) и (4) д ля работы в среде Excel можно записать одной формулой:

=FРАСП(FРАСПОБР( a f;f)) Л ²; f;f . ), (5) которая сразу возвращает значение мощности крите р ия. В этой формуле в отличие о т предыдущих вместо адресов ячеек целесообразнее использовать их имена.

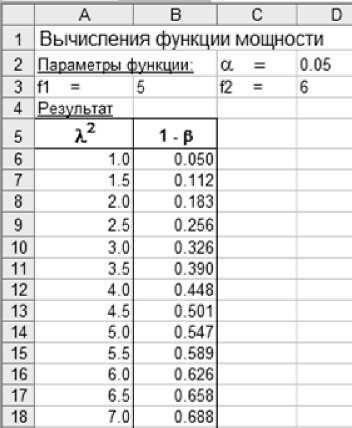
Рис. 2. Фрагмент формы для вычислений функции мощности

С использованием нашей функции (5) весьма просто вычислить так называемые функции мощности, которые в виде графиков проводят в [1]. Приме р организа ц ии вычислений таких функций показан на рис. 2.

При создании этой формы в В6 записывают формулу FРАСП(FРАСПОБР($D$2;$B$3;$D$3)/A6;$B$3;$D$3), которую затем копируют ниже по столбцу с помо щ ью функции автозаполнения. Посредством формы на рис. 2 можно генерировать в с евозможные графики для испытаний Фишера и не только при равенстве f 1 = f 2 , как это делается в [1]. Более того, для отыскания параметров функции мощности практически отпадает необходимость в утомительной процедуре графич е ской интерполяции.

Подставляя в ячейки на рис. 2 значения параметров для задачи с кернами, получаем 1 —в = 68 %, что не отличается от результата метода Монте-Карло на рис. 1. Согласие в результатах, с одной стороны, указывает на справедливость формулы (5), и, с другой стороны, говорит о надежности нашего алгоритма статистических испытаний. Этот результат также косвенно указывает на качество ис- пользованного нами генератора случайных величин. Мы использовали самый простой генератор

нормально распределенных величин без цифровой фильтрации «промахов» по правилу 3о, и ок- ругления данных для учета дискретности измерительных шкал.

Теперь решим задачу по оптимизации матриц ы плана дисперсионно г о анализа в задаче с кернами. Для этого используем технику сценариев «Что если?» и вычисления по уравнению (5). Испытанные нами сценарии приведены в табл. 2. Видим, что увеличение числа проб по Сцена-

Моделирование дисперсионного анализа в электронных таблицах и оценка мощности критерия при разложении ошибок на составляющие рию 2 на две единицы, против базового Сценария 1, позволяет удовлетворить требованиям эффективности теста: 1 – β ≥ 80 %. Такого же результата достигаем в Сценарии 3. Здесь число проб меньше чем в Сценарии 2, но число опытов больше из-за увеличения числа параллелей до 3. Пожалуй, наиболее оптимален Сценарий 4, при котором число измерений не многим больше числа измерений по Сценарию 2, но трудозатраты на пробоотбор и пробоподготовку меньше (при очевидном выигрыше в надежности статистического вывода).

Таблица 2

Результаты испытаний «Что если?» ( λ² = 6,81, α = 0,05)

Сценарий	m	n	m × n	f 1	f 2	1 – β
1	2	6	12	5	6	0,68
2	2	8	16	7	8	0,80
3	3	6	18	5	12	0,80
4	3	7	21	6	14	0,85
5	3	8	24	7	16	0,89

Рис. 3 иллюстрирует возможности алгоритма генератора «Вычисления функции мощности» для визуализации результатов его работы. На рис. 3 показаны функции мощности для сценариев в табл. 2. Пунктирная линия соответствует λ ² = 6,81.

Очевидно, что исследования мощности критерия методом Монте-Карло и методами тестовой статистики взаимно дополняют друг друга. Чем больше методов для решения одной и той аналитической задачи, тем надежнее не только обработка результатов, но и выводы из результатов химического анализа. Сочетание названных методов особенно полезно при преподавании химической метрологии и хемометрики, поскольку это отвечает требованиям современной дидактики, приоритетами которой являются компьютерные технологии, активные формы обучения, проблемное обучение, наглядные методы и повышение уровня мотивации к обучению.

Результаты работы могут быть востребованы при реализации концепции открытого образования и научных вычислительных веб-сервисов.

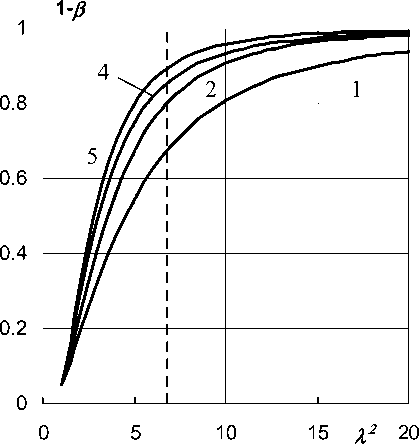
Рис. 3. Функции мощности для сценариев (номера на рисунке соответствуют номеру сценария в табл. 2)