Моделирование доходности акций компаний различной страновой и отраслевой принадлежности

Особенностью современного этапа развития как национальной, так и глобальной экономики является ее функционирование в условиях нестабильности, неопределенности, сложности и неоднозначности.

Динамично развивающаяся в условиях неопределенности и повышенной волатильности рыночная среда ставит перед субъектами, принимающими решения, нестандартные задачи, которые либо с трудом решаются традиционными методами, либо полученные решения не дают желаемого эффекта. Сложность таких задач заставляет искать новые подходы к использованию различных аналитических приемов и методов, обосновывающих принятие конкретного управленческого решения. Особенно это заметно при выборе метода формирования инвестиционного портфеля. Портфельная теория основана на статистическом анализе, целью которого является выбор оптимального соотношения между доходностью и риском инвестиций. Применение современных статистических методов, позволяющих получать робастные оценки доходности и риска ценных бумаг, позволяет принимать более взвешенные инвестиционные решения.

Наиболее распространенным подходом к оценке уровня премий за акционерный риск, используемым на практике основными инвестбанками и аудиторами, а также широко описанным в научной литературе, является модель САРМ (Capital Asset Pricing Model) предложенная Уильямом Шарпом и Джоном Линтнером [11, 8]. Одной из причин популярности этой модели во второй по- ловине XX века является простота расчета ожидаемой доходности долгосрочного актива. Такая оценка осуществляется относительно всего рыночного портфеля. Однако крупным недостатком CAPM является предположение о нормальности распределения доходностей активов, что противоречит эмпирическим наблюдениям. Современный уровень развития компьютерной техники позволяет повысить точность моделирования доходности в ущерб вычислительной простоте. Важной характеристикой совместного распределения доходностей финансовых активов является асимметрия в их взаимосвязи [1, 5, 10]. Эта асимметрия заключается в том, что цены акций сильнее склонны к совместному снижению, чем к совместному росту, более того, степень асимметрии может варьироваться для различных пар финансовых активов. В настоящей статье предлагается метод, позволяющий повысить эффективность деятельности инвестиционных и паевых фондов, путем увеличения точности прогнозирования доходности активов.

Теория

Гибким способом учета асимметрии совместного распределения доходностей является использование конструкций из парных копул (далее – КПК).

Использование условных парных копул при моделировании многомерных распределений было впервые рассмотрено в работе Гарри Джо [7]. В трудах Бедфорда и Кука [2, 3] была предложена графическая модель «правильных ветвлений», которая является удобным способом наглядного представления (в виде многоуровнего графа) разложения функции плотности распределения на произведения плотностей парных копул и плотностей частных распределений. В работе Дж. Дисс-мана и др. [6] предложен способ выбора оптимальной структуры, основанный на максимизации суммарного коэффициента корреляции Кендалла на каждом уровне графа (метод максимального остовного дерева). Этот метод структурирования КПК чаще других используется в научной литературе, тем не менее, у него есть существенный недостаток – в случае появления сильной ложной корреляции между доходностями активов, формируется структура КПК, обладающая плохой прогностической силой. Способ решения этой проблемы был предложен в работе Айка Кристиана Брехмана и Клаудии Кзадо [4]. Авторы предложили ввести в КПК на правильных ветвлениях страновые и отраслевые фондовые индексы для выделения системной компоненты риска. Тем не менее, они существенно ограничили структуру КПК, используя независимую условную копулу для моделирования совместного распределения доходностей пар национальных фондовых рынков, а также используя Гауссову копулу для моделирования условных совместных распределений доходностей активов на «старших» уровнях ветвления. Эти ограничения были установлены для того, чтобы максимально приблизить КПК к CAPM, кроме того, они позволили сократить время оценки параметров модели. В приложении к моделированию на финансовых рынках, КПК представляют собой способ задания совместного распределения доходностей активов в виде комбинации парных1 копу-ла-функций условных и безусловных частных распределений доходностей каждого из них. Парной копулой называется совместная функция распределения двух случайных величин, в которой в качестве аргументов рассматриваются две функции частных распределений (условных или безусловных). Плотностью парной копулы называется ее производная по двум аргументам.

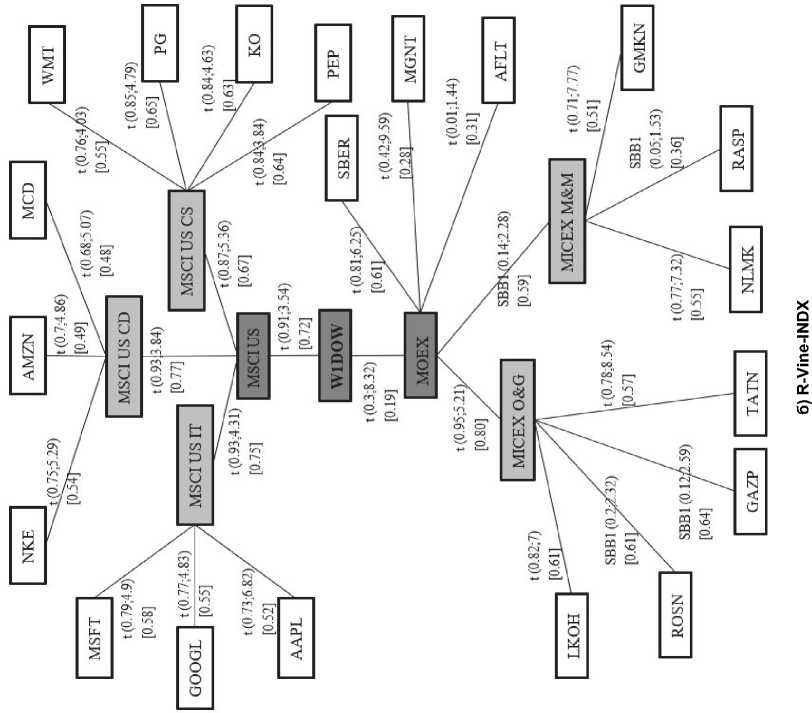
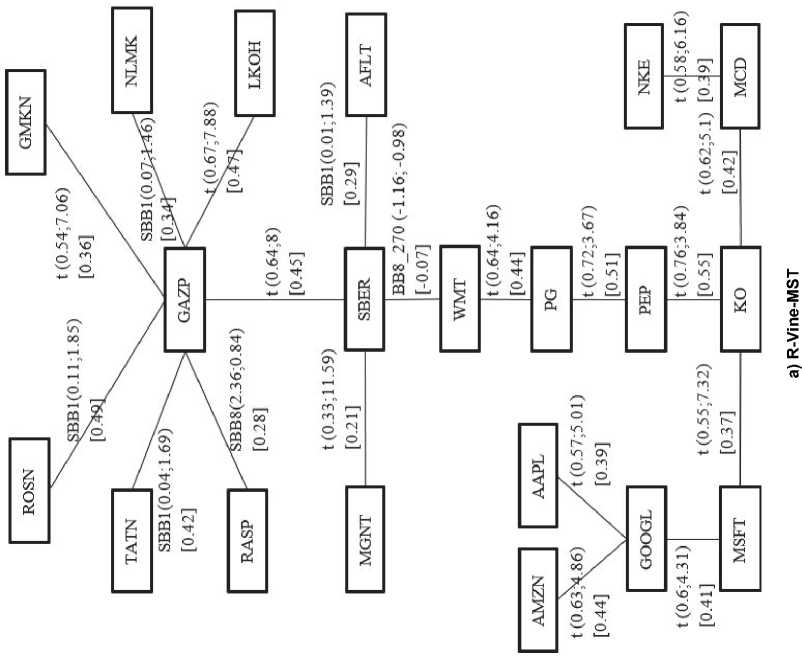
Наиболее распространенным в научной литературе способом выбора структуры КПК является метод максимального остовного дерева (R-Vine-MST), заключающийся в выборе структуры каждого уровня модели таким образом, чтобы максимизировать сумму коэффициентов корреляции Кендалла для всех парных копул представляемых ребрами этого графа. Тем не менее, корреляция не всегда говорит о реальной взаимосвязи между случайными величинами. Существует эффект ложной корреляции, который, при использовании метода максимального остовного дерева, может привести к выбору структуры, не отражающей реальной взаимосвязи между доходностями акций. Для того, чтобы ограничить влияние ложной корреляции на качество модели распределения доход- ностей, рассмотрим в качестве альтернативного метод (R-Vine-INDX), при котором первое дерево ветвления структурировано жестко по отраслевому и страновому принципу с помощью фондовых индексов, а остальные уровни ветвления формируются по принципу максимизации суммы коэффициентов корреляции Кендалла.

Результат

Для того, чтобы оценить эффективность предлагаемого метода структурирования КПК, было проведено его сравнение с обыкновенным методом максимального остовного дерева в рамках решения задачи формирования оптимального инвестиционного портфеля из акций российских и американских компаний. В качестве критериев оптимальности были приняты два показателя: минимум ожидаемых потерь (CVaR, 95%), характеризующий ожидаемую абсолютную доходность портфеля в пяти процентах наихудших случаев и максимум коэффициента Шарпа ² .

В табл. 1 приведен перечень ценных бумаг и индексов, дневные доходности которых использовались при сравнении эффективности использования различных методов структурирования первого дерева КПК. Для проведения исследования отбирались ликвидные акции, принадлежащие компаниям из различных секторов экономики каждой из стран.

На рис. 1 представлены первые два дерева КПК, полученные с использованием различных методов задания структуры (R-Vine-MST и R-Vine-INDX) для дневных доходностей акций российских и американских компаний за период с 01.01.2007 г. по 23.12.2016 г. Рядом с каждым ребром дерева указан вид парной копулы, ее параметры в круглых скобках и значение коэффициента ранговой корреляции Кендалла, в квадратных скобках. При построении КПК, первые деревья которых представлены на рис. 1, рассматривались все парные копулы (t, Гаусса, Клейтона, Гумбеля, Франка, Тауна, Джо, BB1, BB6, BB7, BB8 и их вращения), доступные в библиотеке «VineCopula» [12] среды программирования R. Из рисунков видно, что в структуре преобладают парные копулы Стьюдента, что связано с достаточно длительным (10 лет) периодом оценки параметров, в то время как асимметрия во взаимосвязи между доходностями акций проявляет себя на более коротких интервалах (до трех лет). Из рис. 1 а также видно, что ценные бумаги склонны к объединению в кластеры по отраслевому и страновому принципу при использовании метода максимального остовного дерева.

Таблица 1

Перечень акций и фондовых индексов

Тикер (обозначение)	Наименование акционерного общества/индекса
Акции российских компаний
AFLT	ПАО «Аэрофлот – российские авиалинии»
GAZP	ПАО «Газпром»
GMKN	ПАО «ГМК «Норильский никель»
LKOH	ПАО «Лукойл»
MGNT	ПАО «Магнит»
NLMK	ПАО «Новолипецкий металлургический комбинат»
RASP	ПАО «Распадская»
ROSN	ПАО «НК «Роснефть»
SBER	ПАО Сбербанк
TATN	ПАО «Татнефть»
Акции американских компаний
AAPL	Apple Inc.
AMZN	Amazon.com, Inc.
GOOGL	Alphabet Inc.
KO	The Coca-Cola Company
MCD	McDonald's Corporation
MSFT	Microsoft Corporation
NKE	NIKE Inc.
PEP	PepsiCo, Inc.
PG	The Procter & Gamble Company
WMT	Walmart Inc.
Отраслевые и страновые фондовые индексы
W1DOW	Dow Jones Global Index
MOEX	Индекс МосБиржи
MICEX O&G	Индекс ММВБ Компаний нефтегазового сектора
MICEX M&M	Индекс ММВБ Горно-металлургического сектора
MSCI US	MSCI USA Index
MSCI US CS	MSCI USA Consumer Staples Index (индекс акций компаний – производителей товаров массового потребления и ретейлеров)
MSCI US CD	MSCI USA Consumer Discretionary Index (индекс акций компаний – производителей второстепенных товаров)
MSCI US IT	MSCI USA Information Technology Index

Для тестирования моделей оптимизации портфеля был использован метод скользящего окна, характеризующийся следующими условиями:

• •    в качестве горизонта тестирования моделей оптимизации выбран период с 01.01.2009 г. по 23.12.2016 г.;

• •    портфель пересматривался в начале каждого квартала;

• •    оценка параметров КПК осуществлялась на данных о дневных, простых доходностях акций и фондовых индексов за два года, предшествующих моменту оптимизации портфеля;

• •    в качестве безрисковой доходности для расчета коэффициента Шарпа использовалась ставка MIBOR со сроком от 31 до 90 дней;

• •    в качестве частных распределений доходностей рассматривались эмпирические функции (использовались рублевые доходности).

Были установлены дополнительные ограничения на структуру активов в портфеле – вес одной ценной бумаги в портфеле не отрицателен, и не должен превышать 0,15, это помогло избежать чрезмерной концентрации капитала в отдельных ценных бумагах в результате численного решения задачи оптимизации.

Алгоритм определения веса оптимального портфеля в начале каждого квартала сводится к следующему:

• 1)    производится оценка совместного распределения дневных доходностей акций российских и американских компаний, а также фондовых индексов с использованием различных моделей КПК (R-Vine-MST и R-Vine-INDX). Для оценки моделей распределения используются данные о дневных рублевых доходностях акций и индексов за два года, предшествующих дате формирования портфеля;

  

• 2)    генерируется W = 10 000 независимых наблюдений дневных доходностей акций и индексов с использованием оценок моделей совместного распределения;

• 3)    методом множителей Лагранжа рассчитываются веса портфелей, при которых достигается максимум (минимум) целевых функций ³ .

Накопленный доход, полученный с использованием различных моделей КПК, представлен на рис. 2.

Как видно из графика, модель КПК с первым деревом, структурированным по отраслевому и страновому принципу, продемонстрировала больший прирост капитала для двух задач оптимизации. Прирост капитала за весь период тестирования различных способов формирования структуры представлен в табл. 2.

Примечательно, что использование критерия минимума ожидаемых потерь позволило получить больший прирост капитала по итогам тестирования моделей оптимизации портфеля, в сравнении с критерием максимума коэффициента Шарпа.

Обсуждение и выводы

Результаты тестирования предлагаемого метода структурирования модели КПК по отраслевому и страновому принципу с использованием фондового индекса, в сравнении с традиционным методом максимального остовного дерева, показали, что первый метод позволяет получить больший прирост капитала в рамках решения задачи оптимизации портфеля. Правильные ветвления, первое дерево которых структурировано с использованием фондовых индексов в большей степени напоминают традиционную CAPM, где ожидаемая до-

оо С' С' С' О О О' —   —  — г i е i е i r^, r^, г^, ^т ^т ^т ir, ir, ir. o o o оооо^^^^^^^^^^^^^^^^^^^^^

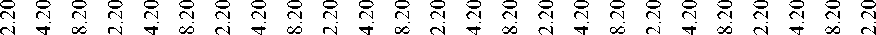
ОО^НОО^ОО^ОО^ОО^ОО^ОО^НОО ооооооооооооооооооооооооо

min CVaR,95% (R-Vine-INDX) min CVaR,95% (R-Vine-MST) max Sharp (R-Vine-INDX) max Sharp (R-Vine-MST)

Рис. 2. Динамика накопленного дохода (с учетом реинвестирования) для различных способов формирования портфеля и различных способов структурирования КПК. Рассчитано автором.

Примечания к рисунку: max Sharp – максимизация коэффициента Шарпа, min CVaR – минимизация показателя ожидаемых потерь в 5 % наихудших случаях

Прирост капитала при разных методах формирования портфеля, %

Таблица 2

Критерии оптимизации Используемые методы R-Vine-INDX R-Vine-MST Минимизация уровня ожидаемых потерь (CVaR, 95%) 615 561 Максимизация коэффициента Шарпа 515 486 ходность актива моделируется относительно рыночного портфеля. По нашему мнению, введение в модель фондовых индексов позволяет выделить систематический риск ценных бумаг, снизить влияние временных ложных корреляций на принимаемые инвестиционные решения. Особую цен- ность предлагаемый в статье метод структурирования моделей КПК может представлять при осуществлении международной диверсификации портфеля.

«Финансы, денежное обращение и кредит» ЮУрГУ за помощь в редактировании текста статьи. Автор также благодарен профессору Даниловой Ирине Валентиновне (ВШЭУ ЮУрГУ) за конструктивную критику и четкое разъяснение требований журнала к научным публикациям.