Моделирование дозвуковых многокомпонентных реагирующих газовых потоков на неструктурированных сетках
Автор: Жалнин Руслан Викторович, Масягин Виктор Федорович, Пескова Елизавета Евгеньевна, Тишкин Владимир Федорович
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Физико-математические науки
Статья в выпуске: 1, 2020 года.
Бесплатный доступ
Введение. В работе проведено моделирование задачи о дозвуковом течении газа в проточном химическом реакторе. Численный алгоритм основан на методе конечных объемов, расчет проведен на неструктурированных треугольных сетках с использованием технологии параллельных вычислении Message Passing Interface (MPI). Материалы и методы. Для описания исследуемых течений многокомпонентного химически активного газа приняты в рассмотрение уравнения Навье - Стокса в приближении малых чисел Маха. Для решения данных уравнений используется метод конечных объемов на неструктурированных треугольных сетках. В работе применяется схема расщепления по физическим процессам, а именно: сначала решаются уравнения химической кинетики, отвечающие за превращения веществ, а затем ищется решение уравнений, описывающих законы сохранения импульса и энергии для каждой компоненты газовой смеси. Для нахождения численных потоков через ребра элементов сетки используется схема Лакса - Фридрихса - Русанова. Для решения уравнений химической кинетики применен алгоритм, предложенный коллективом под руководством Н. Н. Калиткина. Для разделения сетки на связные подобласти с примерно равным количеством ячеек используется библиотека METIS. Для организации параллельных вычислений применяется MPI. Результаты исследования. В статье представлены результаты моделирования течения многокомпонентного газа с учетом эффектов вязкости, диффузии, теплопроводности и химических реакций на неструктурированных треугольных сетках, а именно: было проведено численное моделирование течения дозвукового газа в проточном химическом реакторе на примере пиролиза этана, проведено сравнение полученных результатов с результатами эксперимента и известными численными решениями данной задачи. Обсуждение и заключение. Полученные в работе результаты по конверсии исходной газовой смеси хорошо согласуются с известными экспериментальными данными. Представленные картины распределения основных компонент смеси и газодинамические параметры соответствуют картине течения, наблюдаемой экспериментально. Дальнейшая работа в данном направлении предполагает моделирование дозвуковых газовых течений на неструктурированных тетраэдральных сетках с использованием алгоритмов повышенного порядка точности для исследования протекающих процессов.
Уравнения навье - стокса, дозвуковые течения, малые числа маха, химическая кинетика, пиролиз этана, неструктурированные треугольные сетки
Короткий адрес: https://sciup.org/147220645
IDR: 147220645 | УДК: 519.63:533.6.011.72 | DOI: 10.15507/2658-4123.030.202001.162-175
Текст научной статьи Моделирование дозвуковых многокомпонентных реагирующих газовых потоков на неструктурированных сетках
Введение. В работе проведено моделирование задачи о дозвуковом течении газа в проточном химическом реакторе. Численный алгоритм основан на методе конечных объемов, расчет проведен на неструктурированных треугольных сетках с использованием технологии параллельных вычислении Message Passing Interface (MPI). Материалы и методы. Для описания исследуемых течений многокомпонентного химически активного газа приняты в рассмотрение уравнения Навье – Стокса в приближении малых чисел Маха. Для решения данных уравнений используется метод конечных объемов на неструктурированных треугольных сетках. В работе применяется схема расщепления по физическим процессам, а именно: сначала решаются уравнения химической кинетики, отвечающие за превращения веществ, а затем ищется решение уравнений, описывающих законы сохранения импульса и энергии для каждой компоненты газовой смеси. Для нахождения численных потоков через ребра элементов сетки используется схема Лакса – Фридрихса – Русанова. Для решения уравнений химической кинетики применен алгоритм, предложенный коллективом под руководством Н. Н. Калиткина. Для разделения сетки на связные подобласти с примерно равным количеством ячеек используется библиотека METIS. Для организации параллельных вычислений применяется MPI.
Результаты исследования. В статье представлены результаты моделирования течения многокомпонентного газа с учетом эффектов вязкости, диффузии, теплопроводности и химических реакций на неструктурированных треугольных сетках, а именно: было проведено численное моделирование течения дозвукового газа в проточном химическом реакторе на примере пиролиза этана, проведено сравнение полученных результатов с результатами эксперимента и известными численными решениями данной задачи.
Обсуждение и заключение. Полученные в работе результаты по конверсии исходной газовой смеси хорошо согласуются с известными экспериментальными данными. Представленные картины распределения основных компонент смеси и газодинамические параметры соответствуют картине течения, наблюдаемой экспериментально. Дальнейшая работа в данном направлении предполагает моделирование дозвуковых газовых течений на неструктурированных тетраэдральных сетках с использованием алгоритмов повышенного порядка точности для исследования протекающих процессов.
|(«) ® 1 Контент доступен по лицензии Creative Commons Attribution 4.0 License.
This work is licensed under a Creative Commons Attribution 4.0 License.
Финансирование: Работа выполнена при поддержке Министерства науки и высшего образования РФ (№ 1.6958.2017/8.9), ФГБУ «Российский фонд фундаментальных исследований» (проект № 18-31-00102) и гранта Президента РФ для молодых российских ученых – кандидатов наук (МК-2007.2018.1).
Modeling the Flow of Multicomponent Reactive Gas on Unstructured Grids
R. V. Zhalnina*, V. F. Masyagina, E. E. Peskovaa,V. F. Tishkinb
aNational Research Mordovia State University (Saransk, Russia) bKeldysh Institute of Applied Mathematics of Russian Academy of Sciences (Moscow, Russia)
-
* zhrv@mrsu.ru
Introduction. The article deals with mathematical modeling of the subsonic flow of a multicomponent reactive mixture in a flowing chemical reactor. The numerical algorithm is based on the finite volume method; the calculation is performed on unstructured triangular grids using the Message Passing Interface parallel computing technology.
Materials and Methods . To describe the flows under studying, the Navier–Stokes equations are used in the approximation for low Mach numbers. To solve these equations, the finite volume method on unstructured triangular grids is used. The study uses a splitting scheme for physical processes, namely, the chemical kinetics equations responsible for the transformations of substances are first solved, and then the equations describing the conservation laws of momentum and energy for each component of the gas mixture are solved. To find numerical flows through the edges of the grid elements, the Lax–Fried-richs–Rusanov scheme is used. To solve the equations of chemical kinetics, a compact algorithm proposed by the team led by N.N. Kalitkin is used. The METIS library is used to divide the grid into connected subdomains with an approximately equal number of cells. To organize parallel computing, Message Passing Interface technology is used.
Results. The article presents a numerical algorithm for studying multicomponent gas flows on unstructured triangular grids taking into account viscosity, diffusion, thermal conductivity, and chemical reactions. As a result of the study, a numerical simulation of the flow of a subsonic multicomponent gas in a flowing chemical reactor was carried out using ethane pyrolysis as an example. Computational, known numerical solutions and experimental data of ethane pyrolysis in a flowing reactor are compared.
Discussion and Conclusion. The numerical results on the conversion of the initial gas mixture are in good agreement with the known experimental data. The presented distribution patterns of the main components of the mixture and gas-dynamic parameters correspond to the flow pattern observed experimentally. Further work in this direction involves the modeling of subsonic gas flows on unstructured tetrahedral meshes using algorithms of higher accuracy for a more accurate study of ongoing processes.
В настоящее время для исследования газовых течений активно применяется математическое моделирование [1–3]. Так, в задачах нефтехимической промышленности перед технологами стоит цель проведения реакции с максимальным выходом целевых продуктов, для ее достижения необходимо выбрать оптимальные значения температуры проведения реакции, состава и расхода исходной газовой смеси и других параметров. Проведение натурных экспериментов зачастую является трудоемкой и дорогостоящей процедурой, поэтому целесообразно пользоваться средствами математического моделирования.
При исследовании множества химических процессов приходится сталкиваться с низкоскоростными течениями, что приводит к необходимости выбора соответствующей математической модели. К тому же исследование реальных течений газовых смесей приходится проводить в областях сложной геометрической формы, в связи с чем возникает необходимость в использовании неструктурированных сеток. Нужно отметить, что численные алгоритмы решения задач исследования газовых течений очень требовательны к ресурсам вычислительной техники (необходимо учитывать процессы теплообмена, диффузии, химических превращений, использовать детальные кинетические схемы, которые могут включать сотни элементарных стадий). В этой связи целесообразно использовать средства параллельного программирования на суперкомпьютерах. Таким образом, в настоящей работе стоит задача моделирования многокомпонентных реагирующих потоков газа в проточных реакторах на неструктурированной треугольной сетке с применением суперкомпьютерных технологий. Было проведено сравнение численных результатов по конверсии исходной газовой смеси на выходе из реактора с экспериментальными данными и данными, полученными в ходе других вычислительных экспериментов.
Обзор литературы
Во многих областях современной науки рассматриваются многокомпонентные течения газовых смесей с протекающими в них химическими реакциями. С такими течениями можно встретиться, например, при исследовании процессов горения, процессов в нефтехимической промышленности, газодинамике лазеров и катализаторов.
При исследовании реагирующих течений зачастую встречаются низкоскоростные газовые потоки, при моделировании которых приходится сталкиваться с вычислительными трудностями, связанными с неоправданно малым шагом интегрирования по времени и незначительным изменением давления в об-ласти1. В работах ряда исследователей предложено множество подходов к решению данных проблем [4–7]. Описан метод проекций, в ходе реализации которого было проведено интегрирование законов сохранения массы, импульса и энергии, используя начальное поле давления [5; 8–10]. Таким образом были получены значения концентраций веществ, температуры и плотности газовой смеси, предварительное поле скорости. Затем с учетом найденных величин находились давление и поправки к вектору скорости.
Для численного моделирования химически реагирующих потоков приходится решать жесткие системы уравнений, описывающие химические превращения веществ. Использование явных схем интегрирования не всегда возможно для решения данных задач. Для решения жестких систем обыкновенных дифференциальных уравнений широко применяются неявные многошаговые методы Гира [11], схемы Ро-зенброка [12], которые обладают высокой трудоемкостью. В одной из работ Н. Н. Калиткиным и В. Я. Гольдиным была предложена явная схема первого порядка точности, основанная на специфическом виде задач химической кинетики, в другом исследовании разработана схема второго порядка точности [13; 14].
Расчеты реальных газодинамических течений с учетом химических превращений являются ресурсоемкими, поэтому их практическое использование сложно представить без использования технологий параллельных вычислений. Применение технологий параллельных вычислений дает возможность разработать программные средства для исследования газодинамических течений на основе схем высокого порядка точности и провести вычисления на неструктурированных сетках большого объема с детальным описанием механизмов химических превращений [15; 16].
Данная работа посвящена математическому моделированию низкоскоростного течения газа с учетом процессов вязкости, теплопроводности и химических превращений. В работе проводится сравнение численных результатов с известными экспериментальными и численными данными.
Материалы и методы
Рассмотрим систему уравнений Навье – Стокса в приближении малых чисел Маха [4; 5; 10]:
^pY = -V-( p^v )-V. j+ q, о t
d(pv) , =
= -V-( pvv )-Vn + V-t, dt
"^ph) = v'( Ph )-V' ?•
Уравнение состояния и условие на дивергенцию вектора скорости:
( P p. = PRT Цтг
i V Mwi /
,
5 = V- v
1 CP?
V- XV T + ^ p D m V Y i V h i 1 +
+ P^^ M w- PD V Y )+
+1 s p i
Г M w
M . у Wi
■ i ,
где Yi – массовая доля i -й компоненты; Mwi – молекулярная масса i -й компоненты; ρ – плотность смеси; h – энтальпия смеси; T - температура; v - вектор скорости; π = p ‒ p 0 – динамическая составляющая давления; p 0 – термодинамическая составляющая да в ления; т- тензор вязких напряжений; Ji – вектор диффузионного потока; - вектор потока тепла смеси; Q i – скорость образования или расхода i -й компоненты.
Вектор диффузионного потока i -й компоненты и вектор потока тепла для смеси определяем с использованием модели средних по смеси значений [10]:
I
J i =- ρ D im ∇ Y i
q = -XV т—^hipDm у y , г где Dim – средний по смеси коэффициент диффузии i-й компоненты; λ – коэф- фициент теплопроводности смеси; hi -энтальпия i-й компоненты:
T h = S СД T) dT + hi,
T где h0 - энтальпия образования i-й компоненты при стандартной температуре T0 = 298,15 K; Cpi - удельная теплоемкость i-й компоненты при постоянном давлении.
Для определения тензора вязких напряжений используем следующее выражение:
= И
V v + ( V v )Т
) - 3 h ( v- v ) I ,
где I – единичный тензор; μ – коэффициент динамической вязкости.
Скорость образования или расхода i -й компоненты газовой смеси определяем следующим образом:
Q. = M . V y. w , iwi in n ,
n где vin - стехиометрические коэффициенты i-й компоненты в стадии реакции n; wn - скорость i-й стадии.
Для построения дискретной модели вводим неструктурированную сетку:
to = { P k = ( X k , y k ) , k = 1,..., K } .
После чего строим на ней триангуляцию Делоне:
А ( ю ) =
= { a„=a ( p ,p ,p ) , P , p ,p G ® , m = 1... M } . mmm mmm
Газодинамические параметры и массовые доли компонент газовой смеси рассматриваем как интегральные средние в ячейках сетки.
При решении уравнений Навье – Стокса изменение концентраций компонентов газовой смеси за счет хи- мических превращений учитываем с использованием следующей системы уравнений [10]:
dP Y d t
= Q i ,
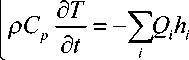
где i = 1,..., M - количество компонентов газовой смеси и, соответственно, количество уравнений, описывающих химические превращения веществ, которые можно представить в виде [14]:
d^ = - cM c ) + V i ( c ) , c = ( c i , c 2, _ , C m ) ,
PY где сг. = i , причем c, > 0, ф,(c) > 0, i Mwi
Vr ( c ) > 0.
Используя специализированную явную схему второго порядка точности [14], решение системы уравнений химической кинетики находим простыми итерациями:
A s + 1
c i
c i + тф( ( c s ) ( 1 + T^f
( c s ) /
1 + TV i
2 ,
( c ) + ( T^ i ( c ) ) /2
∧ c + c
c s
A 0 c
= c ,
где с , - решение в исходный момент времени; c - решение в новый момент времени. Для решения системы необходимо выполнить только две итерации, последующие итерации выполнять не следует: они не повышают порядок точности и ухудшают надежность схемы [14].
Систему уравнений Навье – Стокса с учетом решенных уравнений хими- ческой кинетики можно представить в следующем векторном виде:
д U + d ( F 1 ( U ) - H 1 ( U , v U ) ) + д t д x
/( F 2 ( U ) - H 2 ( U , v U ) ) = 0
8 y
Вектор консервативных переменных U и векторы конвективных и диффузионных потоков F 1,2( U ), H 1,2 ( U , V U ) , заданы в виде:
|
< p Y i |
^ p uY i |
^ p vY , |
|||
|
U = |
p u |
, F ( 1 )( U ) = |
p u 2 |
, F ( 2 )( U ) = |
p uv |
|
p v |
p uv |
p v 2 |
|||
|
V p h 7 |
V p hu 7 |
v p hv 7 |
|
J ix |
iy |
||
|
H ( 1 )( U , V U ) = |
T xx T xy |
, H ( 2 )( U , V U ) = |
T yx T yy |
|
. q x > |
l. q y J |
∂ Y ∂ Y
J ix = ρ D mi i , J iy = ρ D mi i ,
∂x ∂y qx
q y
d T M d Y j
= X--+ > h.pD . —-, dx £ jP mj dx d T M d Y
= X --+ > h.pD . —-, d y £ j p mj d y ,
Cdu 2 (du dv т„ = Д 2---— + — , xx
( хл ( c/ x У.У J у
_ f dv 2 fdu vv Y т = Щ 21, yy M( dy 3(dx dyJJ где i = 1, 2,..., M; M - количество элементов в реагирующей смеси.
Для построения разностной схемы проинтегрируем по ячейке A m , ограниченной поверхностью ∂Δ m , и, используя формулу Гаусса - Остроградского, получим следующее выражение:
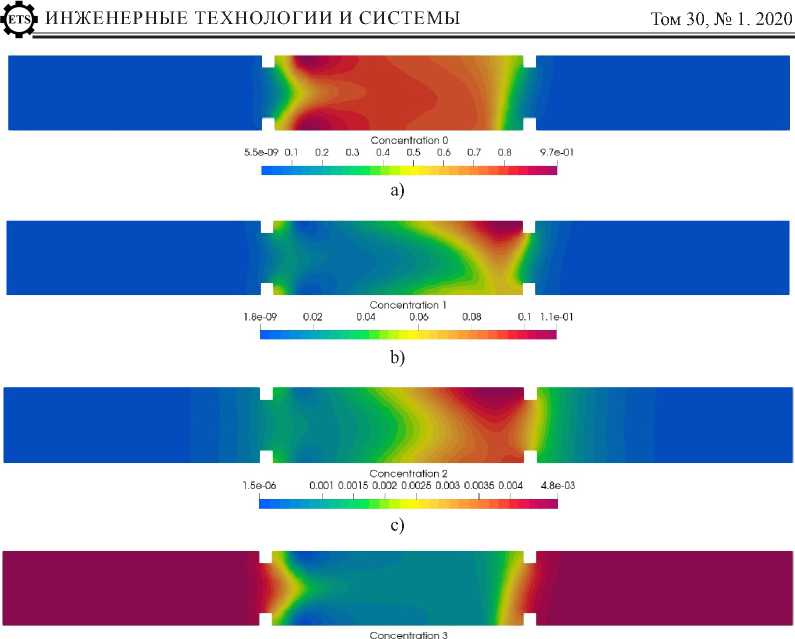
— JUdS + + ф (F2 (U)- H2(U, V U ))nydl = 0, 5A m где n = (nx, ny) - внешняя нормаль к границе ячейки. При интегрировании в качестве среднего значения на грани принимаем значение в центре грани, в качестве среднего значения по объему – значение в центре ячейки. Тогда уравнение для ячейки запишем следующим образом: 8yS*.+£ (F? 1( u )-/J1 ( u ,v u ))"-'-+ +£( F-2(U)-Й2(U, V U)) nyle = 0, e=1 где le - длина грани; F1(U) = F1(U1, Ur), F?2(U ) = F2(U, Ur) - конвективные потоки на границе ячейки, которые рассчитываем по схеме Лакса – Фридрихса - Русанова; Й1(U, V U), HI2(U, VU) - диффузионные и тепловые потоки на границе ячейки, которые рассчитываем по схеме с центральными разностями [16–18]. Вычисленное предварительное поле скорости V* не удовлетворяет условию на дивергенцию скорости S [10]. Для его коррекции используем следующее выражение: xy = Tyx (dv du = Ц\1Т + 1^, (dx dy J V V* At v = v--Vn. ρ Для нахождения динамической составляющей давления решаем уравнение Пуассона: V--1 Vn = — (v-V* ρ ∆t -S). Построение параллельного вычислительного алгоритма основано на технологии для систем с распределенной памятью Message Passing Interface (MPI). Используя пакет METIS, было проведено геометрическое разбиение расчетной области на подобласти, количество которых равно количеству используемых процессоров (рис.1). В каждой области с использованием описанной численной схемы проводим расчет газодинамических параметров и концентраций веществ. Учитывая особенность построения вычислительного алгоритма, на каждой из подобластей дополнительно хранится информация о соседних ячейках (соседей по ребру), расчет в которых ведется на другом процессоре. Для определения граничных условий между соседними подобластями организован межпроцессорный обмен, для которого используем стандартные методы библиотеки Message Passing Interface CHameleon (MPICH), а именно парные блокирующие функции MPI_Send() и MPI _Recv(). Выбор данных функций обусловлен наличием обменов только между соседними подобластями. Каждый процессор выводит результаты расчетов в файлы XML-формата (VTU, PVTU). Визуализацию численных данных осуществляем с использованием открытого пакета Para View. В результатах серии исследований представлена установка, предназначенная для термического пиролиза углеводородов [19–22]. Также исследуются результаты численного моделирования процесса термического пиролиза этана и проведено сравнение с результатами эксперимента [19; 23; 24]. Сравнение данных, полученных экспериментально, и результатов расчетов выполнено на основе сравнения конверсии исходной газовой смеси. Для расчетов, описанных О. А. Стадниченко и соавторами, был использован пакет Ansys Fluent, в статье Р. В. Жалнина и коллег численный алгоритм построен на основе метода конечных объемов на прямоугольной сетке с использованием Weighted Essentially Non-Oscillatory (WENO) схем пятого порядка точности [19; 23; 25]. Результаты, приведенные в данных работах, хорошо согласуются с экспериментальными данными. Для моделирования процесса термического разложения этана в реакторе с внешним обогревом зоны реакции была принята следующая физическая постановка задачи [19-22]. В начальный момент времени реактор заполнен метаном, температура в области 300 К, давление 101 325 Па. В буферную зону подается метан с температурой 300 К и расходом 0,316 мг⁄с. В реакционную зону подается этан, температура которого 600 К, расход 0,754 мг⁄с. Температура торцевых стенок 300 К, нагревательных элементов 973 К, температура корпуса в буферных зонах меняется по линейному закону от 300 К у торцевых стенок до 973 К на границе с реакционной зоной. Р и с. 1. Декомпозиция расчетной области F i g. 1. Decomposition of the computational domain 168 Физико-математические науки На рисунке 2 представлены распределения массовых долей основных компонент смеси: этана, этилена, водорода, метана. Из рисунков 2b, 2c видно, что концентрация целевых продуктов пиролиза, этилена и водорода, наблюдается в правой части зоны реакции и у нагревательных элементов, так как именно в этих областях температура газа (рис. 3) максимальна и, следовательно, химические превращения происходят наиболее интенсивно. Доля защитного газа метана (рис. 2d) максимальна в буферных зонах за счет постоянной его подачи через соответствующие вводы. Максимальная плотность (рис. 4) наблюдается в областях подачи газовой смеси и у торцевых стенок, так как газ по своим характеристикам близок к идеальному, и температура его в этих областях минимальна. В таблице 1 представлена зависимость конверсии исходной газовой смеси, подаваемой в реакционную зону, от температуры нагревательных элементов. Можно сделать вывод о хорошем соответствии экспериментальных данных, ранее полученных результатов на структурированной прямоугольной сетке с использованием алгоритмов повышенного порядка точности [23] и результатов текущих расчетов. Из таблицы 1 видно, что при самой низкой и самой высокой температуре результаты текущего расчета на неструктури- рованной сетке дают завышенный результат по конверсии. Такое поведение можно объяснить первым порядком точности используемой численной схемы и погрешностью, которую вносит в схему использование неструктурированной сетки. Для достижения лучших численных результатов по исследованию газового потока с указанными начальными и граничными условиями необходимо уточнение геометрии реактора и использование в расчетах схем повышенного порядка точности. Обсуждение и заключение В работе проведено математическое моделирование динамики дозвукового многокомпонентного химически реагирующего газа на неструктурированных треугольных сетках с учетом процессов вязкости, диффузии и теплопроводности. Разработан параллельный вычислительный алгоритм и комплекс программ на его основе с использованием технологии MPI для моделирования течения газа в проточном химическом реакторе с внешним обогревом стенок. Проведено тестирование разработанного программного комплекса на задаче, описывающей процесс термического разложения этана. Результаты, полученные в ходе сравнения расчетных и экспериментальных данных, показали хорошее соответствие. Картины распределения основных компонент газовой смеси и газодинамических па- Т а б л и ц а 1 T a b l e 1 Сравнение расчетных и экспериментальных данных конверсии этана Comparison of calculated and experimental conversion of ethane Температура, К / Temperature, K Эксперимент, % / Experiment, % Расчет на прямоугольной сетке, % / Calculation on a rectangular grid, % Текущий расчет, % / Current calculation,% 915 2,10 1,97 7,20 973 15,60 14,28 15,24 1 015 37,00 35,15 35,27 1 033 48,78 48,15 51,73 2.5е-02 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0е+00 d) Р и с. 2. Распределение массовых долей: а) этан; b) этилен; c) водород; d) метан F i g. 2. Distribution of the mass fraction: a) ethane; b) ethylene; c) hydrogen; d) methane Temperature 3.0e+02 400 500 600 700 800 900 9.7e+02 ^^^^— 1 =^^^— Р и с. 3. Температура F i g. 3. Temperature Р и с. 4. Плотность F i g. 4. Density раметров согласуются с основными физико-химическими законами, протекающими в ходе термического пиролиза углеводородов в химическом реакторе. Для более точного анализа исследуемых процессов в дальнейшем плани- руется уточнение геометрии реактора, а именно предполагается исследование трехмерной модели реактора с использованием неструктурированных тетраэдральных сеток и алгоритмов повышенного порядка аппроксимации. 1. Бондарев, А. Е. Численное моделирование низкоскоростных течений на примере энергоустановки с использованием комплекса NOISEtte / А. Е. Бондарев, В. А. Галактионов, В. Т. Жуков [и др.]. – DOI 10.20948/prepr-2018-224 // Препринты ИПМ им. М. В. Келдыша. – 2018. – № 224. – 20 с. URL: https://library.keldysh.ru/preprint.asp?id=2018-224 (дата обращения: 25.02.2020). 2. Кулешов, А. А. Алгоритм численного решения для двумерной трехфазной модели лесных пожаров / А. А. Кулешов, Е. Е. Мышецкая – DOI 10.20948/prepr-2018-202 // Препринты ИПМ им. М. В. Келдыша. – 2018. – № 202. – 16 с. URL: https://library.keldysh.ru/preprint.asp?id=2018-202 (дата обращения: 25.02.2020). 3. Abalakin, I. V. Implementation of the Low Mach Number Method for Calculating Flows in the NOISEtte Software Package / I. V. Abalakin, V. G. Bobkov, T. K. Kozubskaya. – DOI 10.1134/ S2070048217060023 // Mathematical Models and Computer Simulations. – 2017. – Vol. 9. – Pp. 688–696. URL: https://link.springer.com/article/10.1134%2FS2070048217060023#citeas (дата обращения: 25.02.2020). 4. Almgren, A. S. A Conservative Adaptive Projection Method for the Variable Density Incompressible Navier – Stokes Equations / A. S. Almgren, J. B. Bell, P. Colella [et al.]. – DOI 10.1006/jcph.1998.5890 // Journal of Computational Physics. – 1998. – Vol. 142, issue 1. – Pp. 1–46. URL: https://www.sciencedirect.com/ science/article/pii/S0021999198958909?via%3Dihub (дата обращения: 25.02.2020). 5. Day, M. S. Numerical Simulation of Laminar Reacting Flows with Complex Chemistry / M. S. Day, J. B. Bell. – DOI 10.1088/1364-7830/4/4/309 // Combustion Theory and Modelling. – 2000. – Vol. 4, issue 4. – Pp. 535–556. URL: https://www.tandfonline.com/doi/abs/10.1088/1364-7830/4/4/309 (дата обращения: 25.02.2020). 6. Metzner, M. Computing Low Mach Number Flows by Parallel Adaptive Multigrid / M. Metzner, G. Wittum. – DOI 10.1007/s00791-006-0025-x // Computing and Visualization in Science. – 2006. – Vol. 9, issue 4. – Pp. 259–269. URL: https://link.springer.com/article/10.1007%2Fs00791-006-0025-x#citeas (дата обращения: 25.02.2020). 7. Turkel, E. Assessment of Preconditioning Methods for Multidimensional Aerodynamics / E. Turkel, R. Radespiel, N. Kroll. – DOI 10.1016/S0045-7930(97)00013-3 // Computers & Fluids. – 1997. – Vol. 26, issue 6. – Pp. 613–634. URL: https://www.sciencedirect.com/science/article/abs/pii/ S0045793097000133?via%3Dihub (дата обращения: 25.02.2020). 8. Almgren, A. S. A Numerical Method for the Incompressible Navier – Stokes Equations Based on an Approximate Projection / A. S. Almgren, J. B. Bell, W. G. Szymczak. – DOI 10.1137/ S1064827593244213 // SIAM Journal on Scientific Computing. – 1996. – Vol. 17, issue 2. – Pp. 358–369. URL: https://epubs.siam.org/doi/10.1137/S1064827593244213 (дата обращения: 25.02.2020). 9. Bell, J. B. A Second-Order Projection Method for the Incompressible Navier – Stokes Equations / J. B. Bell, P. Colella, H. M. Glaz. – DOI 10.1016/0021-9991(89)90151-4 // Journal of Computational Physics. – 1989. – Vol. 85, issue 2. – Pp. 257–283. URL: https://www.sciencedirect.com/science/article/ pii/0021999189901514?via%3Dihub (дата обращения: 25.02.2020). 10. Борисов, В. Е. Применение адаптивных иерархических сеток для расчета течений реагирующих газов / В. Е. Борисов, С. Е. Якуш // Физико-химическая кинетика в газовой динамике. – 2015. – Т. 16, вып. 2. – 13 с. URL: http://chemphys.edu.ru/issues/2015-16-2/articles/544/ (дата обращения: 25.02.2020). – Рез. англ. 11. Gear, W. C. Numerical Initial Value Problems in Ordinary Differential Equations / W. C. Gear. – New Jersey : Prentice Hall, 1971. – 253 p. 12. Rosenbrock, H. H. Some General Implicit Processes for the Numerical Solution of Differential Equations / H. H. Rosenbrock. – DOI 10.1093/comjnl/5.4.329 // The Computer Journal. – 1963. – Vol. 5, issue 4. – Pp. 329–330. URL: https://academic.oup.com/comjnl/article/5/4/329/316388 (дата обращения: 25.02.2020). 13. Goldin, V. Ya. Finding the Solutions of Constant Sign of Ordinary Differential Equations / V. Ya. Goldin, N. N. Kalitkin. – DOI 10.1016/0041-5553(66)90044-9 // USSR Computational Mathematics and Mathematical Physics. – 1966. – Vol. 6, issue 1. – Pp. 228–230. URL: https://www.sciencedirect.com/ science/article/abs/pii/0041555366900449?via%3Dihub (дата обращения: 25.02.2020). 14. Belov, A. A. Modeling of Chemical Kinetics in Gases / A. A. Belov, N. N. Kalitkin, L. V. Kuzmina. – DOI 10.1134/S2070048217010057 // Mathematical Models and Computer Simulations. – 2017. – Vol. 9. - Pp. 24-39. URL: https://link.springer.com/article/10.1134%2FS2070048217010057 (дата обращения: 25.02.2020). 15. Горобец, А. В. Производительность отечественного процессора Эльбрус-8С в суперкомпьютерном моделировании задач вычислительной газовой динамики / А. В. Горобец, М. И. Нейман-заде, С. К. Окунев [и др.]. – DOI 10.1134/S0234087919040026 // Математическое моделирование. – 2019. – Т. 31, № 4. – C. 17–32. URL: https://www.elibrary.ru/item.asp?id=37242382 (дата обращения: 25.02.2020). – Рез. англ. 16. Lyupa, A. A. Simulation of Oil Recovery Processes with the Employment of High-Performance Computing Systems / A. A. Lyupa, D. N. Morozov, M. A. Trapeznikova [et al.]. – DOI 10.1134/ S2070048216020095 // Mathematical Models and Computer Simulations. – 2016. – Vol. 8. – Pp. 129–134. URL: https://link.springer.com/article/10.1134%2FS2070048216020095#citeas (дата обращения: 25.02.2020). 17. Rusanov, V. V. The Calculation of the Interaction of Non-Stationary Shock Waves and Obstacles / V. V. Rusanov. - DOI 10.1016/0041-5553(62)90062-9 // USSR Computational Mathematics and Mathematical Physics. – 1962. – Vol. 1, issue 2. – Pp. 304–320. URL: https://www.sciencedirect.com/science/ article/abs/pii/0041555362900629?via%3Dihub (дата обращения: 25.02.2020). 18. Lax, P. D. Weak Solutions of Nonlinear Hyperbolic Equations and Their Numerical Computation / P D. Lax. - DOI 10.1002/Cpa.3160070112 // Communications on Pure and Applied Mathematics. – 1954. – Vol. 7, issue 1. – Pp. 159–193. URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/ cpa.3160070112 (дата обращения: 25.02.2020). 19. Стадниченко, О. А. Математическое моделирование потоков многокомпонентного газа с энергоемкими химическими процессами на примере пиролиза этана / О. А. Стадниченко, В. Н. Снытников, В. Н. Снытников // Вычислительные методы и программирование: новые вычислительные технологии. – 2014. – Т. 15. – С. 658–668. – Рез. англ. 20. Snytnikov, V. N. Autocatalytic Gas-Phase Dehydrogenation of Ethane / V. N. Snytnikov, T. I. Mishchenko, V. N. Snytnikov. – DOI 10.1007/s11164-011-0449-x // Research on Chemical Intermediates. – 2012. – Vol. 38, issue 3. – Pp. 1133–1147. URL: https://link.springer.com/article/10.1007%2Fs11164-011-0449-x (дата обращения: 25.02.2020). 21. Stadnichenko, O. A. Mathematical Modeling of Ethane Pyrolysis in a Flow Reactor with Allowance for Laser Radiation Effects / O. A. Stadnichenko, V. N. Snytnikov, V. N. Snytnikov. – DOI 10.1016/j.cherd.2016.02.008 // Chemical Engineering Research and Design. – 2016. – Vol. 109. – Pp. 405–413. URL: https://www.sciencedirect.com/science/article/abs/pii/S026387621600071X?via%3D ihub(дата обращения: 25.02.2020). 22. Masyuk, N. Effect of Infrared Laser Radiation on Gas-Phase Pyrolysis of Ethane / N. Masyuk, A. Sherin, V. N. Snytnikov [et al.]. – DOI 10.1016/j.jaap.2018.05.017 // Journal of Analytical and Applied Pyrolysis. – 2018. – Vol. 134. – Pp. 122–129. URL: https://www.sciencedirect.com/science/article/pii/ S0165237017305594?via%3Dihub (дата обращения: 25.02.2020). 23. Жалнин, Р. В. Моделирование течения многокомпонентного реагирующего газа с использованием алгоритмов высокого порядка точности / Р. В. Жалнин, Е. Е. Пескова, О. А. Стадниченко [и др.]. - DOI 10.20537/vm170410 // Вестник Удмуртского университета. Математика. Механика. Компьютерные науки. – 2017. – Т. 27, № 4. – С. 608–617. URL: http://www.mathnet.ru/php/archive.pht ml?wshow=paper&jrnid=vuu&paperid=612&option_lang=eng (дата обращения: 25.02.2020). 24. Жалнин, Р. В. Моделирование течения многокомпонентного химически активного газа на примере пиролиза углеводородов / Р. В. Жалнин, Е. Е. Пескова, О. А. Стадниченко [и др.]. – DOI 10.20948/prepr-2017-101 // Препринты ИПМ им. М. В. Келдыша. – 2017. – № 101. – 16 с. URL: http:// library.keldysh.ru/preprint.asp?id=2017-101 (дата обращения: 25.02.2020). 25. Shu, C.-W. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws / C.-W. Shu. – DOI 10.1007/BFb0096355 // Advanced Numerical Approximation of Nonlinear Hyperbolic Equations. – 1997. – Vol. 1697. – Pp. 325–432. URL: https:// link.springer.com/chapter/10.1007/BFb0096355#citeas (дата обращения: 25.02.2020). 172 Физико-математические науки Поступила 13.09.2019; принята к публикации 07.11.2019; опубликована онлайн 31.03.2020 Об авторах: Заявленный вклад соавторов: Р. В. Жалнин – разработка методики исследования; В. Ф. Масягин – реализация алгоритма и программного комплекса; Е. Е. Пескова - поиск алгоритма расчетов, проведение исследования полученных численных результатов; В. Ф. Тишкин – постановка задачи и общее руководство работой. Все авторы прочитали и одобрили окончательный вариант рукописи. 1. Bondarev A.E., Galaktionov V.A., Zhukov V.T., et al. Numerical Simulation of Low-Speed Flows Around of Power Plant Using NOISEtte. Preprinty IPM im. M.V. Keldysha = KIAM Preprint. 2018; 224. 20 p. (In Russ.) DOI: https://doi.org/10.20948/prepr-2018-224 2. Kuleshov A.A., Myshetskaya E.E. Numerical Algorithm for Two-Dimensional Three-Phase Mathematical Model of Forest Fires. Preprinty IPM im. M.V. Keldysha = KIAM Preprint. 2018; 202. 16 p. (In Russ.) DOI: https://doi.org/10.20948/prepr-2018-202 3. Abalakin I.V., Bobkov V.G. Kozubskaya T.K. Implementation of the Low Mach Number Method for Calculating Flows in the NOISEtte Software Package. Mathematical Models and Computer Simulations. 2017; 9:688-696. (In Eng.) DOI: https://doi.org/10.1134/S2070048217060023 4. Almgren A.S., Bell J.B., Colella P., et al. A Conservative Adaptive Projection Method for the Variable Density Incompressible Navier – Stokes Equations. Journal of Computational Physics. 1998; 142(1):1-46. (In Eng.) DOI: https://doi.org/10.1006/jcph.1998.5890 5. Day M.S., Bell J.B. Numerical Simulation of Laminar Reacting Flows with Complex Chemistry. Combustion Theory and Modelling. 2000; 4(4):535-556. (In Eng.) DOI: https:// doi.org/10.1088/1364-7830/4/4/309 6. Metzner M., Wittum G. Computing Low Mach Number Flows by Parallel Adaptive Multigrid. Computing and Visualization in Science. 2006; 9(4):259-269. (In Eng.) DOI: https:// doi.org/10.1007/s00791-006-0025-x 7. Turkel E., Radespiel R., Kroll N. Assessment of Preconditioning Methods for Multidimensional Aerodynamics. Computers & Fluids. 1997; 26(6):613-634. (In Eng.) DOI: https:// doi.org/10.1016/S0045-7930(97)00013-3 8. Almgren A.S., Bell J.B., Szymczak W.G. A Numerical Method for the Incompressible Navier – Stokes Equations Based on an Approximate Projection. SIAM Journal on Scientific Computing. 1996; 17(2):358-369. (In Eng.) DOI: https://doi.org/10.1137/S1064827593244213 9. Bell J.B., Colella P., Glaz H.M. A Second-Order Projection Method for the Incompressible Na-vier – Stokes Equations. Journal of Computational Physics. 1989; 85(2):257-283. (In Eng.) DOI: https:// doi.org/10.1016/0021-9991(89)90151-4 10. Borisov V.Ye., Yakush S.Ye. Application of Adaptive Hierarchical Grids to Simulation of Reacting Gas Flows. Fiziko-khimicheskaya kinetika v gazovoy dinamike = Physical-Chemical Kinetics in Gas Dynamics. 2015; 16(2). 13 p. Available at: http://chemphys.edu.ru/issues/2015-16-2/articles/544/ (accessed 25.02.2020). (In Russ.) 11. Gear W.C. Numerical Initial Value Problems in Ordinary Differential Equations. New Jersey: Prentice Hall; 1971. 253 p. (In Eng.) 12. Rosenbrock H.H. Some General Implicit Processes for the Numerical Solution of Differential Equations. The Computer Journal. 1963; 5(4):329-330. (In Eng.) DOI: https://doi.org/10.1093/comjnl/5.4.329 13. Goldin V.Ya., Kalitkin N.N. Finding the Solutions of Constant Sign of Ordinary Differential Equations. USSR Computational Mathematics and Mathematical Physics. 1966; 6(1):228-230. (In Eng.) DOI: https://doi.org/10.1016/0041-5553(66)90044-9 14. Belov A.A., Kalitkin N.N., Kuzmina L.V. Modeling of Chemical Kinetics in Gases. Mathematical Models and Computer Simulations. 2017; 9:24-39. (In Eng.) DOI: https://doi.org/10.1134/ S2070048217010057 15. Gorobets A.V., Neiman-Zade M.I., Okunev S.K., et al. Performance of Elbrus-8C Processor in Supercomputer CFD Simulations. Matematicheskoe modelirovanie = Mathematical Models and Computer Simulations. 2019; 31(4):17-32. (In Russ.) DOI: https://doi.org/10.1134/S0234087919040026 16. Lyupa A.A., Morozov D.N., Trapeznikova M.A., et al. Simulation of Oil Recovery Processes with the Employment of High-Performance Computing Systems. Mathematical Models and Computer Simulations. 2016; 8:129-134. (In Eng.) DOI: https://doi.org/10.1134/S2070048216020095 17. Rusanov V.V. The Calculation of the Interaction of Non-Stationary Shock Waves and Obstacles. USSR Computational Mathematics and Mathematical Physics. 1962; 1(2):304-320. (In Eng.) DOI: https://doi.org/10.1016/0041-5553(62)90062-9 18. Lax P.D. Weak Solutions of Nonlinear Hyperbolic Equations and Their Numerical Computation. Communications on Pure and Applied Mathematics. 1954; 7(1):159-193. (In Eng.) DOI: https://doi.org/10.1002/Cpa.3160070112 19. Stadnichenko O.A., Snytnikov V.N., Snytnikov V.N. Mathematical Modeling of Multicomponent Gas Flows with Energy Intensive Chemical Processes by the Example of Ethane Pyrolysis. Vychislitelnye metody i programmirovanie: novye vychislitelnye tekhnologii = Numerical Methods and Programming. 2014; 15:658-668. (In Russ.) 20. Snytnikov V.N., Mishchenko T.I., Snytnikov V.N. Autocatalytic Gas-Phase Dehydrogenation of Ethane. Research on Chemical Intermediates. 2012; 38(3):1133-1147. (In Eng.) DOI: https:// doi.org/10.1007/s11164-011-0449-x 21. Stadnichenko O.A., Snytnikov V.N., Snytnikov V.N. Mathematical Modeling of Ethane Pyrolysis in a Flow Reactor with Allowance for Laser Radiation Effects. Chemical Engineering Research and Design. 2016; 109:405-413. (In Eng.) DOI: https://doi.org/10.1016/j.cherd.2016.02.008 22. Masyuk N., Sherin A., Snytnikov V.N., et al. Effect of Infrared Laser Radiation on Gas-Phase Pyrolysis of Ethane. Journal of Analytical and Applied Pyrolysis. 2018; 134:122-129. (In Eng.) DOI: https://doi.org/10.1016/j.jaap.2018.05.017 23. Zhalnin R.V., Peskova E.E., Stadnichenko O.A., et al. Modeling the Flow of a Multicomponent Reactive Gas Using High Accuracy Algorithms. Vestnik Udmurtskogo universiteta. Matematika. Mekhan-ika. Kompyuternye nauki = Bulletin of Udmurt University. Mathematics. Mechanics. Computer Science. 2017; 27(4):608-617. Available at: paperid=612&option_lang=eng (accessed 25.02.2020). (In Russ.) 24. Zhalnin R.V., Peskova E.E., Stadnichenko O.A., et al. Modeling the Flow of Multicomponent Reactive Gas by the Example of Hydrocarbons Pyrolysis. Preprinty IPM im. M. V. Keldysha = KIAM Preprint. 2017; 101. 16 p. (In Eng.) DOI: https://doi.org/10.20948/prepr-2017-101 25. Shu C.-W. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws. Advanced Numerical Approximation of Nonlinear Hyperbolic Equations. 1997; 1697:325-432. (In Eng.) DOI: https://doi.org/10.1007/BFb0096355




Список литературы Моделирование дозвуковых многокомпонентных реагирующих газовых потоков на неструктурированных сетках
- Бондарев, А. Е. Численное моделирование низкоскоростньгх течений на примере энергоустановки с использованием комплекса NOISEtte / А. Е. Бондарев, В. А. Галактионов, В. Т. Жуков [и др.]. - // Препринты ИПМ им. М. В. Келдыша. - 2018. - № 224. -20 с. URL: https://library.keldysh.ru/preprint.asp?id=2018-224 (дата обращения: 25.02.2020). DOI: 10.20948/prepr-2018-224
- Кулешов, А. А. Алгоритм численного решения для двумерной трехфазной модели лесных пожаров / А. А. Кулешов, Е. Е. Мышецкая - // Препринты ИПМ им. М. В. Келдыша. - 2018. - № 202. - 16 с. URL: https://library.keldysh.ru/preprint.asp?id=2018-202 (дата обращения: 25.02.2020). DOI: 10.20948/prepr-2018-202
- Abalakin, I. V. Implementation of the Low Mach Number Method for Calculating Flows in the NOISEtte Software Package / I. V. Abalakin, V. G. Bobkov, T. K. Kozubskaya. - 10.1134/ S2070048217060023 // Mathematical Models and Computer Simulations. - 2017. - Vol. 9. - Pp. 688-696. URL: https://link.springer.com/article/10.1134%2FS2070048217060023#citeas (дата обращения: 25.02.2020). DOI: 10.1134/S2070048217060023
- Almgren, A. S. A Conservative Adaptive Projection Method for the Variable Density Incompressible Navier - Stokes Equations / A. S. Almgren, J. B. Bell, P. Colella [et al.]. - // Journal of Computational Physics. - 1998. - Vol. 142, issue 1. - Pp. 1-16. URL: https://www.sciencedirect.com/science/article/pii/S0021999198958909?via%3Dihub (дата обращения: 25.02.2020). DOI: 10.1006/jcph.1998.5890
- Day, M. S. Numerical Simulation of Laminar Reacting Flows with Complex Chemistry / M. S. Day, J. B. Bell. - // Combustion Theory and Modelling. - 2000. -Vol. 4, issue 4. - Pp. 535-556. URL: https://www.tandfonline.com/doi/abs/ (дата обращения: 25.02.2020). DOI: 10.1088/1364-7830/4/4/309
- Metzner, M. Computing Low Mach Number Flows by Parallel Adaptive Multigrid / M. Metzner, G. Wittum. - // Computing and Visualization in Science. - 2006. - Vol. 9, issue 4. - Pp. 259-269. URL: https://link.springer.com/article/10.1007%2Fs00791-006-0025-x#citeas (дата обращения: 25.02.2020).
- DOI: 10.1007/s00791-006-0025-x
- Turkel, E. Assessment of Preconditioning Methods for Multidimensional Aerodynamics / E. Turkel, R. Radespiel, N. Kroll. - // Computers & Fluids. -1997. - Vol. 26, issue 6. - Pp. 613-634. URL: https://www.sciencedirect.com/science/article/abs/pii/ S0045793097000133?via%3Dihub (дата обращения: 25.02.2020).
- DOI: 10.1016/S0045-7930(97)00013-3
- Almgren, A. S. A Numerical Method for the Incompressible Navier - Stokes Equations Based on an Approximate Projection / A. S. Almgren, J. B. Bell, W. G. Szymczak. - 10.1137/ S1064827593244213 // SIAM Journal on Scientific Computing. - 1996. - Vol. 17, issue 2. - Pp. 358-369. URL: https://epubs.siam.org/doi/ (дата обращения: 25.02.2020).
- DOI: 10.1137/S1064827593244213
- Bell, J. B. A Second-Order Projection Method for the Incompressible Navier - Stokes Equations / J. B. Bell, P. Colella, H. M. Glaz. - // Journal of Computational Physics. - 1989. - Vol. 85, issue 2. - Pp. 257-283. URL: https://www.sciencedirect.com/science/article/pii/0021999189901514?via%3Dihub (дата обращения: 25.02.2020).
- DOI: 10.1016/0021-9991(89)90151-4
- Борисов, В. Е. Применение адаптивных иерархических сеток для расчета течений реагирующих газов / В. Е. Борисов, С. Е. Якуш // Физико-химическая кинетика в газовой динамике. -2015. - Т. 16, вып. 2. - 13 с. URL: http://chemphys.edu.ru/issues/2015-16-2/articles/544/(дата обращения: 25.02.2020). - Рез. англ.
- Gear, W. C. Numerical Initial Value Problems in Ordinary Differential Equations / W. C. Gear. -New Jersey: Prentice Hall, 1971. - 253 p.
- Rosenbrock, H H Some General Implicit Processes for the Numerical Solution of Differential Equations / H. H. Rosenbrock. - // The Computer Journal. - 1963. - Vol. 5, issue 4. -Pp. 329-330. URL: https://academic.oup.com/comjnl/article/5/4/329/316388 (дата обращения: 25.02.2020).
- DOI: 10.1093/comjnl/5.4.329
- Goldin, V. Ya. Finding the Solutions of Constant Sign of Ordinary Differential Equations / V. Ya. Goldin, N. N. Kalitkin. - // USSR Computational Mathematics and Mathematical Physics. - 1966. - Vol. 6, issue 1. - Pp. 228-230. URL: https://www.sciencedirect.com/science/article/abs/pii/0041555366900449?via%3Dihub (дата обращения: 25.02.2020).
- DOI: 10.1016/0041-5553(66)90044-9
- Belov, A. A. Modeling of Chemical Kinetics in Gases / A. A. Belov, N. N. Kalitkin, L. V. Kuzmina. - // Mathematical Models and Computer Simulations. - 2017. -Vol. 9. - Pp. 24-39. URL: https://link.springer.com/article/10.1134%2FS2070048217010057 (дата обращения: 25.02.2020).
- DOI: 10.1134/S2070048217010057
- Горобец, А. В. Производительность отечественного процессора Эльбрус-8С в суперкомпьютерном моделировании задач вьгчислительной газовой динамики / А. В. Горобец, М. И. Нейманзаде, С. К. Окунев [и др.]. - // Математическое моделирование. -2019. - Т. 31, № 4. - C. 17-32. URL: https://www.elibrary.ru/item.asp?id=37242382 (дата обращения: 25.02.2020). - Рез. англ.
- DOI: 10.1134/S0234087919040026
- Lyupa, A. A. Simulation of Oil Recovery Processes with the Employment of High-Performance Computing Systems / A. A. Lyupa, D. N. Morozov, M. A. Trapeznikova [et al.]. - 10.1134/ S2070048216020095 // Mathematical Models and Computer Simulations. - 2016. - Vol. 8. - Pp. 129-134. URL: https://link.springer.com/article/10.1134%2FS2070048216020095#citeas (дата обращения: 25.02.2020).
- DOI: 10.1134/S2070048216020095
- Rusanov, V. V. The Calculation of the Interaction of Non-Stationary Shock Waves and Obstacles / V. V. Rusanov. - // USSR Computational Mathematics and Mathematical Physics. - 1962. - Vol. 1, issue 2. - Pp. 304-320. URL: https://www.sciencedirect.com/science/article/abs/pii/0041555362900629?via%3Dihub (дата обращения: 25.02.2020).
- DOI: 10.1016/0041-5553(62)90062-9
- Lax, P. D. Weak Solutions of Nonlinear Hyperbolic Equations and Their Numerical Computation / P. D. Lax. - // Communications on Pure and Applied Mathematics. - 1954. - Vol. 7, issue 1. - Pp. 159-193. URL: https://onlinelibrary.wiley.com/doi/abs/ (дата обращения: 25.02.2020).
- DOI: 10.1002/Cpa.3160070112
- Стадниченко, О. А. Математическое моделирование потоков многокомпонентного газа с энергоемкими химическими процессами на примере пиролиза этана / О. А. Стадниченко, В. Н. Сньтников, В. Н. Сньтников // Вьчислительнье методь и программирование: новье вьчислительнье технологии. - 2014. - Т. 15. - С. 658-668. - Рез. англ.
- Snytnikov, V. N. Autocatalytic Gas-Phase Dehydrogenation of Ethane / V. N. Snytnikov, T. I. Mishchenko, V. N. Snytnikov. - // Research on Chemical Intermediates. -2012. - Vol. 38, issue 3. - Pp. 1133-1147. URL: https://link.springer.com/article/10.1007%2Fs11164-011-0449-x (дата обращения: 25.02.2020).
- DOI: 10.1007/s11164-011-0449-x
- Stadnichenko, O. A. Mathematical Modeling of Ethane Pyrolysis in a Flow Reactor with Allowance for Laser Radiation Effects / O. A. Stadnichenko, V. N. Snytnikov, V. N. Snytnikov. - // Chemical Engineering Research and Design. - 2016. - Vol. 109. -Pp. 405-413. URL: https://www.sciencedirect.com/science/article/abs/pii/S026387621600071X?via%3D йинХдата обращения: 25.02.2020).
- DOI: 10.1016/j.cherd.2016.02.008
- Masyuk, N. Effect of Infrared Laser Radiation on Gas-Phase Pyrolysis of Ethane / N. Masyuk, A. Sherin, V. N. Snytnikov [et al.]. - // Journal of Analytical and Applied Pyrolysis. - 2018. - Vol. 134. - Pp. 122-129. URL: https://www.sciencedirect.com/science/article/pii/S0165237017305594?via%3Dihub (дата обращения: 25.02.2020).
- DOI: 10.1016/j.jaap.2018.05.017
- Жалнин, Р. В. Моделирование течения многокомпонентного реагирующего газа с использованием алгоритмов высокого порядка точности / Р. В. Жалнин, Е. Е. Пескова, О. А. Стадниченко [и др.]. - // Вестник Удмуртского университета. Математика. Механика. Компьютерные науки. - 2017. - Т. 27, № 4. - С. 608-617. URL: http://www.mathnet.ru/php/archive.pht ml?wshow=paper&jrnid=vuu&paperid=612&option_lang=eng (дата обращения: 25.02.2020
- DOI: 10.20537/vm170410
- Жалнин, Р. В. Моделирование течения многокомпонентного химически активного газа на примере пиролиза углеводородов / Р. В. Жалнин, Е. Е. Пескова, О. А. Стадниченко [и др.]. - // Препринты ИПМ им. М. В. Келдыша. - 2017. - №2 101. - 16 с. URL: http://library.keldysh.ru/preprint.asp?id=2017-101 (дата обращения: 25.02.2020).
- DOI: 10.20948/prepr-2017-101
- Shu, C.-W. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws / C.-W. Shu. - // Advanced Numerical Approximation of Nonlinear Hyperbolic Equations. - 1997. - Vol. 1697. - Pp. 325-432. URL: https://link.springer.com/chapter/#citeas (дата обращения: 25.02.2020).
- DOI: 10.1007/BFb0096355


