Моделирование движения жидкости

В наше время несомненным препятствием для физических опытов, особенно в области гидродинамики, является невозможность проведения реальных экспериментов с существующими объектами. Очевидным и неоспоримым преимуществом вычислительной гидродинамики является возможность прогнозирования катастрофических и разнообразных природных явлений (например, паводков). Благодаря существующим в этой сфере методам стало достижимым решение сложнейших задач при сохранении точности и скорости разнообразных вычислений.

Метод SPH фокусируется на дискретных сущностях, называемых частицами [1], и их взаимодействиях. Частицы представляют собой материальные точки с определенными свойствами (плотностью, давлением, скоростью и т. д.), которые перемещаются вместе с потоком жидкости. Гидродинамические свойства оцениваются в позициях частиц и рассчитываются из взвешенного среднего значений на других локальных частицах. Таким образом, каждая частица “сглаживается” по конечному объему постоянной массы [2], и таким образом метод SPH естественно адаптируется к плотности.

Для моделирования движения жидкости методом SPH используются следующие уравнения:

Уравнение импульса:

dV_a    V    PPa  Pb      \

—— = ^- ) ^mb⁽-^ + ~+ ⁿab I ^ a ^ ab^a ) + 9,

dt              \pa   Pb       / где va — скорость, pa — давление, pa — плотность частицы a, nab — вязкий терм, Wab(ha) — сглаживающая функция, g — вектор авитации.

Формула для вязкости с учетом g_a b = ^hvab^rab^/r2ab" + 9 2 , где ^rab = ^ra ^{— r}b ^и v_a b = v_a— V b , а r_k и v_k — положение и скорость частицы, c_a b = (c_a + C b )/2,9² = 0.01h², может быть записана как:

(  ^CabPab + Р Pab nab = {       70b

I 0

если V ab • r ab < 0, иначе.

( 2 )

Уравнение непрерывности:

“^ = ^ m b U ab ' ^ a ^ ab (h a ),                       (3)

b где vab = ua — Ub — относительная скорость частиц

P a

= ^m b W ab⁽ ha), b

где p_a — плотность частицы a, m b -масса частицы b, W_a b (h_a) —сглаживающая функция.

Этот вариант уравнения непрерывности не содержит производной по и может быть использован для расчета плотности на каждом шаге по времени.

Уравнение состояния:

^₽ a = ^SO-¹)'                     ⁽⁵⁾

где B — постоянный коэффициент, p₀ — начальная плотность жидкости,

Y — адиабатический показатель.

Трехмерное моделирование распределение частиц проходит в рамках резервуара, частично заполненного водой. Как показано на рисунке 1, ширина, длина и высота резервуара составляет 2.0 м.

Рис. 1. Геометрия моделируемого пространства в виде куба

Плотность воды составляет р =

1000 ^г, численная скорость звука - с5 = 62.6 М, а коэффициенты искусственной вязкости - <т = 1.2, Р = 2.4. Расстояние между частицами устанавливается равным

А% = 0.023 м, а общее количество частиц жидкости - 262133 (см. рис. 2). Шаг по времени составляет 0.00005 с.

Рис. 2. Начальное расположение всех моделируемых частиц

В начальный момент времени все частицы находятся в состоянии покоя, все границы принято считать непроницаемы- ми. Рисунок 3 показывает распределение частиц в течение 1 с после начального положения.

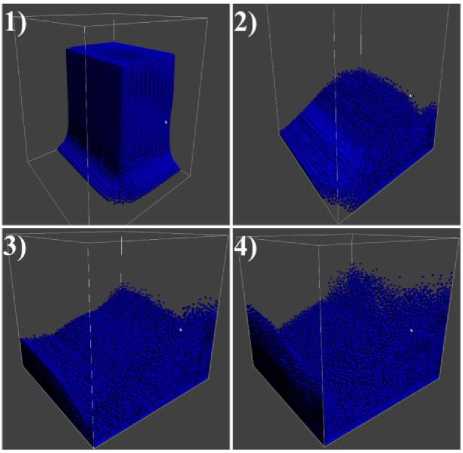
Рис. 3. Расположение моделируемых частиц в процессе вычислений: 1) 0.25 c, 2) 0.5 c, 3) 0.75 c, 4) 1 c.

Можно видеть на рисунке 4, что моделируемая жидкость постепенно угасает и поверхность начинает становится гладкой. В процессе вычислений не возникает каких-либо нереальных явлений, волнения в жидкости постепенно уменьшаются и граничные условия учитываются корректно, не позволяя частицам покидать область моделирования.

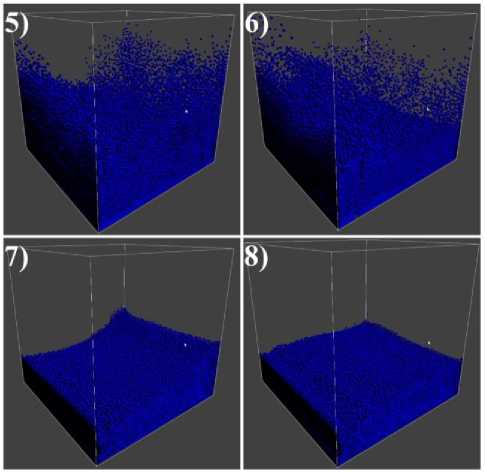
Рис. 4. Расположение моделируемых частиц в процессе вычислений: 5) 1.25 c, 6) 1.5 c, 7)

2.0 c, 8) 2.5 c

Рисунок 5 показывает стоячее положение всех частиц в жидком поле. Можно заметить, что частицы в большинстве своем располагаются на одинаковом расстоя- нии друг от друга. Возмущений не наблюдается, поверхность является ровной, а график распределения давления всех жидких частиц изображен на рисунке 6.

Рис. 5. Конечное состояние системы в процессе выполнения

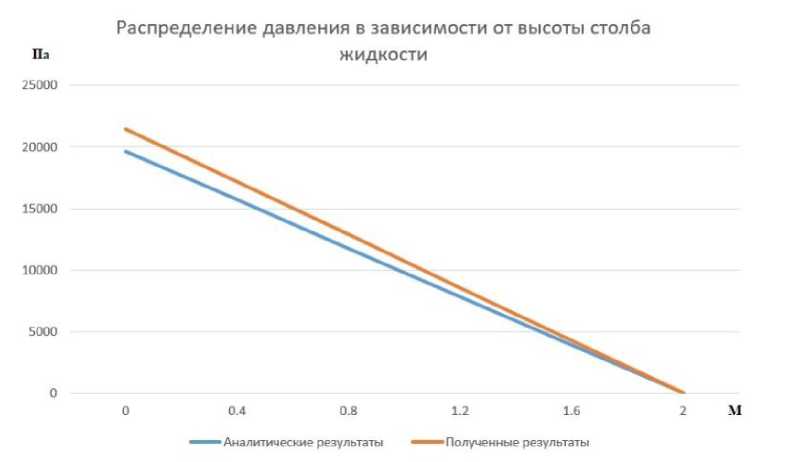
Рис 6. Распределение давления в зависимости от глубины

Анализ и тестирование разработанной программы позволили сделать вывод, что метод SPH является подходящим методом для реализации программного приложения на основе объектно-ориентированного подхода средствами языка С++ и про- граммного интерфейса CUDA, а также что выбор сглаживающего ядра, шага по времени и способа учета граничных условий является ключевым фактором для достижения эффективности и точности вычислений.