Моделирование двугорбых кривых вращения газа в осесимметричном гравитационном поле галактик

DOI:

На сегодняшний день изучение биологических макрообъектов является приоритетным направлением в области биофизики. Исследование физических взаимодействий в биологических объектах позволяет понимать процессы, протекающие внутри живых организмов на молекулярно-атомарном уровне, и формировать фундаментальное представление об их свойствах.

Одним из таких объектов является липидная мембрана. Липидная мембрана выступает неотъемлемой частью клеточных структур, выполняющей барьерную функцию, тем самым регулирующей переход различных веществ внутрь или, наоборот, вовне. Данное свойство мембраны называется проницаемостью, изучение которой способствует развитию таких областей, как фармацевтика, синтетическая биология и биоматериалы [4].

Изучение электрофизических свойств липидных мембран прежде проводилось на практических моделях. Использование таких моделей сильно ограничено из-за сложной архитектуры мембран. В связи с этим большое распространение получило теоретическое исследование липидных мембран методом классической молекулярной динамики, которое активно используют в совокупности с практическими методами.

За последние десятилетия было разработано множество моделей изучения электрофизических свойств липидных мембран методом классической молекулярной динамики. С помощью существующих моделей стали доступны теоретические исследования свойств липидных мембран, невозможные прежде из-за малых пространственных размеров и быстрых временных масштабов многих процессов в биологических системах на молекулярном уровне. Одним из таких процессов, представляющим наибольший интерес с точки зрения прикладного применения, является процесс электропорации — образование гидрофобных пор в липидных мембранах [3; 10; 11].

Разработанные новые модели липидных мембран для использования в исследованиях in silico обладают большой гибкостью и позволяют применять различные типы липидов в бислое, встраивать белковые комплексы в структуру мембраны и погружать образованные липидно-белковые комплексы в растворы, содержащие различные ионы [9]. Такая вариативность позволяет изучать процесс электропорации, учитывая состав и структуру липидной мембраны, а также моделировать важное биологическое явление, связанное с электропорацией, — образование трансмембранных потенциалов [2; 8]. Трансмембранный потенциал (мембранный потенциал) играет важную роль в регуляции жизнедеятельности клетки и выполняет ключевую роль в передаче нервных импульсов между нейронами. С точки зрения моделирования мембранный потенциал достигается путем создания ионного дисбаланса на поверхностях мембраны или воздействием на липидную мембрану электрическим полем [6; 7]. При использовании внешнего электрического поля система начинает действовать как конденсатор. В более ранних работах было проведено моделирование с различными значениями напряженности поля, приложенного к системе со статичной порой в мембране, где вся система проявляет свойства конденсатора [5].

В данном исследовании была использована крупнозернистая (coarse-grained) Martini — модель бислоя липидной мембраны, каждый слой которой состоит из 1 000 липидов типа DPPC(1,2-Dipalmitoylphosphatidylcholine/1,2-дипальмитоилфосфатидилхолин). Представленная мембрана погружена в водный раствор с концентрацией ионов NaCl 1M. На рисунках 1, 2 представлено изображение данной модели.

Рис. 1. Крупнозернистая модель DPPC-мембраны. Частицы, окрашенные в синий (NC ₃ ) и оранжевый (PO ₄ ) цвет, гидрофильные участки липидных структур, формируют верхний и нижний листок мембраны, между ними (в пустом пространстве) заключены гидрофобные участки мембраны. За пределами мембраны расположен водный раствор с ионами Na и Cl фиолетового и зеленого цвета соответственно

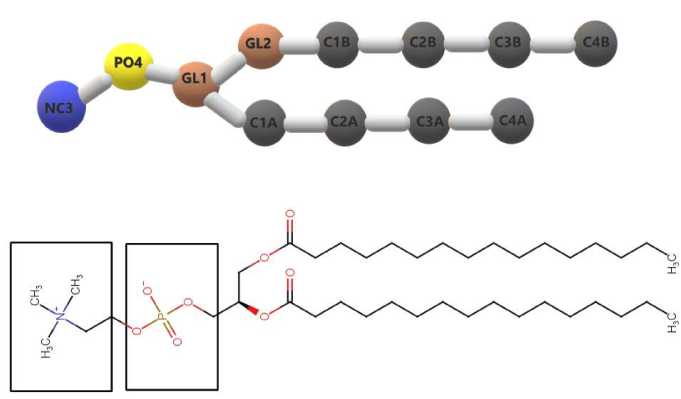
Рис. 2. Полноатомарное представление ( снизу ) и крупнозернистая модель ( сверху ) DPPC-структуры

Моделирование молекулярной динамики было проведено с помощью GROMACS (версия 2021.4) с использованием силового поля martini22p. Предварительно осуществлена минимизация энергии, уравновешивание системы, моделирование без электрического поля и моделирование с приложенным электрическим полем. Минимизация энергии велась с максимальным количеством шагов — 5 000. Уравновешивание системы происходило в 2 этапа: в ансамбле с NVT (постоянное количество частиц, объем и температура); NPT (постоянное количество частиц, давление и температура). Во время первого этапа был использован термостат v-rescale при температуре 298,15 К 0 , на втором этапе — баростат Berendsen.

Во время основного моделирования молекулярной динамики к системе относительно плоскости Z (перпендикулярно мембране) было приложено переменное электрическое поле, действие которого описано по формуле:

(t — t ₀ )²

Е (t) = Е о exp[--⁷ ] cos[ w (t — t o )], 2 0 2

где Е _о — амплитуда напряженности электрического поля, равная 0,073 (В/нм); t ₀ — время достижения пика амплитуды, равной 500 (пс); ω — угловая частота, равная 0,006283 (рад/с); σ — ширина импульса. Так как в данной работе используется переменное электрическое поле и значение о = 0, то исходя из (1) получаем:

Е (t) = Е _о cos[ ^ (t — t ₀ )].

На рисунке 3 представлен график приложенного электрического поля к мембране.

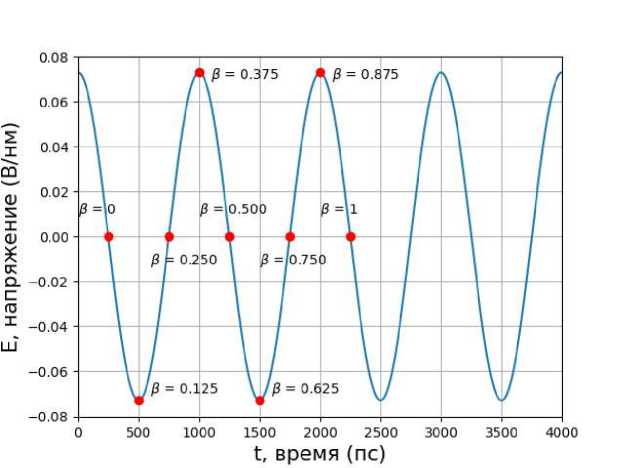
Рис. 3. График действия электрического поля с обозначенными моментами ( красным цветом ) регистрации изменения распределения заряда в системе ( β от 0 до 1)

Анализ результатов основывался на регистрации изменения распределения заряда в системе таких групп частиц, как: PO ₄ , NC ₃ , Na и Cl.

Расчеты осуществлялись с помощью MDAnalysis (библиотека Python для анализа траекторий на основе моделирования молекулярной динамики). При анализе результатов изменения распределения заряда таких групп частиц, как PO4 и NC3, был сделан вывод, что воздействие приложенного электрического поля на данные группы не вызывает значительного изменения распределения заряда. Такое поведение, предположительно, связано с отсутствием возможности NC3 и PO4 свободно перемещаться в системе, так как их движение ограничено положением в структуре мембраны.

В свою очередь, группы Na и Cl, свободно перемещающиеся в системе, но при этом не проходящие через мембрану, в пиковые моменты амплитуды напряжения электрического поля накапливаются на поверхности мембраны, о чем свидетельствуют изменения распределения заряда, представленные на рисунках 4 и 5. В связи с этим сделан вывод, что данная система проявляет свойства, характерные для конденсатора.

Также был проведен анализ зависимости общего заряда ионов Na и Cl от разности потенциала на коробке исследуемой системы. Результаты, представленные на рисунке 6, свойственны для мемконденсаторов (конденсаторы с эффектом памяти) и сопоставимы с результатами в более ранних работах [5].

В работе [5] рассматривается система, схожая с представленной в нашем исследовании, за исключением наличия в мембране постоянной нанопоры, через которую осуществляется переход ионов из одного водного отсека в другой. Авторы работы предлагают возможный механизм проявления свойств, характерных для мемконденсаторов у системы, связывая их появление с возможностью ионов переходить через мембрану. Результаты нашего исследования указывают, что система без нанопор также проявляет свойства, характерные для мемконденсаторов.

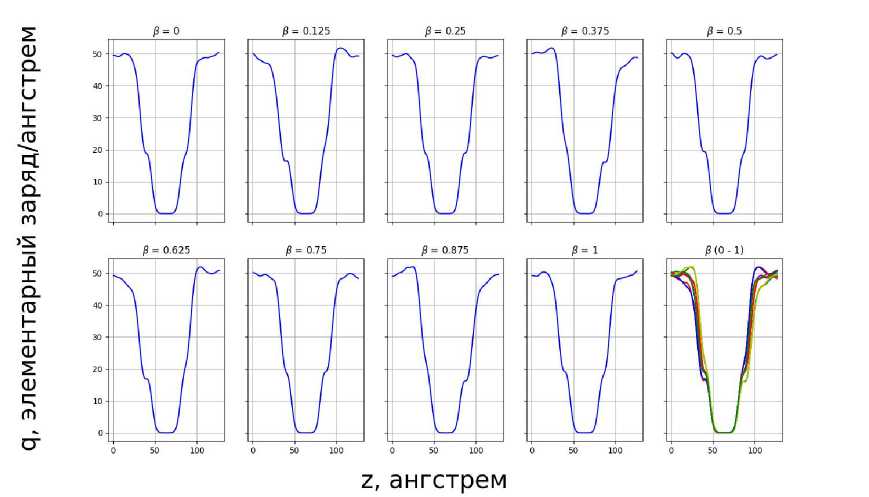
Рис. 4. Распределение заряда Na

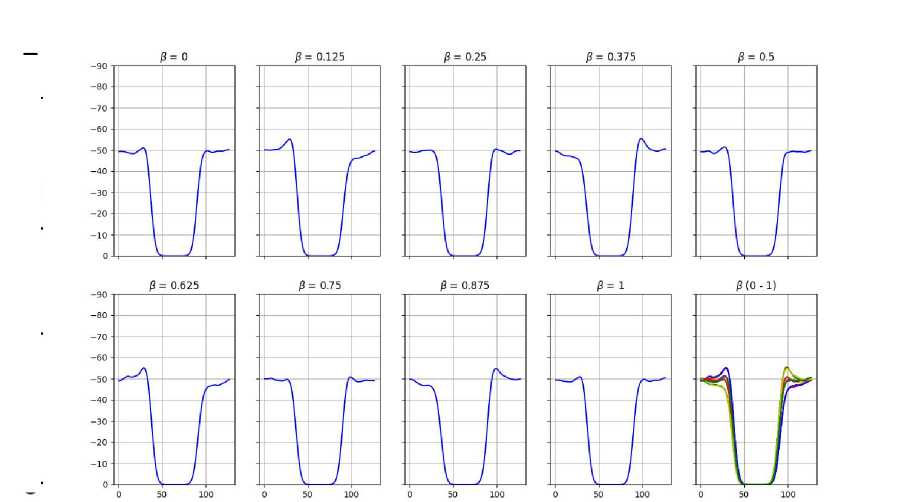
q, элементарный заряд/ангстрем

z, ангстрем

Рис. 5. Распределение заряда CL

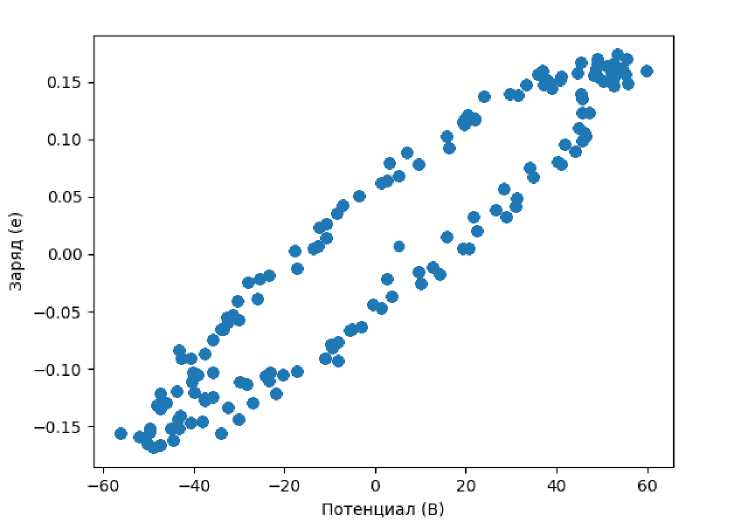
Рис. 6. Петля гистерезиса зависимости потенциала от заряда

Таким образом, на основе полученных результатов сделан вывод, что наша модель действует как система, проявляющая свойства мемконденсатора.

Для расчетов был использован кластер ВолгГТУ [1].