Моделирование двумерного электрического поля одиночного круглого провода над заземленной пластиной с помощью метода конформных отображений

Расчет электрических полей представляет собой практический интерес, но при этом является довольно трудоемким процессом. Как известно, проектирование новых электронных компонентов и систем СВЧ-устройств требует более точных расчетов. Для этого необходимы более точные модели, следовательно, отыскание более эффективных методов моделирования. Одним из таких методов является метод конформных отображений.

Еще в XIX веке Б. Риманом впервые был выдвинут вопрос о конформном отображении, что стало основой для дальнейших исследований в этой области [3].

Основной сложностью метода является нахождение вида самой функции для конкретной реальной системы. На практике при отыскании функции конформного отображения используются либо специальные каталоги конформных отображений, либо она ищется посредством последовательных проб.

Канарейкин Александр Иванович

В частности, моделирование высокочастотных волноведущих связанных линий передачи требует анализа двумерного электростатического поля. Такой анализ, включающий решение задачи Дирихле для решения уравнения Лапласа, осложнен математическими выкладками. Поэтому часто приходится прибегать к специальным компьютерным программам [1; 4–7; 10].

Метод конформных преобразований широко применяется и в других разделах физики [8; 9].

Работа посвящена вопросу расчета сложного двумерного электрического поля круглого провода над заземленной пластиной на основе метода конформных отображений.

Постановка задачи

Пусть дан одиночный круглый провод над заземленной пластиной. Данная конструкция может применяться для передачи СВЧ-энергии. С целью снижения потерь на излучение в пространство между проводом и пластиной помещается плоский слой материала, который представляет собой изолятор с высокой диэлектрической проницаемостью е, как это показано на Рисунке 1.

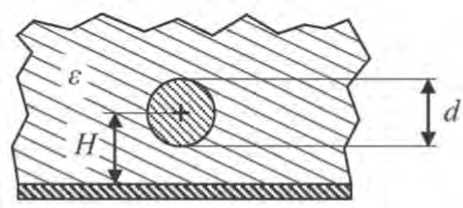
Рисунок 1. Поперечное сечение линии

Решение задачи

Для дальнейших исследований и упрощения расчетов введем декартову систему координат, а саму задачу представим в следующем графическом виде (см. Рисунок 2).

Обозначим Г = z : z - Н | = a - окружность, U - напряженность поля в точке ( x , у ). Известно, что U должна быть гармонической функцией [2], то есть для нее выполняется условие

д2 U + д2U дx 2 ду 2

Моделирование двумерного электрического поля одиночного круглого провода ...

также она должна удовлетворять следующим граничным условиям:

U ( x , y )l x = 0 = ⁰ ; U ( x , y )l г = E о .

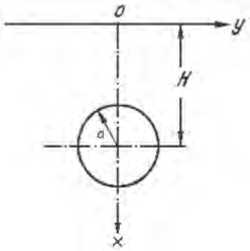
Рисунок 2. Чертеж исследуемой линии

Данная область является двусвязной, поэтому отобразим ее конформно на круговое

КОЛЬЦО: К = { ® : r < H | <  1 } .

В круговом кольце функция U является гармонической в кольце К, и она должна удов- летворять следующим условиям:

1 | Н = r = ^E 0

U |, , = 0 ; U l.

'I Н =i 1|

Задача сводится к решению задачи Дирихле, которая в кольце К имеет вид

U = E 0 log , Н .

Далее проведем проверку, что функция U является гармонической. Для этого рассмотрим вспомогательную функцию

U = ln| z | = ln^ x ² + y ² = —ln( x ² + y 2 ) .

Найдем для нее частные производные второго порядка: d й    x

d x

д1 й

дx2 "

dy д2 U

= 2 x	2 ; + y
2	2
= y	- x
2 ( x	2 2 ; + y )
г	y
= 2	2;
x	+ y
22
x	y

;

^d y 2 ( x ² + y ² )^:

Сложив выражения (7) и (9), получим равенство (1). Таким образом, получили верное

равенство, следовательно, доказали гармоничность исследуемой функции.

Теперь определим параметр r в выражении (4). Для этого рассмотрим произвольную точку, расположенную на расстоянии x = h + a . При отображении ее образом будет точка, лежащая на окружности радиуса H I = r ^:

H + a - V H ² - a¹ r =----------<          .

H + a +7 H ² - a ^г

В результате такого отображения получили дробно-линейную функцию. Как следует из теории, она обладает круговым свойством, а именно: прямые и окружности отображаются сами в себя. Поэтому при помощи данного преобразования отобразим рассматриваемую область на круговое кольцо:

z - c to =-----, z + c

где c = 4 H ² - a ² .

Подставим выражение (6) в (4), получим

U ( x , y ) = E 0 log r

z - V h ² - a ²

z + V H ² - a ²

Тогда искомое решение нашей основной задачи принимает следующий вид:

E=

Eо   J(x2 -c2 + У2)2 + 4c2Уy ln H + c         (x - c)2 + yy

a

Далее воспользуемся выражением для определения поля равномерно заряженного бесконечного цилиндра с линейной плотностью заряда λ:

E 0 =

X

2 ns ₀ s R

В итоге напряженность электрического поля

2  2  22   22

q 1 in V⁽ x ^{- c +} У ) ^{+ 4 c} У 2 n£ 0 £ la in H + c        ( x - c )² + y ²

a

Как видим, полученное выражение оказалось достаточно простым. Оно содержит в основном дроби и логарифмические выражения, что показывает преимущество метода конформного отображения.

Далее для наглядности полученного результата построим график электрического поля для данного случая с конкретными параметрами. Пусть расстояние H относится к радиусу a в отношении 5/3. Далее подставим данные в формулу (10). Для удобства в построении приведем напряженность поля к безразмерному виду

4 ( x ² + y ² - 16)² + 64 y ² ( x - 4)² + y²

9 = in

На Рисунке 3 представлен трехмерный график поля для данного случая.

Как видно из рисунка, полученное решение (10) удовлетворяет заданным граничным условиям (2).

Заключение

Таким образом, раскрыты понятие и сущность самого метода конформных отображений. Получена формула для нахождения электрического поля одиночного круглого провода над заземленной пластиной. С ее помощью можно анализировать приведенную конструкцию с целью уменьшения потерь при передаче СВЧ-энергии. Показано преиму-

Моделирование двумерного электрического поля одиночного круглого провода ...

щество применения данного метода при нахождении электрического поля круглого провода над заземленной пластиной, что может быть полезным для практических расчетов электрических полей сложных систем.

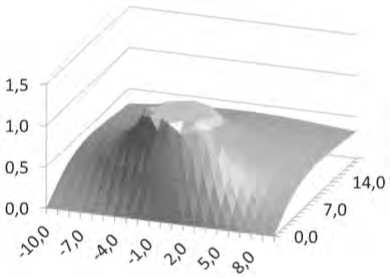
Рисунок 3. Электрическое поле линии круглого провода над заземленной пластиной при H / a = 5/3