Моделирование ферментативных процессов в двенадцатиперстной кишке для прогнозирования областей повышенного риска функциональных нарушений

К основным функциям ДПК относятся эвакуа-торная, моторная, секреторная и всасывательная. Задача моторной функции заключается в перемешивании химуса с пищеварительными ферментами. Эва-куаторная функция отвечает за перемещение химуса в последующие отделы кишечника. Секреторная функция заключается в выделении кишечного сока. Кроме того, в ДПК происходит активное всасывание содержимого тракта, в том числе элементарных компонент пищи (аминокислот, глицеридов, моносахаридов), воды, минеральных солей, витаминов. Однако, по сравнению с последующими отделами тракта, интенсивность всасывания, особенно компонент пищи, в ДПК существенно меньше4.

К методам исследования пищеварительных процессов относятся экспериментальные методы. С помощью них можно получить данные о форме и размере органа, изучить состав пищеварительных соков, определить уровень кислотности, обнаружить заболевания пищеварительной системы и т.д. Недостатками существующих методов являются дороговизна оборудования, необходимость привлечения высококвалифицированных специалистов, отсутствие возможности количественно спрогнозировать функциональные нарушения.

Методы математического моделирования в медицине помогают проводить огромное количество исследований, численных экспериментов, которые невозможно реализовать в натурных экспериментах из-за низкого уровня развития экспериментальной техники или вероятной опасности для здоровья человеческого организма. Реальные физиологические эксперименты могут быть заменены на вычислительные. Преимущество таких экспериментов в том, что можно изучать влияние как отдельных факторов (в том числе при больших нагрузках), так и их сочетаний на организм человека, получать большой объем экспериментальных данных за небольшой промежуток времени, строить на полученных результатах прогнозы развития заболеваний [5].

Математическое моделирование позволяет учитывать условия, в которых протекает пищеварение, геометрию органов, их функциональные нарушения, анализировать воздействие отдельных факторов на органы пищеварения. В настоящее время развиваются подходы к численному моделированию процесса течения в различных участках ЖКТ, преимущественно модели в двумерной постановке, трехмерные модели стали использоваться в основном в последнее десятилетие [6–8]. В ранее опубликованных работах исследователи больше внимания уделяли моторике тракта, а не пищеварительным процессам [9–14]. В статье B. Hari et al. [15] ДПК моделировалась как двумерный канал с подвижными границами и с выделением граничного слоя для описания проницаемых стенок тракта. Химус был рассмотрен как многокомпонентная, двухфазная смесь, при этом рассматривалась только одна реакция гидролиза крахмала под воздействием амилазы. С одной стороны, развитие подобных моделей может привести к открытию новых, ранее неизвестных механизмов формирования заболеваний пищеварительной системы. С другой стороны, данный подход имеет большие перспективы в практическом использовании, включая выработку рекомендаций по лечению, а также по особенностям питания для конкретного пациента. В связи с этим в предложенной авторами модели предполагается усовершенствовать существующие подходы, учесть секрецию и всасывание веществ, их химическую и физическую обработку под воздействием пищеварительных соков и моторики желудочно-кишечного тракта, а также нарушения пищеварительных процессов.

Цель исследования – разработка математической модели одного из отделов желудочно-кишечного тракта – двенадцатиперстной кишки для прогнозирования областей повышенного риска функциональных нарушений.

Материалы и методы. Будем рассматривать двенадцатиперстную кишку, для которой характерно распространение перистальтических волн по направлению к тонкому кишечнику со значительной степенью сжатия мышц стенки (амплитудой) [16].

Моторика ДПК является периодичной, и параметры перистальтических волн не зависят от состава пищи.

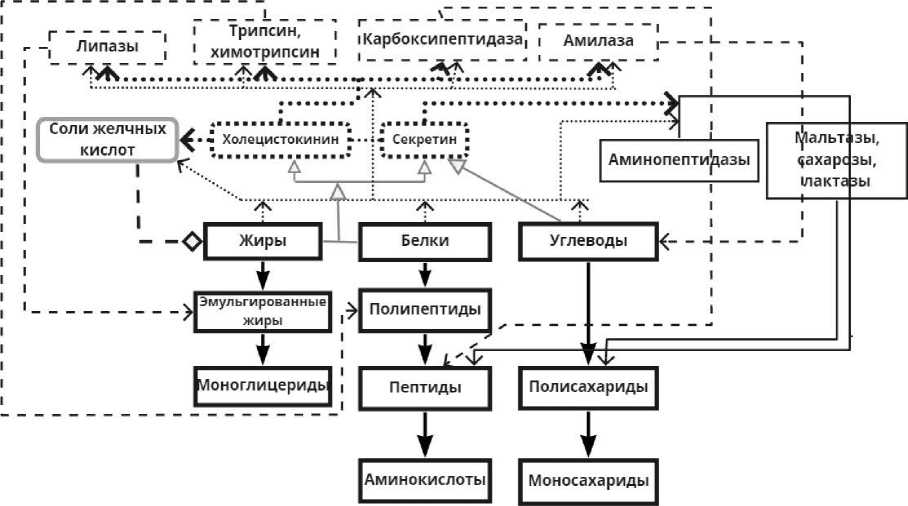
Создаваемая математическая модель ДПК должна описывать свойства жидкости, поэтому необходимо подробно рассмотреть химические реакции, протекающие в этом отделе кишечника, в результате которых происходят изменения в составе химуса. На рис. 1 представлена упрощенная схема преобразования пищи под воздействием пищеварительных соков и регуляция их секреции нервным и гуморальным путем.

По представленной упрощенной схеме под воздействием поступающих жиров, белков и углеводов эндокринные и экзокринные клетки начинают выделять гормон холецистокинин и секретин, которые стимулируют секрецию компонент желчи, ферментов кишечного и панкреатического сока. Нервная регуляция происходит за счет раздражения блуждающих и чревных нервов, увеличивающих и уменьшающих секрецию пищеварительных соков. Таким образом, благодаря нервным и гуморальным механизмам регуляции в ДПК начинается секреция необходимых компонент и ферментов для распада веществ на более простые соединения. Соли желчных кислот и липаза расщепляют жиры до моноглицеридов. Под воздействием трипсина, химотрипсина,

Регуляция гормонами

Компоненты пищи

Гормоны

Фермент кишечного сока

Фермент панкреатического сока

Влияние ферментов панкреатического сока

Компонента желчи

Нервный сигнал

Раздражение слизистой оболочки

Влияние ферментов кишечного сока

Рис. 1. Схема преобразования компонент пищи в ДПК

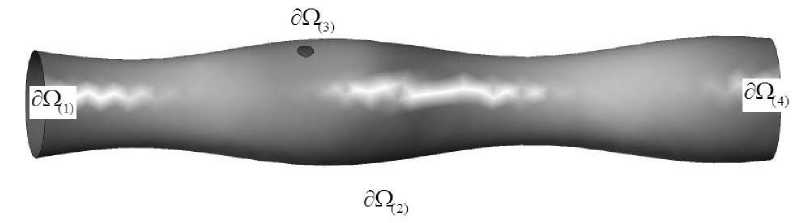
Рис. 2. Выделение подобластей по функциональному признаку

карбоксипептидазы, аминопептидазы происходит гидролиз полипептидов до аминокислот, под воздействием амилазы, мальтазы, сахарозы осуществляется гидролиз сложных углеводов до моносахаридов. В отличие от ферментов поджелудочной железы ферменты ДПК действуют на продукты промежуточного гидролиза питательных веществ.

Таким образом, химус будет рассматриваться как многокомпонентная вязкая жидкость, состоящая из (индекс i =0,I): углеводов (крахмал) ( i = 0), панкреатической амилазы ( i = 1), воды ( i = 2), глюкозы ( i = 3), белков ( i = 4), полипептидов ( i = 5), пептидов ( i = 6), аминокислот ( i = 7), жиров ( i = 8), эмульгированных жиров ( i = 9), моноглицеридов ( i = 10), липаз ( i = 11), трипсина ( i = 12), карбоксипептидазы ( i = 13), солей желчных кислот ( i = 14), аминопептидаз ( i = 15), мальтазы, сахарозы, лактазы ( i = 16). Гормоны (холецистокинин и секретин) не являются компонентами смеси и воздействуют через кровеносную систему, их влияние на характеристики процесса пищеварения планируется рассмотреть в дальнейших исследованиях.

ДПК разбивается на L областей, где ∂Ω ₍₁₎ – сечение входа, ∂Ω ₍₂₎ – область секреции кишечного сока и всасывания компонент, ∂Ω ₍₃₎ – область секреции желчи и панкреатического сока (фатеров сосочек), ∂Ω ₍₄₎ – сечение выхода жидкости из ДПК (рис. 2).

Секреция пищеварительных соков и всасывание компонент химуса описаны с помощью массовых источников / стоков в трубе в пристеночном слое. Функциональные нарушения секреции влияют на интенсивность массовых источников.

Уравнения сохранения массы для компонент смеси с учетом массовых источников за счет секреции и ферментативной реакции записаны в виде:

_∂ ^∂ _t (ρ Y ( i ) ) + ∇ ⋅ (ρ v Y ( i ) ) =- ∇ ⋅ J ( i ) + R ( i ) + S ( i ) , r ∈Ω , t ∈ [0; T ), i =0, I ,           (1)

где r – радиус-вектор пространственных точек, м;

ρ – плотность среды, кг/м3;

Ω – внутренность всей области;

∂Ω – граница области;

Ω=Ω ∪ ∂Ω – замкнутая область (внутренность области и ее граница);

∂Ω _{( l )} – l -я граница области, l =1, L ;

Ω _{( l )} – внутренность области, прилегающая к l -й границе, l =1, L ;

v – скорость частиц среды, м/с;

Y _{( i )} – массовая доля i -й компоненты;

J _(i) – вектор интенсивности потока массы i -й компоненты за счет диффузионных процессов, кг/(м²∙с), i =0, I ;

R _{( i )} – интенсивность источника массы i -й компоненты за счет реакций между компонентами, кг/(м³∙с), i =0, I ;

S _{( i )} – интенсивность массового источника i -й ком по ненты в области за счет секреции, кг/(м³∙с), i =0, I .

В гомогенной смеси каждая компонента занимает весь ее объем, массовая доля (или процентная концентрация вещества) – это отношение массы растворенного вещества к общей массе раствора, ее отличие от концентрации в том, что эта величина является безразмерной и выполняется условие:

∑ _i Y ( i ) = 1, i = 0, I .                (2)

Уравнение сохранения импульса для вязкой многокомпонентной жидкости имеет вид:

∂

(ρ v ) + ∇ ⋅ (ρ vv ) =- ∇ p + ∇ ⋅ τ + ρ g ,

∂t r∈Ω, t∈[0;T),               (3)

где p – давление (Па); τ – девиаторная часть тензора напряжений Коши (Па), которую для вязкой несжимаемой жидкости можно записать в виде:

τ =η ( ∇ v + ( ∇ v ) ^T ), r ∈ Ω ,         (4)

где η – сдвиговая вязкость, Па∙с.

Вектор интенсивности потока массы i -й компоненты за счет диффузионных процессов может быть представлен в виде:

J (i) = - ρ K ( i ) ∇ Y ( i ) ,                   (5)

где K(i) – коэффициент диффузии i-й компоненты в полости ЖКТ, м2/с, i =0,I . В первом приближе- нии K(i) предполагается одинаковым для всех компонент.

Молярную концентрацию M _{( i )} i -й компоненты можно представить в виде:

C (i) = ! ( , ) р/ M ( i ) .                    (6)

Скорость секреции фермента в области l определяется соотношением:

^S ( i )( l )

⁵ ( i )( i )

^s ( i )( l )^{[ρ Y} ( i )^]( l )

⁵ '( i )( i ) + ^[p Y i ) ] ( i )

где s(0i)(l) – базовый уровень секреции фермента (в от- сутствие пищи) в области Ql), кг/(мЭ-с);

s _{( i )( l )} – константа скорости секреции фермента в области Ц l ) , равная максимальной скорости секреции, кг/(м³∙с);

s ' _{( i )( l )} – вторая константа скорости секреции в области Ц l ) , равная средней массовой концентрации компонент, усиливающих секрецию данного фермента, в момент, когда скорость секреции принимает значение равное половине максимальной скорости, кг/м³;

[ р У^i ) ] ( l ) - средняя массовая концентрация компонент, от которых зависит секреция фермента, вблизи стенки тракта, кг/м³.

Источник массы за счет ферментативной реакции имеет вид:

^k ( j )( k )^{ρ2 Y} ( j ) ^Y ( k )^{/ M} ( k )

R а) = -----——— k (j)(к)+ р Yj) /M(j)

где k , k ^'   – константы скорости ферментатив-

( j )( k )       ( j )( k )

ной реакции, 1/с, кмоль/м³, R _{( i )} принимает отрицательное значение для реагента и положительное – для продукта реакции;

Y _{( j )} , Y _{( k )} – массовые доли вещества и фермента;

M _{( k )} , M _{( j )} – молярные массы.

Данная формула является соотношением Михаэлиса – Ментен для описания скорости ферментативной реакции. Пределом скорости реакции является константа k , вторая константа скорости k ^' ( j )( k )                                                                         ( j )( k )

равна концентрации вещества, вступающего в реакцию, в момент, когда скорость реакции принимает значение равное половине предельной скорости.

Скорость всасывания компонент смеси определяется:

^ ( i )( i ) = ^{- 5}(t)(i ) (^{[p Y}(ii ) ^] ( i ) ^- h ( i ) ^C ( i )) ,            ⁽⁹⁾

где s _{( i )( l )} > 0 – константа скорости всасывания i- й компоненты в области Q _i ) , 1/с;

[ρ Y _{( i )} ] _{( l )} – средняя массовая концентрация вблизи стенки l , кг/м³;

C ₍ ^b _{i )} – массовая концентрация i- го химического вещества в крови, кг/м³;

h ( i ) - коэффициент пропорциональности, показывающий при каком соотношении концентраций начинается диффузия.

В разрабатываемой модели на данном этапе предполагается, что отсутствует прилипание на стенках:

v ( t , r ) = ddtt ), t e [0; T ), r ( t ) e 5Ц. i ) , I = 2,3, (10)

где r ( t ) e 9Ц- ₁ ) - радиус-вектор материальной точки стенки ДПК. На границе 5Ц- 1) задаются значения массовых долей компонент смеси Y ( i ) = У® Ц , скорость потока, условия равенства нулю касательных компонент вектора напряжений:

v ( t , r ) = v in , t - ( n - a - n)n = 0 , t = n - ст , t e [0; T ), r едЦ. _i ) , i = 1,4

Система уравнений дополняется начальными условиями в виде:

Y (i) (t , r ) = } ^⁰) , v ( t , r ) = v ⁰, r eQ , t = 0.

Результаты и их обсуждение. В данном исследовании численный эксперимент проведен для реакции гидролиза крахмала под воздействием амилазы. ДПК рассматривается как труба длиной 0,28 м и диаметром 0,04 м, для которой характерно распространение перистальтических волн с заданными характеристиками: период – 20 с, амплитуда – 0,0035 м, скорость - 5 - 10 ^{- 3} м/с [17]. При наличии нарушений моторной функции данные параметры могут варьироваться.

Химус представлен как многокомпонентная вязкая жидкость, состоящая из (индекс i =0, I ): углевода (крахмал) ( i = 0), воды ( i = 2). В процессе продвижения по трубе смесь меняет свой состав под воздействием панкреатической амилазы ( i = 1), в результате образуется глюкоза ( i = 3).

Секреция амилазы будет описана с помощью массового источника в трубе в пристеночном слое на границе 5О (_Э) , находящегося на расстоянии 0,1 м от сечения входа, диаметр отверстия равен 0,006 м. Интенсивность источника со временем не меняется.

Константы скорости реакции задаются равными к(0)(1) = 408 1/с, к(0)(1) = 10-Экмоль/м3 [18]. Молекулярные массы крахмала и амилазы взяты из литературных источников: M(0) = 828,7, M(1) = 54000 г/моль [19]. Интенсивность источника амилазы принимается равной 0,01 кг/(м3∙с), для воды – 0,1 кг/(м3∙с), что соответствует активной фазе кишечного пище- варения. Скорость потока смеси на входе задавалась равной 0,001 м/с, молярная доля крахмала – равной 0,05.

Ранее записанная система уравнений для описания процесса пищеварения в ДПК решалась при помощи вычислительного пакета Ansys. Временной шаг равен Δ t = 0,1 c. В начальный момент времени задана смесь из компонент воды и крахмала. На рис. 3–5 представлено распределение компонент смеси в трубе.

На рис. 3 представлена массовая доля крахмала в разные моменты времени. Из приведенных результатов видно, что с течением времени крахмал распределяется по трубе, и максимальная концентрация вещества не превышает 0,036, то есть не весь крахмал вступает в химическую реакцию. В работе [20] был проведен эксперимент, в результате которого из 5%-ного раствора крахмала под воздействием амилазы было преобразовано не более 25 % крахмала в глюкозу за время 11 000 c. В данной статье численный эксперимент был проведен до 600 с, так как целью являлся анализ распределения концентрации веществ с учетом химической реакции и перемешивания компонент за счет подвижных стенок трубы.

На рис. 4 под воздействием движущихся стенок, благодаря которым происходит перемешивание компонент смеси, и выделяемой из области ∂Ω ₍₃₎ амилазы, ко времени 100 с образуется глюкоза

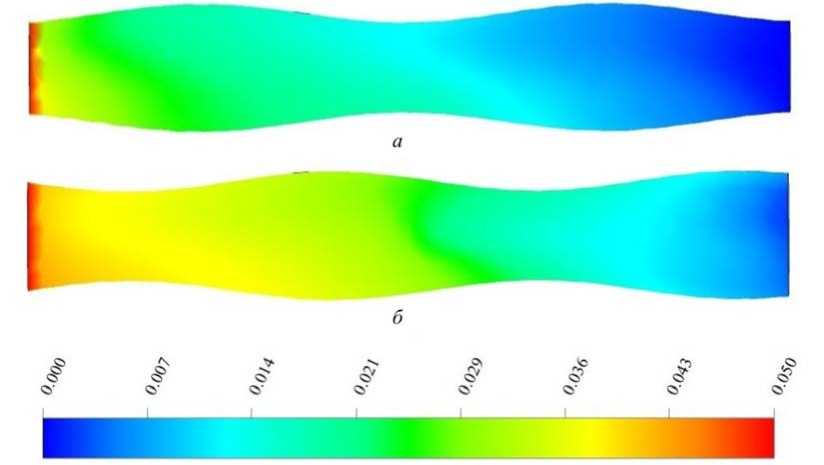
Рис. 3. Массовая доля крахмала в моменты времени: a – 100 с; б – 600 с

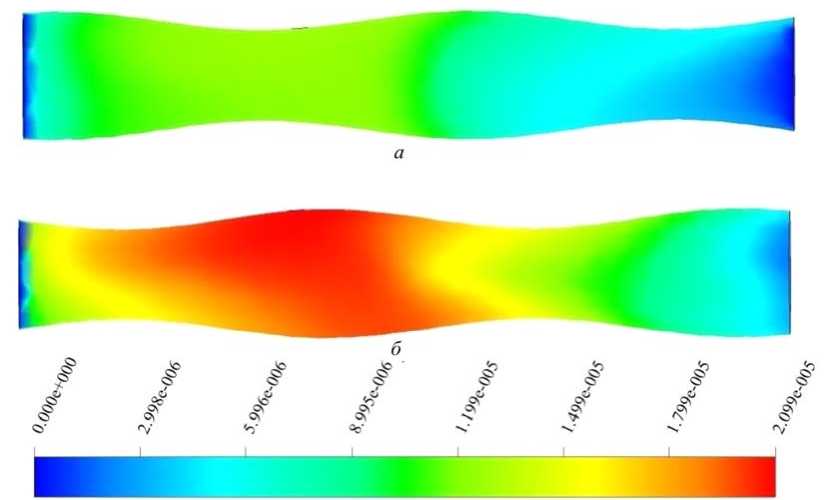
Рис. 4. Массовая доля глюкозы в моменты времени: a – 200 с; б – 600 с

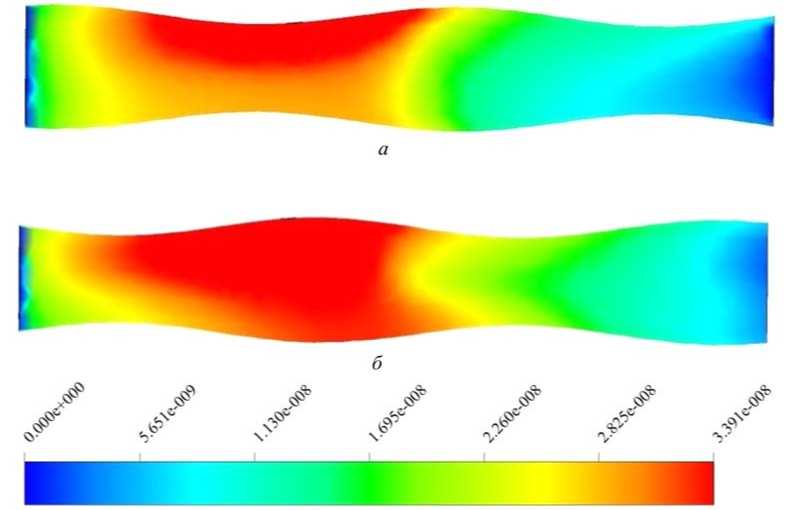
Рис. 5. Массовая доля амилазы в моменты времени: a – 200 с; б – 600 с

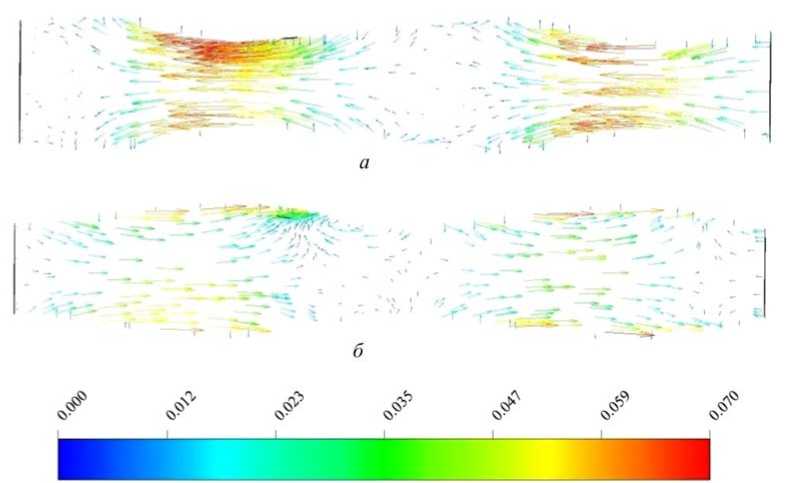
Рис. 6. Поле скорости (м/с) в моменты времени: a – 533 с; б – 550 с

с максимальным полем концентрации, равным 9,5∙10–6, значение которого с течением времени увеличивается и на 600 с достигает значения, равного 2∙10–5. Область большей концентрации продукта реакции расположена у массового источника, ближе к выходу из ДПК концентрация вещества уменьшается. Вероятно, это может быть обусловлено тем, что временные масштабы скорости реакции больше, чем масштабы переноса среды, и, кроме того, происходит обратный заброс воды из-за заданного движения стенок трубы.

На рис. 5 представлено распределение амилазы в трубе, под ее воздействием происходит хими- ческая реакция, результатом которой является глюкоза. Из представленных результатов видно, что в процессе течения амилаза начинает заполнять канал. Максимальное значение концентрации равно 3,3∙10–8. Выделенного количества хватает для образования глюкозы, концентрация которой в рассматриваемой области в момент времени 600 с выше концентрации амилазы.

Исходя из приведенных результатов на рис. 6, можно говорить, что при заданном перистальтическом движении существуют области, в которых направление скорости обратно распространению волны (в местах сжатия трубы). За счет этого эффекта происходит перемешивание компонент смеси и ее обратный заброс со скоростью 0,023 м/с. Максимальная скорость течения находится в области секреции амилазы (пристеночном источнике) в момент сжатия стенки и равна 0,07 м/с. Полученные результаты согласуются с данными, представленными в статье [15], где ДПК моделировалась как двумерный канал с подвижными границами, скорость в области сжатия была наибольшей и равной 0,05 м/с.

Выводы. Представленная работа посвящена разработке математической модели двенадцатиперстной кишки, позволяющей учитывать условия, в которых протекает преобразование веществ, форму и размер органа, характер моторики кишки, наличие функциональных нарушений. В модели учитываются процессы всасывания веществ, изменения состава жидкости в процессе ее перемещения по трубе.

На данный момент разработана концептуальная и математическая постановка, в результатах рассмотрен один из примеров приложения модели, а именно реакция гидролиза крахмала в ДПК с учетом перистальтического движения стенок, которое обеспечивало перемешивание компонент смеси с поступающей амилазой. Представлены результаты концентраций веществ в различные моменты времени, а также поле скорости. В дальнейшей работе планируется учесть все компоненты и химические реакции, представленные на рис. 1.

Актуальной проблемой остается исследование изменения физико-механических характеристик смеси в процессе течения. На следующем этапе разработки модели планируется учесть всасывание и рассмотреть различные сценарии с функциональными нарушениями секреторной / всасывательной функции и моторики кишечника, влияние гормональной регуляции через гормон секретин и холецистокинин.

В первую очередь научный и практический интерес будут представлять результаты по распределению кислотности в различных участках дуоденума. В перспективе разработанная модель может быть использована как неинвазивный диагностический метод в клинической практике, на основе персональных данных можно будет прогнозировать области повышенного риска развития функциональных нарушений, образования язв и других дефектов слизистого покрова тракта. Также результаты численного моделирования помогут выявить, какие именно нарушения влияют на аномальную кислотность в дуоденуме, что в перспективе поможет врачу назначить индивидуальное лечение, персональный режим питания.

Финансирование. Исследование не имело спонсорской поддержки.