Моделирование формы кулачка, обеспечивающей оптимальную работу высевающего устройства вибрационного типа
Автор: Богульский И.О., Богульская Н.А.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Технические науки
Статья в выпуске: 2, 2017 года.
Бесплатный доступ
При высыпании гранул появляются эф-фекты, вызванные дискретностью среды, ее неоднородностью, нелинейным характером взаимодействия гранул, их переупаковкой, возникновением зон разрыхления и уплотне-ния. Ранее были получены результаты приме-нения имитационного моделирования для ис-следования поведения гранулированной среды в вибрирующих сосудах. Подход оказался до-статочно эффективным и позволил в даль-нейшем решить ряд прикладных задач по со-вершенствованию конструкции универсально-го высевающего устройства, основанного на вибрации лотка с семенами. Основным кри-терием эффективности решения сформули-рованных задач является равномерность вы- сева семян через отверстия дна. Оптимиза-ция процесса велась в двух направлениях. Оп-тимизировались геометрические параметры конструкции - ширина лотка, высота запол-нения семенами, расположение высевающих отверстий в дне и т.д. Проводилась оптими-зация механических параметров - амплитуды и частоты колебаний лотка. Единственное, что оставалось неизменным, было то, что лоток совершал гармонические колебания. В работе сделана попытка оптимизировать работу вибрационного высевающего аппарата в зависимости от формы поверхности кулач-ка, т.е. от режима горизонтальных колебаний лотка. Модель движения гранулированной сре-ды в качестве сил взаимодействия предпола-гает упругие силы контактного взаимодей-ствия между соседними частицами, силы тре-ния между соседними гранулами, стенками и дном и вязкие силы, введенные по аналогии с жидкими средами. Эти вязкие силы достаточ-но реальны и характеризуют влажность рас-сматриваемого объема. В модели вязкие силы необходимо вводить для корректного числен-ного решения задачи. Так как задача Коши, возникающая в данном случае, является до-статочно жесткой - собственные числа опе-ратора перехода чисто мнимые. В этом слу-чае даже энергетически согласованная схема Рунге-Кутта второго порядка, используемая в работе, недостаточно обеспечивает числен-ное решение искусственной, вычислительной вязкостью. Поэтому введение физической, релеевской вязкости хорошо стабилизирует численное решение. Разумный компромисс находится только при множественном вычис-лительном эксперименте.
Гранулированная среда, сплайн-интерполяция, численное моделирова-ние
Короткий адрес: https://sciup.org/14084859
IDR: 14084859 | УДК: 631.331.62-6
Текст научной статьи Моделирование формы кулачка, обеспечивающей оптимальную работу высевающего устройства вибрационного типа
Введение. Статья продолжает цикл работ авторов, посвященных исследованию поведения гранулированной среды в вибрирующих сосудах. Вибрация изменяет свойства среды, делает ее более текучей. Процесс высыпания гранул через отверстия в дне сосуда в чем-то схож с вытеканием жидкости. Но при этом есть существенные отличия. При высыпании гранул появляются эффекты, вызванные дискретностью среды, ее неоднородностью, нелинейным характером взаимодействия гранул, их переупаковкой, возникновением зон разрыхления и уплотнения. В работах [1–3] приведены результаты применения имитационного моделирования для исследования поведения гранулированной среды в вибрирующих сосудах.
Подход оказался достаточно эффективным и позволил в дальнейшем решить ряд прикладных задач по совершенствованию конструкции универсального высевающего устройства, основанного на вибрации лотка с семенами. Было предложно решение ряда задач движения гранулированной среды не только в плоских лотках, но и в высевающих устройствах роторного типа, а также для гранул неправильной формы [2].
Основным критерием эффективности решения сформулированных задач является равномерность высева семян через отверстия дна. Оптимизация процесса велась в двух направлениях. Оптимизировались геометрические параметры конструкции – ширина лотка, высота заполнения семенами, расположение высевающих отверстий в дне и т.д. Проводилась оптимизация механических параметров – амплитуды и частоты колебаний лотка.
Единственное, что оставалось неизменным, было то, что лоток совершал гармонические колебания. Однако технологически выполнить кулачок с поверхностью заданной формы не составляет принципиальной сложности. В данной работе приведены результаты оптимизации работы вибрационного высевающего аппарата в зависимости от формы поверхности кулачка, т.е. от режима горизонтальных колебаний лотка.
Задавать форму кулачка можно множеством различных способов. В работе выбрана аппроксимация кубическими сплайнами [4], причем в простейшем варианте, когда один период функции формы разбивается на два интервала: монотонно возрастающий и монотонно убывающий.
К выбору интерполяции кубическими сплайнами привел как достаточно простой и устойчивый аналитический расчет поверхности кулачка, так и то, что именно сплайновое представление кривых и поверхностей используется при управлении работой металлорежущего инструмента на станках с числовым программным управлением. Кроме того, это обеспечивает достаточно гладкую аппроксимацию.
В качестве желаемой формы поверхности кулачка можно выбрать практически любую, задав разбиение периода на внутренние интервалы. В данной работе выбрано два участка – возрастающий и ниспадающий.
Цель работы . Определение зависимости поведения гранулированной среды в вибрирующем лотке от формы поверхности кулачка. Так как различные формы поверхности обеспечивают различные режимы движения лотка – от равномерного до существенного неравномерного – сдергивания.
Методика расчета. В полярных координатах p , (p уравнение поверхности кулачка можно записать
Р = Ро + (((Р)> где величина р0 постоянна, а изменение дополнительного радиуса х(<р) будем строить в виде двух ветвей/L( ср )и f2(p ), представляющих кубическую сплайн-интерполяцию функции %(<р) на отрезках [0, а] и [ а, 2тт] (рис. 1).
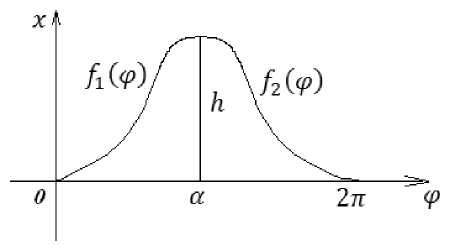
Рис. 1. Форма поверхности кулачка
Функции Ди /2 будем искать в виде: Учитываем краевые условия:
f i = fli + ap<Р + ap Р 2 + a4p3 (1) f i (0) = 0 => a i=0;
[(0) = 0 => a2=0;
fi = bL + Ь(Р(p - 2л) + b 3( p - 2tt)2 + f2(27г) = 0 => b^oQ;
+^(Р — 2л)3. (2) f2 (2л) = 0 => bo-0-
С учетом краевых условий получаем:
A= + a4(p3; fi. = (Ф-271 )2+ bi (
При V= функции fl. и fz совпадают и при- нимают значение h. Также совпадают первые и вторые производные этих функций. Оконча- тельно коэффициенты a3 , b3 , a 4. , bi выража- ются через aи h по формулам (7):
_ 3hn
^3 =- “ ;
6 a2 ( a-2n )
, 37m
D? = ;
3 a ( a-2n );
h ( a+n )
a ( a-2n )․
Вычислительный эксперимент проведем задав шаг Δ(p = ․ Значение текущего шага в ходе расчетов (p=n∙∆Ф. Выполняем оптимиза- цию формы кулачка в зависимости от значений a= ∙∆(p и h, где a – точка сопряжения.
При n < Ni : x= а3ф2 + a4(p3 , n ≥ :
x=Ьз
(
-2
n
)2+
bi
(
Ф
-2
77
)3
.
В качестве критерия равномерности высева в программе вычисляется дисперсия случайной величины, принимающей значения разности количества выпадений через различные отверстия в дне лотка. Результаты исследования. Вычисления выполнялись для прямоугольного лотка шириной 50 см (рис. 2). Первоначально он заполнен гранулами на высоту 30 см. Бункер заполнен гранулами и обеспечивает пополнение лотка в процессе работы. Гранулы представляют собой шарики диаметром 0,8 см. В дне лотка расположены 3 отверстия диаметром 2,5 см. Плотность гранул принята равной единице. Жесткость упругого взаимодействия задана такой, чтобы в неподвижном положении на плоскости деформация гранулы под действием веса составляла 1/10 радиуса. Круговая частота периодического движения принята равной 10 гц. Это соответствует тому, что вращение напрямую передается с вала отбора мощности. Изменение частоты с помощью редуктора не предусматривалось. Релеевская вязкость принята равной 7–14 кг/с. Рис. 2. Результаты эксперимента для симметричной поверхности кулачка
Эксперимент показал, что для среды с небольшой вязкостью наименьшая дисперсия, а значит большая равномерность высева, достигается для точки сопряжения в середине интервала [0,
2
77
]. Увеличение вязкости приводит к существенному изменению в поведении среды.
Выпадение через отверстия становится неравномерным, образуются зоны застоя, что согласуется с возрастанием величины дисперсии.
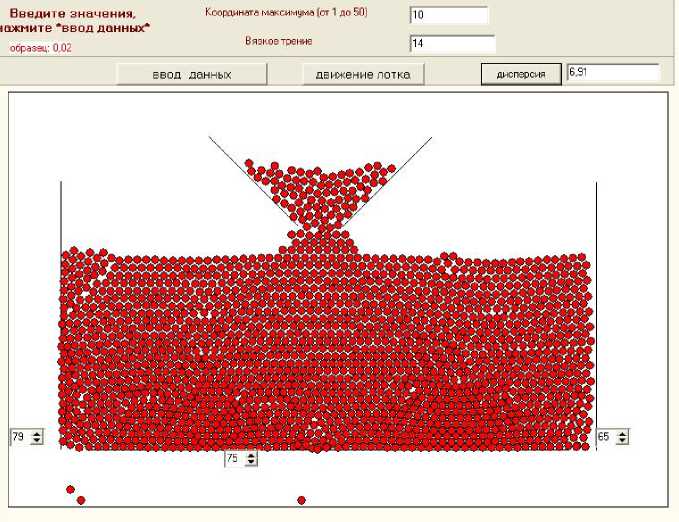
Смещение точки сопряжения
a
от центра при увеличении вязкости (рис. 3) дает эффект «встряхивания» и принудительного высыпания.
Рис. 3. Результаты эксперимента для несимметричной поверхности кулачка
Выводы
. Модель движения гранулированной среды в качестве сил взаимодействия предполагает упругие силы контактного взаимодействия между соседними частицами, силы трения между соседними гранулами, стенками и дном и вязкие силы, введенные по аналогии с жидкими средами [3]. Эти вязкие силы достаточно реальны и характеризуют влажность рассматриваемого объема. В модели вязкие силы необходимо вводить для корректного численного решения задачи. Так как задача Коши, возникающая в данном случае, является достаточно жесткой, собственные числа оператора перехода чисто мнимые. В этом случае даже энергетически согласованная схема Рунге-Кутта второго порядка, используемая в работе, недостаточно обеспечивает численное решение искусственной, вычислительной вязкостью. Поэтому введение физической, релеевской вязкости хорошо стабилизирует численное решение.
Интуитивно понятно, что «встряхивание» будет малоэффективным, если вязкость достаточно велика. Ожидать повышения высыпаемо-сти можно при сухих гранулированных средах. Однако выбирать вязкость очень малой или вообще нулевой нельзя из-за необходимости корректного численного решения задачи для жесткой системы обыкновенных дифференциальных уравнений. Разумный компромисс находится только при множественном вычислительном эксперименте. По результатам экспериментов сделаны следующие выводы. Для вязкой среды наибольшая равномерность высыпания гранул реализуется при колебании лотка, близком к гармоническому, что соответствует форме симметричного кулачка. Несимметричная форма кулачка, приводящая к резкому сдергиванию лотка, убирает застойные зоны вблизи отверстий в дне, возникающие из-за арочного эффекта, обусловленного сухим трением.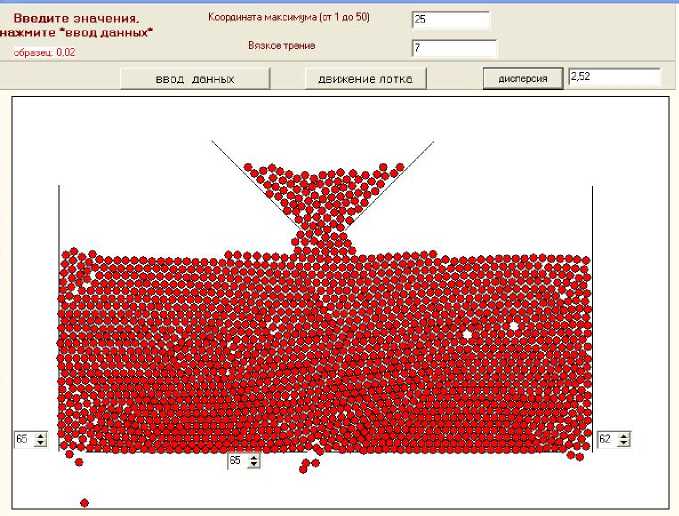
Список литературы Моделирование формы кулачка, обеспечивающей оптимальную работу высевающего устройства вибрационного типа
- Богульская Н.А., Богульский И.О. Числен-ное моделирование движения гранулиро-ванной среды в подвижных сосудах//Вы-числительные технологии. -2011. -№ 2. -С. 27-34.
- Богульский И.О., Богульская Н.А. Модели-рование движения неоднородной гранули-рованной среды с гранулами неправильной формы//Вестник КрасГАУ. -2012. -№ 11. -С. 41-49.
- Богульская Н.А., Богульский И.О., Вишня-ков А.А. Моделирование поведения гранулированной среды. -Красноярск, 2013. -90 с.
- Квасов Б.И. Методы изогеометрической аппроксимации сплайнами. -М.: ФИЗМАТ-ЛИТ, 2006. -360 с.


