Моделирование фронта ударной волны при сгорании стехиометрической смеси "горючее-окислитель"

Теория ударных волн достаточно подробно разработана, и описана, в литературе [1, 2], однако поиск аналитического решения для сферической волны в ряде случаев представляет проблему. Одномерный аналог рассматриваемой задачи называется ударной трубой и его решение известно [2]. Решение сферического случая представляет собой определенный интерес и имеет множество прикладных применений. В частности, знания параметров взрыва, газа, позволяют разработатв безопасные ГОСТы и нормативы для строительства помещений, в которых происходит работа, с горючими смесями.

Так же определенное прикладное значение имеет задача, об объединении множества, сферических взрывов в один цилиндрический и получение таким образом линейного взрыва, например, для взрывных работ в горном деле или для тушения крупного очага, возгорания.

«Московский физико-технический институт (национальный исследовательский университет)», 2022

2.    Модель ударной трубы и волны разрежения

Ударная труба представляет собой трубу, в которой перегородка разделяет две области, давление в одной из которых (на рис. 1 в левой) много болвше давления в другой. Когда перегородка мгновенно убирается, газ в области с высоким давлением начинает расширяться. Однако расширение просиходит не во всей области высокого давления, посколвку скорость звука и, следовательно, скорость передачи механического взаимодействия в газе конечны. Распространение в обратном к направлению распространения волны сжатия расширяющейся области газа высокого давления называется волной разремсения. При этом макропараметры среды при прохождении через волну разрежения, в отличие от волны сжатия, не могут меняться скачкообразно, то есть ударная волна разрежения невозможна.

Учет волн разрежения в сферическом случае значительно усложняет задачу нахождения аналитического решения, поэтому в рассматриваемой модели принято допущение, что расширяется одновременно вся область повышенного давления, не имея различий в плотности. Справедливость такого предположения будет рассмотрена ниже.

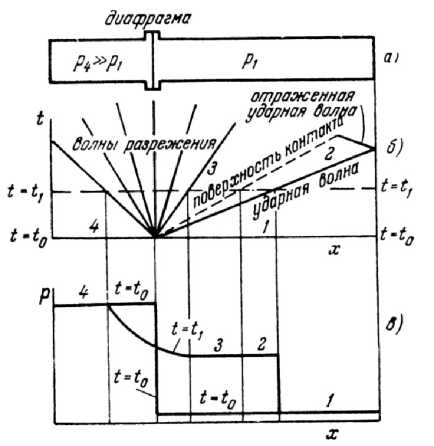
Рис. 1. Ударная труба: а) установка; б) распространение фронтов сжатия и разрежения во времени; в) профили давления в моменты времени t 1 и t o

3.    Теоретическая модель3.1.    Уравнение движения волнового фронта

Считаем, что реакция горения протекает во всей области много быстрее расширения области.

Предполагая, что плотность продуктов горения однородна, и пренебрегая толщиной фронта сжатия, записываем второй закон Ньютона для сжимаемого взрывом окружающего воздуха:

(Р(V ) - P^S =

- V^pg-O) dt

Если область с газом - сфера, цилиндр или плоскость, то dV = Sdr, где S - площадь поверхности области, поэтому

где Р_а - атмосферное давление, Vg - начальный объем газа, р_а - плотность окружающего воздуха, у - показатель адиабаты газа.

Считаем расширение газа адиабатическим, тогда уравнение адиабаты Р(V ) = Pg (Щ)⁷ подставляем в (1). Получившееся дифференциальное уравнение (Д.У.) решим относительно V (г):

V

2Ро Vg ⁷    V ^2-7     V^1-7         Ра

Ра (V -Vo )² V² — У ⁰ 1 -7⁺ ) ра '

Здесь С - константа интегрирования. Для существования конечного решения в начальный момент времени разложение множителя Щ - у — Vo Щ-7 + С в ряд Тейлора по V вокруг точки Vg должно иметь равные нулю нулевой и первый члены. Первый член равен нулю тождественно: Vg^1-7 — Vg Vg ^-7, а из равенства нулю нулевого члена можно найти константу интегрирования: С = _(2-^Щ ⁰ _-7) •

А если взять разложение вышеупомянутого множителя до второго порядка, то можно найти скорость в начальный момент времени:

I Pg — Ра " ⁽’°) = V ""Р^-'

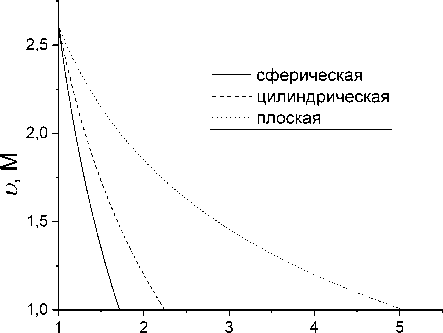
Таким образом, получена зависимость скорости расширения фронта волны от радиуса фронта, показанная на рис. 2а:

V (г )

2Ро г° ⁸⁷

Ра (г⁸ — Г о ⁸ )2

_г$^(2-7)       _г^8(1-7 )         _{Г о} ^8(2-7)    \     Р_а

^{2 —} У    ^Г° ^{1 —} У ^{+ (2 —} У^{)(1 —} У)7    Ра '

где s - параметр: 1 - для плоскости, 2 - для цилиндра, 3 - для сферы, г ° - начальный размер области с газом, Pg - начальное давление газа.

Зависимость радиуса фронта от времени можно найти, решив Д.У. (2) относительно r(t) Численное решение методом Рунге-Кутты 4 порядка приведено на рис. 26.

Пг0

б)

Рис. 2. Решение для стехиосмеси пропан-воздух при начальном радиусе г0 = 1 м: а) зависимость скорости ударной волны от радиуса её фронта, б) зависимость радиуса фронта от времени

а)

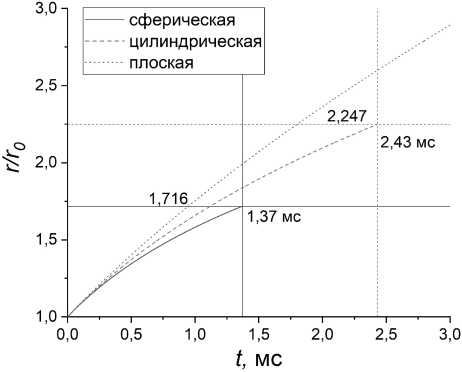
Переход ударной волны в акустическую произойдет, когда скорость фронта упадет до скорости звука. Радиус фронта, при котором это произойдет, назовем критическим. Неявную зависимость критического радиуса от начального г_к Дг° ) можно получить, положив в формуле (2) V = с, г = г_кр. График данной зависимости приведен на рис. 3.

Как видно из графика, решениями являются прямые пропорциональности. Найдем их явный вид, подставив в г_к Дг° ) прямо пропорциональную зависимость:

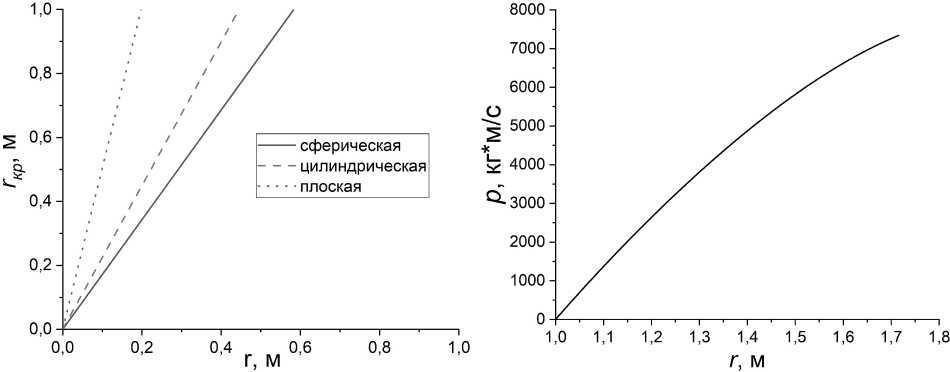
Рис. 3. Зависимость критического радиуса от начального

Рис. 4. Зависимость импульса от радиуса сферического фронта, г0 = 1 м гкР = Ух^о •

Решив получившееся степенное уравнение на % численно, для стехиосмеси пропанвоздух получим % = 5.048.

Тогда, в частности, для сферы получаем г_кр = 1.716tq, что согласуется с экспериментальным результатом 1.7го [3].

Зная скорость, можем найти зависимость импульса от радиуса фронта. Её график приведен на рис. 4.

3.2.    Макропараметры продуктов горения и фронта сжатия сферической ударной волны

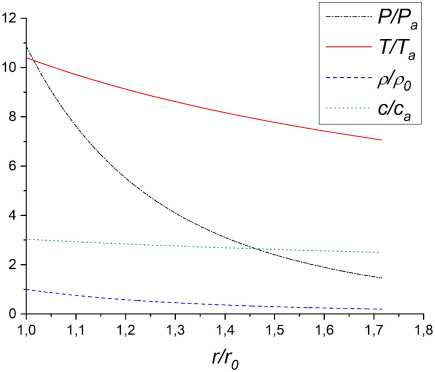
Для дальнейших рассуждений имеет ценность посчитать макропараметры расширяющихся продуктов горения и фронта сжатия. Поскольку мы считали расширение продуктов горения адиабатическим, мы можем найти макропараметры просто из уравнения адибаты идеального газа ( PV^ = const или TV^ -1 = const). Их графики приведены на рис. 5а.

Давление во фронте сжатия такое же, как и у продуктов горения. Для нахождения оставшихся макропараметров фронта сжатия достаточно знать еще один, например плотность, которую можно получить из уравнения ударной адиабаты для идеального газа [1]:

_{п т = п} (7 + 1)P(V) + (7 - 1\Рд

Рф( ) Ра (7 - 1)Р(V) + (7 + 1)Ра ’ где рф - плотность фронта сжатия.

Графики макропараметров фронта сжатия приведены на рис. 56.

3.3.    Оценка сделанных допущений

Помимо идеальности газа, адиабатичности расширения и отсутствия диффузии продуктов горения в фронт сжатия окружающего воздуха сделано еще два принципиально важных допущения: мы пренебрегли волной разрежения и размерами фронта сжатия.

Приведем сначала обоснование пренебрежения объемом фронта сжатия. Для этого вычислим его толщину К (макропарамтры фронта, в том числе и плотность, были найдены из (3) в предыдущем пункте):

а)

Рис. 5. Макропараметры системы: а) продуктов горения, б) фронта сжатия

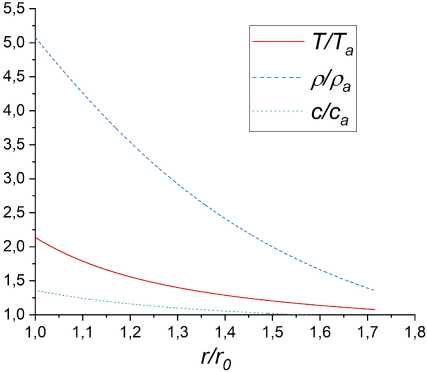
б)

Линеаризуем левую часть по Аг и получим следующую формулу:

Аг - т» г (1 - (г⁰)³) •

Высчитав по этой формуле толщину, получаем, что при г — г_кр толщина составляет 20% от критического радиуса. Если не применять линеаризацию, а решить кубическое уравнение (4), то получим Аг_кр — 0, 17г_кр. Как видим, толщина все время движения мала по сравнению с радиусом, поэтому наше пренебрежение обосновано.

Пренебрежение волной разрежения может быть обосновано следующим образом: как видно из графика, скорость звука внутри газа из продуктов горения падает медленно, изменяясь в пределах от 3 до 2,5 Махов. Такое медленное спадание обусловленно тем, что температура спадает как V ^1-7, а скорость звука как корень из температуры. При этом полученная в нашей модели скорость волонового фронта спадает быстрее. Оценим, за какое время в расширение будет вовлечено 90% объема продутов горения: (г₀ — ct)³ — 0.1г3. Отсюда получим, что при го — 1м это время составляет порядка 0,5 мс, то есть около трети от времени всего расширения.

Физически данное допущение обозначает, что в начальный момент времени слои газа уже имели ненулевые радиальные составляющие скорости. Именно поэтому в нашей модели получается ненулевая начальная скорость. Однако в таком скачке скорости нет ничего противоестественного, поскольку это скорость волнового фронта, масса которого в начальный момент времени нулевая, поэтому импульс его также нулевой и не испытывает никаких скачков (рис. 4).

Получается, что это допущение накладывает на газ начальное условие в виде радиального поля скоростей. При сжигании покоящегося газа и в модели ударной трубы подобное начальное условие не выполняется. Однако в реальном процессе волна разрежения в определенный момент времени (оцененный выше) дойдет до центра шара и тогда мы получим задачу с начальными условиями, удовлетворяющими нашему допущению. Иными словами, произойдет сшивка решений двух разных задач: с волной разрежения и без волны разрежения. Пример сшивки решений двух разных задач будет разобран в пункте 5.

4.    Передача энергии ударной волны стене

Большой интерес представляет собой вопрос воздействия ударной волны на препятствия, в частности на стены строений. В данном пункте приведена оценка переданной стене энергии ударной волны, состоящей из кинетической энергии волны и работы газа над стеной:

Е — Е™ _н + А.

4.1.    Передача кинетической энергии

Сначала приведем известную [4] формулу для коэффициента передачи энергии акустической ВО.ЛНВІ при переходе из среды 1 в среду 2:

D

ак

4 Р1С1 • Р2С2 (рЮ1 + Р2С2 )2

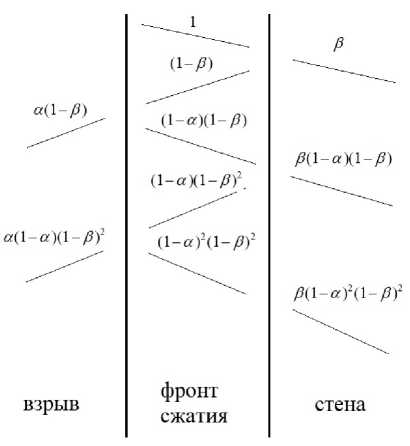
Рис. 6. Передача, и отражение энергии в системе взрыв-фронт-стена

Однако для ударной волны она. неприменима, посколвку вместо двух сред мы, по сути, имеем три: взрыв (продукты горения), фронт сжатия и стена. Кинетическая энергия фронта. сжатия по формуле (5) передастся стене, потом частв отразится обратно и из отраженной части частв отразится обратно в стену и т.д. (рис. 6). Значит, итоговый коэффициент передачи является суммой геометрической прогрессии:

• ^{3 + 3(1 -} а⁾⁽1 ^- 3) ⁺ /3(1 ^- а⁾²(1 ^- 3⁾² + ... —   —- — ^D_yд(К).

a + р - ар

Здесь а — a(V ) и 3 — 3 (V ) - коэффициенты энергетического пропускания на границах взрыв-фронт и фронт-стена, соответственно, вычисляемые по формуле (5). Нахождение скорости звука и плотности взрыва и фронта сжатия описано в пункте 3.2. Таким образом, получаем итоговую формулу для передачи кинетической энергии ударной волны:

Е -^кин

(г) — {

Dy?1EKо(г),г 6 гкр D^E.щ(гкр),г>гкр , где Е^о — 2ptt(V - Vq)h2(V) - собственная кинетическая энергия ударной волны.

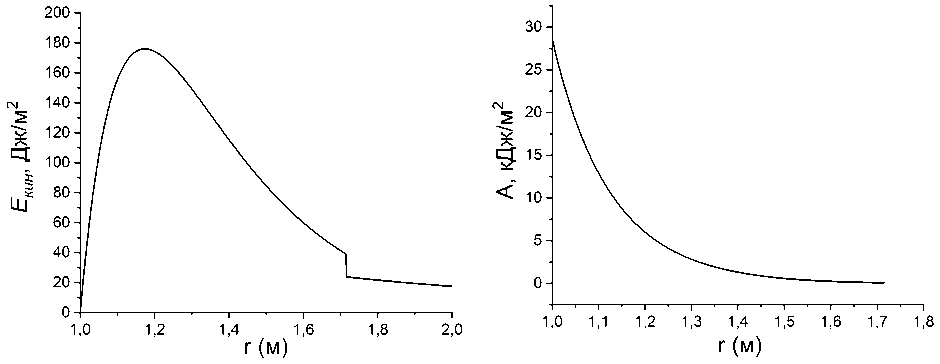
Полученная по этой формуле кинетическая энергия, передаваемая однослойной кладке силикатного кирпича [5] волной с начальным радиусом 1 м, приведена на рис. 7а.

4.2.    Работа расширяющегося газа

Помимо передачи кинетической энергии, расширяющийся газ может совершать работу над стеной. При этом работа расходуется на преодоление сил упругости изгиба и сжатия стены:

А = Асж

+ Лизг.

Рассмотрим стену с жестко закрепленными краями толщиной Z, высотой Д, площадью S и модулем Юнга Е.

Оценим работу на сжатие. Для этого запишем закон упругости [6], считая что расширение закончилось из-за уравновешивания давления газа и механического напряжения стены:

Р(V) - Ра = Е—, где AZ - изменение толщины вследствие её сжатия газом.

Взяв определение работы: А = J Fdx, найдем выражение для работы сжатия:

Ас »(V ) = SEI (Р (V ) - Ра )2 .

Теперь оценим работу на изгиб. Закон упругости:

Ах =

(Р — Ра Ц3 192EI

где Ах и I - величина прогиба центра стены и момент инерции поперечного сечения стены соответственно.

Аналогично работе сжатия найдем работу изгиба:

Аиз r(V) =

(Р (V) - Ро)² Һ4S (V) 32Е13

Подставив (7) и (8) в (6), получаем окончательное выражение для работы газа над стеной. Её вид для силикатного кирпича и начального радиуса в 1 м приведен на рис. 76.

б)

а)

Рис. 7. Энергия, передаваемая единице площади стены из однойслойной кирпичной кладки взрывом стехиометрической смеси пропан-воздух с начальным радиусом 1 м: а) кинетическая; б) работа расширяющегося газа

4.3.    Оценка энергии ударной волны и минимизация её возможного урона

Вне окрестности точки перехода ударной волны в акустическую работа изгиба на 1,5-2 порядка болвше кинетической энергии, передаваемой стене и на 3 порядка больше работы сжатия, график суммарной энергии практически совпадает с графиком работы изгиба. Значит, что передаваемая энергия практически полностью определяется разницей давлений. Исходя из экспериментальных данных об энергиях разрушения для стен разных материалов [5] и сравнивая с нашими значениями, получаем, что ударная волна от стехиометрического облака пропан-воздух радиусом 1 метр разрушает кладку из одного кирпича, однако железобетонная плита такой же толщины (12 см) выдерживает взрыв, поэтому в случае такого взрыва бетонные перекрытия пола и потолка останутся целы, в отличие от стен.

Особую опасность в плане возможного взрыва представляют кухонные помещения. Основываясь на полученных данных о критическом радиусе, можно предложить безопасную схему размещения газового оборудования: оно должно отстоять от стен на расстояние, большее 1.71 максимального радиуса распространения газа, допускаемого системами вытяжек. Расстояние до пола и потолка не столь важно, поскольку они состоят из бетонных плит, а не из кирпичной кладки. Реализовать такие системы вытяжек в квартире затруднительно, но в промышленных помещениях или больших кухнях заведений общего питания можно, создавая карманы из металлических перегородок и устанавливая на них систему вентиляторов, постоянно обеспечивающих замещение воздуха внутри этих карманов.

5.    Объединение сферических волн в цилиндрическую

Помимо всего упомянутого выше различные прикладные применения имеет задача объединения множества сферических ударных волн в цилиндрическую.

Наша модель решает и цилиндрическую, и сферическую волны. Более того, на момент объединения сферических в цилиндрическую начальное условие (начальное поле радиальных скоростей) автоматически выполняется, поэтому применение данной модели к цилиндрической волне корректно.

Рассмотрим случай одинаковых сферических зарядов, центры которых расположены на одной прямой на расстоянии L >  2т_кр друг от друга (рис. 8).

Пренебрегая толщиной фронта сжатия ударной волны, можем использовать следующую модель: газ расширяется по сферическому закону, при этом объем в пересечении двух сфер вытесняется наверх так, что объем внутри огибающей равен суммарному объему сфер (на рис. 8 это означает равенство объемов вращения от площадей левой и правой штриховки). При этом площадь вращения в каждый момент времени должна быть минимальной, так как работа пропорциональна площади и работа должна быть минимизирована на всем пути.

Таким образом, получаем изопериметрическую задачу - минимизация площади вращения при равенстве объемов вращения:

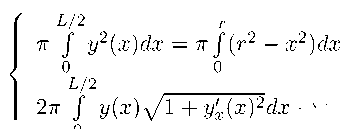
L/2

L/2       ___________

2тт j у(хЦ/1 + у)(х)² dx ^ min

Здесь у(х) - уравнение огибающей объединенного фронта. Оставим решение данной изопериметрической задачи за рамками рассмотрения данной статьи, нас интересует момент, когда сферическая модель переходит в цилиндрическую. Это происходит при ri = 4 L, когда при достижении радиусом фронта сжатия величины щ кривая у(х) вырождется в прямую:

4 7ГГ

= ТГГ2 L.

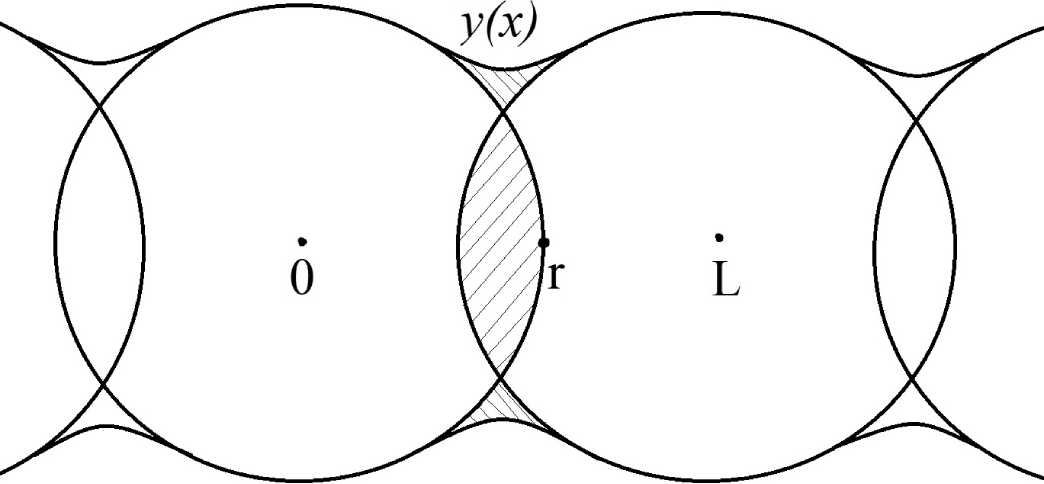
Рис. 8. Объединение сферических волн в цилиндрическую. Объемы вращения площадей правой и левой штриховки равны

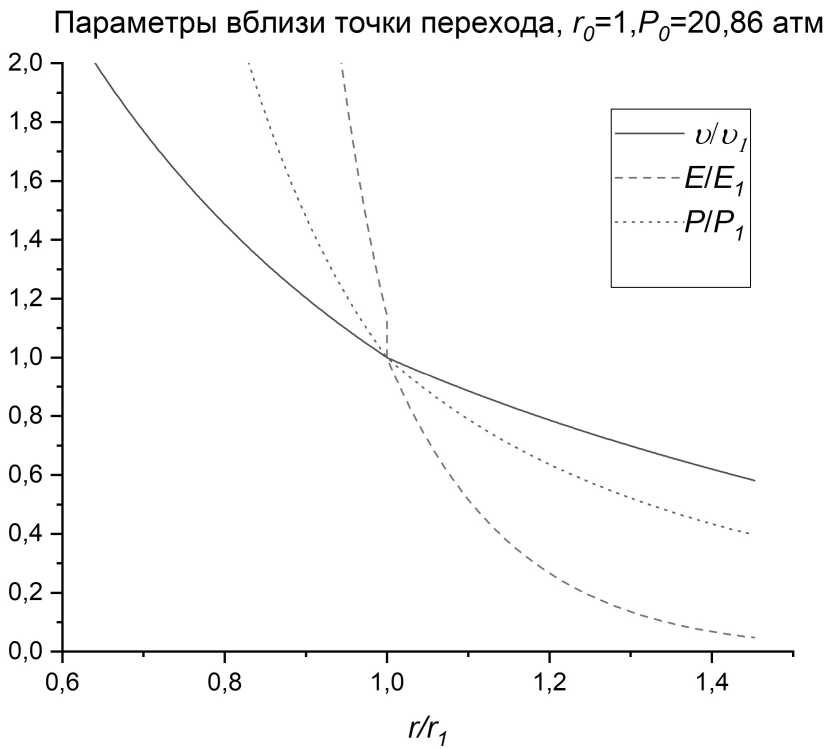
Рис. 9. Отношение параметров взрыва к их значеням в точке сшивки: скорости; энергии, передаваемой единице площади стены; давления

Сшивку двух решений проведем следующим образом: имеем решение для сферы, которое достигает ri. Как только это произошло, берем за начальные условия для новой задачи Коши и(11) = D1 ,r(t1) = r1. Новое дифференциальное уравнение получим, подставив в (1) Р (V) = Р1 (^1 }75 г де Pi = Р (r1), V1 = V (r1). Айалогично Т1 = Т (r1), р1 = p(r1) (правда, эти величины мы переписали лишь ради удобства, поскольку они высчитываются из объема и давления). Получаем почти идентичное с (1) Д.У.:

Р1 (У Г - Ра = 2 + (V-V) dv²

Pa         ^       2 dV , решением которого является

v

2 н

2РУ   /V²"7  , V 1^-^ ₍ _\  Ра

Pa(V - Vo)² V^{2 -} 7    ^{0 1 -} 7     ) Pa ‘

Заметим, что если положить Pi = Ро и Vi = V0, то новое решение совпадет со старым.

Только теперь константу интегрирования находим из условия vH(Vi) = щ.

Таким образом, можно сшить решения, причем не только при объединении сферических волн в цилиндрическую, но также цилиндрических в плоскую. График макропараметров при объединении сферических в цилиндрические показан на рис. 9.

Корректность сшивки проверяется в том числе сшивкой сферического решения со сферическим в произольной точке (при этом непременно получается то же решение).

6.    Заключение

В работе получены следующие результаты.

Пренебрегая волнами разрежения и размерами волнового фронта (что эквивалентно требованию на начальное радиальное поле скоростей), выведено уравнение движения сферического, цилиндрического и плоского волнового фронта, получены макропараметры термодинамической системы. Для сферической волны проведена оценка уместности сделанных допущений.