Моделирование гидродинамического воздействия на подводный газопровод в траншее с разжиженным грунтом

Как показывает практика эксплуатации объектов нефтегазовой промышленности, подводные переходы являются наиболее аварийно опасными в системе магистральных трубопроводов [1–3]. Экстремальное гидродинамическое воздействие поверхностных волн на подводный переход приводит к разжижению грунта вокруг подводного газопровода и является одной из причин его выхода из строя.

Податливость трубы в разжиженном грунте увеличивается вследствие ослабления контакта с грунтом, что снижает собственную частоту изгибных колебаний подводного перехода. Совпадение собственной частоты с частотой гидродинамического воздействия может привести к резонансным колебаниям трубы и, как следствие, к аварии на подводном переходе.

Экспериментальные данные показывают, что грунт под интенсивным повторяющимся гидродинамическим воздействием переходит в разжиженное состояние за довольно короткое время, которое может составлять десятки характерных периодов волнения [4–5]. Существующие модели учитывают гидродинамическое воздействие на трубу, частично или полностью погруженную в грунт [6, 7]. При этом не

рассматривается дальнейшее состояние трубопровода, находящегося в разжиженной среде под действием интенсивных гидродинамических нагрузок.

В данной статье предложен мультидисциплинарный подход, позволяющий рассматривать колебания трубы с учётом её взаимодействия с окружающей жидкостью. Цель работы — создание расчётной модели колебаний трубопровода в разжиженном грунте и её исследование, которое включает анализ влияния параметров модели взаимодействия трубы и разжиженного основания и сопоставление собственной частоты пролёта трубопровода с частотой гидродинамического воздействия.

2.    Постановка задачи

Рассмотрим задачу гидродинамического воздействия стоячей волны на подводный трубопровод, не заполненный нефтепродуктом. На рисунке 1, а представлена схема задачи: на дне некоторого водоёма 1 находится прямая траншея с разжиженным грунтом 2 , в центре которой размещён трубопровод 3 . Обсудим двумерный случай, когда фронт стоячей волны ориентирован перпендикулярно оси трубопровода. Предположим, что пучность стоячей волны расположена над серединой траншеи. Возможность возникновения стоячей волны, локализованной в области протяжённой траншеи с массивным включением, показана в [8].

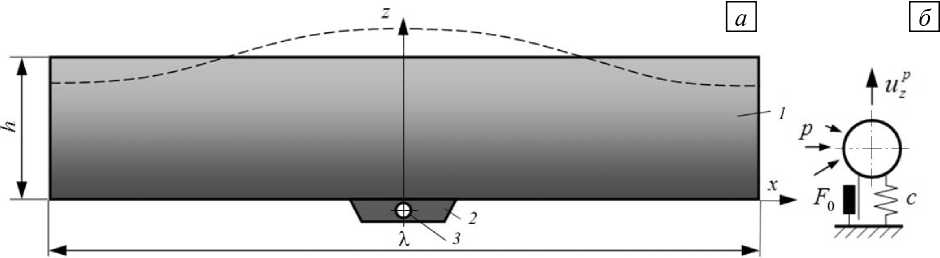
Рис. 1. Расчетная схема ( а ) и модель трубы ( б )

Вертикальные колебания подводного газопровода в разжиженном грунте будем исследовать с помощью параметрической модели. Для описания движения одного пролёта газопровода выберем представительное сечение, что позволяет рассматривать только низшую форму колебаний. Продольным силам в трубопроводе и реакциям со стороны грунта, действующим на сечение, поставим в соответствие реологическую модель, состоящую из параллельно работающих упругого элемента и элемента сухого трения (Рис. 1, б ). Первый из них соотносится с упругими перемещениями сечения трубы, второй — с рассеянием энергии при трении поверхности трубы о грунт. На рисунке 1, б обозначено: u_z^p — вертикальное перемещение трубы; F 0 — величина сухого трения; с — жёсткость упругого элемента; p — давление на поверхность трубопровода; x и z — оси координат. Пунктирной линией показана возможная форма свободной поверхности воды. На границе между жидкостью и трубой зададим условие контактного взаимодействия: u f • n = u p • n , где u f и u ^p — векторы перемещений жидкости и трубы.

Может показаться, что предложенная модель не отражает вязкие свойства разжиженного грунта, однако за счёт связи трубы с вязкой жидкостью модель автоматически приобретает вязкие свойства. Разжиженный грунт, представляющий собой взвесь частиц грунта в морской воде, опишем моделью «тяжёлой» жидкости.

Исходными гидродинамическими параметрами задачи являются глубина воды h = 20 м, амплитуда волн A = 3 м и период спектрального пика T0 = 10 c. Для удобства численного моделирования волнения воды ширина бассейна выбрана равной длине волн на мелкой воде для соответствующих параметров h и T0 [9]. Для указанных значений h и T0 корабельная скорость (скорость распространения уединённой волны с характерной длиной волны λ при глубине воды h) с0, длина волны λ и волновое число ξ , согласно теории волн на «мелкой» воде, имеют следующие значения: c0 = Jg ■ h = 14,0 м (g — ускорение свободного падения); X = c0T0 = 140 м; ^ = 2л/Х .

Движение воды в бассейне описывается уравнениями Навье–Стокса:

dv    / „ x „

P f gf ⁺ P f ^{(v Av) = V}

- pI + n((Vv ) + (Vv )T )

+ F ; V- v = 0,

где

p f = 1025 кг/м³ — плотность морской воды; v — вектор скоростей жидкости;

П = 0,001 Па ■ с — динамическая вязкость; F — вектор объёмных сил; I — единичный тензор; «Т» — знак операции транспонирования. Вода находится только под действием гравитационных сил, поэтому вектор объёмных сил имеет вид: F = -p f g k , где k — орт вертикальной оси.

Примем, что в начальный момент времени и жидкость, и газопровод неподвижны. Форму поверхности воды зададим кинематическим уравнением вида: up (x, z, t)| = A cos (Ex) sin (2nt]T0), где up — вертикальное перемещение частиц жидкости в направлении оси z; t — время. Давление на свободной поверхности положим без учёта атмосферной составляющей: p (x, z, t)| =0 = 0. На боковых гранях зададим условие симметрии — нормальная компонента скорости и касательные напряжения равны нулю: n ■ v = 0, т ■

- pI + n((Vv) + (Vv)T)

= 0, где n и т — векторы, нормальный и касательный к границе.

Будем считать, что на дне выполняется условие запрета скольжения и проникновения: v = 0.

Как правило, сечение газопровода, помимо стальной несущей трубы, состоит из антикоррозионного покрытия, бетонной оболочки, защитной оболочки и так далее. Но ввиду того, что в данной работе интерес представляет динамическое поведение трубы в целом, рассматривается круглое сплошное сечение диаметром 1,2 м. Плотность материала в сечении трубы p _p примем равной плотности окружающей жидкости p f для обеспечения нейтральной плавучести и отсутствия статического прогиба трубы.

Вертикальное движение сечения трубопровода как жёсткого целого описывается уравнением колебаний одномассовой системы с сухим трением:

mU p + F ₀sign ( й р ) + cu Z = k ■ ф p n dl - mg .

Здесь m — погонная масса трубы, равная m = p _pS , где S — площадь круглого сечения. Каждому конкретному случаю соотношения параметров c и m можно поставить в соответствие значение собственной частоты со = ^/ c/m . Горизонтальные перемещения трубы в силу симметрии нагрузки считаем отсутствующими: u x = 0.

Таким образом, труба связана с неподвижным основанием двумя элементами — упругим элементом с жёсткостью с , а также элементом сухого трения с силой сцепления F 0 . Такая постановка позволяет учесть изгибную жёсткость трубопровода, а также его взаимодействие с окружающим грунтом. В результате задача определения полей скоростей, перемещений, давлений в жидкости, а также вертикальной скорости и перемещения сечения газопровода сводится к совместному решению уравнений (1) и (2).

3.    Конечно-элементное моделирование

Численное моделирование нестационарной задачи выполнено в системе конечноэлементного мультидисциплинарного моделирования COMSOL Multiphysics. Движение

Рис. 2. Вид конечно-элементной сетки

жидкости и твёрдого тела описывается с помощью лагранжева подхода с использованием подвижных сеток. При этом решается связанная посредством граничных условий система уравнений теории упругости и гидродинамики. Свободная поверхность жидкости и граница между трубой и жидкостью являются подвижными.

Для решения системы линейных уравнений используется UMFPACK Direct-метод — несимметричный мультифронтальный метод с прямой LU-факторизацией разреженной матрицы [10]. Нелинейные дифференциальные уравнения решаются итерационным путем. Интегрирование уравнений по времени проводится с помощью явного метода Эйлера. Максимальный шаг по времени не превышает 0,1 c.

На рисунке 2 представлена конечно-элементная сетка для расчётной модели, которая имеет следующие характеристики: тип элементов — Лагранжа, квадратичные; форма элементов — треугольные; число узлов — 545; число элементов — 1014; число степеней свободы — 8757.

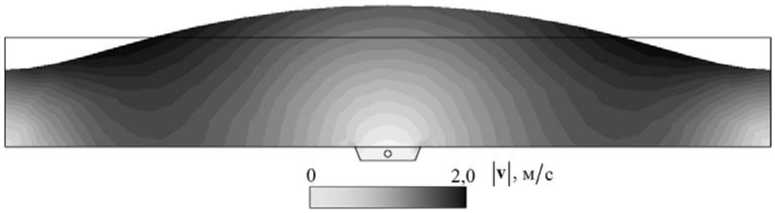
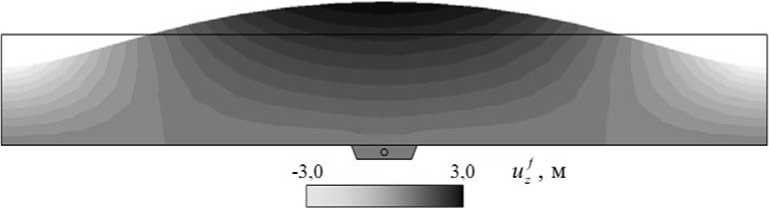
На рисунке 3 приведены, соответственно, поля скоростей жидкости, вертикальных перемещений и гидродинамического давления для характерного момента времени t = T ₀ 4 = 2,5c в выбранном представительном сечении.

а

б

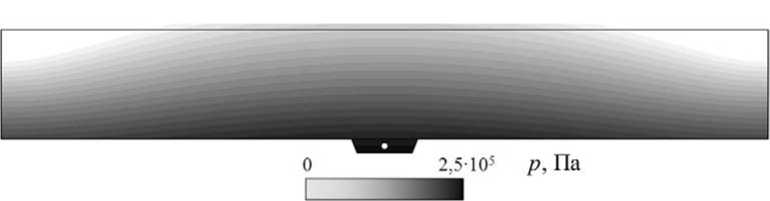
Рис. 3. Параметры жидкости в некоторый характерный момент времени: поле скоростей ( а ), поле вертикальных перемещений ( б ); поле гидродинамического давления ( в )

в

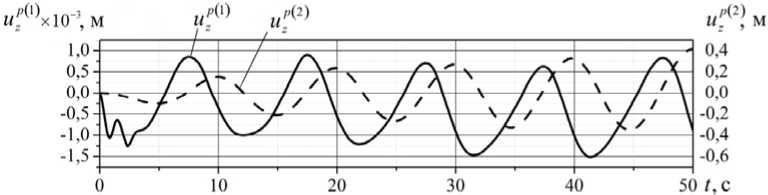
Рис. 4. Зависимости от времени вертикальной компоненты вектора перемещения сечения трубы u_z^p

для жёсткостей основания c ( 1 ) = 50 кН/м² и c ( 2 ) = 1 кН/м²

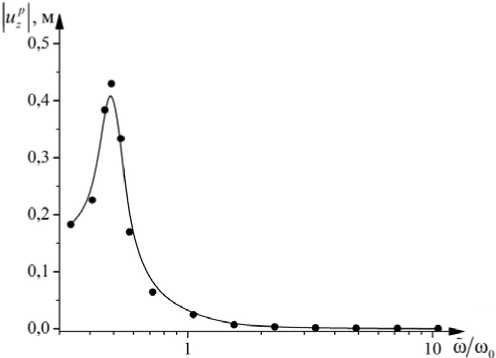
Рис. 5. Амплитудно-частотная характеристика системы без трения

На рисунке 4 показаны зависимости вертикальных перемещений u_z^{p (1)} ( t ) и u_z^{p (2)} ( t ) газопровода от времени на отрезке от 0 до 50 с для двух различных значений жёсткости основания: c ^{( 1 )} = 50 кН/м² и c ^{( 2 )} = 1 кН/м². Для обоих случаев величина силы сцепления составляет F 0 = 0 Н/м. Анализ приведённых зависимостей говорит о колебательном характере движения газопровода под действием стоячей волны. При первом значении жёсткости на отрезке времени от 0 до 5 с имеет место наложение свободных колебаний на вынужденные. Далее свободные колебания затухают и естественным образом выпадают из рассмотрения. Амплитуда вынужденных колебаний составляет 1 мм. Для второго значения видно нарастание амплитуды колебаний трубы, характерное для резонанса, при этом амплитуда колебаний составляет уже доли метра.

Рисунок 5 содержит амплитудно-частотную характеристику (АЧХ) для описанной модели без силы сухого трения. АЧХ построена по результатам нескольких численных экспериментов (на рисунке обозначены точками), в которых варьировалась жёсткость основания c . Сплошной линией обозначен сплайн, проведённый по данным 12 экспериментов. Пик АЧХ соответствует резонансу в системе «труба – движущаяся «тяжёлая» жидкость» при совпадении её собственной частоты с частотой гидродинамического воздействия.

Смещение пика резонанса в сторону более низких частот объясняется эффектом присоединённой массы. Так, для жесткости c = 1кН/м², плотности трубопровода р p = 1025 кг/м², равной плотности жидкости в траншее, отношение собственной частоты системы (2) к частоте гидродинамического возбуждения составляет

*w ω

ω0

cm )

12п/ T J

—J^ = 0,67.

Tc

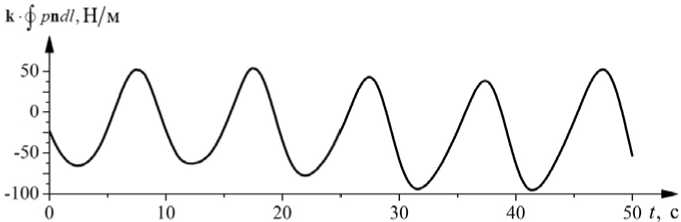
Рис. 6. Зависимость от времени действующей на трубу вынуждающей силы

Как показывает аналитическое решение [11], учёт влияния присоединённой массы «тяжёлой» жидкости в траншее приводит к повышению отношения 65/ю0 до значения, близкого к единице:

/^ ω

ω0

^f jcm )

1 2 я/ T o J

2п I p p S + p f n R²

T 0 c

= 0,96.

Таким образом, опираясь на формулы (3) и (4), можно проводить сравнение собственных частот, получаемых с помощью численного решения описанной выше модели и аналитического решения, в котором принимается во внимание присоединённая масса. Разница между результатами составляет не более 5%.

Для исследования влияния силы сухого трения на колебания трубопровода необходимо оценить также уровень гидродинамической нагрузки. В рассматриваемой модели действующая на трубопровод вынуждающая сила является неизвестной функцией и находится в результате решения связанной задачи. Зависимость вынуждающей силы от времени в уравнении (2) для случая неподвижного трубопровода при указанных параметрах глубины воды, амплитуды волн и периода возбуждения волн приведена на рисунке 6. Амплитуда колебаний повторяющейся нагрузки составляет 60 Н/м.

Параметр силы сухого трения F 0 играет важную роль в демпфировании колебаний газопровода, особенно при резонансе. На рисунке 7 представлена зависимость амплитуды колебаний трубы u_z^p от величины силы сцепления F 0 для резонансного случая при жёсткости основания c = 1кН/м² . Точками обозначены результаты конечного числа численных экспериментов, а сплошная линия отображает закономерность зависимости. Пунктирной линией множество точек условно разбито на две области: значениям F о е (0; 60) Н/м соответствует режим раскачки системы; при F о > 60 Н/м амплитуда колебаний трубы остаётся постоянной во времени.

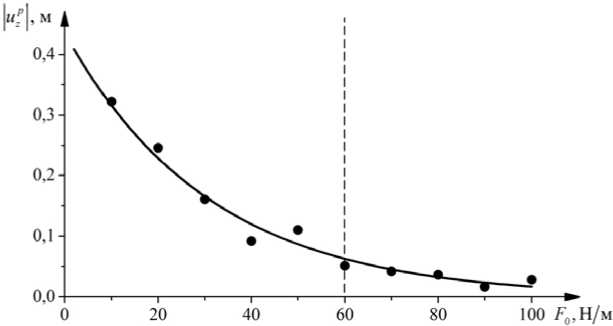
Рис. 7. Зависимость амплитуды колебаний трубы от величины силы сухого трения

4.    Заключение

Представлена двухмерная модель подводного газопровода в разжиженном грунте и численно решена задача его колебаний под гидродинамическим воздействием стоячей волны с заданными параметрами. Благодаря мультидисциплинарному подходу рассмотрена связанная задача взаимодействия трубы и «тяжёлой» жидкости.

Предложенная модель позволяет проводить многовариантные расчёты с целью исследования возможности наступления резонансных явлений подводных газопроводов, находящихся в траншеях с разжиженным грунтом.

Показано влияние параметров жесткости основания и силы сухого трения на колебания трубы, а также то, что различные соотношения параметров жёсткости и трения могут приводить как к управляемым колебаниям малых амплитуд, так и к резонансной раскачке газопровода.