Моделирование гидродинамики в испаряющейся из цилиндрической микроячейки жидкости с использованием приближения тонкого слоя и кинематического подхода

Капли и пленки, содержащие частицы вещества микро- и наноразмеров (наножидкости, полимерные суспензии, коллоидные растворы, биологические жидкости (размер частиц примерно от 1 нм до 1 мкм)), являются в последнее десятилетие предметом активных исследований благодаря многочисленным применениям в биомедицине, нанотехнологиях, печати, при нанесении покрытий [1]. Авторы [2] впервые выявили фундаментальный механизм эффекта «кофейного кольца» в сидячих (помещенных на твердую поверхность) каплях: скорость испарения на периферии этих капель больше, чем в центре, следовательно, при наличии закрепленной трехфазной границы жидкость–подложка–воздух возникает компенсационное течение, выносящее растворенное или взвешенное вещество к периферии капли, что приводит к образованию кольцевого осадка на подложке. Во многих технологиях этот эффект нежелателен, так как чаще требуется однородное осаждение на подложку.

На окончательном распределении частиц на подложке после полного высыхания капли раствора сказываются: динамика внутреннего потока в капле, кинетика испарения, динамика линии контакта (трехфазная граница), эволюция профиля капли, межчастичные и межфазные взаимодействия. Кроме того, система «капля–подложка» является открытой, всегда находится в неравновесном состоянии и

чрезвычайно чувствительна к условиям окружающей среды. Распределением частиц можно управлять с помощью различных факторов, в том числе сменой растворителя или материала подложки [3, 4].

Зависимость направления течения в капле, расположенной на плоской полидиметилсилоксановой подложке, от вида органической жидкости (метанола, этанола, изопропанола) авторы [5] объясняют существованием термокапиллярного эффекта Марангони. Численное решение уравнения теплопроводности показало, что, если теплопроводность подложки, по меньшей мере, в два раза больше, чем теплопроводность жидкости, то по линии контакта капля является самой теплой.

Испарение жидкостей, находящихся в ячейках, также привлекает к себе внимание в связи с новыми приложениями, например, в дисплеях на основе органических светодиодов. Для течения жидкости, испаряющейся из ячейки, свойственны те же основные процессы, что и для капель (пленок) на плоских горизонтальных подложках; возможны те же режимы испарения. Однако через некоторое время после начала испарения при соприкосновении поверхности жидкости с подложкой в центре ячейки образуется вторая трехфазная граница [6]. Авторы этой работы представляют экспериментальные данные по испарению этиленгликоля в цилиндрической ячейке микрометрового размера. В процессе испарения при комнатной температуре в жидкости наблюдается течение, направленное к краю ячейки. В [7] численно, с помощью метода функции уровня, рассмотрено влияние на испарение величины краевого угла смачивания и геометрии ячейки. В [8] экспериментально изучалось испарение жидкости из ячеек разных форм. Результаты сравнивались с данными численных расчетов по уравнению Лапласа для концентрации пара в атмосфере. Течения в нагретой чашке Петри численно и экспериментально исследовались в [9]. Авторы провели численный расчет в приближении Буссинеска течений в макроячейке на основе модели, учитывающей зависимость плотности жидкости от температуры. Количественное сравнение полученных численных результатов с экспериментальными измерениями скорости потока этиленгликоля в ячейке из [6] выполняется в [10], где модель описывает только усредненную по толщине жидкого слоя скорость радиального потока и учитывает лишь капиллярный поток жидкости. Тепловые эффекты вследствие малости градиента температуры вдоль свободной поверхности жидкости во внимание не принимаются.

Цель текущей работы заключается в модификации модели из [11] для возможности рассмотрения другой геометрии задачи, перехода от капли на подложке к жидкости в микроячейке, что позволит предсказать поле скорости потока в ячейке.

• 2.    Математическая модель

  • 2.1.    Физическая постановка задачи

На основании на данных эксперимента [6] рассмотрено испарение жидкости (этиленгликоля), размещенной в цилиндрической ячейке микрометрового размера. Ячейка выглядит как выемка размерами r w = 100мкм, h w = 6.13 мкм в горизонтально расположенной твердой непроницаемой подложке (Рис. 1).

Расчетная область ограничена параметрами r_s , h_s , h_a ; J — плотность потока пара в атмосферу .

В силу осевой симметрии объекта исследования и отсутствия зависимости свойств от угла вращения постановка задачи формулируется в цилиндрической системе координат O rz . Свободная поверхность жидкости имеет форму сферического сегмента [6] и с учетом того, что высота жидкости в центре ячейки h ( 0, t ) <<  r w , приближенно описывается функцией h ( r , t ) ® h ( 0, t ) ( 1 - ( r/r w ) 2 ) . Согласно эксперименту [6],

h ( 0, t ) = ( 7.38 - 0.042 1 ) мкм, где время

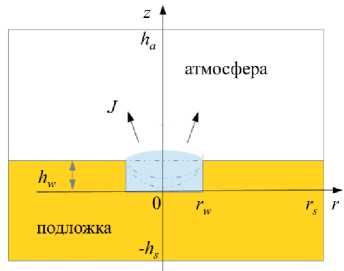
Рис. 1. Схема расчетной области к задаче испарения жидкости из ячейки; пунктирными линиями изображена свободная поверхность жидкости в разные моменты времени

t измеряется в секундах.

Испарение жидкости является свободным, трехфазная граница жидкость–подложка–воздух (верхний край ячейки) закреплена в течение всего процесса. В сформулированной постановке слой жидкости считается тонким до момента, пока его свободная поверхность не достигает дна ячейки, численные расчеты проводились до этого времени. Процесс испарения считается медленным (по данным эксперимента [6] жидкость сохнет tf та200 с). Температура подложки и жидкости в момент ее размещения в ячейке равна температуре воздуха T0 = 20 °С. Число Пекле для тепловых процессов в этиленгликоле много меньше единицы, Pe = ul/К®(10-7 -10-4)/10-7 ® 10-4 (здесь и — характерная скорость, которая по данным эксперимента не превышает 1 мкм/с; X — температуропроводность этиленгликоля, величина приведена в таблице ниже; l — характерный размер), поэтому теплопроводность доминирует над конвективным переносом тепла, который здесь не учитывается. Конвективные воздушные потоки, как и в [6], отсутствуют, поэтому в постановку не включаются, а потоки тепла из атмосферы не рассматриваются вследствие малой теплопроводности воздуха. При испарении жидкости происходит ее охлаждение, что приводит к неоднородному поверхностному натяжению и появлению дополнительного (термокапиллярного) потока вдоль свободной поверхности. Кроме этого, в результате испарения возникает компенсационный поток, который, по мнению авторов [6], в их эксперименте вносит наибольший вклад. Течение в ячейке ламинарное, жидкость несжимаемая (плотность р = const), вязкость ц = const.

• 2.2.    Основные уравнения модели

Для нахождения плотности потока пара J сначала решается уравнение Лапласа

A C p = 0

для концентрации пара C_p в атмосфере со следующими граничными условиями:

– на свободной поверхности жидкости концентрация равняется концентрации насыщенного пара, а вдали от жидкости она полагается нулевой (органическая жидкость);

– подложка считается непроницаемой для молекул пара испаряющейся жидкости.

Затем определяется поток пара на свободной поверхности жидкости: J = - D p ■ grad C p ( D_p — коэффициент диффузии молекул пара в атмосфере). Численный расчет проводится с учетом перемещения границы жидкость-воздух вследствие испарения (см. аппроксимацию h ( r , t ) в разделе 2.1).

При испарении жидкости происходит ее охлаждение вблизи свободной поверхности. Температурное поле в жидкости и в подложке рассчитывается с помощью уравнения теплопроводности:

дT/8t = Xi -AT , где X i — температуропроводность жидкости и подложки, где индексы l и s обозначают, соответственно, жидкость и подложку.

Задаются граничные условия:

– температура подложки вдали от ячейки, заполненной жидкостью, равняется температуре окружающей среды T ₀ ;

• - на оси симметрии O z радиальный поток тепла не существует, д T / дr = 0 ;

• – на верхней границе подложки с атмосферой в данной модели поток тепла полагается отсутствующим, д T / 8z = 0 ;

• - в нормальном к границе жидкость - подложка направлении n выполняется условие теплового баланса, д T / 8n = k_r д T_s (8n , где k_r = к _s /к l — отношение коэффициентов теплопроводности подложки и жидкости; - на свободной поверхности жидкости тепловой баланс подчиняется условию -к l д T B nn = LJ , где L — скрытая теплота парообразования.

Как и в [11], для расчета течения жидкости используется уравнение Навье–Стокса в приближении тонкого слоя с учетом напряжения на свободной поверхности жидкости, обусловленного зависимостью поверхностного натяжения жидкости ст от температуры. В этом приближении течение считается квазистационарным, ламинарным, жидкость полагается несжимаемой, внешние объемные силы не учитываются. Кроме того, если слой жидкости в ячейке тонкий, то допустимо принять давление в жидкости p и ее вязкость ц не зависящими от координаты z . Тогда в уравнении Навье-Стокса можно пренебречь малыми слагаемыми. В итоге получается следующее дифференциальное уравнение для радиальной компоненты скорости:

д ² V r ( r , z , t ) _ 1 д p ( r , t ) д z ²        ц д r

Интегрирование уравнения и учет условия прилипания жидкости ко дну ячейки ( z = 0 ) дает квадратичную зависимость радиальной компоненты скорости от координаты z : v_r = A ( r , t ) ■ z ² + B ( r , t ) ■ z ,

1 дp

где введено обозначение A ( r , t ) =-- . Из уравнения непрерывности div v = 0 следует:

2ц дr v = -— — (r ■ A(r,t))- — — (r ■ B(r,t)) . z    3 r дr(    ) r 2 r дr(    ) П

Неизвестные функции A ( r , t ) и B ( r , t ) определяются из дополнительных условий. Так, из баланса сил

_                                      ,     , х                        Г д v, 5v на свободной поверхности жидкости (z = h) получается, что ц —- +---

L дz дr дс д T               .

. Считая, что свободная д T д r

поверхность имеет малую кривизну ( h <<  r w ) вплоть до момента касания свободной поверхности жидкости дна ячейки, это условие можно переписать приближенно как

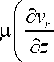
д r  J

8с 8 1 д Т д r ’

где v_z\_z=h = J / Р + д h/дt . Таким образом, в предлагаемой модели градиент капиллярного давления в явном виде не учитывается, а рассматривается некоторый компенсационный поток, порожденный неравномерным испарением со свободной поверхности (то есть к решению задачи становится возможным применение кинематического подхода). В модели зависимость поверхностного натяжения от температуры считается линейной и потому величина d с/ dT постоянна.

Еще одно условие для нахождения A ( r , t ) и B ( r , t ) следует из формулы для усредненной по высоте жидкости радиальной компоненты скорости течения [2, 11]

(v_r ) = — [( Az ² + BzAdz = —— rrJ ( r , t ) + p — Adr .

^{x rl} h 7          ' p rh ^J₀ L ^V         д t J

Окончательно получается:

A ( ^r , t ) =

3 r Г \   дh V   3 д2h   3 дJ   3 дс дT r I J (r, t) + p     I dr+

2 r ph3 0 L          дt J    4 h дtдr  4p h дr  4h ц дT дr х 3 r Г х    дhV   1 д2h

B ( , t ) = r J ( r , t ) + p dr ++ ^v ’     r p h ²0 L ^v ’    д t J     2 д t д r

1 д J 1 дсд T — 2 p д r 2 ц д T д r

Эти аналитические формулы для вертикальной и горизонтальной компонент вектора скорости потока v не учитывают условие прилипания жидкости к боковой стенке ячейки, а также условие отсутствия горизонтального потока на оси симметрии, поэтому для имитации выполнения этих условий в формулы добавлялась единичная ступенчатая функция Хевисайда.

Уравнение Лапласа для концентрации пара и уравнение теплопроводности решались методом конечных элементов с помощью пакета FlexPDE. Пакет позволяет выполнять численные расчеты в областях со сложной геометрией и подвижными границами. Размеры расчетной области были следующими (см. Рис. 1): r s = 5 r w , h s = 15 h w , h a = 10 r w , h s = 15 h w . Вычисления проводились до момента времени 0.9 t_touch , где t_touch — это время касания свободной поверхности жидкости в ячейке дна ячейки (согласно эксперименту [6], это время составляет ~144 с). Расчеты выполнялись для значений физических величин, приведенных в таблице.

Численный расчет плотности потока пара J для этиленгликоля в ячейке показал, что поток практически не меняется со временем и хорошо аппроксимируется формулой [10]:

Таблица. Значения физических величин в численных расчетах

Рабочая жидкость (этиленгликоль)

нас Концентрация насыщенного пара, C p	0.34·10–3 кг/м3
Коэффициент диффузии пара в атмосфере, Dp	1.1·10–5 м2/с
Плотность, p	1.11·103 кг/м3
Теплопроводность , к i	0.25 Вт м–1 град–1
Температуропроводность, X ।	1.1·10–7 м2/с
Теплота испарения, L	8.0·105 Дж/кг
Вязкость, ц	0.021 Па с
Температурный коэффициент поверхностного натяжения, d с/ dT	–9·10–5 Н м–1 град–1
Материал ячейки (диоксид кремния)
Теплопроводность, к 5	1.4 Вт м–1 град–1
Температуропроводность, X 5	8.3·10–7 м2/с

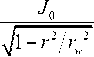
J      1 - exp ( - m J1 - r²/rw ² )

ф ( rlr ) = .    ⁰

w    1 1 - r 7 r w^{2        1 -} exp ^(- m )

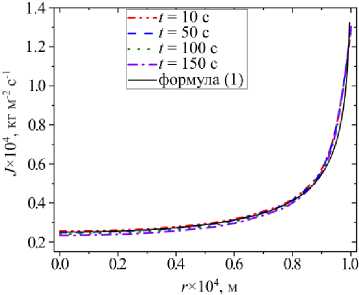
Рис. 2. Зависимость плотности потока пара J вдоль свободной поверхности жидкости в различные моменты времени; сплошная линия – модельный закон

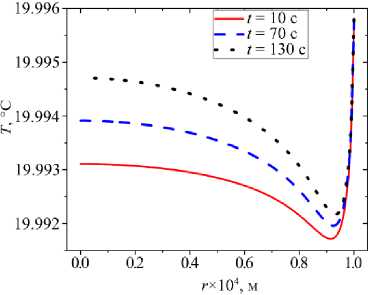
Рис. 3. Температура на свободной поверхности жидкости (этиленгликоля), находящейся в ячейке, в зависимости от радиальной координаты в различные

испарения (1)

моменты времени

при m = 7 и J 0 = 2.5 - 10 ⁵ кг м ² с ¹ (см. Рис. 2). В связи с этим для определения температурного поля и поля скорости течения использовалась функция (1).

На рисунке 3 представлена температура вдоль свободной поверхности этиленгликоля в разные моменты времени. Вычисления выявили, что в различные моменты времени разность температур на краю ячейки и в центре свободной поверхности этиленгликоля имеет порядок 10 - 3 -10 — 4 °С. Соответственно, течение Марангони, вызванное неоднородностью поверхностного натяжения, должно быть слабым. И эксперимент [6] это подтверждает. По мере испарения жидкости температура в центре свободной поверхности увеличивается. Так как жидкий слой в центре становится тоньше, то тепло от подложки передается к свободной поверхности быстрее. Максимальное испарение жидкости наблюдается на краю ячейки, как и в случае испарения капли на горизонтальной подложке. Однако вследствие того, что тепло от подложки поступает к жидкости не только от дна ячейки, но и от ее боковой поверхности и при этом диаметр ячейки существенно превышает ее глубину, температура на свободной поверхности жидкости в ячейке изменяется немонотонно.

Расчеты поля скорости по полученным аналитическим формулам представлены на рисунке 4 для двух моментов времени: t = 10 с и t = 90 с. На рисунке видно, что преобладает течение, направленное к краю капли, вызванное неоднородностью испарения. На рисунке 5 для различных моментов времени показаны результаты для усредненной по толщине жидкого слоя радиальной скорости потока v_r , которая, как оказалось, с течением времени возрастает.

В эксперименте [6] авторы наблюдали течения, направленные к краю капли, при этом максимальные скорости жидкости достигали примерно 0.5 — 1 мкм/с. По порядку величины результаты осуществленных вычислений согласуются с этими данными. Вблизи дна ячейки расчет по предложенной модели дает сложную картину течений, однако величина скорости у дна ячейки крайне мала, близка к нулю. Авторы [6]

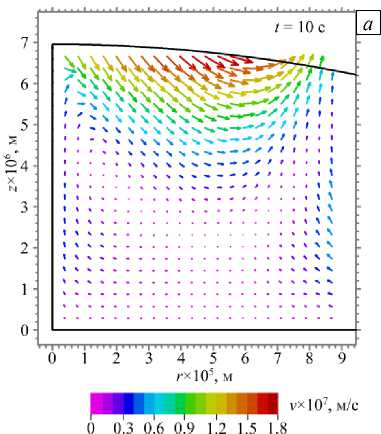
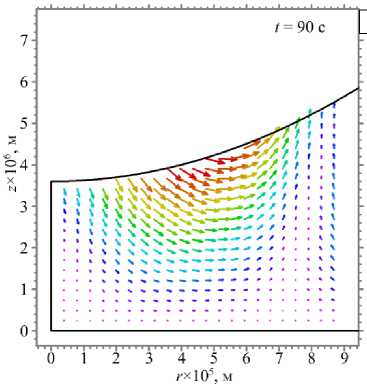
Рис. 4. Векторное поле скоростей течений в этиленгликоле, находящейся в ячейке, для моментов времени t , с: 10 ( а ) и 90 ( б )

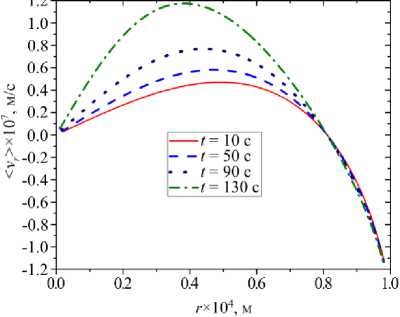
Рис. 5. Зависимость усредненной по толщине жидкого слоя радиальной скорости потока от радиальной координаты в различные моменты времени

отмечают проблематичность измерения скорости вблизи стенки и оси симметрии ячейки, поэтому сравнивать экспериментальные данные с расчетными в этих подобластях сомнительно. Используемая модель предсказывает вблизи стенки наличие течения в направлении центра ячейки. Расчеты по модели для частного случая, когда температурный коэффициент поверхностного натяжения принимается равным нулю, показывают уменьшение этого обратного течения.

4.    Заключение

Моделирование гидродинамики в микрообъемах позволяет предсказывать структуру потока, зависящую от различных физических параметров. Изучение структуры потока при неоднородном испарении вдоль свободной поверхности с учетом тепловых эффектов необходимо для задач испарительной литографии и других приложений [1]. Предложена модификация модели [11], базирующаяся на приближении тонкого слоя и кинематическом подходе.

В [11] авторы получили аналитические выражения вертикальной и горизонтальной компонент вектора скорости потока для случая сидячей капли. В текущей работе выведены аналогичные формулы для другой геометрии, а именно рассмотрена жидкость, испаряющаяся из цилиндрической ячейки. В модели учтены компенсационные и термокапиллярные потоки жидкости. Выполнен расчет для значений физических параметров, соответствующих эксперименту [6]. Полученные результаты качественно согласуются с экспериментальными данными [6]. Значение максимальной скорости потока этиленгликоля в ячейке по порядку величины совпадает экспериментальным [6].

Технические сложности не позволили авторам [6] наблюдать структуру потока вблизи стенки ячейки. Модель [10] не предсказывает наличие противотока вблизи стенки ячейки, так как в этой работе не учтен эффект Марангони. Предложенная здесь модель демонстрирует возникновение потока, направленного к центру ячейки вблизи ее стенки, что связано с градиентом температуры вблизи стенки ячейки, возникающим из-за испарения и отдачи тепла от ячейки к жидкости. Полученные аналитические формулы для расчета скорости потока жидкости в ячейке удобны в использовании, так как избавляют от необходимости численного расчета гидродинамики. Но, к сожалению, у них есть недостаток, связанный с проблемой учета граничных условий у стенки ячейки. В дальнейшем предполагается провести численный расчет скорости при тех же предположениях модели, чтобы уточнить границы применимости полученных аналитических формул.

Автор выражает благодарность К.С. Колегову, сотруднику Научной лаборатории «Математическое моделирование и информационные технологии в науке и образовании» АГУ им. В. Н. Татищева, за детальное обсуждение результатов работы.

Исследование выполнено за счет гранта Российского научного фонда (проект № 22-79-10216),