Моделирование городской инфраструктуры с использованием алгоритмов графов

Городская инфраструктура требует эффективного управления транспортными потоками. Основными задачами являются снижение пробок, оптимизация маршрутов и сокращение времени поездок. Графовые модели предоставляют мощный инструмент для анализа транспортных сетей, их визуализации и реализации алгоритмов поиска кратчайшего пути [1].

Цель данной работы – показать возможности графового моделирования городской инфраструктуры, а также продемонстрировать эффективность алгоритмов Дейкстры и A* на данных дорожной сети Москвы, предоставленных Open Street Map.

Методы и материалы:

Данные дорожной сети Москвы были загружены из Open Street Map (OSM) с использованием библиотеки OSMnx. Эти данные включают в себя информацию о перекрестках, дорогах, их длине и ограничениях скорости, что позволяет построить реалистичный граф дорожной сети.

Граф дорожной сети был построен с помощью OSMnx. Узлы графа представляют перекрестки или ключевые точки, а ребра – дороги с характеристиками, такими как длина и направление.

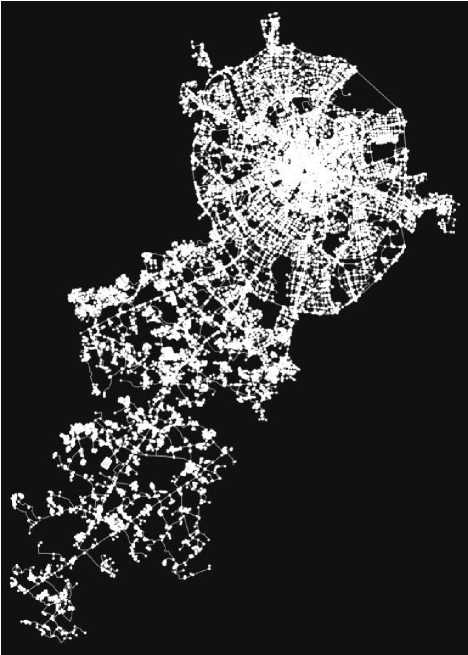
Рис. 1. Граф карты Москвы

Для поиска кратчайших путей в графе используются два классических алгоритма:

Алгоритм Дейкстры – этот алгоритм гарантирует нахождение кратчайшего пути от начального узла до всех других узлов графа. Его работа основана на пошаговом обновлении минимального расстояния для каждого узла, пока все возможные пути не будут исследованы. Такой подход делает алгоритм универсальным и надежным для задач, требующих точных решений. Однако вычислительная сложность Дейкстры увеличивается с ростом графа, что ограничивает его применение для очень больших сетей [2].

Алгоритм A* является усовершенствованной версией алгоритма Дейкстры. В отличие от последнего, A* использует эвристическую функцию, которая оценивает расстояние до целевого узла. Это позволяет алгоритму направлять поиск в перспективные области графа, сокращая число проверяемых узлов. Например, евклидово расстояние может использоваться как эвристика для оценки прямого расстояния до цели. Такой подход часто ускоряет выполнение, но точность и произво- дительность A* напрямую зависят от качества выбранной эвристики [3].

Визуализация работы алгоритмов

Для более глубокого понимания принципов работы алгоритмов Дейкстры и A* были построены маршруты в дорожной сети Москвы. На рисунке 2 представлен маршрут, найденный алгоритмом Дейкстры. Этот метод исследует все возможные узлы и находит оптимальный путь. Однако с увеличением размера графа сложность вычислений возрастает, что делает его менее эффективным для крупных дорожных сетей [4].

Рисунок 3 иллюстрирует маршрут, построенный с использованием алгоритма A*. Благодаря эвристической функции, алгоритм фокусируется на направлениях, которые с наибольшей вероятностью ведут к цели, что позволяет ему обрабатывать меньше узлов. Это значительно ускоряет выполнение поиска в графах с простой топологией. В данной работе использовалось евклидово расстояние в качестве эвристики, что показало высокую эффективность при маршрутизации в дорожной сети Москвы.

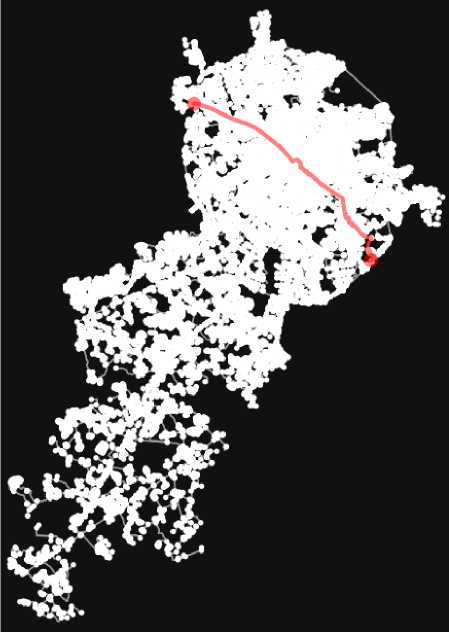
Рис. 2. Маршрут, полученный методом Дейкстры

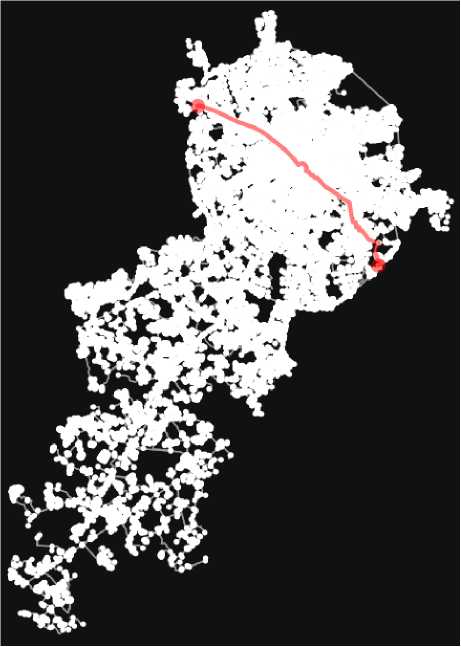
Рис. 3. Маршрут полученный методом А*

Анализ эвристики и ограничений

Эвристическая функция играет ключевую роль в производительности A*. В графах с ровной топологией (например, равномерное покрытие дорог) эвклидово расстояние позволяет находить маршруты быстро и точно. Од- нако в сетях со сложной структурой, таких как сети с большим количеством мостов или тоннелей, простая эвристика может приводить к неоптимальным результатам или дополнительным вычислительным затратам [5].

Кроме того, работа с данными Open Street Map выявила несколько типичных проблем:

Неполные данные: некоторые дороги могут отсутствовать, что приводит к разрывам в графе.

Шум и избыточность: графы могут включать элементы, не относящиеся к автомобильному транспорту (например, пешеходные дорожки).

Масштабирование: для крупных городов, таких как Москва, графы содержат миллионы узлов и ребер, что увеличивает требования к памяти и времени вычислений.

Метрики оценки

Для анализа алгоритмов был выбран маршрут от северо-запада до юго-востока Москвы. В сравнении эффективности алгоритмов использовались следующие метрики:

• -    Время выполнения: время, затраченное алгоритмом на поиск маршрута.

• -    Длина маршрута: общее число узлов в найденном маршруте.

Для удобного восприятия результаты были занесены в таблицу:

Таблица 1. Результаты двух методов поиска кратчайших путей

Алгоритм	Время выполнения (с)	Длина маршрута (узлы)
Дейкстра	0.0400	180
A*	0.0667	180

Анализ графа позволяет выявить узкие места в дорожной сети и предложить пути их устранения. Найденные маршруты могут быть использованы для планирования оптимальных путей с учетом длины дороги или времени поездки [6].

Использование графов и алгоритмов поиска пути представляет собой универсальный и мощный подход к моделированию и оптимизации городской инфраструктуры. Алгоритмы Дейкстры и A* продемонстрировали свою надежность и точность, эффективно решая задачу поиска кратчайшего пути. Несмотря на то, что алгоритм Дейкстры оказался быстрее A* в текущем эксперименте, A* предоставляет дополнительные преимущества за счет возможности использования эвристик, что делает его особенно полезным для более сложных задач или крупных графов. Результаты показывают, что такие методы способны не только минимизировать время поездок, но и стать основой для принятия решений в транспортном планировании, улучшая общую ситуацию в городах и повышая качество жизни их жителей.