Моделирование граничных условий при расчёте на прочность взрывных камер

Детонация газовой смеси в камере — это сложный физико-химический процесс, характеризующийся сверхзвуковым фронтом горения и резким увеличением давления и температуры [1–3]. Детонация происходит за счет самоподдерживающегося распространения фронта горения через волну сжатия, инициирующую химические реакции [4–6].

Детонация газовой смеси в камере является сложным и многофакторным процессом, который играет значительную роль в различных областях техники и науки. Исследования в этой области продолжаются с целью повышения эффективности и безопасности детонационных процессов [7–9].

1 Моделирование газовой детонации при предположении мгновенной детонации

Предполагается, что детонация газовой смеси происходит мгновенно, что соответствует допущению о бесконечной скорости распространения детонационных волн. Газовая смесь моделируется как идеальный газ, что позволяет использовать уравнение состояния идеального газа для определения давления во время детонации.

Кроме того, зависимость удельной теплоемкости газа от температуры моделируется кубической параболой, а уравнение регрессии строится на основе известных табличных данных для удельной теплоемкости в зависимости от температуры. Полученные зависимости давления сравниваются с известными данными из литературных источников.

Вывод основных уравнений

Давление, возникающее при детонации газовой смеси, можно определить с использованием уравнения состояния идеального газа:

P ( τ ) = ρ ^RT ,

(1.1)

γ где ρ, R, µ, T — плотность газовой смеси, газовая постоянная, молекулярный вес и температура смеси.

Для вычисления температуры газа воспользуемся законом сохранения энергии, который можно записать в следующем виде. Исходя из первого закона термодинамики и определения теплоемкости получаем:

dU = C_v ( T ) dT .

(1.2)

Здесь U — внутренняя энергия газа, C_v ( T )— его теплоемкость при постоянном объеме.

Тепловой поток, выделяющийся в процессе детонации, можно выразить через следующую зависимость [10]:

Q ( τ ) = Q 1 (1 - θ ) e ^{- k 1 τ} + Q 2 e ^{- k 2 τ} ,                        (1.3)

где Q ₁ , Q ₂ , θ , k ₁ , k ₂ — постоянные коэффициенты, зависящие от геометрических параметров камеры, состава газовой смеси и начального давления.

Изменение внутренней энергии газа dU равно количеству тепла, распределенного по внутренней поверхности камеры:

dU =- Q ( τ ) Sd τ .                       (1.4)

Здесь S — полная площадь внутренней поверхности камеры, τ — время, Q ( τ ) — тепловой поток из уравнения (1.3). Подставляя (1.2) и (1.4), получаем:

T τ

∫Cv(T)dT=-S∫Q(τ)dτ.(1.5)

Tv 0

Для удобства расчетов приближенные значения удельных теплоемкостей газа в зависимости от температуры можно аппроксимировать кубической параболой:

Cv(T)=aT3+Cv0,(1.6)

где a — постоянная, определяемая с учетом предельного условия, вытекающего из закона сохранения энергии:

Sτ∫Q(τ)dτ→mQC at τ →∞.(1.7)

Здесь m — масса газовой смеси, Q_C — удельная теплота сгорания. Поскольку при τ →∞ температура газа стремится к T → 0, из уравнений (1.2), (1.3) и (1.6) следует: 0

∫ ( a T ³ + C v 0 T v 0 ) dT ≈- mQ C ,                   (1.8)

T v 0

T_{v 0} — температура газовой смеси при мгновенном сгорании (для смеси, где T_D ≈ 4250⁰ K — температура в точке Чепмена — Куге). Используя (1.8), можно выразить:

mQ C - C v 0 T v ² 0 a = 4       ₄      .

T v 0

Далее, подставляя выражения из (1.2), (1.4), (1.4) и (1.6), получаем:

44τ a4T+Cv0T=aT4v0+Cv0Tv0-S∫Q(τ)dτ.

Решая это уравнение, находим зависимость T = T ( т ), а затем, используя (1.1), определяем зависимость P = P ( т ).

Для сравнения результатов были использованы зависимости удельных теплоемкостей газа от температуры, полученные в работе [11]:

Г, L ЕЕ1

• 1    +

Cv (Ц, T) = R    R' + B (Е) ,(1.9)

ц у - 1

⁽ Ц _та х ^- Ц ⁾⁽ Ц ^- Ц _т1П )

где B о              /\ .

• 2    Цах — 1Ц™ ( Ц + Цпах )

Затем сопоставляются зависимости P = P ( т ), найденные с использованием (1.6) и (1.9).

На рис. 1.1 представлены полученные результаты: сплошная линия показывает зависимость P = P ( т ) согласно данным из работы [11], а штриховая линия — аппроксимации удельной теплоемкости кубической параболой (1.6).

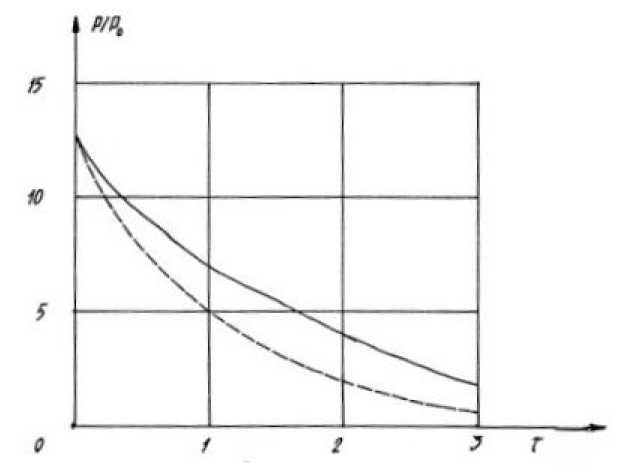
Рис. 1.1

Предполагая, что молекулярный вес газовой смеси остается неизменным ц = const , можно значительно упростить выражение для давления.

Плотность газовой смеси согласно уравнению состояния: p RTl

P 0           ,

Y где P0 — начальное давление, T0 — начальная температура газа. В таком случае уравнение (1.1) трансформируется в:

P Т ) = PT T

T 0

.

Имеем

РТ_П ’ = P (0) = PT ⁰ max V / гр

.

T0

Принимая T₀ = 293⁰ K , T v ₀ = 3 825⁰ K, можно вывести приближенную формулу, позволяющую оценить максимальное давление, возникающее при мгновенной детонации газовой смеси газов в заданном диапазоне давления:

• 1    = P (0) - 13 P 0 .

Таким образом, были разработаны приближенные выражения для расчета давления, возникающего на внутренней поверхности взрывных камер. В основу этих расчетов легла аппроксимация зависимости удельных теплоемкостей газа C v = C v ( T ) от температуры кубической параболой. Проведено сравнение полученных выражений с данными, представленными в научных источниках.

• 2    Моделирование газовой детонации с учетом конечной скорости распространения детонационных волн

В данной части рассматривается моделирование динамики изменения в камере с учетом конечной скорости распространения детонационных волн. В реальных условиях инициирование детонации чаще всего происходит на одном из концов камеры.

Процесс распространения детонационной волны представляется в модели в виде волны разрежения [1-3]. Слабые ударные волны, возникающие при отражении от торцевых стенок камеры, описываются одномерными бегущими с постепенно затухающей амплитудой. Коэффициент затухания подбирается таким образом, чтобы обеспечить соответствие расчетных данных результатам экспериментов как в количественном, так и в качественном аспекте.

Рассмотрим приближенную x , т диаграмму зависимости ( x — расстояние вдоль образующей камеры, т — время), иллюстрирующую распространение одномерных «акустических» ударных волн в камере. После инициирования детонации на левом торце камеры фронт детонационной волны распространяется вправо. Для углеводородо-кислородных смесей скорость фронта детонации D находится в пределах : 2 т 2,5 - 10³ м/с [11]. Перед фронтом детонации формируется область, в которой сохраняется постоянное начальное давление:

Р -Р

• ¹    I ¹ 0 ^.

Профиль движущейся волны детонации в определенный момент вре-

L 1

— I представлен на рис. 2.1.

мени

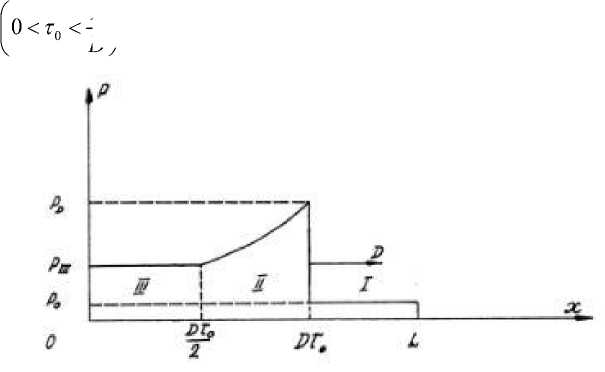
Рис. 2.1

На фронте детонационной волны давление претерпевает резкий скачок P D ~ kP₀. Для большинства газовых смесей величина k приближается к 40 [4]. За фронтом детонации формируется область разрежения (область II на рис. 2.1), где давление подчиняется следующему уравнению [11]:

2 Y

Р = [ Г-!*+11Y-1р PII “ I           + I PD ,

^ YD т у J причем у ~ 1,2 [1]. Волна разрежения, задний фронт которой движется со скоростью ^, оставляет за собой область покоя, характеризующуюся постоянным давлением PIII (рис. 2.1). Для определения давления PIII дос-DT таточно подставить x = в предыдущее уравнение. При принятых значениях параметров получаем PIII ~ 0,352PD. Данный результат по своей величине оказывается близким к давлению при мгновенной детонации P (т).

После отражения от противоположной стенки камеры возникающие ударные волны начинают распространяться в обратном направлении (рис. 2.2), двигаясь уже через продетонировавший газ со скоростью звука С , которая составляет приблизительно 1 ^ 1,4 • 10³ м/с. Со временем амплитуда этих волн затухает, причем степень затухания в первую очередь определяется количеством пробегов вдоль камеры [7].

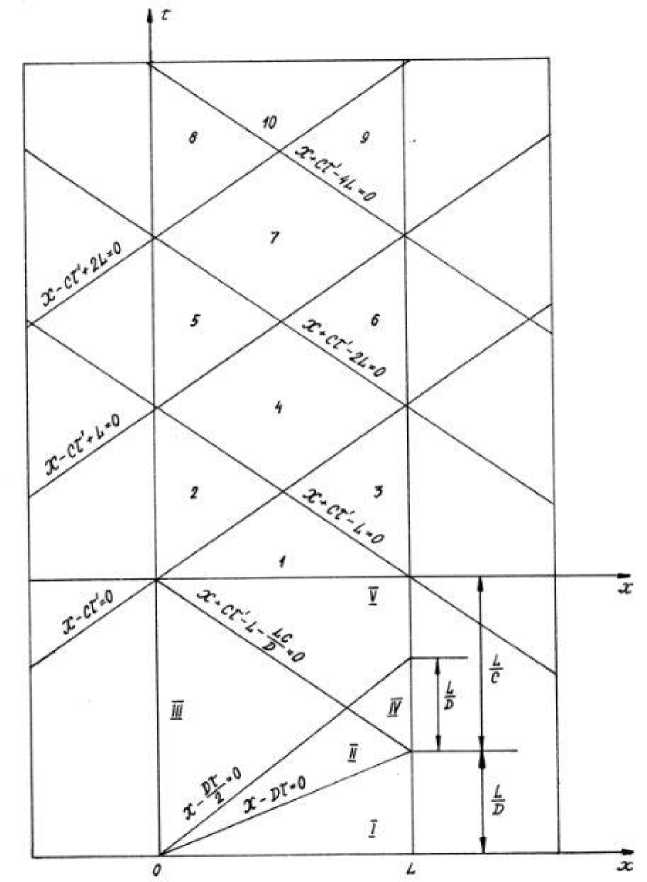
Рис. 2.2

Отраженная волна представляет собой бегущую волну, амплитуда ко торой постепенно уменьшается:

Р от = 1,5 P d • f ( Т ) •

2 L - x - C | т - L

I D

L

где L — длина камеры.

с I t - L l

__ D )

Коэффициент затухания f ( t ) = 5 ^L подбирается таким образом, чтобы динамика снижения амплитуд совпадала с результатами эксперимента [11].

В зоне IV наблюдается наибольшее давление, возникающее вследствие наложения падающей и отраженной волн:

P IV P II + P ref .

Максимальное значение давления в этой области P _max « 2,5 P_D достигается непосредственно на торце x = L .

В области V давление определяется как сумма давления в области III (область покоя) и давления в отраженной волне P ref :

Р = Р + Р

^PV ^P III + ^P ref .

Области I - V на координатной плоскости x , т описываются системой неравенств:

Область I :

x - Dt > 0 .

Область II :

x — D t <  0, x --> 0, x + C t — L\ 1 +— <  0 .

Область III :

x --< 0, x + C t - L I 1 + — l< 0.

Область IV :

x --> 0, x + — t - L I 1 + — l> 0.

Область V :

x --< 0, x + — t - L I 1 + — l> 0.

LL

Начиная с момента времени т = —I— моделирование процессов рас- пространения и отражения волн выполняется посредством наложения слабых ударных волн треугольного профиля, движущихся в противоположных направлениях со скоростями C и обладающих уменьшающейся амплитудой (рис. 2.3).

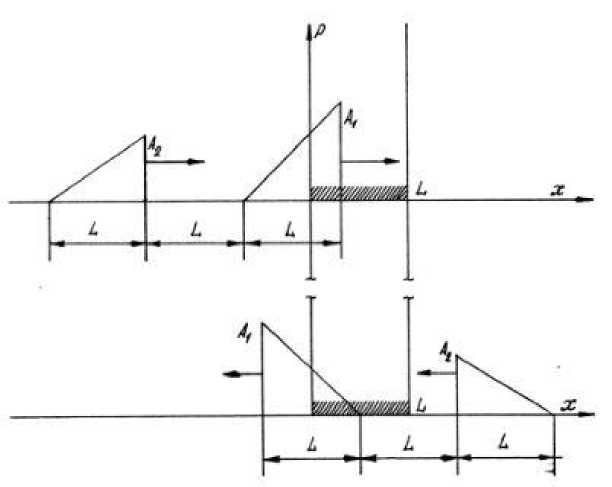
Рис. 2.3

Длины этих волн составляют 2 L, а амплитуды A k определяются следующим образом:

j -1

—

A j = A i • e ³ , j = 1,2,...

где   A 1 ~ 0,3 P D — амплитуда отраженной волны в момент времени

L L                    -— т = — + —. Коэффициент затухания e 3 также рассчитывается на основе экспериментальных данных [11]. В результате наложения данных волн формируется система из шести областей, описываемых реккурентно через каждые ^ временных интервала. Полное давление в этих областях оп ределяется добавлением давления P(т), соответствующего мгновенному сгоранию газовой смеси.

Значение давления в каждой из областей рассчитывается по следую щим формулам (рис. 2.2):

т' = т

L

L

—

—

D

C

В области 1 + 6( j — 1):

P j =

— A,- •

x + Ст' — 2( j — 1) L -------—--— + A. + P

Lj

В области 2 + 6( j — 1)

Ст'

P    2j -- + 2(2 j - 1) A j + P .

L

В области 3 + 6( j - 1)

P‘ P .

В области 4 + 6( j - 1)

j Aj'

В области 5 + 6( j - 1)

x - — т ' + 2( j - 1) L , - -------——— + A , + P .

L

5 j

В области 6 + 6( j - 1)

P 6 j = A + 1

x + —r' - 2 j'L   .

-------⁺ A j + 1

⁺ A j

x - —т' - 2( j - 1) L . - ------——— + A. + P

Lj

Данные области на плоскости x , т^г описываются системой неравенств Область 1 + 6( j - 1):

2( j - 1) L <  x + — т '< 2( j - 2) L

• - 2( j - 1) L <  x - — т ' < - 2( j - 3) L ’

Область 2 + 6( j - 1)

x + —т ' < 2( j -1)L x - —т ' <-2( j -1)L ’

Область 3 + 6( j - 1)

x + —т ' > 2( j -1)L x - —т ' >-2( j -1)L ’

Область 4 + 6( j - 1)

(2 j - 1) L <  x + — т ' <  2 jL

- (2 j - 1) L <  x - — т ' < - 2( j - 1) L ’

Область 5 + 6( j - 1)

x + —т ' < 2 jL x - —т ' <-(2 j -1) L ’

Область 6 + 6( j - 1)

x + —т ' > 2 jL x - —т ' >-(2 j -1) L '

Таким образом, в координатной плоскости x, т сформирована система областей, где давление рассчитывается по приведенным ранее формулам, аппроксимирующим экспериментальные результаты [11]. Это позволяет в каждой точке x е[0,L] определить временную зависимость давления. В качестве примера на рис. 2.4 представлена зависимость давления от вре- мени на торце x = L, полученная в рамках предложенной модели. Поскольку аналитически определить давление на внутренней поверхности камеры в данной модели затруднительно, для анализа напряженно-деформированного состояния стенок камеры применяется исключительно численный метод.

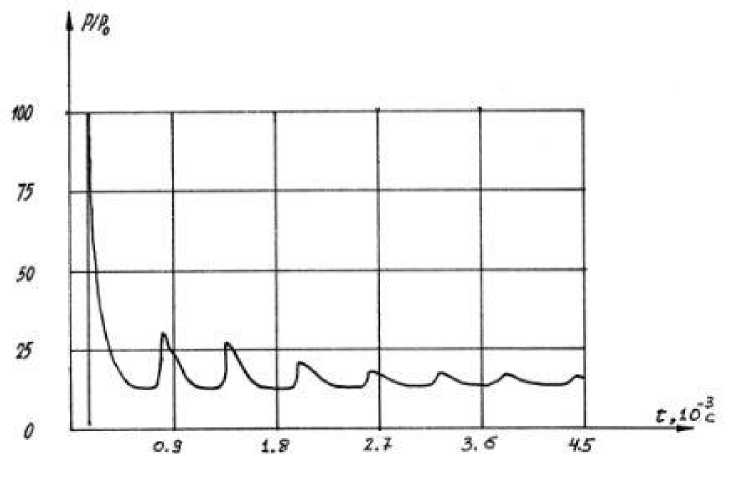
Рис. 2.4

В итоге было рассчитано давление на внутренней поверхности камер с учетом двух сценариев: мгновенной детонации и распространения детонационной волны с конечной скоростью. В последнем случае максимальное давление составило P max ~ 2,5 P D ~ 100 P 0 , тогда как при мгновенной детонации оно равнялось: P max ~ 13 P 0 .

Для расчетов использовались следующие параметры:

m = 0,343kg, Qc = 1,1-107 J-, p = 11,16k^, kgm3

^ = 0,0343 kg- , C^ = 147 —.

v 0

mol         deg

Состав газовой смеси 3 C 3 H 8 + 19 O ₂ при начальном давлении P₀ = 8 atm . Принятые размеры цилиндрической камеры: длина L = 0,15 m , внутренний радиус г ₀ = 0,075 m .

Заключение

Приведенные результаты показали, что при проектировании взрывных камер необходимо учитывать конечную скорость распространения детонационной волны, поскольку в этом случае давление может превышать расчетное давление для мгновенной детонации более чем в семь раз.