Моделирование и частотный анализ предварительно напряженных функционально-градиентных пластин с отверстиями

Модели деформирования неоднородных пластин, являющихся распространенными конструкционными элементами, весьма актуальны при решении задач, возникающих в современном строительстве (при создании перекрытий и покрытий сооружений, перегородок, заслонок, монтажных пластин и другого), в производстве военных и гражданских технических систем широкого назначения (режущих систем, мембранных датчиков, экранирующих элементов и тому подобного).

В случае однородных материалов у задач о колебаниях упругих пластин, как однослойных, так и многослойных, существуют аналитические решения. Например, в статье [1] рассмотрена задача о колебаниях круглой трехслойной пластины на упругом основании, для которой построено аналитическое решение. В случае трехслойной композитной пластины из функционально-градиентного материала в [2]

рассмотрен специальный метод расчета колебаний на основе метода Фурье–Ритца. Получены решения в виде собственных частот и собственных форм для различных типов нагружения и граничных условий.

В настоящее время новые материалы со сложной неоднородной структурой широко используются в военном и гражданском машиностроении. При этом ввиду особенностей технологического процесса изготовления таких материалов многие из них находятся в неоднородном предварительном напряженно-деформированном состоянии. В связи с этим достаточно большое количество российских и зарубежных работ посвящено моделированию неоднородных материалов, а также изучению влияния предварительных напряжений (ПН) на их прочностные характеристики. Отметим, что часто при изготовлении для улучшения механических характеристик и свойств конструкций в них специально формируют ПН. Например, в работе [3] представлены вычислительные и натурные эксперименты по изучению влияния на этапе лазерной нагартовки упругих ПН на деформированную форму образца в виде пластины из алюминиевого сплава. Разработан новый вариант метода учета влияния ПН на изгибную деформацию и образование остаточных напряжений, в котором за основу берется известный метод собственных деформаций (eigenstrain) А. Корсунского [4].

В большинстве строительных приложений при решении обратных задач о реконструкции ПН в основном анализируются процессы восстановления определенного уровня ПН или величины начального усилия, формирующего поле ПН. В статье [5] разработаны методики определения ПН в бетонных конструкциях. Авторами рассмотрена комбинация как разрушающих, так и неразрушающих методов исследования в сочетании с методом конечных элементов (МКЭ). Для иллюстрации приведены результаты для многопролетного балочного моста. При этом вычисление ПН, обусловливаемых однородными начальными усилиями, служит важным этапом в многоступенчатой экспериментальной процедуре, позволяющим добиться более высокой точности диагностирования состояния конструкции. В работе [6] описан подход к идентификации предварительного натяжения в преднапряженном бетонном мостовом настиле, базирующийся на измерении динамического отклика. Для описания настила применяется стержневая модель Эйлера–Бернулли и далее МКЭ. При этом одноосное ПН задается в виде начальных усилий в каждом конечном элементе. В постановке обратной задачи используются данные одного или нескольких измерений, полученные с помощью акселерометров или тензодатчиков.

Отметим, что вариационные и слабые постановки прямых и обратных задач играют важную роль для формулировки операторных соотношений и выбора эффективного метода численного решения. Так, во многих работах предлагаются новые численные методы решения задач линейной теории упругости, основанные на сочетании метода Галеркина и МКЭ (см., например, [7,17,18]).

В серии работ [8–14] рассмотрены вопросы моделирования и реконструкции неоднородного предварительного напряженного состояния в неоднородных тонких пластинах. В настоящей работе исследуются планарно-изгибные колебания функционально-градиентной перфорированной пластины в условиях начального напряженного состояния.

2.    Постановка задачи

Рассмотрим задачу об установившихся колебаниях тонкой упругой изотропной неоднородной пластины с плоским сечением срединной поверхности S , жестко закрепленной на части границы l_u , под действием произвольной периодически меняющейся нагрузки P_k e^{i ω t} ( ω — частота установившихся колебаний, k = 1,2,3), приложенной к части границы l _σ (Рис. 1 а ). Для общности будем считать, что все характеристики пластины: ρ — плотность, λ — параметр Ламе для плоского напряженного состояния, µ — модуль сдвига, заданы в виде зависимостей от координат x ₁, x ₂, x ₃. Пусть в пластине имеется объемное распределение ПН, заданное компонентами соответствующего тензора σ _i ⁰ _j =σ _i ⁰ _j ( x ₁, x ₂, x ₃) , где i , j = 1,2,3.

б]    1 Ре™*

в

а

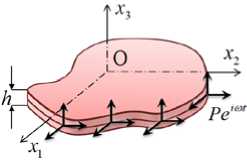
Рис. 1. Пластина произвольного сечения в режиме планарно-изгибных колебаний ( а ), перфорированная прямоугольная пластина ( б ), пластина при наличии функционально-градиентного перехода ( в )

Нелинейные свойства упругих тел проявляются в том, что после предварительного деформирования распространение малых возмущений в них зависит не только от свойств материалов, но и от величины начальной деформации. В качестве основной возьмем линеаризованную постановку задачи о колебаниях предварительно напряженного тела без явного учета начальной деформации. Предположим, что начальное деформированное состояние определяется в рамках геометрически линейной теории, вследствие чего градиентами начальных перемещений можно пренебречь [16]. Такой вариант упрощения задачи для предварительно напряженного тела распространен и в самом общем случае. Подробный обзор наиболее используемых линеаризованных моделей предварительно напряженных тел, включая и применяемую в настоящей работе, приведен в статье [13].

Таким образом, задача об установившихся колебаниях анизотропного тела с учетом ПН имеет следующую постановку:

( C ijki u k , i + u i , m ^ mj) ^,j +Pto¹ U = ⁰ ,                                                ⁽¹⁾

u i ¹ S u = 0,         ( C ijki u k , l + u i , m ^ n j\S = P i .                                      ⁽²⁾

Здесь считается, что поверхность тела в текущей конфигурации представима в виде: S = S u и S _т, причем тело жестко защемлено на части S u и нагружено периодически меняющейся нагрузкой на части S _а . Компоненты C_ijkl образуют тензор упругих модулей, u i — компоненты вектора малых перемещений.

На основе общей постановки (1), (2) сформулируем задачу об установившихся связанных планарно-изгибных колебаниях описанной выше пластины. Согласно теории пластин Тимошенко [15], соответствующие гипотезы (с добавлением планарной составляющей перемещений) будут иметь вид:

U 1 = 0 , x ₃ +Z i , u ₂ = 0₂ x ₃ + Z ₂, и з = w, (3)

где 0_а = 0_а ( x в) — углы поворота нормали n относительно осей x _а , Z_a = Z_a ( Х в ) — перемещения в срединной плоскости пластины, w = w ( Х в ) — прогиб пластины (здесь а, р = 1,2). На основании вариационного принципа для предварительно напряженного упругого тела в рамках линеаризованной модели (1), (2) [12] и с учетом гипотез деформирования (3) постановка краевой задачи формулируется в виде:

Q ав , в- S a+®²( ^P1 Za+ Р 2 0а ) = 0,       R „щ, + to 2 (Р^ + Р 1 0а ) = 0,       Т„„ a + P^ W = 0,       (4)

Wl u = 0      Z a l l u = ⁰ ,      ⁰     = ⁰ ,

Qав neh„ = 0,    Rав ПвЬ„ = Pa ,    Tana 1I,= P3, где обозначено:

Qaв =5ав (Л20 m, m     m, m ) + M^ +0^ ) + M^ + Z^ ) + ^"m в0а, m +^m вZa, m +^в3 0.

Rав ^ . (Л10m,m +Л0Zm,m ) + М1(0а,в +0в,а ) + M°(Za,в + Zв,a ) + ^в0а,m + 2^вZa,m +^0.

Sа = M0 (W ,а +0а ) + 2^ 30а, m + 2m зZa, m + ^а ,       Та = M0 (W,а + 0а ) + 2аmW, m ,

G p = j gx^dx 3 ,       G p = { ^Л p , ^M p , ^p p , ² ав } ,       g = { x,ц,P,^ав }       (а,в, m = 1,2, p = 0,1,2),

- h /2

Pp — интегральные характеристики плотности (p = 0,1,2), m — индекс, по которому осуществляется суммирование, Ра — компоненты вектора нагрузки в плоскости S пластины, P3 — интенсивность изгибной нагрузки [14]. Введенные функции Gp представляют собой обобщение закона для интегральных характеристик Лp ,Mp,Рp,2ав, выражаемых через соответствующие параметры X, ц, р, ^в, например:

h /2

h /2

у^{2 2} 12

= j ^с 1°2 x 32 dx 3 , Р 1 = j P x 3 dx 3

-

h /2

-

h /2

Отметим, что здесь рассматриваются совместные планарно-изгибные колебания пластины, и задача в такой постановке может быть сведена к раздельным задачам о планарных и изгибных колебаниях, но только при выполнении дополнительных условий симметрии, описанных в работе [14]. Для цельной пластины с постоянными характеристиками и однородным полем ПН (по всем координатам) эти условия выполняются автоматически, и, следовательно, задачу для пластины можно решать по отдельности для каждого из режимов колебаний.

Обозначим буквами 0_a, Z_a, W пробные функции, удовлетворяющие тем же главным условиям, что и, соответственно, функции 9_a, Z_a, w :

0.1 , . = 0,      ^z . I , . = 0,      Wk = 0.                                    (6)

Тогда, согласно гипотезам (3) и граничным условиям (6), слабая постановка сформулированной задачи примет вид:

( pz + PW ) di - f I Qa в®™ + R_a Za + , _a 0, + TW ,« -

J \ a a 3   / J (-ap a , p ap a , p a a a "a

• I ,                                S

  -to² [P 2 0a0a + P ( 9aZa + Z^ a ) + P ( ZaZa + WW ) ] } dS = 0.                     (7)

На основе слабой постановки (7) исследуем частную задачу о колебаниях неоднородной пластины с круговыми отверстиями (см. Рис. 1 б ). Пластина выполнена из функционально-градиентного материала, свойства которого непрерывно меняются по поперечной координате в соответствии с обобщающим законом неоднородности F для материальных параметров пластины X, ц, р :

n

F ( х з ) = ( F - F 2 )Z l +0Z h 1 + _F2 . V h /

Здесь: F 1 и F ₂ — физико-механические характеристики материала на поверхностях пластины х 3 = ± h / 2 .

Уравнения движения, исходя из (4), (5), принимают вид:

Q 11,1 + Q 12,2 - S i 'И(1Х + P 2 9 1 ) = 0,

Q 21,1 + Q 22,2 - S 2 + ®Ш 2 + P 2 9 2 ) = 0,

41 + R 12,2 + ® 2 (P 0 Z 1 + P 1 9 1 ) = 0,                                           (9)

R 21,1 + R 22,2 + ®²(P 0 ? 2 + P i 9 2 ) = 0,

T 1 + T 2 2 + P a ®² W = 0.

Соответствующие граничные условия записываются так:

w k = 0,      9 1 l . = 0,       9 2 1 . = 0,       Z i l i . = 0,       Z 2 b . = 0,

( ^Q 11 n 1 ⁺ Q 12 n 2 ) 1 1 , = ⁰ ,         ( ^Q 21 n 1 ^{+ Q} 22 n 2 ) 1 1 , = ⁰ ,                                           (10)

( R_nn + R 12 n 2 ) b , = P 1 ,      ( R 21 n + R 22 n 2 ) b . = P 2 ,      ( TП 1 + T 2 n 2 ) b . = P 3 .

Условимся, что в рамках плоского напряженного состояния поле ПН в пластине не зависит от поперечной координаты, то есть ^р = °ap( X i , x 2 ), где a,P = 1,2 . В этом случае входящие в (7) слагаемые могут быть представлены в виде:

Q 11 = Л 2 ( 9 1,1 + 9 2,2 ) + Л 1 ( Z 1,1 + Z 2,2 ) + 2M 2 9 1,1 + 2M 1 Z 1,1 + 2 21 9 1,1 + 2 222 0 1,2 + 2 J1 Z 1,1 + S j ₂Z 1,2 ,

^Q 22 = ^Л 2 ^{( 9} 1,1 ^{+ 9} 2,2 ) ^{+ Л} 1 ^{( Z} 1,1 ^{+ Z} 2,2 ) ^{+ 2M}2 ⁹ 2,2 ^{+ 2M}1 ^Z 2,2 ^{+ 2} 12 ⁹ 2,1 ^{+ 2} 22 ⁹ 2,2 ^{+ 2} 12 ^Z 2,1 ^{+ 2} 22 ^Z 2,2

^Q 12 = ^M2^{( 9} 1,2 ⁺⁹ 2,1 ) ^{+ M}1^{( Z} 1,2 ^+Z 2,1 ) ^{+ 2} 12 ⁹ 1,1 ⁺² 22 ⁹ 1,2 ⁺² 12 ^Z 1,1 ⁺² 22 ^Z 1,2 ,

^Q 21 = ^M2 ^{( 9} 1,2 ^{+ 9} 2,1 ) ^{+ M}1 ^{( Z} 1,2 ^{+ Z} 2,1 ) ^{+ 2} 11 ⁹ 2,1 ^{+ 2} 12 ⁹ 2,2 ^{+ 2} 11 ^Z 2,1 ^{+ 2} 12 ^Z 2,2 ,

R 11 = Л 1 ( 9 1,1 + 9 2,2 ) + Л 0 ( Z 1,1 + Z 2,2 ) + 2M 1 9 1,1 + 2M 0 Z 1,1 + 2 11 9 1,1 + ^ 12 6 1,2 + 2 01 Z 1,1 + S 0 ₂Z 1, ₂, ^R 22 =^Л 1 ( ⁹ 1,1 ⁺⁹ 2,2 ) ^{+ Л} 0 ( ^Z 1,1 ^+Z 2,2 ) ^{+ 2} M 1 ⁹ 2,2 ^{+ 2} M 0 ^Z 2,2 ^{+ 2} 12 ⁹ 2,1 ⁺² 22 ⁹ 2,2 ^{+ 2} 12 ^Z 2,1 ⁺² 22 ^Z 2,2 , R 12 = M 1^{( 9} 1,2 ⁺⁹ 2,1 ) ^{+ M}0^{( Z} 1,2 ^+Z 2,1 ) ^{+ 2} 12 ⁹ 1,1 ^{+ 2} 22 ⁹ 1,2 ⁺² 12 ^Z 1,1 ⁺² 22 ^Z 1,2 ,

R 2i - M i (0 i,2 +6 2,1 ) + M o (C i,2 ^+Z 2,1 ) + ^ 11 ^ 2,1 +^ 12 ^ 2,2 ⁺ ^ 1l C 2,1 +^ 12 ^ 2,2 ,

5 - M o ( w , 1 +6 1 ) 1 ,       S 2 - M o ( w , 2 +6 2 ),

T - M o ( w , 1 +6 1 ) -2 w , 1 + 2 w , 2 ,        T 2 - M o ( w , 2 +6 2 ) ■ 2 w , 1 ■ 2 w , 2 .

Осредненные характеристики для ПН с учетом принятых гипотез станут следующими:

h /2                      1            P 1 \P +1   /   7 \ P +1 't

V P — f —0 „P _   ¹ „0 I h I I h I

2«P - J GaPx3 dx3 -      1 a«P I ? I I ? I ,

• -h/2             p + 1 VV2 J V 2 J J

  
  

h /2                                                h /2                                              h /2                       1

• 2aP - J CTaPdx3 - hCTaP ,       2aP - J CTaPx3 dx3 - 0,       2aP - J CTaPx3 dx3 - h CTaP .

  - h /2                                       - h /2                                     - h /2                ¹²

Осредненные характеристики материала с учетом того, что он является функционально-градиентным (см. (8)) при n - 2 примут вид:

h /2

h /2 I

F p - J Fx ^ dx 3 - J ( F - F 2 )

2 x ₃ + 0.5 h I

- h /2

-

-h /2 V

h

I

+ F 2 x 3 p dx 3 , J

h /2

F 0 - J Fdx 3 - - ( F 1 + 2 F 2 ) h ,

- h /2           ³

h /2                  1

^F1 ^- J ^Fx 3 dx 3 ^- —( ^F1 - F 2 ) ^{h 2},

- h /2             12

h /2

F ₂ - J Fx ₃ ² dx ₃ -

- h /2

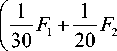
h 3 .

Таким образом, задача об установившихся планарно-изгибных колебаниях пластины в условиях плоского напряженного состояния (11) и при осредненных интегральных характеристиках (12), (13) сводится к краевой задаче (9), (10). Далее на ее основе исследовано влияние неоднородного предварительного напряженного состояния перфорированной прямоугольной пластины, изображенной на рисунке 1 б , на ее амплитудно-частотные характеристики и резонансные частоты.

3. Вычислительные эксперименты

Задача решалась численно с помощью МКЭ для различных функционально-градиентных законов, моделирующих металлокерамики и металлические сплавы. Для увеличения точности расчетов в зонах круговых отверстий использовано локальное сгущение конечно-элементной сетки. Проведен анализ влияния различных типов неоднородного предварительного напряженного состояния пластины на ее динамические (амплитудно-частотные) характеристики и собственные частоты. Важно, что предложенная модель позволяет задавать в пластине предварительное состояние произвольно: как в виде аналитических зависимостей, так и численно. Далее описывается численный эксперимент, когда в качестве ПН выступают поля напряжений, образованные в пластине в результате приложения к части ее границы некоторой начальной механической статической нагрузки. Для отыскания в рассматриваемой пластине такого поля дополнительно решалась соответствующая задача статики.

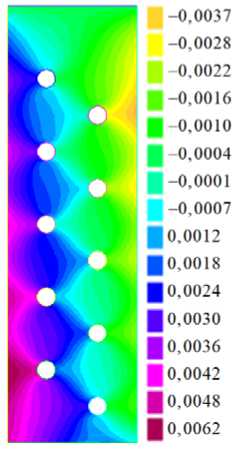
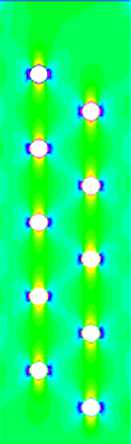
На рисунках 2 и 3 приведены поля предварительных перемещений u 1 ⁰, и ⁰ и ПН ст ^ , а ° ₂, а 2 ₂, образующиеся в соответствующей модельной (статической) задаче, в которой пластина подвергается начальному растяжению в направлении оси x 1 за счет приложения механической нагрузки р 1 -150 МПа. При этом использованы следующие параметры: l -1,0 м (размер пластины вдоль оси x 1 ); b - 0,3 м (размер пластины вдоль оси x ₂); h - 0,05 м; материалы фаз — медь (фаза F 1 ) и вольфрам (фаза F 2 ), у которых E 1 -110 ГПа, V 1 - 0,35, р 1 - 8900 кг/м³, E ₂ - 350 ГПа, v₂ - 0,29, р₂ -19300 кг/м³. В пластине имеется 10 сквозных отверстий диаметром 0,021 м. Все результаты вычислений приведены для пластины, расположенной так, как показано на рисунке 2 а. На шкалах рисунков 2 и 3 перемещения равны и ⁰ х 0,1 м, напряжения — ст⁰ х 0,1 МПа.

Равновесие пластины во вспомогательной задаче статики описывается уравнениями:

^R 11,1 ⁺ R 12,2   ⁰ , R 21,1 ⁺ R 22,2   ⁰ ,

а

б

0,0021

0,0064 1 0.0107 1 0.0150

| 0,0192 0,0235 0,0278 1 0,0321 | 0.0364 ■ 0.0407 1 0.0449 1 0,0492 | 0,0535 I 0,0578 | 0.0685

в

Рис. 2. Конечно-элементное разбиение пластины в плоском случае ( а ), картины полей начальных перемещений u ₁⁰ ( б) и u ₂ ⁰ (в )

а

-176.728

178,163

|533,054 1887,945 11242,84 11597,73

1952,62

12307,51 12662,40 13017,29 13372,18 13727,07 14081,96 14436.85 15324,08

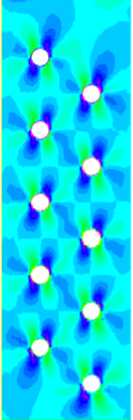
б -1209,19

1-1036.11

1-863.024 1 -689,942 1-516,859

| -343,777 1-170,695 1 2,3871 1175.469 1348,551 1521,634 1694.716 1867,798 11040,88 11473,59

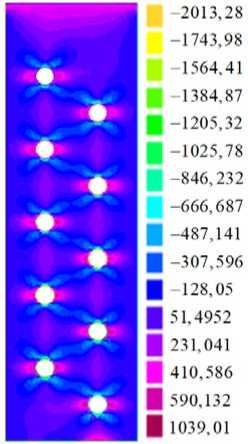
в

Рис. 3. Поля предварительных напряжений: о , ⁰ .

⁽ а); 0 02 ⁽ б ); о ^2 ⁽ в )

где введенные выше функции выглядят так:

R 11 = А_о ( Z_ц +Z₂ , ₂ ) + 2M₀Z у ,        R 12 = R 21 = M o (Z 1,2 + Z 2,1 ),

R 22 = ^Л 0 ( ^Z 1,1 ^{+ Z} 2,2 ) ^{+ 2M}0 ^Z 2,2 ^.

Слабая постановка при этом трансформируется к виду:

0 = J P ^ Z i dl — J ( R _nZ_H + R 12 (Z i 2 + Z 21 ) + R 22 Z 22 ) dS . l „                 S

Функции решения отсюда — Z1 , Z₂, R 11 , R ₁₂, R ₂₂, могут быть использованы в качестве полей предварительных перемещений и напряжений — u 1 ⁰, и ⁰ и 0 ° , о^, о 22 , соответственно, при решении задач в рамках линеаризованных постановок для предварительно напряженных тел. В данном случае, в силу выбранной модели, в дальнейшем будем учитывать в явном виде только компоненты ПН.

На рисунках 4 и 5 приведены поля прогиба, углов поворота нормали и планарных перемещений, рассчитанных в статическом случае (при ω=0) для перфорированной пластины с учетом предварительного нагружения в рамках слабой постановки (15). Величина изгибной нагрузки при этом равнялась p3 = -10 МПа и была приложена на границе x1 = l. На шкалах рисунков 4 и 5 прогибы равны w × 0,1 м.

-3,3454 а

-3.0318

В -2,8226 | -2.6135 g-2,4044 g -2,1952 |-1,9861 |-1,7779 g-1,5678 g-1,3587 g 1.1496 g-0,9404 g -0,7313 g-0,5222 g 0,313 go, 2097

-0,003 б

0,0018

0,0045 g 0.0076 ■ 0.0106 g0.0136

0.0167

0.0197 g 0.0227 g 0,0258 go, 0288 g 0,0318 g 0,0349 g 0,0379 g 0,0410 10,0486

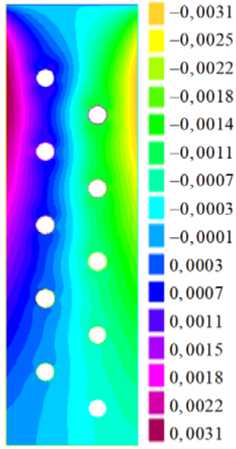
в

Рис. 4. Поля прогиба пластины w (а) и углов поворота нормалей: θ ₁ ( б ); θ ₂ ( в )

-0.0011

0.0005

0,0016

0,0027 g 0,0039

| 0,0050

0.0061

0,0072 g 0.0084 g 0,0095 go.0106 go,0117 go,0128 g 0,0139 g0.0151 10.0179

а

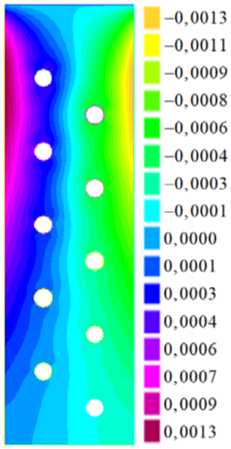
б

Рис. 5. Поля планарных перемещений пластины: ζ ₁ ( а ); ζ ₂ ( б )

На рисунке 6 представлены амплитудно-частотные характеристики пластины, вычисленные в точке ( l , 0) без учета и с учетом поля ПН; при этом значения амплитуд колебаний равны w × 0,1 м, а значения частот колебаний f приведены в Гц. По построенным кривым видно, что выбранное неоднородное поле ПН, образовавшееся в результате приложения механической нагрузки, вносит существенный вклад в их изменение и сдвиг резонансных частот. Аналогичный анализ влияния различных типов однородного и неоднородного предварительно напряженного состояния на акустические характеристики пластин при планарных колебаниях, а также при изгибных колебаниях в рамках классической модели Кирхгофа был проведен в работах [12, 13].

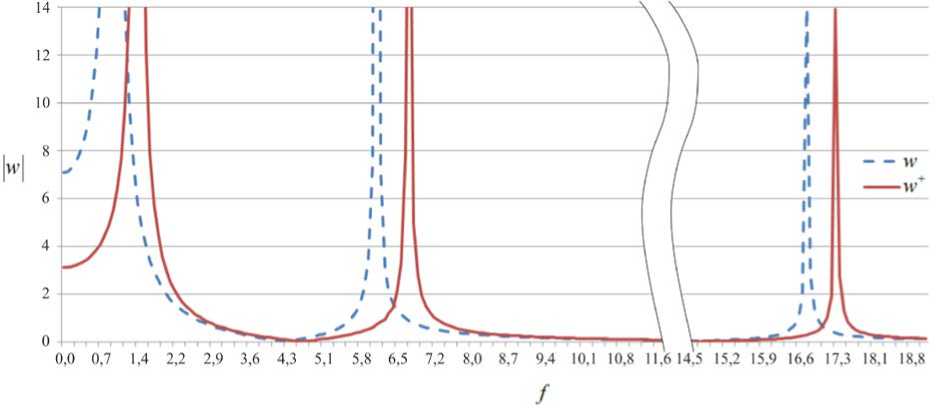
Рис. 6. Амплитудно-частотные характеристики пластины в точке ( l ,0) без учета ( w, штриховая линия) и с учетом поля предварительных напряжений ( w+, сплошная линия)

4. Выводы

Предложенная для описания колебаний предварительно напряженной пластины модель позволяет задавать произвольную геометрию сечения пластины (в том числе с отверстиями), учитывать неоднородность материала (в плоскости пластины и по толщине), а также предварительное напряженное состояние в пластине как в виде аналитических зависимостей, так и численно.

Полученные результаты анализа влияния неоднородного предварительного напряженно-деформированного состояния на амплитудно-частотные характеристики и резонансные частоты могут быть положены в основу изучения обратных задач, когда требуется реконструкция параметров ПН на базе акустического зондирования. Например, для рассмотренной перфорированной пластины на основе данных акустического зондирования можно поставить задачу восстановления параметра ПН.

При зондировании нагрузкой, действующей в плоскости пластины, согласно постановке задачи для планарных колебаний пластины,

R 11,1 ⁺ R 12,2 ⁺ ® ^P0 ^Z 1   ⁰ ,        R 21,1 ⁺ R 22,2 ⁺ ® ^P0 ^Z 2   ⁰ ,

где функции имеют вид:

R 11 = Л о ( Z 1,1 + Z 2,2 ) + 2M o Z 1,1 + ^ 01 Z 1,1 + SZy ,       R 12 = M o (Z_y + Z 2,1 ) + ^ 02 ^ 1,1 + ^ 22 ^ 1,2 ,

^R 22 = ^Л 0 ^{( Z} 1,1 ^{+ Z} 2,2 ^{) + 2M}0 ^Z 2,2 ⁺ ^ 12 ^Z 2,1 ⁺ ^ 22 ^Z 2,2 ’

^R 21 = ^M0^{( Z} 1,2 ^{+ Z} 2,1 ) ⁺ ^ 11 ^Z 2,1 ^{+ S} 12 ^Z 2,2^.

Слабая постановка будет выглядеть при этом следующим образом:

0 = J ( P 1 Z 1 + P ₂ Z ₂ ) dl - J ( R ₁₁Z₁ , ₁ + R ₁₂Z 1, ₂ + R ₂₁Z₂ ,1 + R ₂₂Z₂ , ₂ -to²P₀(Z₁Z₁ + Z₂Z₂) ) dS .

l „

S

Рассмотрим модельную ситуацию, когда известна априорная информация о виде начальной механической нагрузки, вызвавшей предварительное состояние пластины. Так как компоненты тензора ПН линейно зависят от начальной нагрузки, то можно записать: S^ = ph 6, где p — интенсивность начальной нагрузки, приложенной к части свободной границы пластины, 6 ^_р = ст Оз / р — характерное поле ПН с известной структурой. С учетом этого представления в статическом случае (при ® = 0) на основе уравнений движения (16) получается формула:

P = -

^{1 (Л} 0 ^{+ 2M}0 ) ^Z 1,11 ^{+ (Л} 0 ⁺ M o ) ^Z 2,12 ^{+ M}0 ^Z 1,22

h   [6 01 Z 1,1 +6 02 Z 1,2 ]₄ +[6 02 Z 1,1 +6 22 Z 1,2 ] , ₂

,

которая позволяет определять параметр p исходя из набора данных измерений планарных компонент смещения ζ₁, ζ₂ в точках пластины. Затем по этим значениям можно построить функции компонент перемещений, например, с помощью сплайн-интерполяции и далее выразить первые и вторые производные перемещений, входящие в формулу (17). Полученная формула дает возможность проводить вычислительные эксперименты по реконструкции параметра ПН p для различных видов начальной механической нагрузки.

Исследование выполнено при финансовой поддержке Российского научного фонда (грант 18-71-10045).