Моделирование и численный расчет поршневого вытеснения нефти для двоякопериодических систем разработки месторождений

Нефтедобыча представляет собой сложный процесс, требующий самых современных технологий. Существует множество способов извлечения нефти из пласта. Так, под первичными методами подразумеваются те, с помощью применения которых нефть самотеком поступает в ствол скважины под воздействием пластового давления. Среди вторичных методов, или методов улучшения нефтеотдачи (Improved Oil Recovery — IOR), широкое распространение получил метод заводнения. Заводнение — одна из старейших технологий в нефтяном промысле, за многие десятилетия доказавшая свою эффективность на месторождениях различных нефтедобывающих стран [1, 2]. Основная цель заводнения заключается в поддержании пластового давления, неизбежно падающего в процессе первичной разработки залежи. Для восстановления пластового давления в горную породу через специально пробуренные нагнетательные

(или ранее отключенные добывающие) скважины закачивается вытесняющий агент (как правило, вода), в результате чего пластовое давление повышается до необходимого уровня. Заводнение и в наши дни широко распространено в нефтяном промысле. В связи с этим актуальными остаются задачи повышения эффективности данной технологии, в том числе и на стадии ее проектирования. При проектировании весьма важной является оценка потенциальной эффективности заводнения при различных способах взаимного расположения разнопрофильных скважин — одного из ключевых аспектов технологии.

Моделирование процесса заводнения, анализ его качественных и количественных характеристик при различных схемах расстановки скважин — цель настоящего исследования, объект исследования — текущий фронт вытеснения, видоизменяющийся в процессе нагнетания воды в пласт и вытеснения ею нефти. В качестве базовой используется модель поршневого вытеснения нефти водой [3]. Эта модель, в отличие от модели «разноцветных» жидкостей [4], допускает различие в физических свойствах (в величинах плотности и вязкости) вытесняемой и вытесняющей жидкостей. Особенности процесса заводнения для двоякопериодических систем разработки месторождений в рамках модели «разноцветных» жидкостей рассмотрены в работе [5].

Задача продвижения фронта вытеснения при различных физических свойствах нефти и воды имеет более чем полувековую историю. Впервые поставленная в середине XX века М. Маскетом [6], в дальнейшем она вызывала интерес многих исследователей. Можно отметить метод недеформируемых трубок тока, описанный в общем виде И.А. Чарным [7]. В основе идеи автора лежало допущение о совпадении линий тока при фильтрации двух- и одножидкостной систем в некоторой области при неизменных граничных условиях. Иной подход, основанный на теории потенциалов, предложен В.Л. Даниловым [8], где исходная задача мониторинга фронта вытеснения во времени сведена к нелинейному интегро-дифференциальному уравнению. Метод Данилова был распространен Р.Т. Фазлыевым [9] на случай площадного заводнения; автор построил и численно решил интегро-дифференциальное уравнение для пятиточечной схемы заводнения. В обзорной работе М.Х. Хайруллина [10] рассмотрены работы казанской научной школы в области подземной гидромеханики, в том числе и в области моделирования процессов заводнения.

Настоящая работа обобщает ранее полученные результаты на случай поршневого вытеснения. Согласно модели «разноцветных жидкостей» вектор скорости остается непрерывным на протяжении всего процесса заводнения. В случае же поршневого вытеснения — при совместном течении нефти и воды, указанная непрерывность нарушается: различие физических свойств жидкостей приводит к разрыву касательной компоненты вектора скорости фильтрации при сохранении непрерывности нормальной компоненты и значения давления на фронте вытеснения.

2.    Математическая модель продвижения фронта вытеснения Рис. 1. Графическое представление системы разработки месторождения при пятиточечной обращенной схеме заводнения; границы повторяющихся элементов очерчены пунктиром; добывающие скважины выделены черными точками, нагнетательные - треугольниками

Рассмотрим плоское фильтрационное течение жидкости с вязкостью ц в бесконечном горизонтальном пласте толщиной h , имеющем постоянные величины проницаемости к и пористости m . Моделируемый пласт покроем двоякопериодической системой добывающих и нагнетательных скважин (Рис. 1).

Предполагается, что скважины рассматриваются как вертикальные точечные источники / стоки и являются совершенными по степени и характеру вскрытия [1-3]. Для квазистационарного режима фильтрации функция давления в пласте p ( x , у , t )

удовлетворяет уравнению пьезопроводности, а компоненты вектора скорости V_x ( x , у , t )

и V y ( x , y , t ) вычисляются по закону фильтрации Дарси [1, 3]:

• д p     Г д ² p д ² p )

= х +

д t     (д x ²    д у ² ) ’

к д p         к д p

=---,     V y =---.

ц дx         ц ду

Первое уравнение в (1), где х — коэффициент пьезопроводности, является основным дифференциальным уравнением упругого режима фильтрации жидкости в пласте.

Двоякопериодическую сетку добывающих и нагнетательных скважин можно представить как достаточно большое (в математической модели — бесконечно большое) число повторений конечного числа скважин в двух направлениях. Такие повторения можно описать с помощью двоякопериодической решетки (Рис. 2; z ₀ — центр нагнетательной скважины).

Двоякопериодическая решетка определяется двумя неколлинеарными векторами на плоскости ( x , у ) (двумя комплексными периодами to 1 и ю ₂ — на комплексной плоскости z = x + iy ). Для простоты будем считать, что вектор ® j направлен вдоль оси x , то есть комплексный

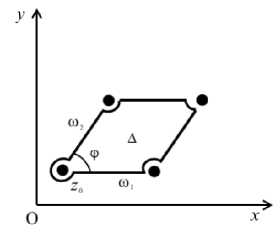
Рис. 2. Двоякопериодическая решетка и ее основные элементы

период ®j является вещественным числом. Все множество узлов решетки на комплексной плоскости формируется как to = ito1 + jto2 (i, j = 0, ± 1, ±2,...), величины X и ф (to2/to1 = Xexp(iф)) характеризуют размеры и форму решетки, а д= Тш(ю1ю2) соответствует площади параллелограмма решетки (здесь и далее надчерком обозначена сопряженная величина).

В работах [11, 12] представлено решение квазистационарной задачи (1) при разработке месторождения двоякопериодической системой только добывающих скважин, размещенных в узлах решетки. Распределение поля давлений и скоростей в этих работах выражено через сигма- и дзета-функции Вейерштрасса и имело вид:

Q ц                 Z ² I ^z

p ^{( x} , У ) = P w +      I ^Re I In o ^{( z} ) + ^a—l-P     ^- In r w

2 n kh V V            2 )    2 _y

Vx ⁽ x , У ) ^{- iV}y ⁽ x , У ) = V ^{( z} , z ) = - ^Q ( ^{Z ( z} ) ^{+ a z} -P ^z ) , 2 n h

где pw — давление на контуре добывающей скважины; rw и дзета-функции     Вейерштрасса,     то     есть

радиус скважины; g ( z ) и Z ( z ) — сигма-

со ln g(z) = In z + ^ ' i, j=-о

ln

z

to

z

z

to

to 2to2

о

• 1    x1 J 1       1 z I

Z ( z ) = —+ >  ' I----+—+—2" l ; символ «'»после знаков двойной суммы означает отсутствие слагаемого z i , j =-о V ^{z -to to to} )

при i = j = 0; числовые параметры Р = л/ д и a = (pto1 - 2Z(to1/2))/to1 обеспечивают двоякую периодичность функций Z(z) и ln g(z); Q — мощность (дебит) добывающей скважины.

В работе [13] решение (2) обобщено на случай двоякопериодической группы (кластера) из n добывающих скважин; распределение поля скоростей записывалось как

V ^{( z} , ^z ) = ^- Е Uh ( ^{z ( z - z}k ) ^{+a ( z - z}k ) ^{- e (} z ^- z k ) ) ,

где z_k — расположение k -й добывающей скважины в параллелограмме периодов, а Q_k — мощность (дебит) этой скважины.

При наличии в параллелограмме периодов как добывающих, так и нагнетательных скважин в рамках модели «разноцветных» жидкостей представление (3) сохраняется. Только весь кластер из n скважин разбивается в этом случае на сумму из n ₁ добывающих скважин, для которых мощность скважин Q_k положительна, и n ₂ нагнетательных скважин, для которых мощность скважин Q_k отрицательна. В такой постановке задача нахождения поля скоростей и определения текущего положения фронта вытеснения в рамках модели «разноцветных» жидкостей рассмотрена в работе [5].

Как уже было отмечено, при описании вытеснения нефти водой поршневой моделью задача продвижения фронта вытеснения усложняется за счет нарушения непрерывности вектора скорости и преломления линий тока на фронте. Физические различия в вязкости вытесняемой и вытесняющей жидкостей обуславливают разрыв касательной компоненты V t вектора скорости фильтрации; при этом нормальная компонента V_n , а также значения давления p на фронте остаются непрерывными. Совокупность перечисленных условий на фронте вытеснения можно представить как следующую систему [3, 6, 9] (индекс ( о ) относится к частицам нефти, а индекс ( w ) — к частицам воды):

у ⁽ o >ц   = J7⁽ w >u

V t   ^ ( o )      V t    ^ ( w ) ,

⁽ o ) _ у ⁽ w w)

V n V n , p ⁽ o ) = p ⁽ w ⁾.

Разрывную на фронте, но двоякопериодическую на комплексной плоскости функцию V ( z , z ) будем искать в виде:

V ( z , z ) = Ф ( z , z ) + -¹- (6z( t- z ) y ( t ) d t , 2 n i L

где Ф ( z , z ) определяется выражением (3), характеризующим непрерывное распределение поля скоростей

по «разноцветной» модели. Второе слагаемое в

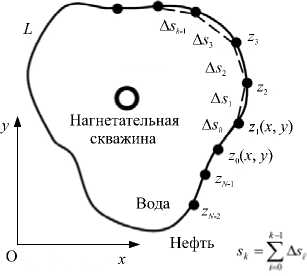
Рис. 3. Схема параметризации фронта вытеснения (линия L ) и ее дискретного разбиения точками z_k ( к = 1,... N ) ; ввиду замкнутости контура L следует, что z о = zn

правой части формулы (5) представляет собой сингулярный интеграл по линии фронта вытеснения L с ядром типа Коши, заключенным в дзета-функции Вейерштрасса     Z ( t — z ).

Представление в виде (5) впервые использовано Койтером в его работе [14], посвященной двоякопериодическим задачам теории упругости. Автор сводит исходную краевую задачу к сингулярному интегральному уравнению, включив в него двоякопериодические функции, построенные на базе дзета-функции Z ( z ).

Воспользуемся введенным представлением (5) для отыскания неизвестной на L функции у ( т ). Задавая естественную параметризацию контура L , основанную на длине дуги 5 (Рис. 3), и применяя к (5) формулы Сохоцкого-Племеля [15], получим следующую систему уравнений:

^V * w ^{)( z ( 5} )) = ^{Ф ( z ( 5} )) ^{+ 1}— f ^Z ( ^{z (} ° ) — ^{z ( 5 )} > У ( ^{z (} ° ) ) dd G + ^^ z y ⁵ )), 2 n i L                        d °        2

V⁽o ^{)( z ( 5} )) = ^{ф ( z ( 5} )) ⁺ 1— f^z ( ^{z (} ° ) — ^{z ( 5} ) ) y ( ^{z (} ° ) ) dzd ° — ^{y (} z^⁵ )) . 2 n i L                       d °        2

Для неизвестной на L функции у ( 5 ), а также для комплексной скорости V ( 5 ) перемещения точек линии z ( 5 ) из соотношений (6) следуют их представления через комплексные функции скоростей V⁽ ’ ( 5 ) и V⁽o ) ( 5 ):

Y ( 5 ) = V⁽ w ) ( 5 ) — V⁽ o ) ( 5 ), V ( 5 ) = ( V⁽ w ) ( 5 ) + V⁽ o ) ( 5 ) ) /2.

Принимая во внимание условия (4) на границе фронта вытеснения, а также представление комплексной функции скорости V ⁽ ) ( 5 ) через ее касательную и нормальную компоненты V t⁽w ) ( 5 ), V nw ) ( 5 ) в виде V⁽ ) ( 5 ) = [V t⁽w ) ( 5 ) + iV nw ) ( 5 )] e~i ^a , получим следующие выражения для функций у ( 5 ) и V ( 5 ) :

у ( 5 ) = 1 1 -^ ( w ^ I V^w ) ( 5 ) e -i ^a , I    ^ ( o ) J

V ( 5 ) =

)

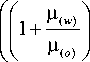
V t ⁽ w ) ( 5 ) + 2 iV n w ) ( 5 ) J

e i ¹¹

/2,

где a — угол между касательной к линии L и осью x .

Обозначим отношение вязкостей через коэффициент мобильности: к = ц(w)/ц(o) , а касательную и нормальную компоненты вектора скорости воды, соответственно, как T(5) = Vt(w) (5) и N (5) = V,( w)(5). Известно, что угол a между касательной к L и осью x, проведенной через некоторую точку z(5), связан с производной dz(ds по параметру s в этой точке соотношением e'“ = dz/ds. В результате из соотношений (7) получим сингулярное интегральное уравнение в комплексной форме для неизвестных функций T(s) и N(s) :

T ( s ) + 'N ( s ) =

- — —

Ф ( s ) '

2 п '

J Z ( z ( о ) - z ( s ) ) T ( о ) d ° dz .

3. Алгоритм построения решения задачи продвижения фронта вытеснения

Интегральное уравнение (8) для касательной T ( s ) и нормальной N ( s ) компонент вектора скорости воды на фронте вытеснения необходимо дополнить дифференциальным уравнением, определяющим эволюцию этой границы во времени. Данное уравнение можно записать в следующем виде [5, 9]:

d z ( s , t ) —. .

m \ ’ = V ( s , t ),                                                 (9)

о t где z(s,0) = z0 + rwe'6 — начальное условие (z0 — центр нагнетательной скважины радиуса rw, через которую в пласт закачивается вода). Функция V(s, t) равняется скорости перемещения точки z, расположение которой на фронте обуславливается текущим значением параметра s этой границы в момент времени t. Условие для z(s,0) в (9) указывает на положение точки на траектории ее движения в момент начала заводнения. Направление траектории определяется начальным значением угла 6 соответствующего трассера на контуре нагнетательной скважины. Фактически по мере развития фронта вытеснения параметр s с течением времени становится функцией как 6 , так и t .

С учетом представления (7) для функции V ( s , t ) в точках фронта вытеснения уравнение (9) можно переписать в виде:

d z ( s , t ) Г ( 1 + ^— ) m -----= -----

d t

T ( s , t ) + IN ( s , t ) e ‘ “ ,

(-0)

где функции T ( s , t ) и N ( s , t ) для данного момента времени t находятся из решения сингулярного интегрального уравнения (8).

Рассмотрим алгоритм численного решения системы, состоящей из интегро-дифференциальных уравнений (8) и (10) и начального условия z ( s ,0). Численное интегрирование уравнения (10) при найденных функциях T ( s , t ) и N ( s , t ) может осуществляться по одной из стандартных схем, например, по схеме Эйлера второго порядка точности или схеме Рунге-Кутты четвертого порядка точности.

Для численного решения сингулярного интегрального уравнения (8) воспользуемся подходом, принятым в комплексном методе граничных элементов [16]. Разобьем контур L дискретным множеством точек на элементы [ z , z_{i + 1} ] ( i = 0,1,... N - 1) (Рис. 3). Ввиду замкнутости фронта вытеснения первая и последняя точки разбиения совпадают, то есть z_N = z ₀. Каждой из точек z_k соответствует значение длины дуги s k . Выберем и зафиксируем некоторую точку z k = z ( s_k ) на контуре L . Интегральное слагаемое в (8) для точки z k представим в виде суммы интегралов по элементам разбиения [ z^ , z^ _{+ 1} ]:

N + к -1 ^s i + 1

f ^{Z (} z ( ° ) ^- z k ) T ^{( о )} d ° = £ J J z ( ° ) ^- z k ^)T ( ° ) d ° .                          ⁽¹¹⁾

L                                 = к s '

Сингулярный интеграл в (11) имеет интегральное ядро в виде дзета-функции Z ( z ( о ) - z k ), то есть обладает особенностью вида 1/ ( z ( о ) - z_k ) при прохождении через точку z k контура L . В связи с этим выделим особенность в отдельное слагаемое и представим сумму в правой части (11) в следующем виде:

£^С С z ( о ) - z_k )T ( о ) d о = J z ( z ( ° ) - z_k ) T ( ° ) d ° + V - ² J z ( z ( ° ) - z_k ) T ( ° ) d ° .          (12)

i = ^k s '                                                 s k - 1                                                 i = ^{k + 1} s '

Выделив в Z(z(о) - zk.) сингулярную и регулярную составляющие, представим первое слагаемое в (12) как sk+1                                                      sk+1             1

T ( g ) d g ,

J ^{z (} z ^{( g )} - z k ) T ^{( g )} d ^G = f —---- + ^ . ⁽ z ^{( g ) -} z k )

Sk-                         Z-1 z(g) - zk да где _(z(g) - zk) = £ ' n, m =-да

¹        ₊1 ₊ ^{( z ( g ) - z}k )

( z ( g ) - z_k ) -to  to to ²

— регулярная часть дзета-функции.

s k + 1

Для вычисления в представлении (13) сингулярного интеграла J sk-1

T ( G ) ^{z ( g ) -} z_k

d g

разложим функции

z ( g ) и T ( g ) в окрестности точки s_k в ряд Тейлора и запишем его в следующем виде:

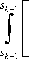
_____________1_____________ zk + zk (G sk)- zk

[ T k + T /(G

-

s k + 1 s k ) ] d ^G = J

Tk

T ' + - k- d g ,

z k J

где T_k = T ( s_k ), T k = T ‘ ( s_k ), z_k = z ( s_k ), z k = z ‘ ( s_k ). Учитывая, что сингулярный интеграл (14) в точке s_k понимается в смысле главного значения Коши, выражение (14) можно записать как

sk + 1        Т

T k

£ z k ^{( G-} s k )

sk+ k   k   skk

I —d G= — Inl-----1 + — (Sk+1 - Sk-1 ), skzk      zk   lAk-1 J zk

где A s_k = s_{k + 1} - s_k , A s_k -1 = s_k - s_k - ₁. Заменив величину T k = T ‘ ( s_k ) ее центральной конечной разностью,

преобразуем полученное выражение к виду:

т

Tk- ln z k

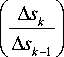
T' ,

⁺ "T^{( s}k +1

zk

—

^sk -1 ) = ¹ z_k

Г ^

T l_n ^{A s k} \ ₊ t -T

T k ln l .       I ⁺ T k +1    T k -1

y ^{A s}k -1 J

Регулярную составляющую выражения (13) с помощью формулы трапеций можно записать как

s k + 1

J                            2                                      2

^s k - 1

= - [Z * ( z_k -1 - z_k ) T k -1 A s k -1 + Z * ( z_k +1 - z k ) T k +1 A s k ] .

Таким образом, приближенная формула для вычисления интеграла (13) имеет следующий вид:

s k + 1                                                 1

J z(z(g) - zk)T(g)dG = — sk-.                                     zk

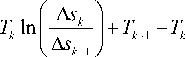
+ 2 [ Z * ( z k -1 - z k ) T k -1 A s k -1 +z * ( z k +1 - z k ) T k +1 A s k ] .

Второе из регулярных слагаемых в (12) также можно найти, применив формулу трапеций. Запишем его в виде:

N + k -2 ^s i + 1                                    1 N + k 2

£ J Z ( z ( g ) - z_k ) T ( g ) d g = - £ [ Z ( z , - z_k ) T + Z ( z , +1 - z k ) T +1 ] A s , .                  (16)

/ = k +1 s-                                       ² , = k +1

Объединяя формулы (15) и (16), приходим к итоговому выражению для сингулярного интеграла (11):

J ^{z (} z ^{( g ) -} z k ) T ^{( g )} d ^G =

L                            z k

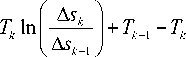
1 N + k -2

⁺ 2 ^{[ Z}* ⁽ z k -1

- z . ) T . ,A s . ,+Z.( z_k ,- z . ) T . .A s . 1+— V [Z( z k у k -1 k -1    ”* v k +1 k у k +1 k J                L ,

² , = k +1

- z k ) T +Z ( z , +1 - z k ) T +1 ] A s , .

Учитывая, что в выражении (17) значения T_k , и T_{k + 1} функции T ( s ) присутствуют в каждом из трех слагаемых, перепишем последнее слагаемое в нем следующим образом:

1 N+к-2                                                1 N+к-21

т Ё [Z(Zi -Zk)T + Z(zM -zk)T+1 ]Asi = - Ё [Z(Zi -Zk)T]Asi + -Z(Zk+1 -Zk)T.\'к+i

• 2    i = к+1                                                 2 i = к+2

1 N+к-2

⁺ Т Ё E ^{Z ( Z}j ^{- Z}k ) ^Tj ] ^{A 5}j -1 ⁺t"^{Z( Z}N + к -1 ^{- z}k ) ^TN + к l^{A s} N + к -2 ’

2 j=к+2

где j = i + 1, а величины с индексами N + к — 2, благодаря замкнутости контура L , совпадают с величинами с индексами к — 2 и так далее. Принимая во внимание это замечание, запишем итоговую квадратурную сумму, сгруппировав по значениям искомой функции T_k :

1 N+к -2                                                 1 N+к -2

- Ё [ Z ( z i - Z k ) T + Z ( Z +1 - Z k ) T +1 ] A s i = - Ё Z ( Z-Z_k ) T ( A s i +A s i —, ) +

² i = к +1                                                  ² i = к +2

+ 2 z ( Z k +1 - Z k T A к +1 + 2 z ( Z k -1

- z_k )T -1 A s -2 .

Подставим данное представление в формулу (17), сгруппируем все коэффициенты при значениях T_k , и T_{k + 1}. В результате получим соотношение (17) в следующем виде:

6^{z ( Z ( a ) — Z}k ^{) T ( a )} d G = ² T k 1П I ^{2 s} - I ⁺ T k +1

J                         7        Av

L                         ^Zk      V ^A к -1 7

² + ¹ Z ( Z k +1 - Z k ) A s к +1 + ¹ Z * ( Z k +1 ^Zk   ^{2                   2}

—

^Zk ^{) A 5} к ⁺

⁺ T k -1

^{— 2 + 1 Z ( Z}k -1 ^{— Z}k ^{) A 5}к -2 ^{+ 1 Z}* ^{( Z}k -1 ^{— Z}k ^{) A 5}к -1

^Zk   ^{2                    2}

1 N + к -2

+ т Ё ^{z (} Z - ^Zk ) T ^{( A s}i ^{+A s}i -1 ⁾.

² i = к +2

Функция Z * ( z — Z_k ) отличается от Z ( z — z_k ) на величину 1/ ( z — z_k ) . Поэтому дополним величины

Z . ( Z_{k + 1} - Z_k ) и Z * ( Z_k -1 - Z_k ) до значений Z ( z_{k + 1} - z_k ) и Z ( z_k -1 - z_k ) и перепишем формулу как

f Z ( Z ( a ) - Z k ) T ( a ) d g = ² T k In I "^{A 5} ^ I + T k +1

^J                        7 Av

L                           z k      V^ к -1 7

+ T k -1

1    1    A s_k .

—

^Zk   ^{2 Z}k -1^{- Z}k.

1   1    A s _k

^Zk   ^{2 Z}k +1^{- Z}k _

1 N + к -1

⁺ 7- Ё ^{Z ( Z}i - ^Zk ) T ^{( A s}i ^{+A s}i -1 ).

² i = к +1

В данном выражении слагаемые A s_к (zz_{k + 1} - z_k ) и A s_{k - 1}/( z_k , - z_k ) представляют собой правую и левую

конечные разности производной dsjdz в точке z_k . Следовательно, окончательная аппроксимация этого

интеграла будет иметь следующий вид:

<£ ^{z (} z ^{( a ) -} z k ^{)T ( a )} d ^a = T²

L                          ^{2 Z}k

( A.S¹. ^

2 T k In i — ^ ^ I + T +1 - T -1 V ^{A s}k -1 7

N + к -1

+ Ё z(zi- zk)T (Asi+Asi-1)zk i=к+1

Вернемся к исходному интегральному уравнению (8), вещественную и мнимую часть которого для выбранных на контуре L точек z_k = z ( s_k ) можно записать как

1 +^ T ( s k ) = Re J Ф ( s k ) +          z ( a ) - z_k)T ( a ) d a

2                  I              2 n i

N ^{( s}k ) = Im ф ^{( s}k ) ⁺ ^t^ ²^ ^{z ( a ) - z}k ^{) T ( a ) d a z}k ’ . I               2 n i

Как следует из уравнений (19), вещественная часть, учитывающая аппроксимацию (18), представляет собой систему линейных алгебраических уравнений для нахождения значений искомой функции T(s, t) в заданный момент времени tn на дискретном множестве точек z(sk) = zk. Мнимая же часть при найденных значениях Tk , также учитывающая аппроксимацию (18), является, по сути, формулой для вычисления значений функции N(s,t) в заданный момент времени tn на этом же дискретном множестве точек.

Полученные значения T_k и N_k используем далее при расчете перемещений точек z_k за промежуток времени [ t n ,t n +1 ] . Данные перемещения z k определяются из численного решения задачи Коши (10) с помощью метода Рунге–Кутты, модифицированного с учетом комплексной природы дифференциального уравнения (10). В качестве переменной интегрирования выберем безразмерное время т , которое связано с исходной временной переменной t как т = 10 -4 Qt[^2 п mh ю 2 ) .

4.    Результаты расчетов

Итогом решения рассмотренной задачи стал программный комплекс, позволяющий как отслеживать эволюцию границы контакта воды и нефти во времени, так и количественно оценивать эффективность той или иной схемы заводнения. Результаты работы программы представляются изображениями текущего положения заполненной водой области, а также такими числовыми характеристиками процесса, как время начала обводнения добывающих скважин и коэффициент охвата заводнением ( K _охв), характеризующий момент появления воды в ближайших к нагнетательной скважине добывающих скважинах.

В рамках настоящего исследования проведен вычислительный эксперимент, целями которого стали как сравнительный анализ различных схем заводнения, так и оценка влияния разности вязкостей фильтрующихся фаз на эффективность вытеснения нефти водой. В процессе расчетов проводилось как визуальное сравнение картин заводнения области, так и сравнение указанных выше числовых параметров.

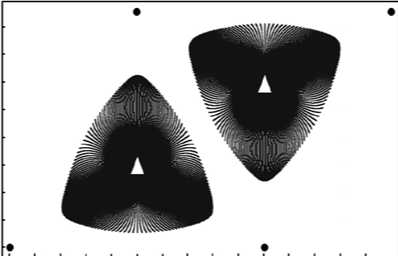
Рассмотрены лобовая рядная, четырехточечная, пятиточечная, семиточечная и девятиточечная схемы заводнения. Для мониторинга текущего положения фронта вытеснения было задействовано 180 трассеров, то есть 180 траекторий движения воды, выходящих в начальный момент времени под углами 9 = (1, 2,... 180)п/90 из нагнетательной скважины (граничное условие для уравнения (10)). Положение заводненной области (трассеры выделены черным цветом) для четырехточечной схемы заводнения при значении коэффициента мобильности к = 1 изображено на рисунке 4 для двух значений времени: т = 0,0732 и момента прорыва воды в скважину т = 0,1025.

0,9 0,8 0,7 0,6 0,5

0,4 0,3 0,2 0,1

0     0,2    0,4    0.6    0,8     1,0    1,2    1,4

0,9

0,8

0,7

0,6

0,5

0.4

0,3

0.2

0,1

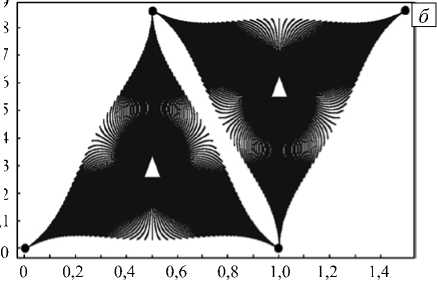
Рис. 4. Положение заводненной области, образованной 180 трассерами (выделены черным цветом), для четырехточечной схемы заводнения при к = 1 в момент времени т = 0,0732 ( а ) и в момент прорыва воды в скважину при т = 0,1025 ( б ); добывающие скважины показаны черными точками, нагнетательные – треугольниками

Коэффициент охвата заводнением ( K _охв ) — одна из важнейших числовых характеристик процесса. Этот параметр определяется как отношение площади зоны, заполненной водой, к площади всего рассматриваемого участка. Он позволяет выявить так называемые «целики» нефти — те участки пласта, которые при выбранном расположении скважин не содержат воды к началу процесса обводнения добывающих скважин.

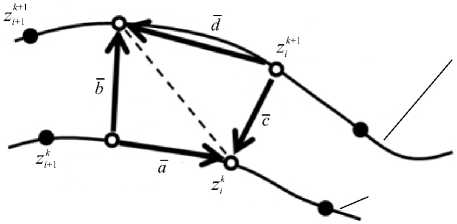
Алгоритм нахождения ( K _охв) описан в работе [5] и заключается в следующем. На основании того, что фронт вытеснения остается гладким вплоть до начала обводнения добывающих скважин, заводненный на отрезке времени [ t k , t k _{+ 1} ] участок аппроксимируется набором четырехугольников, построенных на точках z_t и z_{t + 1} в моменты времени t k и t k _{+ 1} (Рис. 5). Площадь заводненной области определяется путем суммирования площадей получаемых четырехугольников, которые в свою очередь разбиваются на составляющие их треугольники (площади S ₁ и S ₂ на рисунке 5), а площадь последних вычисляется по правилам векторного произведения.

Позиция фронта вытеснения в момент времени t_k

Позиция фронта вытеснения в момент времени t_k._x

^+^+|(|axft|+|cxrf|)

Рис. 5. Схема для расчета площади заводненной области за отрезок времени [ tk , t_k + ]

Известно [17], что отношение вязкостей к оказывает негативное влияние на количественные показатели нефтеотдачи: с уменьшением параметра к , при сохранении прочих равных условий разработки, наблюдается уменьшение объемов извлекаемых нефтяных запасов из-за растущей нестабильности вытеснения нефти водой. Кроме того, при определенных значениях к возникает неустойчивость Саффмана–Тейлора [18, 19], которая часто называется «вязким пальцеобразованием» [20, 21]. При существенном различии вязкостей нефти и воды (то есть отличии величины к от единицы) происходит нарушение устойчивости фронта вытеснения, в результате чего нагнетаемая вода как бы «пронзает» нефтяную область вытянутыми мысами (пальцами), оставляя за собой неосвоенные нефтяные запасы. Подобный эффект также был обнаружен в ходе проведенных численных экспериментов: при определенных значениях параметра к наблюдалось нарушение гладкости фронта вытеснения с последующим образованием «вязких пальцев». Указанный эффект изображен на рисунке 6 для случая пятиточечной обращенной схемы заводнения (здесь трассеры изображены белым цветом на черном фоне). Для сравнения рисунок 6 дополнен картиной заводнения, полученной другими авторами экспериментально для аналогичной геометрии расстановки скважин (см. рисунок 6 а в работе [22]).

Рис. 6. Нарушение устойчивости фронта вытеснения для пятиточечной обращенной схемы расстановки скважин: численный расчет при значениях к = 1/5 и т = 0,0450 (заводненная область образована 180 трассерами, изображенными белыми линиями на черном фоне) ( а ), данные из работы [22] ( б )

Необходимо подчеркнуть, что изучение эффекта «вязкого пальцеобразования» не являлось предметом настоящего исследования: указанная проблема требует большего внимания к вопросам неустойчивости фронта вытеснения и будет рассмотрена отдельно в последующих работах.

Часть результатов численного мониторинга фронта вытеснения представлена ниже. Так, на рисунке 7 изображена заводненная область для семиточечной и девятиточечной обращенных схем расстановки скважин в момент прорыва воды в добывающую скважину при различных отношениях коэффициента мобильности к : на картинах представлены окрестности добывающих скважин (белые точки), в сторону которых движется фронт вытеснения (траектории частиц воды обозначены белыми линиями). При сравнении изображений наблюдается похожесть в характерах изменений форм мысов, образуемых нагнетаемой водой, причем это имеет место для всех исследованных схем заводнения.

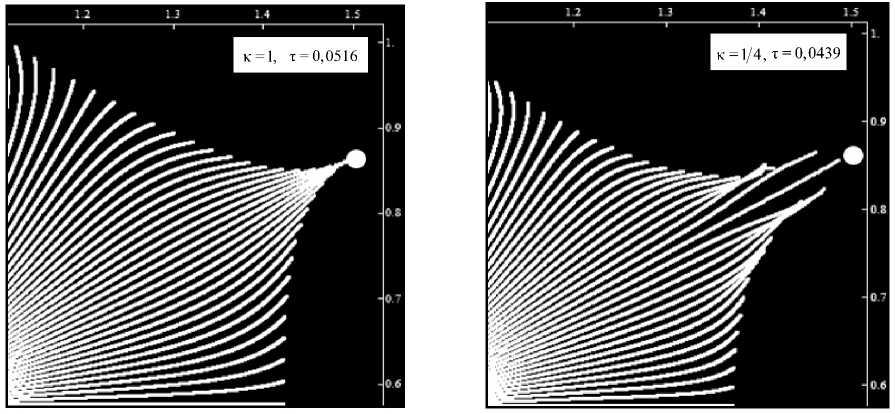
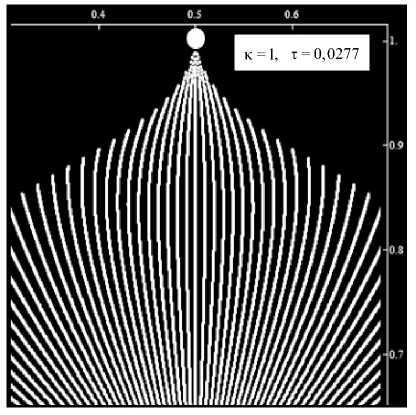
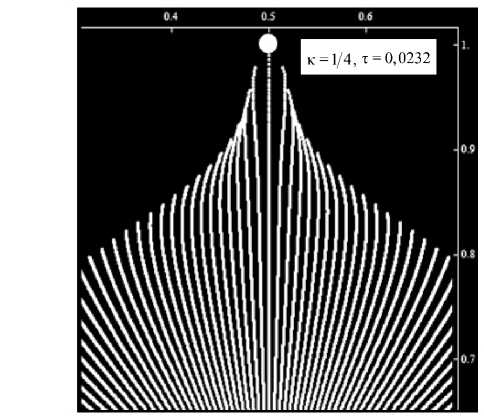
Рис. 7. Картины заводненной области в момент прорыва воды в скважину, образованные 180 трассерами (показаны белыми линиями) для семиточечной и девятиточечной обращенных схем заводнения при различных значениях параметра κ и безразмерного времени τ (добывающие скважины обозначены белыми точками)

В таблице 1 содержатся значения времени начала обводнения τ , рассчитанного для четырех схем заводнения при различных значениях вязкостей нефти и воды κ . Результаты определения коэффициента охвата заводнением K _охв отражены в таблице 2. Аббревиатура VF (viscous fingers) указывает на появление «вязких пальцев» для выбранной схемы расстановки скважин при заданном отношении вязкостей; вследствие нарушения гладкости фронта вытеснения найти K _охв для данного значения κ невозможно. Для большей наглядности столбцы таблицы 2 дополнены значениями, взятыми из монографии Ф. Крэйга [17] для случая κ= 1.

Таблица 1. Значения τ при различных значениях коэффициента мобильности κ

Схема заводнения	Значения τ при различном отношении вязкостей κ
	κ= 1	κ= 12	κ= 13	κ= 14
Пятиточечная обращенная	0,1152	0,1017	0,0960	VF
Лобовая рядная	0,1820	0,1500	VF	VF
Семиточечная обращенная	0,0516	0,0472	0,0452	0,0439
Девятиточечная обращенная	0,0277	0,0252	0,0240	0,0232

Таблица 2. Значения K охв при различных значениях коэффициента мобильности к

Схема заводнения	Значения K охв при различном значении коэффициента мобильности к
	к = 1 (Ф. Крэйг)	к = 1	к = 12	к = 13	к = 14
Пятиточечная обращенная	70%	72,5%	63,5%	60%	VF
Лобовая рядная	58%	57,2%	47%	VF	VF
Семиточечная обращенная	73%	75,2%	68,5%	65,3%	63,3%
Девятиточечная обращенная	55%	52,7%	48%	45,5%	44%

Визуальный анализ картин заводненной области показал качественное совпадение результатов настоящего исследования с данными других авторов, полученными как при численном моделировании [23], так и в рамках физического эксперимента [6]. Результаты численного эксперимента подтверждаются также сделанными ранее другими авторами [17] выводами об отрицательном влиянии высокой разницы вязкостей воды и нефти на конечную нефтеотдачу. При численном эксперименте было получено, что с уменьшением значения коэффициента мобильности к наблюдается как сокращение «безводного» периода добычи, так и площади, охватываемой заводнением, что негативно сказывается на величине K _охв и, следовательно, на объеме извлекаемых запасов нефти.

5.    Выводы и пути развития исследования

Настоящее исследование является продолжением работы [5] и обобщает ранее полученные результаты на случай поршневого вытеснения нефти водой, при котором физические свойства жидкостей полагаются различными. Итогом проделанной работы стал программный комплекс, функции которого во многом аналогичны его предшественнику [5]: основанная на решении задачи мониторинга фронта вытеснения программа предоставляет как графические данные (картины заводненной области), так и значения числовых характеристик (время прорыва воды т , K _охв) для выбранной схемы расстановки скважин.

Разработанный программный комплекс представляет собой инструмент для сравнительного анализа различных схем заводнения при неизменных геофизических параметрах пласта: данные анализа могут применяться при проектировании разработки реальных месторождений в качестве рекомендаций к выбору схемы расстановки скважин из числа возможных вариантов, зависящих от геофизических особенностей нефтеносного участка. При этом учет физических различий совместно фильтрующихся фаз (нефти и воды) заметно приближает моделируемый процесс к реалиям нефтедобычи.

Возможности программного комплекса могут быть расширены в будущем. При дальнейшем развитии построенного представления о фильтрации воды и нефти в двоякопериодической области данные при переходе к модели двухфазной фильтрации могут быть уточнены и их количество увеличено при допущении переменных дебитов закачки вытесняющего агента (воды). Информация о процессе фильтрации для выбранной схемы заводнения также может быть дополнена прогнозами об изменениях таких характеристик производительности скважин и пласта, как суммарный дебит добычи, среднее пластовое давление, а также давление в призабойных зонах скважин.

Работа выполнена в рамках тематического плана НИР СамГТУ, финансируемого Минобрнауки России из федерального бюджета, а также при финансовой поддержке РФФИ (проект 14-01-97041-р_поволжье_а).