Моделирование и оценка параметров позиционирования совмещенной топологии навигации и связи подвижных объектов

На точность определения местоположения подвижного объекта (навигационной аппаратуры потребителя) влияют как внешние деструктивны воздействия, так и внутренние, связанные, в частности, с топологий построения системы. Показателем топологии с точки зрения определения местоположения подвижного объекта является геометрический фактор (ГФ) или коэффициент геометрии. При реализации услуги позиционирования на основе топологии системы связи с подвижными объектами (ПО) возникает задача построения рациональной совмещенной топологии систем, обеспечивающей максимальное значение геометрического фактора при выполнении требований к связи. Вопросу оценки геометрического фактора различных топологий системы связи с подвижными объектами и посвящена данная статья.

Постановка задачи

Допустим, что местоположение подвижного объекта в радионавигационной системе (РНС) оценивается на основе измерения трех радионавигационных параметров (РНП): Р 1 , Р 2 , Р з - каждый из которых измеряется с ошибками. Пусть среднеквадратичное отклонение (СКО) ошибок измерения

РНП равны соответственно ст, , ст₂ , Q₃. Поскольку ошибка при измерении РНП вызывает смещение соответствующей плоскости положения , то она в оценивании местоположения определится смещением точки пересечения всех трех плоскостей положения . Причем степень смещения плоскостей зависит от количества опорных станций (ОС) РНС, топологии их размещения в рабочей зоне и методов измерения местоположения ПО. Обобщающим косвенным параметром оценки точности определения местоположения в РНС, учитывающим данные факторы является ГФ системы [1, 2, 3, 4]. Поэтому задачу оценки точности позиционирования ПО можно сформулировать следующим образом. Исследовать распределение геометрического фактора РНС в пространстве, состоящей из трех опорных станций, размещенных в заданной рабочей зоне со следующими методами измерения РНП: дальномерный; разностно-дальномерный; псевдодальномерный.

Для расчета предлагается структура модели оценки точности позиционирования ПО, представленная на рисунке 1. Модель реализует матричный способ оценки путем определения производных по направлениям и вычисления следа ковариационной матри- цы с учетом корреляционных взаимосвязей пространственных координат измеряемой точки и координат ОС.

В представленной модели блок «f» моделирует навигационные функции в точке fj, после чего, в блоке «G» от данной функции берутся частные производные и формируется матрица G, затем перемно- жаются матрица G на транспонированную в блоке «Gt» матрицу и в блоке «tr» вычисляется след полученной матрицы, характеризующую величину геометрического фактора в виде графика. Для получения численных значений используем блок «Display».

nj| |                 eif| ini                   in^                 inl||                 жй.

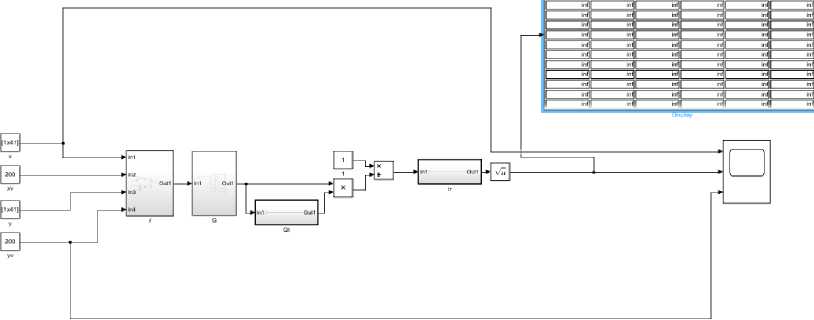
Рис. 1. Модель расчета геометрического фактора

Исходные данные для расчетов: координаты ведущей ОС – x в =20 км, y в =20 км; рабочая зона задана декартовой прямоугольной системой координат 40х40 км, шаг дискретизации – 0,1 км.

Дальномерный метод

В соответствии с моделью расчет геометрического фактора производится по выражению (1) [2]:

r= tr {(G G )-1}

- dfl где G = dx df2 dx df3 - dx d/11

dy df 2 dy df 3

dyA

G

транспонированная матрица   G ;  tr{ - }- след матрицы, f =

^(x t -x)² + (y t -y)² , i = 1, 2, 3.

Результаты расчета представлены в таблице 1.

Таблица 1. Результаты расчета ГФ с использованием дальномерного метода

№ п/п	γ º	Площадь зон равных ГФ, км2				Координаты ОС, км, ( x , y)
		ГФ=1	ГФ=2	ГФ=3	ГФ=4	ОС 1	ОС 2
1	15	0	35,32	85,6	154,43	(19.608, 22.974)	(20.392, 22.974)
2	50	0	45,22	109,2	198,53	(18.372, 22.719)	(21.268, 22.719)
3	90	0	68,05	161,98	293,88	(17.879, 22.121)	(22.121, 22.121)
4	120	0	88,34	207,1	371,8	(17.402, 21.5)	(22.598, 21.5)
5	180	0	106,86	253,34	453,94	(17, 20)	(23, 20)

На рисунках 2-5 представлено графическое отображение геометрического фактора зависимости от топологии РНС.

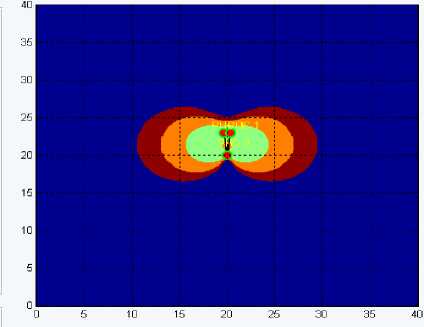
Рис. 2. Графическое отображение ГФ

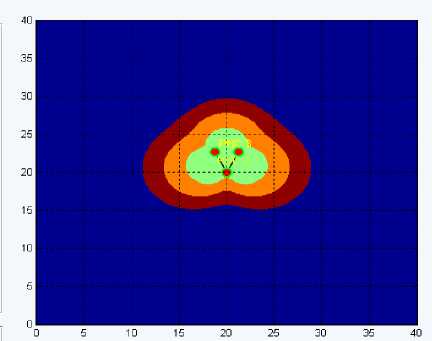
Рис. 3. Графическое отображение ГФ при

при у =15 °

Y =50 °

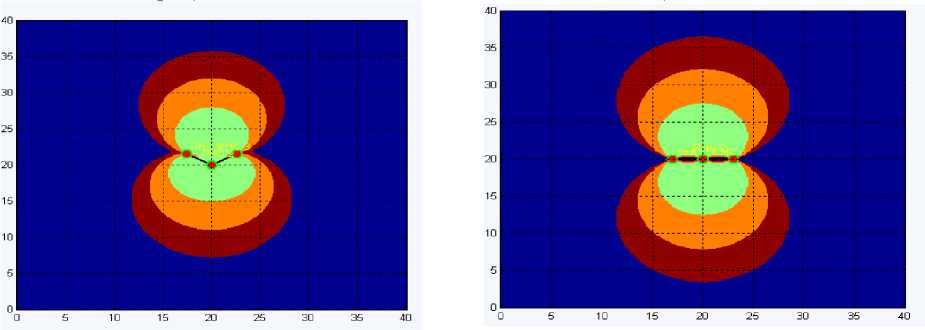
Рис. 5. Графическое отображение ГФ при при y=120°

Рис. 4. Графическое отображение ГФ

Y=180°

Предложения и рекомендации по использованию метода

Анализ результатов расчетов, выполненных для ранее приведенных данных, позволяет сделать следующие выводы:

• 1.    С увеличением углов обзора ОС увеличивается зона обслуживания ПО. Максимальная площадь зоны образуется при угле между базами системы равными 180º и равна 453 км², при ГФ меньше 3.

• 2.    При углах баз более 70º зоны располагается в I и III секторах, при этом при γ=180º получаем максимальную площадь зоны равного ГФ.

• 3.    Типовое значение ГФ составляет примерно 3, т.е. данный метод ухудшает инструментальную погрешность не более чем в 3 раза для выбранных размеров топологии.

Разностно-дальномерный метод при 6 =

[d/i d/il dxdy d/2   d/2

dxdy

Расч ет ГФ произв одит ся по выражен ию (1)   [2]

f j = V^(% i -^x)2 + ⁽У 1 -У)² + V^(% 2 - x⁾² + ⁽У 2 — У⁾² при i= 1^3.

Результаты расчета представлены в таблице 2.

Таблица 2. Результаты расчета ГФ при разностно-дальномерном методе

№ п/п	γ º	Площадь зон равных ГФ, км2				Координаты ОС, км, ( x , y)
		ГФ=5	ГФ=10	ГФ=15	ГФ=20	ОС 1	ОС 2
1	15	4,9	9,67	13,83	17,78	(19.608, 22.974)	(20.392, 22.974)
2	50	16,41	27,18	36,98	47,08	(18.372, 22.719)	(21.268, 22.719)
3	90	26,44	46,95	66,75	86,08	(17.879, 22.121)	(22.121, 22.121)
4	120	33,04	65,52	97,34	128,82	(17.402, 21.5)	(22.598, 21.5)
5	180	39,5	92,8	143,86	194,62	(17, 20)	(23, 20)

На рисунках 6-9 представлено графическое отображение геометрического фактора в зависимости от топологии РНС.

Предложения и рекомендации по использованию метода

Анализ результатов расчетов, позволяет сделать следующие выводы:

• 1.    В случае равных длин баз РНС геометрия распределения геометрического фактора в плоскости симметрична относительно прямой, проведенной по биссектрисе угла, образованного базами.

• 2.    В случае неравенства длин баз РНС при угле между базами 0º и 180º площади зон равных ГФ примерно равно, но ярко выражается неравномерность распределения изолиний ГФ. Данное обстоятельство позволяет путем выбора ведущей ОС оперативно изменять зону действия РНС.

• 3.    Типовое значение ГФ составляет примерно 2, т.е. данный метод ухудшает инструментальную погрешность не более чем в 2 раза для выбранных размеров топологии.

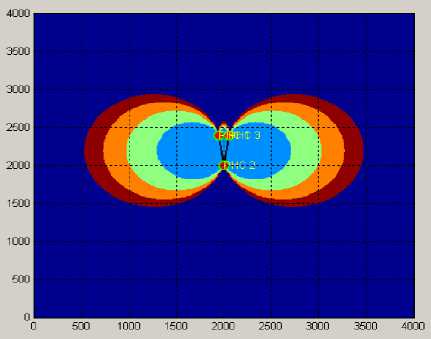
Рис. 6. Графическое отображение ГФ при у =15 °

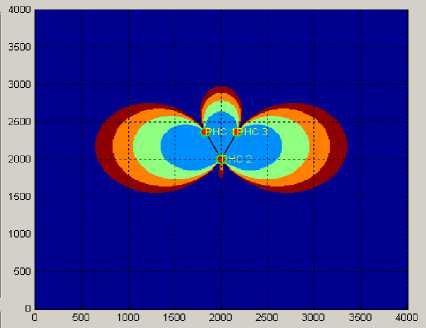
Рис. 7. Графическое отображение ГФ

=50°

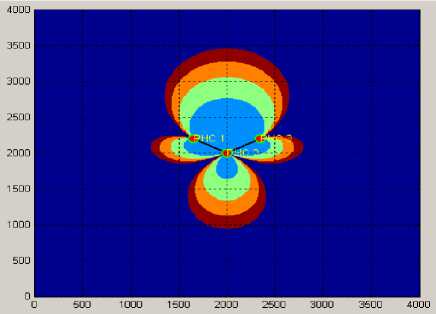
Рис. 8. Графическое отображение ГФ при

Y =120 °

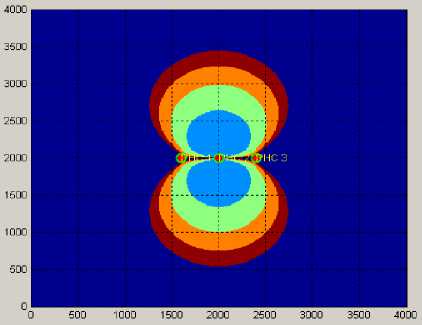
Рис. 9. Графическое отображение ГФ при

Y=180°

Псевдодальномерный метод

Расчет ГФ производится по выражению (1)

f j = 7⁽^-^хУ + (y t —y)² + 7(^ 2 -^)² + ⁽У 2 —У⁾².

	- df i	dfi-
	dx	dy
	df2	df 2
[2]   при G =	dx	dy
	df 3	df 3
	- dx	dy -

Результаты расчета представлены в таблице 3.

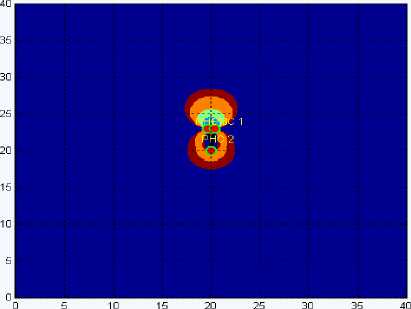
На рисунках 12-16 представлено графическое отображение геометрического фактора в зависимости от топологии РНС.

О 5       10      15      20      25      30      35      40

Рис. 12. Графическое отображение ГФ при

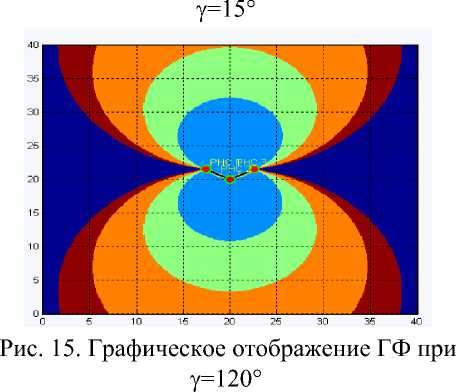
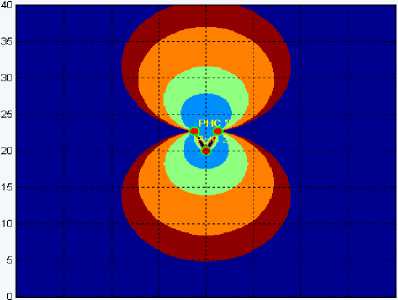
Рис. 13. Графическое отображение ГФ

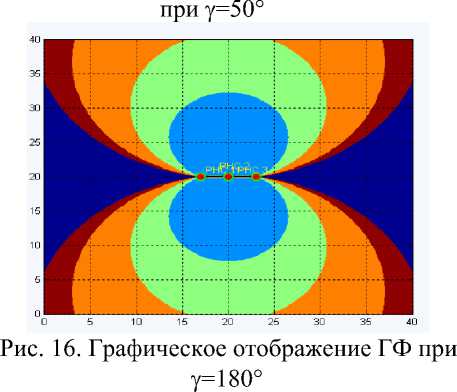
Предложения и рекомендации по использованию метода

Анализ результатов расчетов, позволяет сделать следующие выводы:

• 1.    Максимальная площадь зоны образуется при угле между базами равным 180º и равна 1314 км при ГФ менее 3.

• 2.    При всех углах расположения баз относительно друг друга наблюдается то, что

• 3. Типовое значение ГФ составляет около

Таблица 3. Результаты расчета ГФ при псевдо дальномерном методе

№ п/п γ º Площадь зон равных ГФ, 106 км2 Координаты ОС, км, (x, y) ГФ=3 ГФ=5 ГФ=8 ГФ=10 ОС1 ОС2 1 15 2,38 6,42 23,34 42,81 (19.608, 22.974) (20.392, 22.974) 2 50 39,43 123,02 321,24 501,19 (18.372, 22.719) (21.268, 22.719) 3 90 125,76 354,09 346,13 489,33 (17.879, 22.121) (22.121, 22.121) 4 120 191,64 533,58 389,75 512,43 (17.402, 21.5) (22.598, 21.5) 5 180 257,48 702,68 421,54 626,34 (17, 20) (23, 20) основные части зоны концентрируются в I и III секторах.

Результаты исследований показывают, что наилучшим методом определения местоположения ПО по показателю ГФ явля-

5, т.е. метод ухудшает инструментальную погрешность не более чем в 5 раз для выбранных размеров топологии.

Заключение

В работе разработана модель оценки

ется разностно-дальномерный метод. При этом ГФ изменяется от 2 до 3 в зависимости от топологии размещения опорных станций в рабочей зоне. В связи с этим возникает следующая задача, заключаю-

точности позиционирования, которая является универсальным и объективным инструментом для проведения сравнительной оценки различных способов позицио-

щаяся в оптимизации топологии опорных станций РНС для получения наименьшего значения геометрического фактора системы [5].

нирования радионавигационных систем.