Моделирование и прогнозирование динамики курсов финансовых инструментов с применением эконометрических моделей и фрактального анализа

Функционирование современной рыночной экономики невозможно без привле- чения и перераспределения капиталов. Од- ним из основных механизмов для решения этих задач является финансовый рынок. Финансовые рынки как система сложны и неустойчивы, а протекающие на них процессы, в частности динамика изменений ценовых котировок финансовых инструментов, стохастичны [ 1 ]. Природа этой стохастики очевидна, ведь на курсы финансовых инструментов влияет огромное количество различных факторов - экономических, психологических (настроения и ожидания участников рынка), природных, политических и т. д. Этих факторов настолько много, что ни одна модель не в состоянии учесть их все. Срабатывает философский принцип перехода количества в качество, и создается впечатление, что динамика ценовых приращений хаотична и непредсказуема.

В то же время задача прогнозирования будущих значений курсов финансовых инструментов является актуальной, поскольку возможность формирования достаточно точных предсказаний позволила бы снизить риски и увеличить доходность от операций на рынках. Существует много подходов к решению этой задачи: фундаментальный и технический анализ, стати- стическое и эконометрическое моделирование, различные методы машинного обучения, такие как нейросетевой анализ [2], эконофизические подходы (фрактальный, p-адический анализ [1]) и др., но их эффективность и применимость в тех или иных условиях остается предметом дискуссии и исследований, во многом потому, что сама природа динамики финансовых рынков вызывает споры. Нет единого мнения, является ли процесс ценовых изменений полностью случайным (стохастическим) и потому принципиально непредсказуемым или же это процесс детерминированный: поведение цен зависит от конечного числа каких-то конкретных факторов и поддается моделированию.

Классические методы анализа финансовых рынков, такие как модель опти- мального инвестиционного портфеля Г. Марковица, модель САРМ У. Шарпа и модель ценообразования опционов Блека -Шоулза, основаны на предположении Л. Башелье о том, что характеристики финансовых активов являются случайными величинами, распределенными по нормальному закону [3]. Теоретической базой, воплощающей данный постулат, является предложенная экономистом Ю. Фама гипотеза эффективного рынка (Efficient Market Hypothesis, EMH) [4], суть которой состоит в том, что вся значимая информация немедленно и в полной мере отражается в ценах, они являются практически непредсказуемыми, а их динамика описывается моделью «случайного блуждания». Соответственно, исследовать данные процессы возможно методами вероятностного подхода.

Однако крупнейшие финансовые кризисы (такие как кризис 2008 г., превратившийся в мировой экономический) не вписываются в постулаты данного подхода. В 1987 г. случился обвал американского рынка, за один день индекс Доу-Джонса упал на 29,2% [3] . Согласно кривой Гаусса такое событие должно происходить раз в миллионы лет. Однако последовали и другие кризисы, вследствие чего стало понятно, что гипотеза эффективного рынка не является универсальной. Было обнаружено, что в нестабильные периоды кривая плотности распределения изменения доходностей не соответствует гауссовской и риск наступления больших отклонений значительно (на 5 и более стандартных отклонений) превышает таковой при нормальном законе. Такие распределения получили названия распределений с «толстыми хвостами» ( fat tails ). Их форма свидетельствует о том, что динамика рыночных процессов не всегда является случайной.

Когда стало очевидным, что классический подход к пониманию принципов развития финансовых рынков не в состоянии объяснить кризисные явления, исследователи начали искать другие подходы и пытаться применять к анализу экономических процессов неортодоксальные методы, ранее для экономики не характерные. Вклад в развитие экономической науки внесли ученые из таких областей знания, как военное дело (опционы, теория игр, логистика, исследование операций), биология (нейронные сети), информатика (информационные технологии), а также физика [5]. В физике хорошо изучено поведение неупорядоченных стохастических систем; оттуда в экономику пришли такие понятия, как «броуновское движение» и «случайное блуждание», относящиеся к поведению элементарных частиц [1]. Наука, которая использует типичные для физики методы исследований для изучения экономических систем, называется эконофизикой1.

Одним из методов эконофизики является фрактальный анализ – перспективное (о чем свидетельствует достаточно большое количество зарубежных публикаций), но недостаточно представленное в отечественной научной литературе [7] направление исследования финансового рынка. Основателем его стал американский математик Б. Мандельброт, предположивший, что динамика рынков подчиняется степенным законам [3]. Он выдвинул концепцию, альтернативную EMH, – гипотезу фрактального рынка (Fractal Market Hypothesis, FMH), согласно которой процесс ценообразования на рынках не случаен, а глобально детерминирован, прошлые цены влияют на будущие, а рынки обладают фрактальными свойствами. Наличие этих свойств объясняется тем, что для устойчивости рынка на нем должны присутствовать инвесторы с разными инвестиционными горизонтами (от нескольких часов до нескольких лет) [8]. Если рынок имеет один горизонт инвестирования, на нем возникает нехватка ликвидности и, как следствие, паника [9]. Фрактальность финансовых рядов выражается в таком их свойстве, как «долгая память» (long memory), или персистентность. Это свойство процесса поддерживать тенденцию изменения. Автокорреляционная функция персистентного ряда убывает гиперболически медленно. Персистентные процессы характеризуются независимостью от вре- менного масштаба: дневные приращения зависят от прошедших дневных приращений в той же степени, что и недельные от прошедших недельных [6]. Существуют расширения авторегрессионных стохастических моделей временных рядов, учитывающие свойство долгой памяти [2], и, согласно утверждениям ряда исследователей, такие модели позволяют получать более точные прогнозы [10; 11].

Применению фрактального анализа к задаче прогнозирования динамики финансовых рынков посвящены немногочисленные исследования. Так, в работе Е.С. Остапенко и Т.А. Дунаевой [12] установлено, что на ценах акций компании Google модель с долгой памятью ARFIMA дает меньшую ошибку прогноза, чем ARMA. М.В. Прудский [10] использовал ARFIMA для моделирования курса доллара к рублю, им были сделаны выводы о том, что модель обладает способностью делать краткосрочные прогнозы и является более точной в сравнении с другими статистическими моделями из-за учета ею фрактальных свойств. И.И. Белолипцевым и С.А. Фар-хиевой [13] был предложен подход к прогнозированию финансовых рядов на основе нейросетевой модели, одним из предикторов которой явился индекс фрактальности, и на примере курсов акций ОАО «Татнефть» было показано, что его использование улучшает прогностические свойства модели. Тем не менее применение фрактальных методов прогнозирования на финансовых рынках изучено недостаточно: единичны примеры успешных предсказаний, полученных с помощью таких моделей; отсутствуют работы, акцентирующие внимание на сравнении фрактальных и нефрактальных моделей на достаточно больших массивах ценовых данных, что не позволяет с уверенностью утверждать о превосходстве моделей, учитывающих фрактальные свойства рядов. Этим обусловлена актуальность данного исследования.

Основная гипотеза исследования заключается в следующем: учет фрактально-сти финансовых рядов при прочих равных условиях позволяет получать более точные прогнозы динамики курсов финансовых инструментов. Целью исследования является проверка этой гипотезы. В качестве методического инструментария выбран фрактальный анализ, эконометрические модели ARIMA, GARCH и их фрактальные модификации, учитывающие свойство долгой памяти анализируемых процессов. Предмет исследования – динамика курсов инструментов, обращающихся на российском финансовом рынке, а также фондового индекса (на примере индекса ММВБ).

Приступим к достижению поставленной цели и начнем с обзора результатов ранее проведенных исследований.

Теоретический обзор

З адачей применения фрактального подхода к анализу финансовых рынков и прогнозированию курсов финансовых инструментов занимались отечественные и иностранные авторы. Результаты обзора некоторых актуальных научных работ в данной области представлены в табл. 1.

Таблица 1

Научные работы по фрактальному анализу финансовых рынков

Ключевые достижения	Авторы	Подходы (методы)	Результаты
Подтвержден фрактальный характер финансовых временных рядов	Ю.М. Балагула [14]	R/S-анализ, спектральный метод (GPH)	Выявлено наличие долгой памяти в рядах биржевых оптовых цен на электроэнергию и фондовых индексов разных стран
	А.В. Зиненко [3]	R/S-анализ
	G. Caporale, M. Škare [15]	R/S-анализ, спектральный метод (GPH), ARFIMAFIGARCH-моделирование	Выявлено наличие двойной длинной памяти (как в рядах доходности, так и в рядах волатильности) реального ВВП Великобритании
	S. Zhelyazkova [16]	ARFIMA-FIGARCH, HY-GARCH и FIAPARCH-моделирование	Выявлено наличие двойной длинной памяти в курсах двенадцати валют к доллару США; установлено, что динамика различных валютных пар хорошо описывается различными фрактальными модификациями GARCH-моделей
Предложены новые фрактальные показатели: размерность минимального покрытия и индекс фрак-тальности	Н.В. Старченко, М.М. Дубовиков [17]	Метод минимального покрытия, R/S-анализ, клеточный метод	Выявлено, что для определения индекса фрактальности требуется на два порядка меньше данных, нежели для оценивания показателя Херста методом R/S-анализа (на примере цен акций тридцати компаний, входящих в индекс Доу-Джонса)
Выполнено сопоставление различных фрактальных показателей, показано, что они согласованы, но отличаются точностью	Е.К. Кривоносова и др. [18; 19]		На примере цен акций Лукойл установлено, что наиболее точно фрактальная размерность определяется методом клеточного покрытия
Обоснована возможность применения фрактального анализа для предсказания кризисных ситуаций объектов разного уровня	А.К. Мансуров [20]	Метод ДФА	Выявлено, что существенное отклонение фрактальной размерности рядов валютных курсов сигнализирует о валютных кризисах (на примере курсов двадцати трех валют к доллару США)
	Е.К. Кривоносова [2]	Фрактальные (R/S-анализ, методы клеточного и минимального покрытия) и мультифрактальные (МФ-ДФА, вейвлет-преобразования, анализ с использованием показателя Гельдера) методы	Показано, что наиболее точным для определения стабильности работы предприятия из фрактальных методов является клеточный, из мультифрактальных – анализ на базе показателя Гельдера (на примере финансовых показателей компаний, действующих на российском рынке производства и обслуживания нефтегазодобывающего комплекса)
Обосновано, что персистентные временные ряды прогнозируются точнее, чем случайное блуждание	V. Kulish, V. Horák [21]	R/S-анализ	На примере ряда индекса Доу-Джонса установлено, что участки ряда с показателем Херста более 0,5 могут быть предсказаны более точно, чем участки, у которых показатель близок к 0,5; сделан вывод о том, что показатель Херста может служить мерой предсказуемости

Окончание таблицы 1

Ключевые достижения	Авторы	Подходы (методы)	Результаты
Обосновано, что фрактальные модели могут осуществлять точечные прогнозы значений котировок с более высокой точностью, чем нефрактальные	Е.С. Остапенко, Т.А. Дунаева [12]	R/S-анализ, ARFIMA-моделирование	На примере цен акций компании Google установлено, что модель ARFIMA дает более точные прогнозы, чем ARMA; сделано предположение о том, что игнорирование наличия длинной памяти приводит к большей погрешности прогноза, чем учет длинной памяти при ее отсутствии
	М.В. Прудский [10]	R/S-анализ, ARFIMA-моделирование	Сделаны выводы о том, что модель ARFIMA позволяет с более высокой точностью, чем другие модели, прогнозировать курс доллара к рублю
	И.И. Белолипцев, С.А. Фархиева [13]	Метод минимального покрытия, нейросетевое моделирование	На примере курсов акций ОАО «Татнефть» показано, что использование индекса фрактальности в качестве предиктора улучшает прогностические свойства нейросетевой модели

На наш взгляд, общим пробелом в работах о прогнозировании будущих значений курсов финансовых инструментов является то, что в них, как правило, исследован лишь один временной ряд. Кроме того, не во всех работах [10] произведено сравнение точности прогнозов фрактальных моделей и максимально похожих на них нефрактальных.

При этом необходимо отметить, что во всех исследованиях были получены положительные результаты, продемонстрировавшие эффективность фрактального подхода к анализу финансовых рынков. Как показывает обзор, в основном фрактальный подход используется авторами для подтверждения гипотезы о фракталь-ности и персистентности финансовых временных рядов, а также для исследования возможности предсказывать критические точки (кризисы). Для определения фрактальных свойств рядов чаще всего используется исторически первый и наиболее простой метод – R/S-анализ в совокупности с показателем Херста, реже применяются альтернативные методы – ДФА, клеточный, спектральный. Перспективному мультифрактальному подходу почти не уделяется внимания, несмотря на то, что, по мнению некоторых авторов [2], реальные финансовые ряды обладают спектром фрактальных показателей на разных масштабах и лучше анализируются именно методами мультифрактального анализа. По всей видимости, это связано с высокой сложностью применения таких методов. Также было обнаружено лишь небольшое количество работ, посвященных точечному прогнозированию значений финансовых временных рядов [10; 12; 13], причиной чего предположительно является скептическое отношение многих исследователей к самой возможности получения таких достаточно точных прогнозов. В рассмотренных работах наибольшей популярностью пользуются эконометрические модели с долгой памятью (в частности, ARFIMA), которые, согласно выводам авторов, обладают высокой прогностической способностью. Тем не менее применение таких моделей на российском финансовом рынке изучено недостаточно хорошо, работы и, соответственно, примеры полученных данным методом успешных предсказаний единичны, поэтому требуется дальнейшее исследование их эффективности. Не было обнаружено попыток применения для прогнозирования фрактальных расширений GARCH-моделей, в то время как теоретически они должны лучше, чем ARFIMA, описывать реальные финансовые ряды, для которых характерно явление кластеризации волатильности. Кроме того, авторам не встретилось сравнения фрактальных и нефрактальных моделей на достаточно больших массивах ценовых данных. Как правило, для исследования выбирается лишь один финансовый инстру- мент, в ряду курсов которого моделируется фиксированной участок, на основании чего делаются выводы о прогностических способностях моделей. Современные инструментальные средства и вычислительные возможности аппаратного обеспечения позволяют проводить массовое моделирование, сравнивая сотни и даже десятки тысяч моделей на множестве участков ценовых рядов. Настоящая работа не претендует на полномасштабное исследование качества различных моделей на обширном эмпирическом материале, однако, как показали его результаты, можно говорить о некоторых преимуществах фрактальных модификаций в различных условиях.

Прежде чем переходить к методике исследования, следует кратко коснуться теоретических аспектов фрактального анализа и его категориального аппарата.

Размерность - это число измерений геометрического объекта или множества. Топологической размерностью ( D T ) называют минимальное количество координат, необходимое для описания объекта. D T может принимать только целые значения, подходит для описания идеализированных, гладких множеств, таких как прямая линия, куб, сфера [17] . Но в природе такие практически не встречаются. Для описания реальных объектов подходит размерность Хаусдорфа ( D H ), являющаяся обобщением понятия топологической размерности D_T. D H идеальных объектов (гладких кривых, поверхностей) совпадает с их D T , в случае же самоподобных структур (таких, как береговая линия) D H всегда превышает D_T и является нецелой (дробной) величиной. Такая размерность показывает, насколько плотно и равномерно элементы множества заполняют пространство. Наконец, Б. Мандельбротом введен термин «фрактальная размерность» ( D ) для обозначения частного случая размерности Хаусдорфа (дробной). Множества, для которых справедливо неравенство D H > D T , Б. Мандельброт назвал фракталами. В дальнейшем в нашем исследовании термин «размерность» и обозначение D относятся именно к этому типу размерности.

Отметим, что не существует точного определения сущности категории «фрактал». Сам Б. Мандельброт охарактеризовал ее так: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому» [22] . Принято относить к фракталам объекты, обладающие следующими свойствами [10] : самоподобие или масштабная инвариантность (отдельные составляющие объекта подобны всему объекту целиком, вследствие чего при различных масштабах объект выглядит одинаково); масштабирование по степенному закону (изменение характеристик объекта с изменением масштаба рассмотрения имеет степенную зависимость); фрактальная размерность, которая превосходит топологическую (при увеличении соотношение между масштабом и каким-либо параметром фрактала постоянно и равно фрактальной размерности [2] ).

Сущность фрактального анализа как инструмента описания различных объектов заключается в том, что производится обработка масштабированием фрактальной структуры и описывается распределение какой-либо структурной характеристики (или меры) при этом масштабировании [18] . Фрактальными свойствами могут обладать не только математические абстракции и природные сущности, но и временные ряды, являющиеся численным дискретным описанием непрерывных динамических процессов. Как правило, когда говорят об анализе и прогнозировании динамики финансовых рынков, подразумевают исследование именно ценовых рядов финансовых инструментов. Если обратить внимание на графики котировок акций или валют, можно заметить их сильную изре-занность (признак фрактальной размерности), а также то, что при рассмотрении на различных временных масштабах они выглядят похоже, нельзя с уверенностью сказать, дневные это курсы, месячные или минутные (самоподобие). На свойство масштабирования по степенному закону указывает форма распределений с «толстыми хвостами».

Если для пространственной структуры основной фрактальной характеристи- кой является ее размерность, то в случае временного ряда говорят о наличии у процесса «долгой памяти», когда ему присуще свойство персистентности. Эти понятия тесно взаимосвязаны. Чтобы численно охарактеризовать свойство «долгой памяти», британским гидрологом Г. Херстом был введен показатель H, позднее названный его именем [14]. Кроме того, Н.В. Старченко был предложен оригинальный метод оценивания фрактальной размерности фи- нансовых временных рядов и введен новый показатель - индекс фрактальности (д) [8].

Финансовые временные ряды демонстрируют сложное непериодическое поведение, при котором тренды и флэты хаотическим образом сменяют случайное блуждание. Рассмотренные фрактальные показатели позволяют идентифицировать состояние процесса и делать выводы о его дальнейшем поведении. В табл. 2 приведено их сопоставление [19] .

Таблица 2

Взаимосвязь показателей фрактальности временного ряда

Показатель	Диапазон значений	Характер ряда
		Антиперсистентный (флэт)	Случайный (стохастический)	Персистентный (тренд)
Показатель Херста, H	[0; 1]	0 <  H < 0,5	H = 0,5	0,5 <  H < 1
Фрактальная размерность, D	[1; 2]	1,5 <  D < 2	D = 1,5	1 <  D < 1,5
Индекс фрактальности, д	[0; 1]	0,5 <  д < 1	д = 0,5	0 <  д < 0,5

Из таблицы 2 видно, что все три показателя согласуются друг с другом при индикации состояний хаотического процесса. В работе [19] дана следующая характеристика этих состояний:

• 1)    Тренд - персистентный участок, на котором поддерживается тенденция изменений. Если в текущем периоде показатель увеличивался, с большой долей вероятности он продолжит расти и в следующем периоде.

• 2)    Флэт - антиперсистентный участок, направление изменений на котором постоянно меняется (чаще, чем при случайном характере процесса). Такой характер динамики называют «возврат к среднему». Если в текущем периоде показатель увеличивался, с большой долей вероятности в следующем периоде направление изменения показателя сменится, в результате чего его значение не может далеко уйти от среднего.

• 3)    Случайное блуждание - промежуточное состояние между трендом и флэтом. Динамика процесса случайна, будущие значения не зависят от прошлых.

Охарактеризовав теоретические основы фрактального анализа, рассмотрим методы оценивания фрактальных характеристик финансовых рядов. Как показал обзор литературы, существует достаточно большое количество способов вычисления как фрактальной размерности, так и показателя Херста. Рассмотрим два метода, которые и будут применены в исследовании.

Метод минимального покрытия, детально разработанный Н.В. Старченко [8], позволяет характеризовать локальную динамику процесса. Для этого сужается репрезентативный масштаб до значений, при которых временной ряд не меняет своего поведения, и определяется локальная фрактальная размерность [19]. Алгоритм метода состоит из следующих шагов. Пусть процесс характеризуется некоторой функцией у = f(t) на отрезке [ а = t0 < < t1 < ••• < tm = b], i = 1, 2, ..., m. Отрезок [a, b] разбивается на m сегментов равной длины 8 = ^^ = ti — ti-1. Затем график функции покрывается прямоугольниками с основанием 8 таким образом, чтобы это покрытие было минимальным по площади. Тогда высота прямоугольника на отрезке [ti-1, ti] будет соответствовать амплитуде Ai (8), равной разности максимального и минимального значения f( t) на данном отрезке. Накопленная амплитуда на всем отрезке вычисляется как Vf(8) = = Sm=i А($), а площадь минимального покрытия как 5^(8) = V^(8)8. Очевидно, что при сокращении длины отрезка 8 точность вычисления площади покрытия будет увеличиваться. Имеет место степенная зависимость Sfl(8)~82-D при 3 ^ 0, где D - фрактальная размерность. Из этой формулы следует, что V^(8)~8-^ при 3^0, где ^ = D^ — 1. Н. В. Старченко назвал показатель D^ размерностью минимального покрытия, а µ – индексом фрактальности. Показатель µ вычисляют как взятый с отрицательным знаком коэффициент при независимой переменной в уравнении линейной регрессии lnV^ (8) = —ц 1п8 + Ь, где b – свободный член. Показано, что для приемлемо точного определения размерности минимального покрытия достаточно репрезентативных интервалов длиной 32 и иногда даже 16 дней.

Метод нормированного размаха, или R/S-анализ (Rescaled range analysis), предложен Г. Херстом в 50-х гг. XX в. и до сих пор является одним из наиболее популярных подходов в исследованиях фрактальных рядов самой различной природы, что подтверждается обзором научных работ. Можно сказать, что для вычисления H он является «родным» методом, и некоторые авторы, говоря о показателе Херста, подразумевают его оценивание именно посредством метода нормированного размаха [3; 21]. Идея R/S-анализа состоит в том, что существует степенная зависимость вида ~~с ■ 8Н, где R - размах вариации (под вариацией показателя понимается накопленное отклонение его от среднего значения), S – стандартное отклонение показателя, δ – количество значений показателя в группе, c – некоторая константа. Вычисляемая статистика R/S является размахом, нормированным стандартным отклонением, что и дало название методу. В работе [3] подробно описан его алгоритм. Пусть дан временной ряд x(t) длиной n+1. Прежде всего его приводят к так называемым «логарифмическим доходностям» y(t) по формуле y(t) = ln-^-. Далее работают с xt-i преобразованными данными. Ряд y(t) длиной n делится на m групп значений по δ элементов. Для каждой i-й группы (i=1, 2, …, m) рассчитываются: среднее значение yi; накопленные отклонения от среднего Yt = Yt=i(yt - У) образуя m рядов Yi (t); размах Rj = max^YO) — —min(Yi(t)); стандартное отклонение

^Si = ^^^ ^^^ (у^-^ ² ;

R/S- статистика

(нормированный размах) по формуле

Rj/Sj. После полученные m величин R/S усредняются, и получается двойка элементов < R/S(S),8 >. Такие вычисления проводят для различных значений δ. Показатель Херста H определяется как коэффициент при независимой переменной в уравнении линейной регрессии ln^(8) = = Н ln 8 + с, где с - свободный член. Стоит отметить, что величина δ не может принимать значения, меньшие 10. При этом очевидно, что она является собственным делителем количества элементов в ряду n, поэтому выборку нужно формировать таким образом, чтобы максимизировать число собственных делителей – это положи- тельно скажется на точности вычисления H. Кроме того, для достижения приемлемой точности значение n должно быть достаточно высоко (несколько тысяч) [9]. В работе [17] показано, что на интервалах порядка нескольких десятков значений оценивание H не имеет смысла, так как функция R/S(δ) имеет медленный выход на асимптотический режим.

Фрактальную размерность можно вычислить через показатель Херста по формуле D=2 – H [17] .

Далее, основываясь на методологии фрактального анализа, охарактеризуем ме- тодику исследования.

Методика исследования

Для моделирования динамики курсов финансовых инструментов нами были выбраны две популярные эконометрические модели – ARIMA и GARCH – и их фрактальные модификации ARFIMA и ARFIMA-GARCH.

ARIMA (p, d, q). Интегрированная модель авторегрессии – скользящего среднего порядков p, d, q – относится к линейным моделям и предназначена для описания нестационарных процессов. Данная модель предложена Дж. Боксом и Г. Дженкинсом [23]. Ее уравнение имеет следующий вид: Ф(L)(1 — L)dXt = / + 0(L)st, где Xt - исследуемый процесс (временной ряд), L - оператор сдвига, Ф(L) - полином степени p от L, 0(L) - полином степени q от L, d – порядок интегрирования процесса Xt. Параметры p, d, q могут принимать целые неотрицательные значения.

ARFIMA ( p , d , q ). Дробно-интегрированная модель авторегрессии – скользящего среднего порядков p , d , q – является обобщением модели ARIMA ( p , d , q ), допускающим дробное значение параметра d . Предложена Дж. Хоскингом [24] . Уравнение для этой модели остается неизменным, а оператор дробного дифференцирования аппроксимируется следующим рядом: ат yd v’oo      r⁽k-d⁾

— L)u = X^n ———---L’, где Г - гам- k~0 r(-d)F(fc+1)   ’ д ма-функция [11]. Забегая вперед, отметим, что для программной реализации алгоритма моделирования ARFIMA нами была использована следующая формула вычисления ряда дробных разностей Yt: Yt = Xt + + Хк=1(—1)кП[=1(^, ~*t-k [25]- Каждая разность аппроксимируется предыдущими значениями исходного ряда, при этом «глубину» памяти, т. е. количество участвующих в вычислении значений, можно ограничить. В этой особенности проявляется учет моделью свойства «долгой памяти» процесса. Для оценки параметра d существуют специализированные методы [14], а также его можно вывести через соотношение с показателем Херста: d = Н — 0,5 [9].

GARCH (p, q). Обобщенная авторегрессионная условная гетероскедастич-ность порядков p, q являет собой семейство нелинейных моделей, предназначенных для изучения волатильности в ценовых рядах и позволяющих учитывать такие ее свойства, как кластеризация («группирование» периодов с высокой и низкой волатильностью), а также так называемый эффект «рычага» – уменьшение волатильности при росте цены, и наоборот. Классическая модификация, называемая иногда SGARCH, предложена Т. Боллерслевом [26]. Стандартно для моделей GARCH определяется два уравнения – условного математического ожидания доходности yt и условной дисперсии at [27]. Формула классической модели имеет следующий вид: ot = «о + Sf=i «I • У2-1 + Х“м fy • at-j. Для корректного определения условной дисперсии должны выполняться ограничения а0 > 0, ai > 0, ^j > 0. В этой модели ряд    у2    удовлетворяет процессу

ARMA (max [p , q ], q ) модели. Величина a t служит условной дисперсией процесса y_t\Y_t-1~^(0, a 2 ). На практике часто используется модель GARCH (1, 1) [28] .

ARFIMA-GARCH ( p , d , q ). Данная модель является модификацией SGARCH-модели, в которой в качестве уравнения условного математического ожидания выступает не ARMA, а ARFIMA [29] . Таким образом, учитываются фрактальные свойства моделируемого процесса.

В процессе исследования предполагается проверить ряд гипотез, высказанных авторами научных работ по данной тематике, а также выдвинутых авторами настоящей статьи:

• 1)    Учет моделями фрактальных свойств моделируемых процессов позволяет повысить точность прогнозов [10] .

• 2)    Финансовые временные ряды обладают переменной структурой, их фрактальные свойства на различных участках различны [19; 30] .

• 3)    Использование локальных показателей фрактальности (оцененных на моделируемом участке ряда) вместо глобальных (оцененных по всему ряду) для вычисления параметра дробного дифференцирования положительно сказывается на точности прогнозов [7] .

• 4)    Учет при моделировании «долгой памяти» процесса в том случае, если в действительности он ею не обладает, не ухудшает качества прогнозов, в то время как непринятие во внимание данной особенности процесса при ее наличии снижает их точность [12] .

• 5)    При росте длины прогноза его точность снижается.

• 6)    При переходе к лог-доходностям фрактальные свойства ряда меняются.

Для проверки перечисленных гипотез в качестве исходных данных для моделирования следует взять ценовые ряды различных финансовых инструментов с достаточно длительной предысторией (несколько тысяч значений). Предполагается выполнить преобразование цен yt к логарифмическим доходностям по формуле хк = = 1п-^~ [3] и далее моделировать эти до-yt-i ходности. Так как предположительно ценовые ряды обладают переменной фрактальной структурой, влияющей на качество моделирования и прогнозирования, не следует аппроксимировать модели на всей истории рядов, необходимо выбрать относительно короткий локальный участок. В то же время проблема определения границ таких участков остается актуальной, в литературе не было обнаружено соответствующей методики. Было решено применить так называемый метод «скользящего окна» (sliding window) [31] и рассмотреть все возможные локальные участки рядов с их начала до конца с шагом 1, на каждом попытаться аппроксимировать модели и проверить их прогнозирующую способность.

В машинном обучении существует задача выявления «эффекта от воздействия» (treatment effect) [32]. Типичный пример ее решения – определение эффективности лекарственных препаратов. Идея метода заключается в том, чтобы оказать на объект некоторое воздействие, оценить изменение его состояния, затем не оказывать воздействий и вновь оценить изменение состояния. Разница между изменениями и будет предполагаемым эффектом от воздействия. В идеале воздействовать и не воздействовать нужно на один и тот же объект одновременно. В жизни реализовать это затруднительно, однако при анализе ретроспективных ценовых данных такой подход становится возможным. Поэтому в исследовании решено применить данную концепцию при сравнении моделей. В качестве воздействия будет выступать учет моделями свойств долгой памяти процессов. Для этого следует тестировать модели в максимально похожих условиях, т. е. на одних и тех же данных. Причем обе

ARMA-модели (фрактальная и обычная) должны пройти проверки на адекватность: оценки коэффициентов должны быть статистически значимы (так как не всегда наилучшая аппроксимированная к данным модель обладает только значимыми коэффициентами, решено принимать модели, у которых их более 50%); в остатках должна отсутствовать автокорреляция (проверка тестом Льюнга – Бокса); остатки должны быть распределены по нормальному закону (проверка тестом Лиллиефорса) [28] . Кроме того, отбрасываются модели «белого шума» ARMA (0, 0) и «случайного блуждания» ARIMA (0, 1, 0), т. е. модели, сумма порядков p , q которых меньше 1. В качестве показателя точности прогнозирования решено применять среднюю абсолютную ошибку МАЕ = 1 I [ ₌ i ly_t - y_t|, где y_t - фактическое значение наблюдения, y_t - прогнозное значение наблюдения, T – длина тестового участка. В качестве локальной фрактальной характеристики рядов решено использовать размерность минимального покрытия D ^ , вычисляемую методом минимального покрытия. Данный метод выбран потому, что позволяет оценивать размерность на небольшом количестве наблюдений (от 16) с приемлемой точностью [17] . В качестве глобальной фрактальной характеристики (оцениваемой по всей длине ряда) выбран показатель Херста H , вычисляемый методом R/S-анализа. Конкретных рекомендаций по величине участка аппроксимации (длине скользящего окна) в литературе обнаружено не было, поэтому он составляет 128 наблюдений, такое значение близко к круглому значению 100 и при этом является степенью двойки (как того требует специфика метода минимального покрытия). Предполагается делать краткосрочные прогнозы глубиной 1, 3 и 10 шагов. Величины MAE, полученные за один проход по ряду, усредняются по каждой из моделей, такие средние значения предполагается сравнивать между собой.

Программную реализацию методики решено осуществлять на языке программирования R в среде разработки RStudio. Для вычисления показателя Херста, реализации процедур дробного дифференцирования и метода минимального покрытия были написаны пользовательские функции в со- ответствии с приведенными в литературе алгоритмами. Аппроксимация моделей ARIMA и ARFIMA выполняется с использованием готовой функции auto.arima() из пакета forecast. Данная функция отбирает из нескольких конкурирующих моделей наилучшую по информационному критерию AIC. Аппроксимация моделей GARCH осуществляется через функции ugarchspec() (задание спецификации модели) и ugarchfit() (непосредственная идентификация параметров модели) из пакета rugarch. Использована базовая модификация SGARCH. При обучении модели ARFIMA-GARCH процедуру вычисления дробных разностей, как и оценивание величины d, решено доверить встроенным в пакет rugarch-алгоритмам.

Далее выполняется сравнение четырех авторегрессионных моделей: ARIMA (p,d,q); ARFIMA (p,d,q) (параметр d вычислен через локальную размерность D^, оцененную по исходному ряду котировок); ARFIMA (p,d,q) (параметр d вычислен через локальную размерность D^, оцененную по ряду лог-доходностей); ARFIMA (p,d,q) (параметр d вычислен через глобальный показатель Херста H, оцененный по всему ряду). Параметры p, q всех моделей оценены по ряду наблюдений.

Выполняется сравнение двух GARCH (1,1)-моделей: SGARCH (модель условного математического ожидания – ARMA); ARFIMA-GARCH (модель условного математического ожидания – ARFIMA).

Прежде чем переходить непосред- ственно к моделированию и прогнозированию в соответствии с составленной методикой необходимо проанализировать входные данные.

Данные

В качестве моделируемых ценовых рядов выбраны котировки набора финансовых инструментов, на котором проводилось исследование в работе [10]. В набор дан- ных внесены следующие изменения: исключены акции компании «Газпром» и биржевой индекс RTSI, добавлены валютные пары USDRUB и EURRUB (табл. 3). Использованы дневные цены закрытия.

Таблица 3

Исследуемые финансовые инструменты и индекс

№ п/п	Тикер	История	Количество наблюдений
1	ALRS	11.29.2011 – 02.05.2018	1616
2	EURRUB	01.01.2000 – 29.04.2018	4637
3	GMKN	31.01.2001 – 02.05.2018	4118
4	MTSS	15.10.2003 – 02.05.2018	3614
5	ROSN	19.07.2006 – 02.05.2018	2948
6	USDRUB	01.01.2000 – 29.04.2018	4867
7	VTBR	28.05.2007 – 02.05.2018	2736
8	IMOEX	05.01.2000 – 02.05.2018	4574
9	LKOH	05.01.2000 – 02.05.2018	4575
10	SBER	05.01.2000 – 02.05.2018	4563

Источник:  ФИНАМ. URL: https://www.

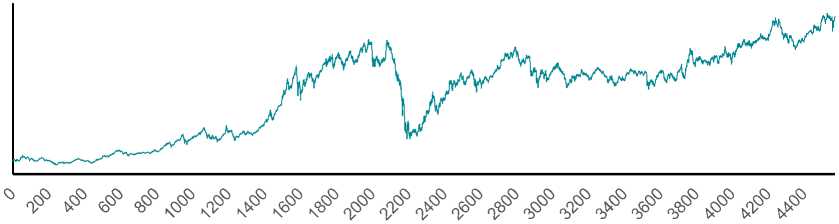
На рис. 1–4 приведена динамика показателей ряда на примере индекса ММВБ как индикатора состояния российского финансового рынка (характеристики других инструментов сопоставимы).

Эмпирический показатель Херста H для исходных уровней ряда составил ровно 1 с R²=0,9996, т. е. динамика IMOEX на протяжении без малого 20 лет имеет выраженный тренд, что заметно по графику. Динамика локальной размерности колеблется в диапазоне (1,05; 1,5), что, во-первых, подтверждает наличие у процесса долгой памяти, а во-вторых, укладывается в рамки гипотезы о переменной структуре исходных уровней ряда (размерность меняется в широких диапазонах).

Эмпирический показатель Херста H для лог-доходностей равен 0,5341 с R2=0,9965, что говорит о слабо выраженной персистентности процесса. При этом график лог-доходностей визуально напомина- ет «белый шум» с нулевым средним, но локальные размерности в основном находятся в диапазоне (1,5; 1,75), т. е. флэта. Поэтому в данном случае глобальные и усредненные локальные фрактальные характеристики не согласуются. Наличие таких особенностей вызвало вопросы о способе расчета параметра d модели ARFIMA: стоит ли оценивать его по моделируемому ряду, демонстрирующему устойчивую антиперси- стентность, либо по трендовому ряду исходных уровней.

Коэффициент эксцесса распределения лог-доходностей индекса ММВБ равен 15,3592, коэффициент симметрии –0,2405. Это свидетельствует о том, что распределение не соответствует нормальному, характеризуется вытянутым пиком и «толстыми хвостами», как и ожидалось (для нормального распределения значения коэффициентов составляют соответственно 3 и 0).

Значения индекса

Отсчеты

Рис. 1. Значения индекса ММВБ

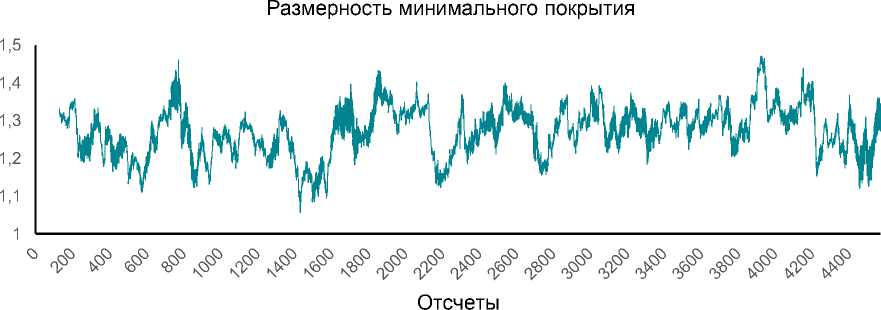
Рис. 2. Динамика фрактальной размерности значений индекса ММВБ

Лог-доходности индекса

0,3

0,2

0,1

-0,1

-0,2

-0,3

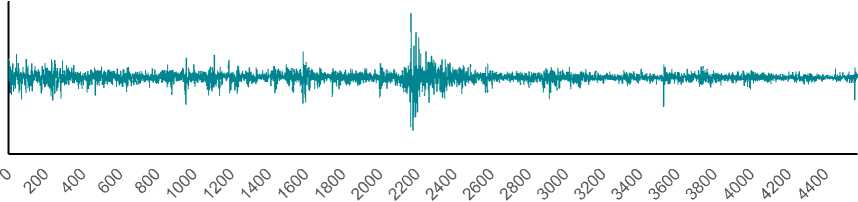
Отсчеты

Рис. 3. Лог-доходности индекса ММВБ

Размерность минимального покрытия

1,8

1,7

1,6

1,5

1,4

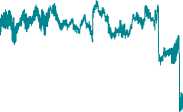
1,3

^ ^ tS^ ^ %°° ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ с^ ^ ^ ^ ^ ^

Отсчеты

Рис. 4. Динамика фрактальной размерности лог-доходности индекса ММВБ

В следующем разделе статьи описаны и проанализированы полученные в ходе моделирования результаты.

Результаты и их обсуждение

Р езультаты моделирования и прогнозирования представлены в табл. 4–6.

Усредненные показатели MAE при глубине прогноза 1 шаг вперед *

Таблица 4

Тикер	ARIMA	ARFIMA ( D µ )	ARFIMA ( D µ -log)	ARFIMA ( H )	ARIMA-GARCH	ARFIMA-GARCH
ALRS	0,01922**	0,01888	0,01866	0,01826*	0,01949*	0,02044
EURRUB	0,00693**	0,00681	0,00659*	0,00677	0,00509*	0,00516
GMKN	0,01424	0,01395*	0,01408	0,01442**	0,01563	0,01534*
MTSS	0,01454	0,01472	0,01393*	0,01455**	0,01699	0,01678*
ROSN	0,01982	0,02084**	0,01898	0,01816*	0,01664	0,01636*
USDRUB	0,00536	0,00508*	0,00556**	0,00547	0,00588*	0,00595
VTBR	0,01522	0,01504	0,01433*	0,01530**	0,02363	0,02198*
IMOEX	0,01285**	0,01284	0,01270	0,01261*	0,01382	0,01342*
LKOH	0,01608**	0,01561*	0,01575	0,01598	0,01668	0,01602*
SBER	0,01590	0,01531*	0,01591**	0,01551	0,01734	0,01694*
Среднее	0,01401**	0,01391	0,01365*	0,01370	0,01512	0,01484*

* В табл. 4–6 звездочкой (*) обозначен лучший прогноз в своем классе моделей, двумя звездочками (**) –

худший прогноз.

Таблица 5

Усредненные п оказатели M AE при глубине прогноза 3 шага впер ед

Тикер	ARIMA	ARFIMA ( D µ )	ARFIMA ( D µ -log)	ARFIMA ( H )	ARIMA-GARCH	ARFIMA-GARCH
ALRS	0,01770	0,01784**	0,01749	0,01723*	0,01809*	0,01892
EURRUB	0,00598	0,00621**	0,00585*	0,00602	0,00508	0,00506*
GMKN	0,01452	0,01446	0,01409*	0,01462**	0,01606*	0,01607
MTSS	0,01516	0,01535	0,01468*	0,01536**	0,01837*	0,01859
ROSN	0,02179	0,02222**	0,02096	0,02055*	0,01781	0,01760*
USDRUB	0,00576	0,00571*	0,00585	0,00598**	0,00587	0,00579*
VTBR	0,01158	0,01127*	0,01128	0,01165**	0,02233	0,02172*
IMOEX	0,01212	0,01218**	0,01206	0,01202*	0,01380	0,01345*
LKOH	0,01679**	0,01675	0,01652*	0,01675	0,01732	0,01679*
SBER	0,01512	0,01455*	0,01524**	0,01489	0,01745	0,01707*
Среднее	0,01365	0,01365**	0,01340*	0,01351	0,01522	0,01511*

Таблица 6

Усредненные показатели MAE при глубине прогноза 10 шагов вперед

Тикер	ARIMA	ARFIMA ( D µ )	ARFIMA ( D µ -log)	ARFIMA ( H )	ARIMA-GARCH	ARFIMA-GARCH
ALRS	0,01443**	0,01401	0,01411	0,01383*	0,01765*	0,01793
EURRUB	0,00639*	0,00646	0,00647	0,00648**	0,00483*	0,00484
GMKN	0,01531**	0,01514	0,01495*	0,01527	0,01564*	0,01595
MTSS	0,01297	0,01310**	0,01275*	0,01308	0,01563*	0,01566
ROSN	0,01817	0,01818**	0,01771	0,01752*	0,01730	0,01711*
USDRUB	0,00544	0,00549	0,00542*	0,00557**	0,00590	0,00582*
VTBR	0,01261	0,01242*	0,01256	0,01268**	0,02834	0,02810*
IMOEX	0,01224	0,01225**	0,01217*	0,01219	0,01453	0,01430*
LKOH	0,01683**	0,01678	0,01678*	0,01679	0,01763	0,01733*
SBER	0,01639	0,01590*	0,01639**	0,01630	0,01850	0,01804*
Среднее	0,01308**	0,01297	0,01293*	0,01297	0,01559	0,01551*

По результатам проведенного исследования можно сделать следующие выводы.

• 1)    Основная гипотеза исследования о лучшей прогностической способности фрактальных эконометрических моделей в сравнении с классическими не отвергается. Во всех, за исключением одного, случаях различные вариации ARFIMA оказались точнее, чем ARIMA. В большинстве случаев ARFIMA-GARCH также оказались точнее, чем SGARCH.

• 2)    Гипотеза о переменной фрактальной структуре финансовых временных рядов подтверждается, что доказывают изменчивые графики локальных размерностей (амплитуда колебаний составляет 0,4– 0,5). Это закономерно и объясняется неоднородностью рыночной динамики курсов финансовых инструментов, ее хаотичностью, наличием в рядах участков как с ярко выраженным трендом, так и со случайным блужданием, наличием эффекта кластеризации волатильности. В то же время возникает задача кластеризации участков ряда с различной фрактальной размерностью. Методики ее решения в литературе обнаружено не было, однако успешная работа в этом направлении позволила бы определять, в каком состоянии процесс находится в настоящий момент, что расширило бы возможности для предсказания его будущего поведения. Кроме того, знание таких участков позволит выявить условия применимости различных моделей.

• 3)    Гипотеза о том, что использование локальных показателей фрактальности вместо глобальных для вычисления пара-

• метра дробного дифференцирования увеличивает точность прогнозов, не подтверждается. В среднем модель с глобально оцененным параметром d показала незначительно меньшую точность, чем с локальными. Предположительно это можно объяснить следующими ограничениями примененного инструментария. Во-первых, моделируемые локальные участки выбирались грубо, методом «скользящего окна» фиксированного размера. Разумно предположить, что несколько раз это окно совпало с границами истинного участка с концентрированным однотипным поведением процесса и оцененная величина его размерности также являлась истинной. Не исключено, что среди фрактальных моделей, аппроксимированных на таких участках, наибольшей точностью прогнозов обладали те, параметр d которых определялся по локальной размерности. Однако проверить это невозможно, так как ошибка прогнозов усреднялась и итоговая анализируемая величина MAE учитывает как прогнозы, полученные на истинных участках, так и прогнозы на участках, содержащих границы состояния процесса (например, тренда и случайного блуждания), а оцененная на таких «смешанных» участках величина локальной размерности адекватно описывает этот участок не в большей степени, чем величина глобальной. Во-вторых, для оценки локальной и глобальной размерностей и, следовательно, параметра d моделей были использованы разные методы (соответственно метод минимального покрытия и R/S-анализ). Данные ограничения методики

создают предпосылки для дальнейших исследований и проверок гипотезы о преимуществе применения локальных размерностей для целей прогнозирования.

• 4)    Гипотеза о том, что учет несуществующего эффекта долгой памяти не ухудшает прогнозов, а его игнорирование существующего – ухудшает, не отвергается. Модель с короткой памятью ARIMA показала самые низкие результаты среди авторегрессионных моделей почти в каждом случае. Чтобы получить более убедительные доказательства данного утверждения, следует провести исследование с акцентом на сравнении фрактальных и нефрактальных моделей на выявленных участках с долгой памятью, а также на участках без нее. Потенциальным результатом такого исследования может стать рекомендация всегда использовать модели ARFIMA вместо ARIMA.

• 5)    Гипотеза о том, что при росте длины прогноза его точность снижается, не подтверждается. На горизонтах прогнозирования 1, 3, 10 шагов точность остается сопоставимой. По нашему мнению, причины несогласованности результатов с этой достаточно очевидной гипотезой (проще предсказать одно ближайшее значение, чем серию, вероятность реализации такого прогноза выше) – в следующем ограничении методики: для оценки точности прогноза использовалась усредненная абсолютная величина ошибки, не учитывающая направления ошибок единичных. Возможно, с ростом глубины прогноза модели ошибаются чаще именно в направлениях динамики курсов финансовых инструментов. Поэтому данный момент требует дальнейших исследований.

• 6)    Гипотеза об изменении фрактальных свойств при переходе к лог-доходностям подтверждается, о чем свидетельствуют различные значения показателя Херста, а также графики локальных размерностей до и после этой операции. Данный факт объясняется тем, что лог-трансформация, как и дифференцирование, устраняет в ряду тренд, поведение ряда начинает напоминать паттерн «возврат к среднему».

• 7)    В сравнении ARIMA и GARCH-моделей превосходство в точности прогнозирования осталось за ARIMA. Причиной этого может быть то, что исследуемые ценовые ряды не обладают высокой волатильностью, для них нехарактерен эффект ее кластеризации, поэтому GARCH-модели не демонстрируют преимуществ. Однако исследование этих моментов (в частности, тестов на условную гетероскедастичность в остатках ARMA-моделей) не проводилось.

• 8)    В среднем небольшое преимущество перед другими получила модель ARFIMA с параметром d , вычисленным по антиперсистентному ряду лог-доходностей, а не по трендовому исходному ряду котировок. Этот факт не укладывается в рамки гипотезы о том, что участки с долгой памятью лучше моделируются [21] . Предполагаемым объяснением данного факта может послужить то, что, как подтвердили результаты исследования, при лог-трансформации ряда меняются его фрактальные свойства, в том числе и величина размерности, из которой выводится значение d . Логичным выглядит то, что учитываться при моделировании должны фрактальные свойства непосредственно моделируемого ряда. Данный ряд имеет преимущественно антиперси-стентный характер, практически не обладает долгой памятью, и вопрос о том, насколько вообще к нему применимы модели, ее учитывающие, остается открытым. Этот момент требует дальнейших исследований.

Таким образом, можно констатировать, что полученные в результате исследования факты согласуются с четырьмя из проверяемых гипотез и противоречат двум из них. При этом причиной того, что эти гипотезы не подтвердились, предположительно стали ограничения методики, поэтому отбрасывать их нельзя, необходимы дальнейшие исследования в данном направлении.

Заключение

Основная выдвинутая авторами гипотеза о том, что при прогнозировании финансовых временных рядов фрактальные модели позволяют получать более точные прогно- зы, чем нефрактальные, не противоречит данным исследования. Также было подтверждено, что:

• 1)    Финансовые ряды имеют изменчивую фрактальную структуру, величина их локальной фрактальной размерности зависит от границ рассматриваемого участка.

• 2)    Модели с долгой памятью показывают устойчивое преимущество перед моделями с короткой памятью на подавляющем большинстве данных.

• 3)    При трансформации исходного ряда курсов финансовых инструментов его фрактальные свойства меняются.

Все эти факты согласуются с положениями теории о фрактальности финансовых рынков и результатами других исследований. Новизной исследования является то, что авторами впервые получено подтверждение этих гипотез на большом массиве данных, а также поставлена и решена проблема кластеризации участков финансовых рядов с различными фрактальными свойствами, определено, по какому ряду следует оценивать фрактальную размерность для вычисления оператора дробного дифференцирования модели ARFIMA – исходному или преобразованному (моделируемому). Это позволяет лучше определять условия применимости фрактальных эконометрических моделей и в целом развивает методологию прогнозирования динамики финансовых временных рядов, увеличивая точность прогнозов.

В ходе исследования не удалось подтвердить следующие гипотезы:

• 1)    Применение локальных показателей фрактальности вместо глобальных

для вычисления параметра дробного дифференцирования модели ARFIMA увеличивает точность прогнозов.

• 2)    С увеличением глубины прогноза его точность снижается.

• 3)    Участки рядов с долгой памятью (тренды) лучше моделируются и прогнозируются. Авторами не ставилась задача проверки данной гипотезы, однако некоторые исследователи [21] ее выдвигали.

Предположительно причиной несоответствия установленных фактов этим гипотезам явились ограничения примененного авторами методического инструментария, поэтому результаты настоящего исследования не являются достаточным основанием для того, чтобы данные гипотезы отвергнуть как ошибочные.

На основании анализа полученных результатов перспективными направлениями исследований являются: разработка метода определения границ локальных участков финансовых рядов с разными фрактальными свойствами; формулирование рекомендаций относительно того, по какому ряду (исходному или преобразованному) следует оценивать оператор дробного дифференцирования модели ARFIMA; проверка гипотезы о преимуществе применения локальных размерностей для целей прогнозирования, влиянии длины прогноза на его точность и о лучшей прогнозируемости рядов финансовых инструментов на их трендовых участках, исследование различных фрактальных модификаций GARCH-моделей (FIGARCH, FIAPARCH и др.) и выявление условий их применимости.