Моделирование и прогнозирование государственного долга в Южной Африке

Автор: Мосикари Т.

Журнал: Экономические и социальные перемены: факты, тенденции, прогноз @volnc-esc

Статья в выпуске: 1 т.17, 2024 года.

Бесплатный доступ

Основным интересом любой развивающейся страны является сохранение оптимального уровня государственного долга. В настоящее время правительства развивающихся стран крайне обеспокоены по поводу важности госдолга для определения пути развития и роста. Цель исследования состоит в моделировании и прогнозировании размера общего государственного долга Южной Африки, где со времен финансового кризиса 2008 года показатели существенно выросли и до сих пор не вернулись к прежним значениям. Государственный долг представляет собой важнейший инструмент для малого и среднего бизнеса в экономике Южной Африки, ключевой источник фискальной политики. В ходе работы использовалась модель Бокса - Дженкинса (ARIMA). Как правило, при моделировании временных рядов в первую очередь необходимо оценить порядок интегрирования каждого ряда. Авторами был проведен тест Дики - Фуллера (ADF) для анализа единичных корней. Второй шаг заключался в выборе наиболее подходящей модели прогнозирования государственного долга. С помощью информационного критерия Акаике (AIC) в соответствии со значимостью коэффициента из конкурирующих моделей была выбрана модель ARIMA 13,1,1. Согласно прогнозу, ожидается сокращение объема государственного долга. В работе показана важность проведения жесткой налогово-бюджетной реформы для того, чтобы свести государственный долг к минимуму.

Еще

Государственный долг, модель arima, прогноз, южная африка

Короткий адрес: https://sciup.org/147243372

IDR: 147243372 | DOI: 10.15838/esc.2024.1.91.13

Текст научной статьи Моделирование и прогнозирование государственного долга в Южной Африке

Успех бизнеса, государственной инвестиционной и макроэкономической политики зависит от точности прогнозирования размера государственного долга, который также называют правительственной задолженностью, поскольку он включает общую сумму обязательств правительства страны. Чаще всего он рассматривается как доля валового внутреннего продукта (ВВП). Государственный долг является важнейшим источником ресурсов правительства для финансирования государственных расходов и заполнения пробелов в бюджете, поэтому в отношении к ВВП обычно используется в качестве показателя способности правительства выполнять свои обязательства в будущем. Согласно (Burriel et al. 2020), государственный долг представляется неотъемлемой частью функционирования рыночной экономики. В литературе говорится о том, что для любой экономики существуют определенные издержки и выгоды, связанные с долгом. Преимуществом в первую очередь является важная роль госдолга в функционировании финансовой системы и проведении денежно-кредитной политики. Во-вторых, государственный долг может оказывать прямое воздействие на благосостояние населения до тех пор, пока выступа- ет надежным активом для страхования против кумулятивных рисков. С другой стороны, высокий уровень долговой нагрузки в конечном счете может препятствовать долгосрочному росту. Это возможно в том случае, когда заемные средства привлекаются для финансирования непроизводительных расходов или превышают оптимальный уровень государственного капитала (Checherita-Westphal et al., 2014).

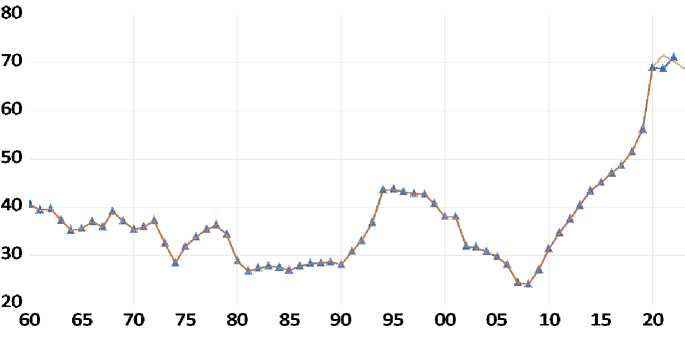
По данным, представленным в (Were, Mollel, 2020), средний уровень государственного долга в странах Африки, расположенных к югу от Сахары (SSA), превысил 50% от ВВП по состоянию на конец 2017 года. Финансовый кризис середины 2008 года привел к резкому росту государственного долга во многих развивающихся странах и странах с развитой экономикой (Cecchetti et al., 2010). В исследовании (Balassone et al., 2011) причинами этого названы растущий государственный долг в экономике, отсутствие накопленных сбережений и низкий уровень инвестиций. Кроме того, в Южной Африке финансовая неустойчивость госучреждений привела к увеличению государственного долга, которое наблюдается уже на протяжении многих лет (Schularick, 2012). На рисунке 1 представлено отношение общего государственного долга к ВВП в период с 1960 по 2022 год.

Рис. 1. Доля общего государственного долга от ВВП за 1960–2022 гг., %

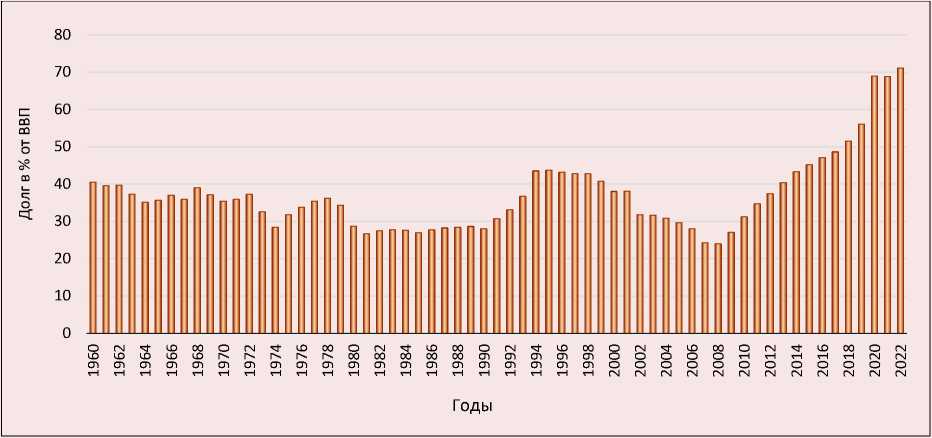
Источник: расчеты авторов по данным ЮАРБ (SARB).

Согласно представленным данным, изменение доли общего государственного долга от ВВП в период с 1960 по 1978 год отличается циклическим характером, во время цикла максимальное значение составило 40%, минимальное – 28,4%. Период с 1980 по 1990 год характеризуется самыми низкими значениями госдолга – в среднем около 29,3% от ВВП. В 1998 году общий долг составлял 42,7% от ВВП, в 2008 году показатели значительно снизились до 24% от ВВП. По данным (Mahadea, 1998), наблюдаемое сокращение государственного долга было достигнуто за счет проведения успешной политики экономического роста, занятости и перераспределения (GEAR). Однако в период с 2008 по 2022 год доля государственного долга от ВВП начала увеличиваться в геометрической прогрессии: с 24 до 71,1% соответственно. Тенденция роста государственного долга вызывает опасения, поскольку также возникает дефицит государственных финансов.

Цель исследования – определить направления решения вопроса о моделировании и прогнозировании государственного долга в Южной Африке с помощью ARIMA-моделирования. В источниках (Zhuravka et al., 2019; Munir, Mehmood, 2018) отмечается несколько факторов, которые можно использовать для описания динамики государственного долга. Однако стоит учитывать, что такой подход может вызывать трудности при выборе неподходящих и незначительных переменных при моделировании государственного долга. Поэтому в интересах настоящего исследования считаем целесообразным принять наиболее надежный метод одномерных временных рядов, такой как ARIMA.

Государственный долг — один из важнейших компонентов налогово-бюджетной политики, способствующий развитию экономики, однако его рост остается серьезной проблемой в Южной Африке. Ситуация усугубляется более быстрыми темпами его накопления по сравнению с его более медленной выплатой. Для любой экономики, в частности для такой развивающейся страны, как ЮАР, прогнозирование государственного долга имеет ключевое значение для эффективного управления. Стоит отметить, что точное и тщательное моделирование и прогнозирование государственного долга в Южной Африке, безусловно, необходимо для того, чтобы избежать неустойчивой долговой ситуации. Таким образом, в рамках статьи поставлены следующие цели: 1) проанализировать тенденции развития государственного долга в Южной Африке за рассматриваемый период; 2) разработать надежную модель прогнозирования государственного долга для Южной Африки на основе метода Бокса – Дженкинса; 3) спрогнозировать государственный долг Южной Африки за период 2021–2023 гг.

Обзор литературы

Рост государственного долга является одной из проблемных макроэкономических переменных, которые занимают центральное место в управлении государственным долгом большинства стран. Это связано с тем, что чаще всего он используется в качестве одного из фискальных показателей финансов страны. По мнению (Mellet, 2014), одним из главных инструментов фискальной политики является бюджет как средство изменения любого из фискальных элементов, позволяющий изменить покупательную способность жителей страны. В работе (Cecchetti et al., 2010) авторами показано, что при наличии высокого уровня государственного долга у страны вероятность того, что тот или иной шок вызовет нестабильную динамику долга, возрастает. Риск увеличивается, когда показатели государственного долга уже находятся на крутой восходящей траектории, что в настоящее время наблюдается в нескольких странах. Один из аргументов, приводимых российскими исследователями (Minakir, Leonov, 2019), заключается в том, что большая часть государственного долга приходится на реализацию социального обеспечения в противовес инвестиционной деятельности. Работа (Dumitrescua, 2014) послужила основой для анализа увеличения доли государственного долга в ВВП в Румынии в период 2002–2012 гг. Показано, что ситуация в стране благоприятная, прогнозируемый уровень госдолга на конец 2013 года составил 37,8% от ВВП. В работе (Nikoloski, Nedanovski, 2017) изучена динамика государственного долга Республики Македония и возможность его прогнозирования в ближайшем будущем. Учитывая современное состояние и влияние ряда политических и социально-экономических факторов в стране, было установлено, что объем государственного долга в 2017 году составил примерно 40% от ВВП.

Zaja, Krzic и Habek (Zaja et al., 2018) провели исследование по прогнозированию финансовых переменных в экономиках отдельных европейских стран (Португалия, Ирландия, Греция, Испания и Республика Хорватия) с использованием метода наименьшего абсолютного отклонения (LAD). На основе анализа фискальных переменных между странами можно отметить истощение сбалансированных бюджетов и преобладание государственного долга. В статье (Zhuravka et al., 2019) были исследованы теоретические и практические аспекты прогнозирования государственного долга в Украине. Сделан вывод о том, что модель ARIMA (1,1,3) наилучшим образом описывает тенденцию динамики государственного долга и обеспечивает наибольшую точность для дальнейшего прогнозирования. В ходе анализа, проведенного (Were, Mollel, 2020), отражен уровень государственного долга и его устойчивость в Танзании с упором на внешний показатель. Было обнаружено, что внешний долг составляет более 70% государственного долга Танзании. Rahman и Pujiati (Rahman, Pujiati, 2021) совместно подготовили исследовательскую работу по прогнозированию государственного внешнего долга Индонезии на пять лет, с 2020 по 2024 год. Исследователи пришли к выводу, что, по прогнозам, сумма государственного внешнего долга с 2020 по 2024 год будет продолжать расти.

Статья (Calitz et al., 2016) посвящена точности бюджетных прогнозов в условиях Южной Африки. Авторы подкрепляют свои аргументы тем, что правительству следует продолжать усиливать налогово-бюджетную систему, устанавливая верхний предел расходов основного бюджета и расширяя доступность информации по аспектам налогово-бюджетной политики. Отмечается, что большая часть научной литературы по Южной Африке посвящена государственному долгу и экономическому росту (см., например: Baaziz et al., 2015; Mhlaba, Phiri, 2017).

Однако в вышеупомянутых исследованиях не были предприняты попытки смоделировать объем и динамику общего государственного долга Южной Африки с помощью моделей ARIMA. В нашем исследовании прогнозируется государственный долг Южной Африки с использованием временных рядов для периода 1960–2022 гг. Применение прогноза временных рядов (государственного долга) дает возможность сравнить данные за предыдущие периоды. Предполагается, что тенденции прошлого будут характерны и для последующих периодов, и это позволяет развивать новые направления в экономике. Вследствие сказанного целью данного исследования является моделирование размера государственного долга в Южной Африке с использованием модели ARIMA.

Данные и метод исследования

Информационной базой для исследования послужили данные Южноафриканского резервного банка (SARB). Используемая переменная – общий кредитный долг национального правительства; общий валовой кредитный долг в процентах от ВВП. Данные взяты за период с 1960 по 2022 год.

Метод Бокса – Дженкинса был предложен Джорджем Боксом и Гвилимом Дженкинсом в их основополагающей книге «Анализ временных рядов» 1970 года. Он предполагает, что процесс, создавший временной ряд, может быть аппроксимирован с помощью модели авторе-грессиного скользящего среднего (ARMA), если он не содержит единичного корня, или модели интегрированной авторегрессии скользящего среднего (ARIMA), если она нестационарна. Нами используется модель ARIMA с применением показателя государственного долга в зависимости от его значений в прошлом. Общее выражение модели Бокса – Дженкинса (ARIMA) формируется на основе двух компонентов: авторегрессии (AR) и скользящего среднего (MA). При этом AR – это модели, в которых значение переменной в одном периоде связано с ее значениями в предыдущих периодах, а модели MA учитывают возможность связи между переменной и остатками предыдущих периодов. Таким образом, ARMA можно выразить с помощью формулы:

DBTP_t = a + p₁DBTP_t-1 + P 2 DBTP_t- 2 + ...+

, (1)

+ PpDBTPt-p + ФА—1 + (p2et—2 + ... + pqet—q где DBTPt — показатель госдолга, который зависит только от собственных лагов. То есть GBTPt —это функция «лагов GBTPt-p». Аналогично, в модели чистого скользящего среднего (только MA) DBTPt зависит только от запаздывающих ошибок прогноза (pqet-q, что представляет собой ошибки авторегрессионных моделей соответствующих лагов. Анализ с использованием модели Бокса – Дженкинса состоит из четырех этапов.

1) Первый этап – идентификация модели: выбор наиболее подходящих запаздываний (лагов) для частей AR и MA, а также определение того, требует ли GBTP первой дифференциации для обеспечения стационарности. Автокорреляция (ACF) и частичная автокорреляция (PACF) используются в целях определения лучшей модели для оценки GBTP (также можно применять информационные критерии).
2) Второй этап – оценка модели: как правило, данный шаг включает в себя оценку методом наименьших квадратов путем анализа GBTP с учетом его прошлых значений и ошибок.
3) Третий этап – диагностическая проверка модели, т. е. тест на автокорреляцию. Диагностическое тестирование модели состоит из ста-
тического теста Харке – Бера, обратных корней AR и теста автокорреляции. Проверка предполагает тесты после оценки, чтобы убедиться, что выбранная модель GBTP наилучшим образом подходит для прогнозирования.

4) Четвертый этап – модельное прогнозирование. Модели ARIMA особенно эффективны при прогнозировании за счет использования запаздывающих переменных. На этом этапе предоставляются прогнозируемые значения GBTP и сравниваются их фактические значения для оценки прогнозируемых значений.

Эмпирические результаты

В данном разделе представлены результаты анализа государственного долга Южной Африки.

Годовой временной ряд показателей государственного долга за период с 1960 по 2022 год представлен на рисунке 2 .

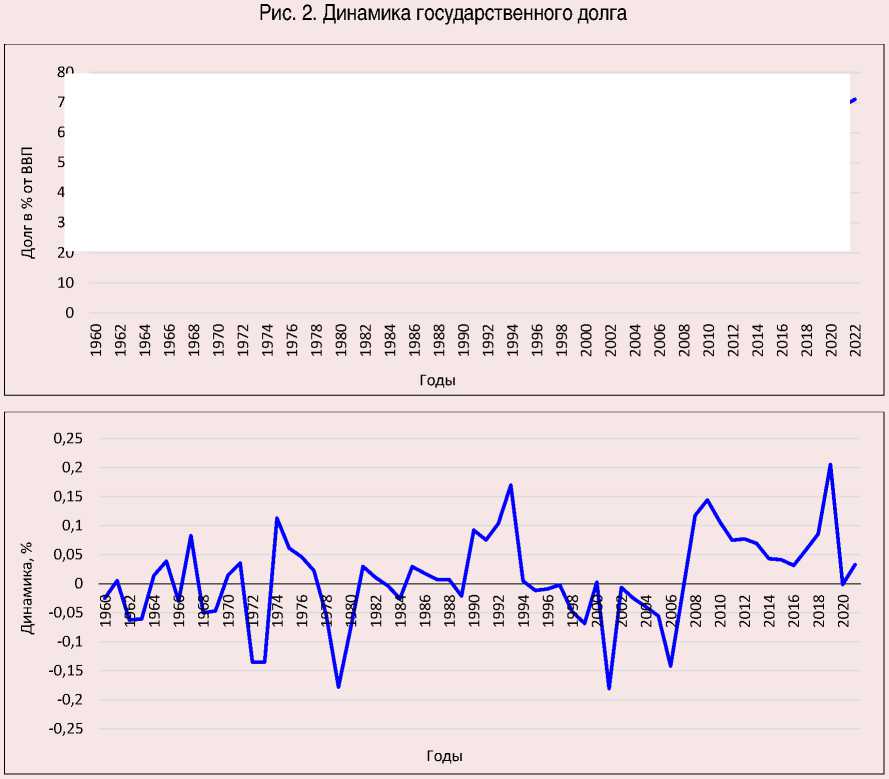
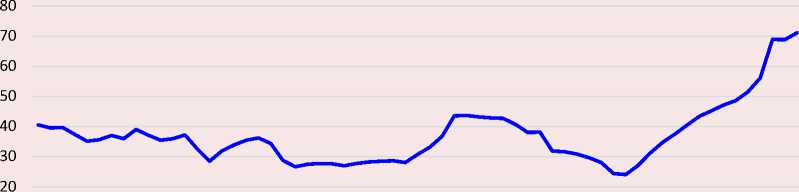
Следует отметить, что переменная нестационарна по уровням, поскольку существуют некоторые тенденции, демонстрирующие стремление показателя к росту, в частности в период с 2008 по 2022 год. Однако переменная показывает стационарность после первичной дифференциации, когда ее среднее значение и дисперсия равны нулю.

В таблице 1 отражены результаты исследования. Среднее значение государственного долга составляет 36,95% от ВВП. В 2022 году наблюдается максимум (71,1%), что объясняется высоким уровнем стагнации экономической политики из-за влияния пандемии COVID-19, а также оказанием мер государственной поддержки по восстановлению экономики. Минимальное значение составило 24% в 2008 году, что объясняется финансовым кризисом.

Следующий шаг – проверка стационарности нужной переменной. Для этого используются тесты Дики – Фуллера (1979) и Филлипса – Перрона (1988) как наиболее распространенные тесты стационарности временных рядов. В таблице 2 показаны результаты тестирования ряда на стационарность.

Сперва тест проводился лишь с использованием параметра регрессии, после – учитывались и тренд, и регрессия. В каждом случае нулевая гипотеза p = 0 не была опровергнута на 5% уровне значимости, учитывая значение теста Дики – Фуллера -0,938. Однако следует от- метить, что при первичной дифференциации t-статистика теста Дики – Фуллера -4,931 является значимой на уровне 5% при p-значении 0,000. Аналогичные значения показателей можно наблюдать и в результатах теста Филлипса – Перрона, что может свидетельствовать о том, что переменная является стационарной после первичной дифференциации.

Результаты идентификации модели

При оценке модели ARMA в первую очередь необходимо рассмотреть графики частичной автокорреляционной функции и автокорреляции ряда государственного долга Южной Африки ( рис. 3, 4 ), чтобы определить общую спецификацию будущей модели ARIMA и количество издержек для каждого компонента. Графики коррелограмм анализируются на основе ключевых свойств графиков функций ACF и PACF для процессов ARMA.

Анализируя функции ACF и PACF, можно определить, является ли выбранный набор данных процессом ARMA. Вывод о максимальном количестве лагов можно сделать только в случае чистых процессов. Рассматривая графики функций ACF и PACF на рисунке 3, следует сказать, что ряд нестационарен, поэтому он был подвергнут первичной дифференциации, содержащей лаги с порядковыми номерами 1, 8 , 12, 13 и 14. Наблюдаемый процесс является моделью ARIMA, о чем свидетельствует визуальный анализ графиков ACF и PACF.

Таблица 1. Описательные результаты исследования

Переменная	DBTP
Наблюдение выборки (Obs)	63
Среднее (Mean)	36,95
Среднеквадратичное отклонение (Std. Dev)	10,00
Мин (Min)	24,00
Макс (Max)	71,10

Таблица 2. Расширенный тест Дики – Фуллера и Филлипса – Перрона для переменных DBTP

	Только регрессия
	Результаты теста Дики – Фуллера	Результаты теста Филлипса – Перрона
Уровни	-0,938 (0,769)	-0,497 (0,884)
Первичная дифференциация	-4,931 (0,000)***	-4,931 (0,000)***
	Тренд и регрессия
Уровни	-1,375 (0,858)	-0,952 (0,942)
Первичная дифференциация	-5,217 (0,000)***	-5,247 (0,000)

Рис. 3. Доля общего государственного долга от ВВП на разных уровнях

Автокор

1 1 ■

■

■ 1 1

1 I

реляция ¹

■

■ l

1 1

■ 1
■ l

■l

■ l
■ l
■ 1

1 1

Частична

я к

■

1 1 ■ ■

1 ■

■

орреляция

1 1

■ l

1 1

АС PАС Q-Stat Prob

1 0.88... 0.88... 51.28... 7.97...
2 0.72... -0.2... 86.70... 1.48...
3 0.55... -0.1... 107.7... 3.42...
4 0.41... 0.05... 119.6... 6.44...
5 0.28... -0.0... 125.4... 2.18...
6 0.16... -0.1... 127.4... 4.35...
7 0.04... -0.1... 127.6... 1.96...
8 -0.0... -0.1... 128.0... 7.02...
9 -0.1... -0.0... 130.6... 8.62...
10 -0.2... -0.0... 136.2... 2.43...
11 -0.3... -0.1... 145.4... 1.23...
12 -0.3... -0.0... 157.7... 1.50...
13 -0.3... 0.08... 170.5... 1.44...

14 -0.3... 0.21... 179.4... 8.24...

15 -0.2... 0.19... 183.0... 5.87...

16 -0.0... 0.00... 183.5... 1.65...

17 0.01... -0.1... 183.5... 5.70...

18 0.07... 0.00... 184.0... 1.53...

19 0.12... 0.01... 185.4... 2.63...

20 0.16... -0.0... 187.8... 2.74...

21 0.20... 0.04... 192.1... 1.27...

22 0.22... -0.1... 196.9... 4.41...

23 0.21... 0.00... 201.8... 1.48...

24 0.19... 0.00... 205.9... 7.44...

25 0.16... -0.0... 208.7... 6.23...

26 0.12... 0.05... 210.4... 8.72...

27 0.05... -0.0... 210.7... 2.18...

28 -0.0... -0.0... 210.8... 5.86...

Рис. 4. Доля общего государственного долга от ВВП при первичной дифференциации

Автокорреляция	Частичная корреляция	АС	PАС	Q-Stat	Prob
1	1 ^ 1	0.41...	0.41.	.. 11.28...	0.00...
1 1	2	0.14...	-0.0.	.. 12.71...	0.00...
1 11	3	0.09...	0.05.	.. 13.28...	0.00...
1 1 1	4	0.03...	-0.0.	.. 13.37...	0.00...
1 1	5	0.03...	0.02.	.. 13.44...	0.01...
1 1 1	6	0.06...	0.05.	.. 13.75...	0.03...
1 1 1	7	0.09...	0.05.	.. 14.37...	0.04...
1 ■ 1	cz 8	-0.1...	-0.2.	.. 15.69...	0.04...
1 1 1	1 1 9	-0.0...	0.10.	.. 15.94...	0.06...
1 1 1	10	0.04...	0.05.	.. 16.07...	0.09...
1 I 1	■ 11	-0.1...	-0.1.	.. 16.94...	0.10...
■ 1	■ 12	-0.2...	-0.2.	.. 21.91...	0.03...
	■ 13	-0.3...	-0.2.	.. 34.06...	0.00...
CZ 1	14	-0.2...	-0.0.	.. 41.08...	0.00...
1 1 1	1 ■ 15	-0.0...	0.18.	.. 41.66...	0.00...
1 1 1	1 1 16	0.09...	0.11.	.. 42.48...	0.00...
1 ■ 1	1 1 17	0.13...	0.06.	.. 44.15...	0.00...
1 1	18	0.01...	-0.0.	.. 44.17...	0.00...
1 1 1	I Z3 19	0.10...	0.19.	.. 45.19...	0.00...
1 1 1	■ 20	-0.0...	-0.2.	.. 45.46...	0.00...
1 1	21	0.00...	-0.0.	.. 45.46...	0.00...
1 ■ 1	1 1 22	0.12...	0.08.	.. 47.06...	0.00...
1 1 1	23	0.06...	0.01.	.. 47.49...	0.00...
1 1	1 ■ 24	-0.0...	-0.1.	.. 47.50...	0.00...
1 1 1	1 [ 25	0.05...	-0.0.	.. 47.82...	0.00...
1 ■	1 1 26	0.24...	0.09.	.. 54.50...	0.00...
1 11	27	0.12...	0.03.	.. 56.16...	0.00...
¹ П ¹	¹ fl 28	0.11...	0.13.	.. 57.70...	0.00...

Результаты выбора модели

Согласно модели Бокса – Дженкинса (1979), следующим шагом является оценка модели ARIMA с учетом значимости коэффициента, скорректированного R-квадрата и информационного критерия Акаике (AIC), t-статистики с использованием пяти моделей ARIMA. В таблице 3 представлены модели ARIMA, которые можно считать наиболее подходящими, а именно ARIMA (1,1,1), ARIMA (8,1,1), ARIMA (13,1,1), ARIMA (1,1,12) и ARIMA (1,1,14). На основе скорректированного R-квадрата и AIC модель ARIMA (13,1,1) является наиболее подходящей относительно других моделей ARIMA. Таким образом, модель ARIMA (13,1,1) используется для прогнозирования общего государственного долга на период с 2021 по 2023 год.

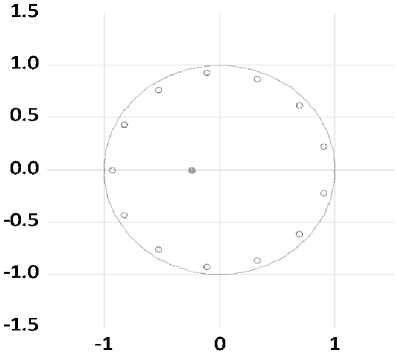
На рисунках 5, 6 представлена графическая модель Q-теста Люнга – Бокса и обратных корней модели ARIMA (13,1,1). На рисунке 5 отображены результаты, согласно которым нулевая гипотеза не отрицается. То есть большинство p-значений теста больше 0,05, что означает, что остатки для модели временных рядов независимы. Для диагностики структуры ARMA корни должны лежать внутри единичного круга. В противном случае модель считается нестабильной и, следовательно, не подходит для прогнозирования. Поскольку соответствующие обратные корни полинома лежат в единичном круге, можно сделать вывод, что выбранная модель ARIMA (13,1,1) стабильна и действительно подходит для прогнозирования государственного долга Южной Африки.

Поскольку модель ARIMA (13,1,1) действительно описывает динамику совокупного государственного долга и предполагает более высокую точность для дальнейшего прогнозирования, уравнение (2) отражает спецификацию модели следующим образом:

d ( dbtp)_t = a + /3₁&dbtp_t-1+ ... + +^dbtp_t — ₁₃ +

i e_t + р>₂е — + 8_t

Уравнение (2) используется для определения модели, которая позволит получить прогноз динамики государственного долга Южной Африки.

Таблица 3. Анализ выбора наиболее подходящей модели

Модель	Переменные	Коэффициенты	T-статистика	AIC	Скорректированный R-квадрат
ARIMA (1,1,1)	AR(1) МА(1) Sigmasq	0,657 -0,312 7,261	1840 -0,708 7746*	4920	0,124
ARIMA (8,1,1)	AR(8) МА(1) Sigmasq	-0,166 0,355 7,484	-0,996 3000* 8,705*	4953	0,097
ARIMA (13,1,1)	AR(13) МА(1) Sigmasq	-0,399 0,239 6,688	-1837 1733 6662***	4872	0,193***
ARIMA (1,1,12)	AR(12) МА(8) Sigmasq	-0,311 -0,119 8,048	-1,270 -0,793 10 193***	5,041	0,029
ARIMA (1,1,14)	AR(1) МА(14) Sigmasq	0,356 -0,201 7087	3838 -0,797 8,593	4904	0,145

Рис. 5. Q-статистический тест Люнга – Бокса для модели ARIMA (13,1,1)

Автокорреляция	Частичная корреляция		АС	PАС	Q-Stat	Prob
1 1	1 1	1	0.03...	0.03...	0.058...
1 Bl	I Bi	2	0.15...	0.15...	1.749...
i л	i Л	3	0.16...	0.16...	3.643...	0.05...
1 1 1	1 1 1	4	0.08...	0.05...	4.152...	0.12...
I E i	IB I	5	-0.0...	-0.1...	4.728...	0.19...
i Bi	1 ■ 1	6	0.18...	0.14...	7.041...	0.13...
i 3 i	1 ■ 1	7	0.10...	0.13...	7.893...	0.16...
IB i	IB I	8	-0.1...	-0.1...	9.773...	0.13...
1 1 1	1 1 1	9	0.04...	-0.0...	9.920...	0.19...
1 □ 1	I Bi	10	0.13...	0.15...	11.31...	0.18...
1 1 1	1 1	11	-0.0...	-0.0...	11.71...	0.22...
1 □ 1	icz I	12	-0.1...	-0.2...	12.99...	0.22...
1 1 1	1 1 1	13	0.05...	-0.0...	13.26...	0.27...
IB 1	1 1 1	14	-0.2...	-0.0...	16.73...	0.16...
1 1 1	1 11	15	-0.0...	0.10...	16.77...	0.20...
1 ] 1	1 11	16	0.10...	0.09...	17.72...	0.21...
1 1 1	1 1	17	0.04...	0.02...	17.93...	0.26...
IB 1	1 ■ 1	18	-0.1...	-0.1...	20.71...	0.18...
1 Hl	1 ■ 1	19	0.16...	0.13...	23.10...	0.14...
I E i	I E i	20	-0.0...	-0.0...	23.92...	0.15...
i 1 i	i E i	21	-0.1...	-0.0...	24.90...	0.16...
i 1 i	i 1 i	22	0.11...	0.11...	26.12...	0.16...
1 1	1 1 1	23	0.03...	0.03...	26.22...	0.19...
1 1 1	1 1 1	24	-0.0...	0.03...	26.57...	0.22...
1 1	1 1 1	25	-0.0...	-0.0...	26.58...	0.27...
1 ■	I Bi	26	0.25...	0.15...	33.66...	0.09...
1 1 1	1 1	27	-0.0...	0.01...	34.73...	0.09...
¹ H¹	¹ ^ ¹	28	0.14...	0.09...	37.03...	0.07...

Рис. 6. Корни остатков AR для модели ARIMA (13,1,1)

D(DBT): Обратные корни полинома (ов) AR и MA

Корни AR

Корни MA

Результаты прогнозирования

Прежде чем перейти к обсуждению прогнозируемых значений, следует отметить, что некоторые прогнозные оценки были рассмотрены для обеспечения более точного анализа. В таблице 4 представлены критерии оценки модели прогнозирования ARIMA (13,1,1). В данной статье применялись наиболее часто используемые критерии оценки, такие как среднеквадратичная ошибка (RMSE), средняя абсолютная ошибка (MAE) и средняя абсолютная процентная ошибка (MAPE). Нами исследованы методы прогнозирования, а именно динами- ческое прогнозирование. На основе полученных указанным методом данных можно сделать вывод, что он обеспечивает наилучшие результаты прогнозирования.

На рисунке 7 показана динамика государственного долга, фактическая и прогнозируемая с помощью динамического прогнозирования. Прогноз в пределах выборки охватывает период с 1960 по 2022 год, тогда как прогноз вне выборки рассчитан на один последующий период, то есть до 2023 года. Согласно представленным данным, прогнозируемые значения хорошо имитируют фактические значения ( табл. 5 ).

Таблица 4. Критерии оценки прогнозирования ARIMA (13,1,1)

Критерии оценки	Динамическое прогнозирование
RMSE	11.44
MAE	8.01
MAPE	19.58

Таблица 5. Сравнение фактического и прогнозируемого показателя государственного долга

Год	Фактические значения	Прогнозные значения
2021	68,8	71,53
2022	71,1	70,33
2023	–	68,66

Рис. 7. Фактические и прогнозируемые значения государственного долга с использованием модели ARIMA (13,1,1)

DBT – Фактическая динамика государственного долга

DBTF – Прогнозируемая динамика государственного долга

Таким образом, прогноз общего государственного долга показывает тенденцию к снижению с 71,5% в 2021 году до 70,3% в 2022 году и до 68,7% в 2023 году. Следовательно, полученные прогнозные данные практически не отклоняются от фактических значений, в частности на 2022 год.

Заключение

В рамках статьи была предпринята попытка рассмотреть процесс моделирования и прогнозирования государственного долга в Южной Африке. Нами предложено внедрение одномерной модели ARIMA, которая позволяет моделировать и прогнозировать показатель государственного долга в дальнейшем. Следует отметить, что прогнозирование имеет ключевое значение для управления государственным долгом. Полученные результаты показывают, что модель ARIMA (13,1,1) прошла все необходимые диагностические тесты, следовательно, она в большей степени подходит для прог- нозирования. В ходе анализа дополнительно были задействованы динамические методы. Прогноз показывает, что в будущем ожидается снижение темпов роста государственного долга. Следует подчеркнуть, что такое прогнозируемое сокращение долга имеет экономические последствия для Южной Африки. В связи с этим данное исследование направлено на стимулирование проведения жесткой налоговобюджетной реформы с целью свести государственный долг к минимуму. Реформа может включать повышение налоговых поступлений или сокращение государственных расходов для стабилизации государственного долга. Таким образом, практическая значимость настоящего исследования заключается в том, что предложенная модель успешно имитирует фактические значения объема государственного долга в ходе прогнозирования. На наш взгляд, следует продолжить исследование динамики государственного долга.

Список литературы Моделирование и прогнозирование государственного долга в Южной Африке

Baaziz Y., Guesmi K., Heller D., Lahiani A. (2015). Does public debt matter for economic growth? Evidence from South Africa. The Journal of Applied Business Research, 31(6), 2187–2196.
Balassone F., Francese M., Pace A. (2011). Public debt and economic growth in Italy. In: Economic History Working Paper 11. Rome: Bank of Italy. DOI: https://doi.org/10.2139/ssrn.2236725
Box G.E.P., Jenkins G.M. (1976). Time Series Analysis: Forecasting and Control. 1st edition. San Francisco: Holden-Day.
Burriel P., Checherita-Westphal C., Jacquinot P., Schön M., Stähle N. (2020). Economic consequences of high public debt: Evidence from three large scale DSGE models, European Central Bank (ECB). Working Paper Series, 2450.
Calitz E., Siebrits K., Stuart I. (2016). Enhancing the accuracy of fiscal projections in South Africa. South African Journal of Economic and Management Sciences, 19(3), a1142. DOI: https://doi.org/10.4102/sajems.v19i3.1142
Cecchetti S.G., Mohanty M.S., Zampolli F. (2010). The future of public debt: Prospects and implications. Bank for International Settlements (BIS), BIS Working Papers, 300.
Checherita-Westphal C., Hughes-Hallett A., Rother P. (2014). Fiscal sustainability using growth maximizing debt targets. Applied Economics, 46(6), 638–647.
Dickey D., Fuller W.A. (1979). Distribution of the estimators for autoregressive. Time series with a unit root. Journal of the America Statistics Association, 74(366), 427–431.
Dumitrescua B.A. (2014). The public debt in Romania – factors of influence, scenarios for the future and a sustainability analysis considering both a finite and infinite time horizon. Procedia Economics and Finance 8, 283–292.
Mahadea D. (1998). The fiscal system and objectives of GEAR in South Africa – consistent or conflicting? South African Journal of Economics and Management Sciences (SAJEMS), 1, 3.
Mellet A. (2014). Analysis of macroeconomic forecasting accuracy of South African national treasury. Mediterranean Journal of Social Sciences, 5(21).
Mhlaba N., Phiri A. (2017). Is public debt harmful towards economic growth? New evidence from South Africa. Cogent Economics and Finance, 7(1).
Minakir P.A., Leonov S.N. (2019). Regional public debt: Trends and formation specifics. Economic and Social Changes: Facts, Trends, Forecast, 12(4), 26–41. DOI: 10.15838/esc.2019.4.64.2
Munir K., Mehmood N.R. (2018). Exploring the channels and impact of debt on economic growth: Evidence from South Asia. South Asia Economic Journal, 19(2), 171–191. DOI: 10.1177/1391561418794692
Nikoloski A., Nedanovski P. (2017). Government debt dynamics and possibilities for its projection. The case of the Republic of Macedonia. In: DIEM: Dubrovnik International Economic Meeting.
Phillips P.C., Perron P. (1988). Testing for a unit root in time series regression. Biometrika, 75(2), 335–346.
Rahman Y., Pujiati A. (2021). Dynamic forecasting of government foreign debt: Case of Indonesia. JEJAK: Jurnal Ekonomi dan Kebijakan, 14(1). DOI: https://doi.org/10.15294/jejak.v14i1.29715
Schularick M. (2012). Public debt and financial crises in the twentieth century. European Review of History: Revue Europeenne d'Histoire, 19(6), 881–897. Available at: https://doi.org/10.1080/13507486.2012.739149
Were M., Mollel L. (2020). Public debt sustainability and debt dynamics: The case of Tanzania. In: Research Report 20/5, October 202. UONGOZI Institute. Available at: https://media.africaportal.org/documents/Public-debt-sustainability-and-debt-dynamics_WP20_5.pdf
Zaja M.M., Krzic A.S., Habek D. (2018). Forecasting fiscal variables in selected European economies using least absolute deviation method. International Journal of Engineering Business Management, 10, 1–19. Available at: https://doi.org/10.1177/1847979017751485
Zhuravka F., Filatova H., Aiyedogbon J.O. (2019). Government debt forecasting based on the Arima model. Public and Municipal Finance, 8(1), 120–127. DOI:10.21511/pmf.08(1).2019.11

Еще

Статья научная