Моделирование и синтез замкнутых механических систем с многократными связями на основе целочисленных решений структурного уравнения механики
Автор: Пожбелко Владимир Иванович, Ермошина Екатерина Николаевна
Рубрика: Расчет и конструирование
Статья в выпуске: 33 (292), 2012 года.
Бесплатный доступ
Рассматривается методика и примеры синтеза многозвенных механических систем на основе полученных целочисленных решений исходного структурного уравнения механики. Установлено, что данное алгебраическое уравнение с двумя неизвестными имеет конечное множество из девяти решений в целых числах, которые могут быть использованы для построения (на основе этих решений) возможных структур механических систем взаимосвязанных твердых тел.
Механические системы, структурный синтез, целочисленное решение уравнения, диофантов анализ
Короткий адрес: https://sciup.org/147151592
IDR: 147151592 | УДК: 621.01
Текст научной статьи Моделирование и синтез замкнутых механических систем с многократными связями на основе целочисленных решений структурного уравнения механики
-
1. Постановка задачи и предлагаемый путь ее решения
Математические выражения (уравнения, неравенства и другие зависимости переменных величин) являются основным средством формализации и познания при моделировании физических явлений и строения окружающего мира, представляющего собой различные механические системы [1-4], состоящие из целого числа взаимосвязанных твердых тел (рис. 1). Таким образом, в механике возникает проблема решения уравнений прикладной математики именно в целых числах, относящаяся к достаточно сложным задачам аналитической теории чисел [5-7] и получившая название «диофантов анализ уравнений» (по имени древнегреческого математика Диофанта).
В работах [5-7] отмечено, что в первую очередь такие проблемы возникают, когда приходится искать целочисленные решения уравнений, где число неизвестных превышает число уравнений (например, два и более неизвестных в одном уравнении) и которые содержат:
-
а) более простую задачу - установление существования конечного (или бесконечного) количества целочисленных решений данного уравнения или системы исходных уравнений (или полного отсутствия таких решений в целых числах);
-
б) более сложную задачу - определение расчетным путем точного количества этих целочисленных решений при увеличенном (два и более) числе неизвестных в рассматриваемом уравнении;
-
в) рассматриваемую в данной работе предельно сложную задачу - нахождение всех этих решений в целых числах для количественного описания, а также последующее моделирование и целенаправленное создание (на основе этих решений) возможных структур механических систем взаимосвязанных твердых тел:
-
– как уже существующих (образовавшихся в природе окружающего мира в виде различных химических соединений и живых биологических объектов);
-
– так и искусственно создаваемых человеком разнообразных подвижных и неподвижных механических устройств (например, движущиеся механизмы машин и неподвижные шарнирнорычажные фермы).
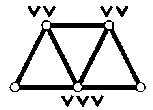
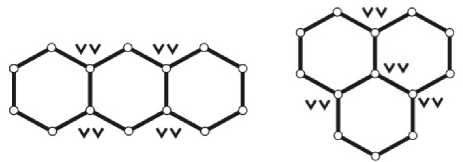
Отметим, что разнообразные механические системы взаимосвязанных твердых тел могут содержать как только простые (simple joints) соединения между собой двух отдельных компонентов (звеньев) системы (это будет частный случай – обозначим его ν = 0 ), так и сложные многократные (complex many-sided) соединения между собой трех и более отдельных компонентов (звеньев) системы (этот более общий случай ее строения обозначим ν ≠ 0). Некоторые примеры возможных подвижных соединений (связей) звеньев между собой в различных замкнутых механических системах даны на рис. 2 (где кратность j образующихся соединений будет на единицу меньше числа сходящихся в узле звеньев механической системы).
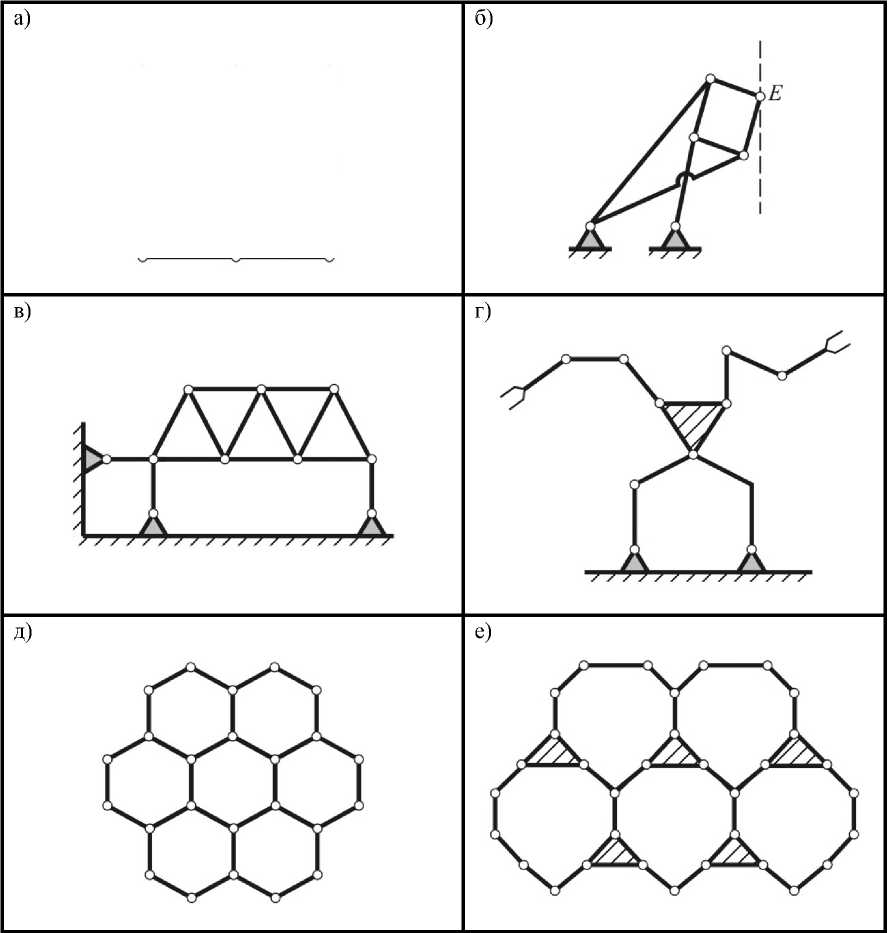
Рис. 1. Примеры механических систем с многократными связями, созданных природой и изобретенных человеком (на основе познания закономерностей окружающего мира): а - кристаллическая решетка твердых веществ [3]; б - шарнирный прямолинейно направляющий механизм [1]; в -стержневая ферма однопролетного моста [1]; г - человекоподобный робот-манипулятор; д - сотовые конструкции пчелиных ульев (с ячейками шестигранной формы); е - сотовые конструкции решеток охлаждения современных ядерных реакторов (с ячейками девятигранной формы) [4]
Расчет и конструирование
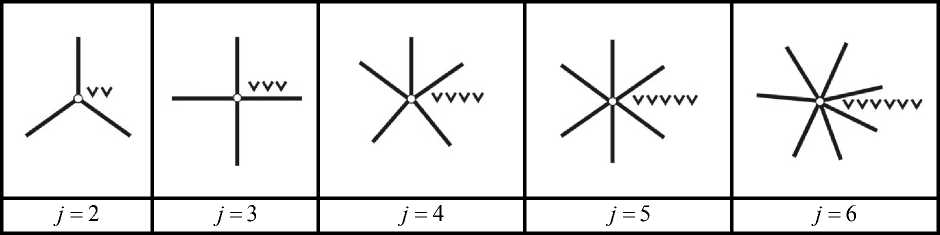
Рис. 2. Варианты многократных связей элементов механических систем (узлов с кратностью )
Для формализации строения многозвенных механических систем используем полученное в работе [2] уравнение многократных связей замкнутых механических систем (исходное структурное уравнение механики), которое в общем случае (v ^ 0) имеет вид v2 + 2v3 + 3V4 + 4V5 +... + (k — 1)vk = v; v < C = 2(K — 1), (1)
где v j - число j -кратных соединений звеньев замкнутой механической системы ( j max = K ); K -число образуемых звеньями системы взаимно независимых замкнутых контуров ( K > 1); v -приведенное число многократных соединений звеньев (узлов) механической системы; параметр k в последнем слагаемом данного уравнения зависит от величины K и равен k = K + 1 (при C < K в области K < 2) или равен k = K (при C > K в области K > 2).
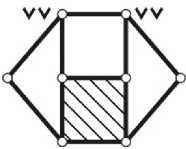
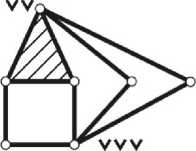
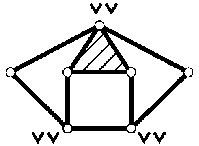
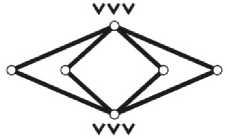
Решение исходного уравнения (1) заключается в определении всех целочисленных значений неизвестных ( v 2, v g , v 4 , v g ,..., v k ) при заданной целой величине K = 1; 2; 3;... и соответствующей ей целой константе C = 2( K — 1), задающей диапазон изменения v < C . На рис. 3 даны примеры разнообразных механических систем, структура которых удовлетворяет граничному v = C .
С математической точки зрения исходная зависимость (1) представляет собой линейное алгебраическое уравнение 1-й степени с целой константой C и постоянными целыми коэффициентами ci , образующих арифметическую прогрессию (число слагаемых которой зависит от задаваемой величины K = 1; 2; 3;…):
-
( c 0 У 1 + С 1 У 2 + c 2 У з + c 3 У 4 + c 4 У 5 ... + С У , ) — C = 0, (2)
где с о = 0, с = 1, с 2 = 2, C g = 3, с 4 = 4,..., с , = ( k — 1);
y 2 = v 2 , y 3 = v 3 , y 4 = v 4 , y 5 = v 5 ,^, y i = v k .
Предлагаемый алгоритм поиска всех решений уравнения (1) состоит из трех этапов;
-
а) определение диапазона возможных целочисленных значений неизвестных (I этап);
-
б) составление аналитической зависимости между неизвестными (II этап);
-
в) определение всех решений искомого уравнения в целых числах – из совместного рассмотрения пунктов а и б (III этап).
-
2. Решение структурного уравнения механики в целых числах
Применим предлагаемый трехэтапный алгоритм для решения в целых числах исходного структурного уравнения механики (1) при K = 1, K = 2, K = 3.
-
I. K = 1
Исходное структурное уравнение механики (1) при K = 1 вырождается ( v = v 2 , C = 0) и имеет единственное решение
v2 =v = 0, которое представлено на рис. 4 в виде одноконтурной замкнутой механической системы.
-
II. K = 2
Исходное структурное уравнение механики (1) при K = 2 примет вид v2 + 2v3 =v; v< 2(K — 1) = 2
и в диапазоне возможных целочисленных значений неизвестных 0
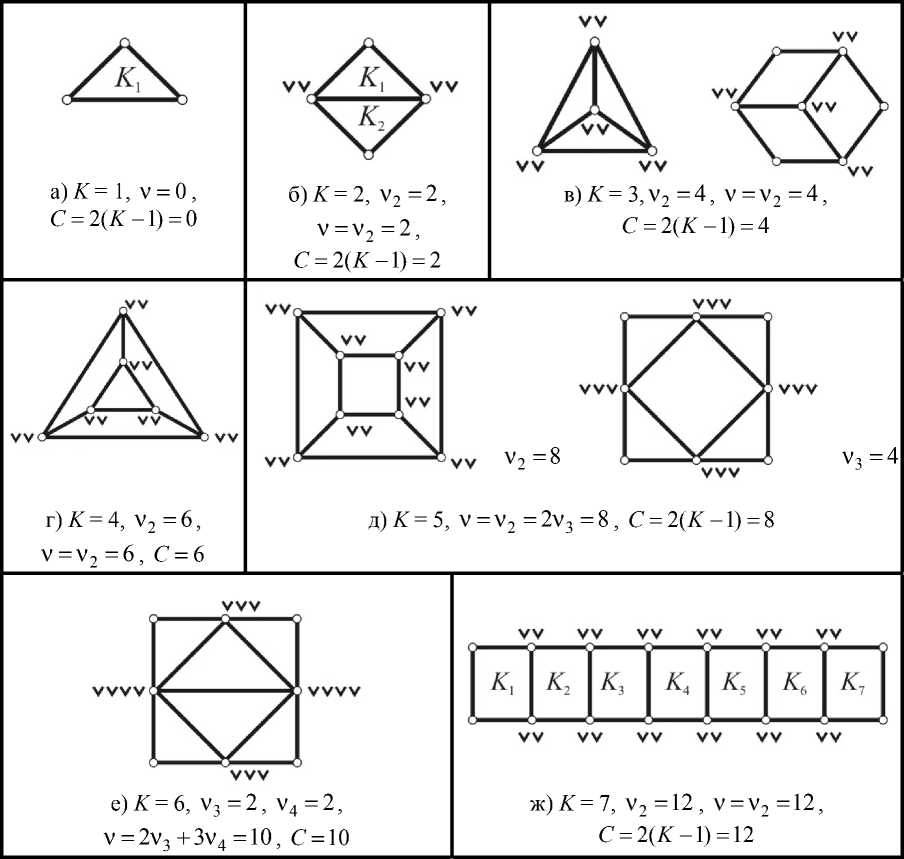
Рис. 3. Моделирование строения замкнутых одноконтурных ( K = 1)
и многоконтурных ( K 2) шарнирно-рычажных структур (выполнение граничного условия структурного уравнения механики (1) вида )
v 2 = 0, v 3 = 0, v 2 = 1, v 3 = 0, v 2 = 2, v 3 = 0, v 2 = 0, v 3 = 1
(представленные на рис. 4 в виде различных двухконтурных механических систем).
-
III. K = 3
Исходное структурное уравнение механики (1) при K = 3 примет вид v2 + 2v3 = v; v < 2(K —1) = 4
и в пределах v < 4 может иметь только 5 значений величины v :
v = С = 0; v = С2 = 1; v = С = 2; v = С4 = 3; v = С5 = 4, приводящих к следующей совокупности целочисленных решений уравнения (1), определяющих возможные варианты структуры трехконтурных механических систем:
-
а) C 1 = 0:
v 2 + 2 v 3 = 0 ^ v 2 = 0, v 3 = 0 (первое решение);
-
б) C 2 = 1:
v 2 + 2 v 3 = 1 ^ v 3 = —2— ^ из условия v 3 > 0 величина v 2 может быть только нечетной и равной v 2 = 1, v 3 = 0 (второе решение);
Расчет и конструирование
-
в) C3 = 2:
V
-
V 2 + 2 V 3 = 2 ^ V 3 = 1 - -"2- ^ из условия V 3 > 0 величина V 2 может быть только четной и в пределах V 2 < 2 таких четных цифр только две: V 2 = 0, V 3 = 1 (третье решение); V 2 = 2, V 3 = 0 (четвертое решение);
-
г) C 4 = 3:
-
V 2 + 2 V 3 = 3 ^ V 3 = —2— ^ из условия V 3 > 0 величина V 2 может быть только нечетной и в пределах V 2 < 3 таких нечетных цифр только две (1; 3): V 2 = 1, V 3 = 1 (пятое решение); V 2 = 3, V 3 = 0 (шестое решение);
-
3. Теорема о конечном множестве целочисленных решений структурного уравнения механики с несколькими неизвестными
Д) C 5 = 4:
V
V 2 + 2 V 3 = 4 ^ V 3 = 2 - -"2- ^ из условия V 3 > 0 величина V 2 может быть только четной и в пределах V 2 < 4 таких четных цифр только три (это 0; 2; 4): V 2 = 0, V 3 = 2 (седьмое решение); V 2 = 2, V 3 = 1 (восьмое решение); V 2 = 4, V 3 = 0 (девятое решение).
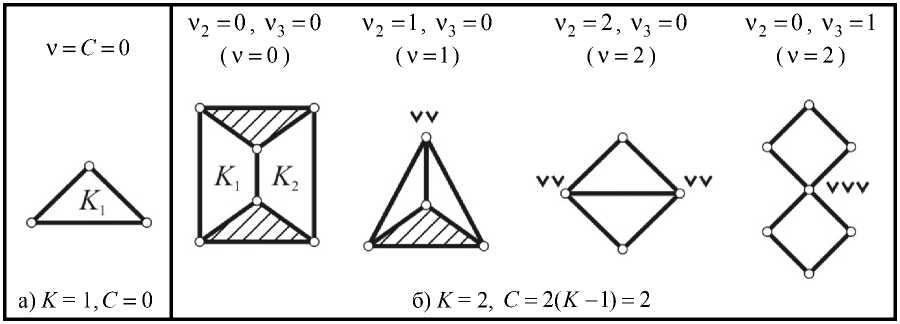
Рис. 4. Создание одноконтурных ( K = 1) и двухконтурных ( K = 2) замкнутых механических систем (на основе решений в целых числах структурного уравнения механики (1) в случае C K )
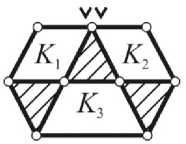
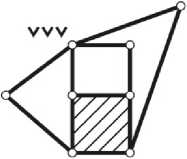
Таким образом, исходное уравнение механики (1) при K = 3 содержит 2 неизвестных ( V 2 , V 3 ) и имеет только 9 решений в целых числах (представленных на рис. 5 в виде трехконтурных замкнутых механических систем).
Анализ полученных в п. 2 целочисленных решений линейного структурного уравнения механики (1) позволяет предположить, что их различное число предопределено разными наборами четных и нечетных цифр согласно предлагаемой ниже теореме.
Теорема
Линейное структурное уравнение механики вида
V2 + 2V3 + 3V4 + 4V5 +... + (k — 1)vk = V ; V < C = 2(K - 1) ^ V2 + 2V3 < Cq(3)
при любых K > 1 (т. е. с любым числом неизвестных) имеет конечное множество Z целочисленных решений (V2,V3,V4,...), определяемое набором четных и/или нечетных взаимно простых целых чисел в составе константы C0 и рассчитываемое по формуле z = X N, N = (m + k0) + (m1^),(4)
C0 = 2(K-1)-[3v„ + 4V5 +...+(k — 1)Vk], Cq где Ni - число целочисленных решений в пределах данного значения C0; m0, к0 - сумма четных цифр (m0) и их количество (к0) в цифровом диапазоне от нуля до предела, равного C0 (включительно); m1, к1- сумма нечетных цифр (m1) и их количество (к1) в цифровом диапазоне от нуля до предела, равного C0 (включительно). 1) v2= 0, v3= 0(v = 0) 2) v2= 1, v3= 0( v = 1) 3) v2= 0, v3= 1(v = 2) 4) v2= 2, v3= 0( v = 2) 5) v2 = 1, v3 = 1(v = 3) 6) v2= 3, v3= 0( v = 3) 7) v2= 0, v3= 2 (v = 4) 8) v2 = 2, v3= 1 (v = 4) 9) v2=4, v3= 0(v = 4) Рис. 5. Создание трехконтурных (K = 3, C = 2(K – 1)) замкнутых механических систем (на основе решений в целых числах структурного уравнения механики (1) в случае C > K) Пример № 1. Исходные данные: K = 2; v2+ 2v3 = 2(K -1) = 2 ; C0 = С = 2; Ni = N . Результаты расчета: m0= 0 + 2 = 2, к0= 2; m1 = 1, k1 = 1 ^ N = (2/2 + 2) + (1) = 4; Z = N = 4 . Пример № 2. Исходные данные: K = 3; v2+ 2v3 = 4; C0 = C = 4; Ni = N . Результаты расчета: m0 = 0 + 2 + 4 = 6, к0 = 3; m1 = 1 + 3 = 4, k1 = 2 ^ N = (3 + 3) + (3) = 9; Z = N = 9. (Совпадают с представленными на рис. 4 и 5 для случаев K = 2 и K = 3). Примечание В работе [6] рассматривается метод поиска целочисленных решений линейного уравнения с двумя неизвестными вида решение которого представлено в виде x = Х0 - bt, y = y0 + at, где t - параметр (t = 0, ± 1, ± 2, ..), (Х0, y0) - некоторое решение данного уравнения, в указанном уравнении a, b - целые числа, отличные от нуля и взаимно простые; E - целое. Применительно к рассматриваемой механической системе с K = 2 (см. рис. 4) на a, b, E необходимо наложить дополнительные условия: x > 0, y > 0; a = 1, b = 2; E< 0; (x0 = E, y0 = -E) -одно из решений; E е [-2,0]. Расчет и конструирование С учетом данных условий получаем следующую систему неравенств: Гx = E — 2t > 0; из которой определяем интервал изменения параметра t (с учетом отрицательной величины E): t< —; t > E и получаем следующий набор целочисленных решений: Х1 = 0, У1 = 0; x2 = 1, у2 = 0; Х3 = 2, у3 = 0;x4 = 0, у4 = 1. Сравнительный анализ полученного множества из 4 решений показывает, что данный результат (пары чисел x и у) полностью согласуется как с целочисленными решениями при K = 2 (см. п.2), так и с определением числа решений по аналитической зависимости (4) теоремы, предложенной в п.3 данной работы. Выводы 1. Установлено, что исходное структурное уравнение механики вида [2] 2. Полученные целочисленные решения указанного структурного уравнения механики отражают все возможное многообразие структур с многократными связями и могут быть практически реализованы в виде разнообразных механических систем взаимосвязанных твердых тел (подвижных или неподвижных звеньев) для разных областей техники. 3. В синтезированных на основе целочисленных решений разнообразных механических систем (см. рис. 4 и 5) выявлена общая закономерность упрощения структуры (за счет снижения сложности составляющих звеньев) при переходе от нижней границы v = 0 к верхней границе v = C их строения с многократными связями. имеет конечное множество целочисленных решений Z (4), зависящих от набора четных и нечетных чисел в пределах константы данного уравнения, возрастающее с увеличением числа K образуемых звеньями механической системы замкнутых контуров.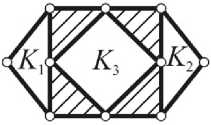
Список литературы Моделирование и синтез замкнутых механических систем с многократными связями на основе целочисленных решений структурного уравнения механики
- Крайнев, А.Ф. Механика (искусство построения) машин. Фундаментальный словарь/А. Ф. Крайнев. -М.: Машиностроение, 2000. -904 с.
- Пожбелко, В.И. Структурный анализ и синтез механизмов заданного уровня сложности по универсальной структурной таблице стандартных кодов строения/В.И. Пожбелко//Теория механизмов и машин. -2012. -Т. 10, № 1 (19). -С. 24-45.
- Глинка, Н.Л. Кристаллические решетки твердого вещества//Общая химия/Н.Л. Глинка. -Л.: Химия, 1986. -Гл. V. -704 с.
- Крапивцев, В.Г. Организация конвективного переноса в пучке твэлов за сотовыми решетками для водо-водяных энергетических реакторов/В.Г. Крапивцев, В.И. Солонин, С.И. Цирин//Известия вузов. Машиностроение. -2011. -№ 4. -С. 7-12.
- Серпинский, В. О. О решении уравнений в целых числах: пер. с пол./В. О. Серпинский. -М.: Изд-во физ.-мат. лит., 1961. -88 с.
- Гельфонд, А. О. Решение уравнений в целых числах/А. О. Гельфонд. -М.: Наука, 1983. -63 с.
- Математический энциклопедический словарь/гл. ред. Ю.В. Прохоров. -М.: Совет. энцикл., 1988. -847 с.


