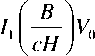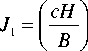Моделирование эффекта «кажущегося слоя F1», наблюдавшегося в эксперименте «Радар-Прогресс», с помощью программного обеспечения автоматической обработки ионограмм вертикального зондирования

Ионосферная плазма – омическая среда, где электрическое поле и ток связывает закон Ома. В магнитосфере прямой связи между электрическим полем и током нет. Из-за эквипотенциальности магнитных силовых линий геомагнитного поля ток в ионосфере определяется магнитосферным электрическим полем, а ток в магнитосфере – распределением газового давления. Связь между распределением давления и конвекцией существует, но достаточно сложная.

Как было показано в [Ponomarev et al., 2006a, b, c], генератором во фронте головной ударной волны производится электрический ток. В работе [Пономарев, 1985] впервые были предложены реально физически обоснованные источники мощности для электроджетов в ионосфере и показана электрическая схема их подключения (рис. 1). В работе [Седых, Пономарев, 2002] было приведено частное решение задачи магнитосферно-ионосферного взаимодействия в области авроральных электроджетов, но для наиболее простого случая.

Задача состоит в том, чтобы с помощью анализа модели, сохраняющей важнейшие черты реальности, понять, как согласованно устанавливается ток в общей электрической цепи ионосфера–магнитосфера, как работает магнитосферный генератор ионосферных токов, за счет каких источников мощности (в том числе и неэлектромагнитной природы) этот генератор функционирует. Частично ответ на последний вопрос уже существует. В работе [Пономарев, 1985] было показано, что районы магнитосферы, работающие как МГД-компрессор, где плазма сжимается под действием амперовой силы [ j x B ]/ c, удовлетворяют условию V V p g >0, а районы, где газо-

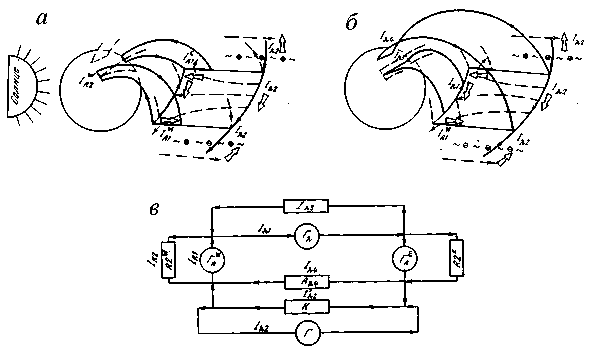
Рис . 1 . Схема расположения магнитосферно ионосферных токов в пространстве : а – система питания меридиональных токов , б – система питания широтных токов , в – эквивалентная схема цепи магнитосферно ионосферных токов . [ Пономарев , 1985]

динамические силы производят работу над электромагнитными – районы МГД-генераторов – условию V V p g <0. Переход энергии из одного вида в другой можно записать в простой форме: V V p g = jE .

Постановка задачи

Для описания магнитосферной плазмы обычно применяются уравнения двухжидкостной или одножидкостной магнитогидродинамики с изотропным или анизотропным давлением.

При этом любые диссипативные процессы в системе считаются несущественными. Это утверждение обычно справедливо в отношении омических потерь и потерь на излучение. Однако в бесстолкновительной магнитосферной плазме есть еще потери частиц (а вместе с ними и энергии) через «открытые» кон- цы силовых трубок в атмосферу. Этот вид потерь может быть весьма существенным, и его следует учитывать [Кеннел, 1972].

Приведем систему уравнений, описывающих магнитосферную плазму, следуя [Ponomarev, Sedykh, 2006; Пономарев, 1985]:

dn _i / dt + n _i div V i =– n _i/τ_i; n _i = n _0i( U ₀/ U )exp(–∫ dt /τ_i); (1) dp i / dt +γ p i div V i =– p i /τ i ; p i = p 0i ( U 0 / U )^γexp(–∫ dt /τ i ); (2) ∇ p =[ j x B ]/ c ; E =–[ V x B ]/ c ; p = p e + p p ;           (3)

s i = c v ( Y -1) J dt / T i ; J dt / t = J dR / V r T = J Rd X / V x T .         (4)

Здесь i = e, p – индекс электронов или протонов, n _i – плотность числа частиц, р i – давление частиц данного сорта, t – текущее время, γ – показатель адиабаты, U – объем плазменной трубки (плазменное содержимое МСТ), E – напряженность электрического поля, В – напряженность магнитного поля, V i – скорость электрического дрейфа соответствующей компоненты плазмы, V = V _e+ V _p – скорость дрейфа плазмы в целом, j – плотность электрического тока. Если j / en <<  V , то разницей в скоростях дрейфа электронной и протонной компонент можно пренебречь. Далее мы так и будем делать, если только это не будет оговорено особо. В магнитосферной плазме повсюду выполняется условие квазинейтральности, т. е. ( n p – n e )/( n p + n e )<<1. Первое уравнение системы – это уравнение непрерывности для электронов и ионов с учетом потерь частиц из-за питч-угловой диффузии в конус потерь. Характерное время τ – это время, за которое плазменная трубка теряет 1/е первоначального числа частиц. Уравнения (2) описывают поведение давления электронного и протонного газа при движении и из-за высыпаний. Очевидно, что поведение газа – не адиабатическое. Уравнения (3) – это уравнения движения плазмы для квазистационарного случая. Первое уравнение в (4) – выражение для плотности энтропии. Здесь c V – теплоемкость при постоянном объеме. Очевидно, энтропия увеличивается со временем и процесс конвекции плазмы в нашем приближении оказывается необратимым. Вторые выражения в (1) и в (2) – решения соответствующих уравнений.

Магнитные силовые линии геомагнитного поля «протыкают» поверхность земного шара, внутри которой расположен источник поля. Проведем элементарную окружность с центром в точке пересечения. Пучок силовых линий, проходящих внутри нее, будем называть силовой трубкой. Ее самая широкая часть приходится на магнитный экватор, след от пересечения экваториальной плоскости называется экваториальным следом. В процессе электрического дрейфа, когда массовая скорость равна

V=c[E×B]/B2, плазменная трубка переходит из одной силовой трубки в другую без избытка и недостатка, если магнитные силовые линии эквипотенциальны. Представим для определенности, что электрический дрейф происходит в сторону увеличения магнитного поля. Тогда объем плазменной трубки постоянно уменьшается ~L4, а это означает, что при всесторон- нем адиабатическом сжатии давление увеличивается в L4γ раз (L –параметр Мак-Илвейна). На этот процесс накладывается процесс опустошения МСТ за счет ухода частиц в конус потерь, τ – характерное время опустошения МСТ. В этом случае газовое давление равно dP   dV    p

V  + γp   = -γ → dx     dx     τ

V dP = I dV YI -p γ + 1 ^ \p= =[y I dV Ъ f Y , , -    dx -    dx → dx ( dx TV i J p J \ Vdx ) J V T ln p = γ(lnV -lnV)+ln p0 -γ dx

0                  Vτ p=p

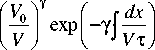
Более подробная информация о выводе и применении выражения для газового давления дана в [Пономарев, 1985], где это выражение приведено в более удобной форме для дальнейшего анализа (для частиц 5–25 кэВ):

0 p g = p g

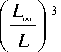
exp

5 r dr |

3^J V r T ) .

Очевидно, что dt = dR / V _R= R 0 d X / V _X , A t = J dt - транспортное время, т. е. время, за которое МСТ дойдет от границы до данной точки на потоковой линии, а V _R и V _λ – радиальная и азимутальная компоненты скорости конвекции.

Аналогично можно получить следующее выражение, учитывающее частицы более высоких энергий ( V r ~20–30 км/с; V G – порядка нескольких сотен км/с):

4γ i 0 , 0 \I L= I .

PgT =( pg1 + pg2 ) ^—J X

,

4γ

I Loo I где член pg 11     I относится к час-

тицам с энергией

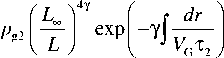
1–30 кэВ; член

– к частицам с энергией

30–300 кэВ.

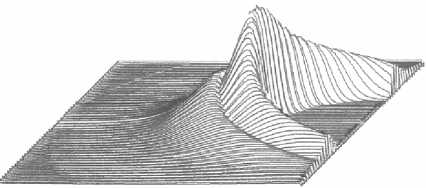
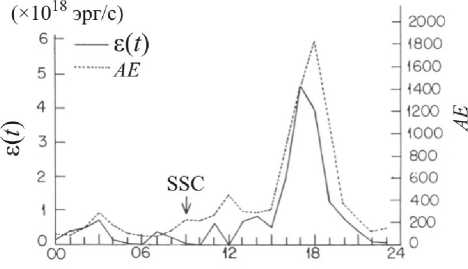
Согласно оценкам и данным спутниковых измерений,

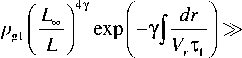
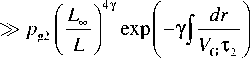
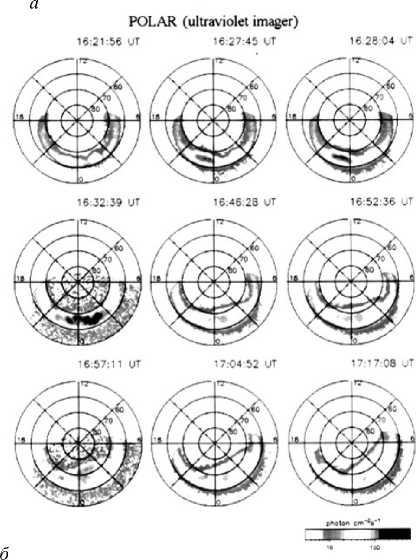
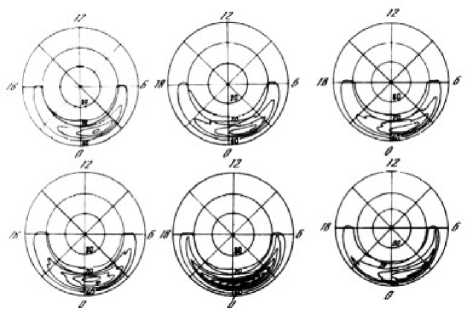
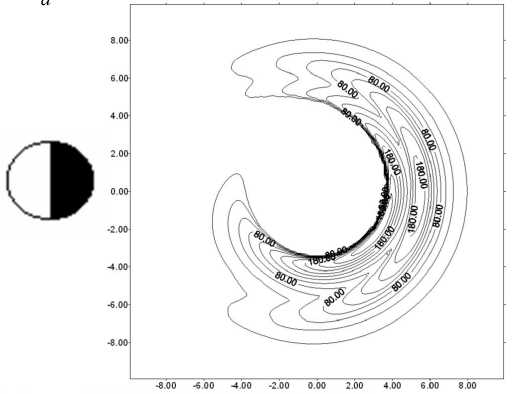
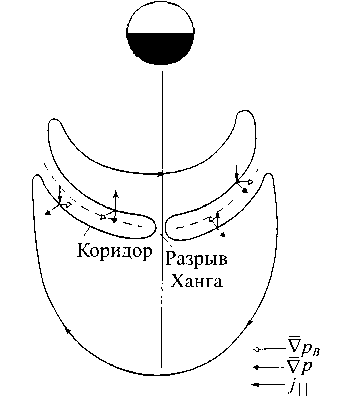
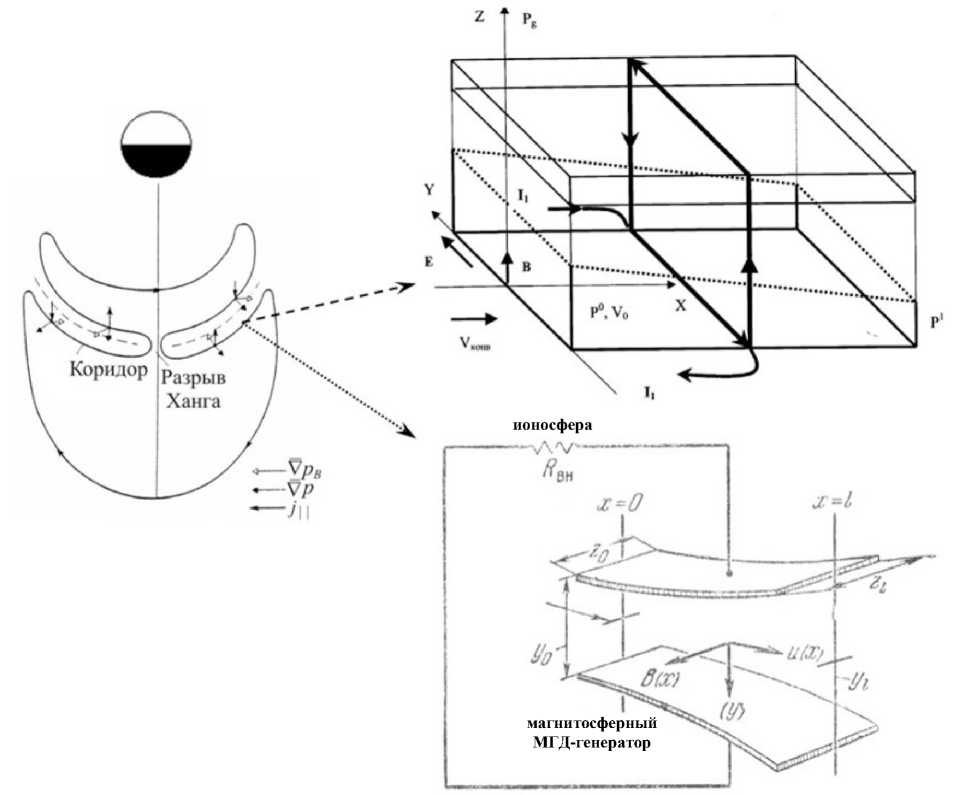
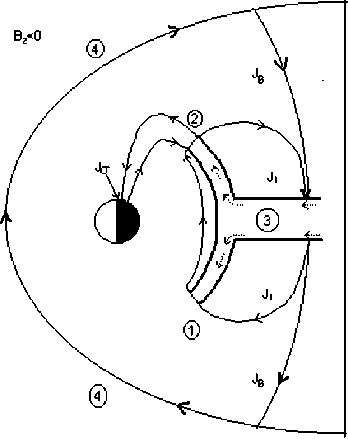
Время питч-угловой диффузии у электронов и протонов разное, поэтому и потоки частиц разные. Возникающие объемные заряды компенсируются потоками холодных ионосферных частиц. Частицы с энергией 5–30 кэВ вносят наибольший вклад в фор- мирование рельефа плазменного давления в магнитосфере на ночной стороне (4

Уравнение (5) показывает изменение газового давления при движении плазмы вдоль линии конвенции со скоростью V=(V_R²+V_λ²)^1/2. Задавая на границе L=L∞ начальное давление р0, мы можем найти результирующее в любой точке потоковой линии. Таким образом вычисляется поле давлений во всей магнитосфере. Характерный рельеф газового давления, получающийся при совместном действии конвекции плазмы и потерь из-за питч-угловой диффузии электронов и протонов, изображен на рис. 2 [Пономарев, 1985]. Он имеет вид амфитеатра с ярко выраженным максимумом около полуночного меридиана и резким «обрывом» в сторону Земли. Этот обрыв получил название внутренней границы плазменного слоя. Проекция амфитеатра на высокоширотную ионосферу соответствует форме и положению аврорального овала (рис. 3, а). Как и реальный овал, эта проекция совершает движения с изменением электрического поля конвекции, расширяясь при увеличении поля (рис. 3, б [Solovyev et al., 2003]). При этом амплитуда в максимуме увеличивается при приближении внутренней границы плазменного слоя к Земле. Рассмотрим теперь случай, когда граничные условия в (5) зависят от времени. Пусть давление на границе возрастет в два раза. Этот «импульс» начнет двигаться вниз по течению со скоростью конвекции, и повсюду за ним будет оставаться область удвоенной амплитуды.

Для анализа особенно подходит район «ущелья», которое образуется при наплывании плазменного возмущения на невозмущенный рельеф давления (результат нестационарности граничных условий). Эта деталь рельефа хорошо видна на рис. 2. На рис. 4 представлена схема среза этого рельефа. Сечением ущелья являются «коридоры». Видно, что стенки коридоров служат источниками двух полос продольных токов, направления которых противоположны на разных стенках. В целом формируется токовая конфигурация, соответствующая схеме Ииджимы и Потемры [Iijima, Po-temra, 1978], полученной по данным спутниковых измерений. Важно, что потоковые линии конвекции идут практически вдоль оси коридора, а сам коридор вытянут по отношению к изолиниям pB=const под небольшим углом и, следовательно, магнитное поле внутри него почти однородно. Поэтому параметр высыпаний τ можно считать постоянной величиной.

Рис. 2. Рельеф газового давления на ночной стороне магнитосферы при нестационарных граничных условиях [Пономарев, 1985].

6 января IMS г.

Рис. 3. Изолинии равной интенсивности плотности потока высыпающихся электронов для нестационарных граничных условий (модельные расчеты [Пономарев, 1985]) (а). Динамика авроральных явлений по данным спутника «Po-lar», 6 января, 1998, 16:21–17:17 UT [Solovyev et al., 2003]. Там же авторы выполнили сравнение модельных расчетов [Пономарев, 1985] с данными спутниковых наблюдений для события 6 января 1998 г. (16:21–17:17 UT) (б).

Магнитосферно-ионосферное взаимодействие в области авроральных электроджетов

В исследуемой нами модели заменим коридор прямоугольным каналом с идеально проводящими стенками; он будет накрыт сверху проводящей

«крышкой» – ионосферой. Разницу в пространственных масштабах, которая существует из-за конвергенции силовых линий, мы скомпенсируем коррекцией параметров. В канале с однородным вертикальным магнитным полем имеется стационарное течение идеальной плазмы с соответствующим градиентом давления. Рассмотрим явления, протекающие в плазменном коридоре, на простой модели, сохраняющей в то же время важнейшие черты реальности. Как следует из рис. 4, ориентировка коридора такова, что течение плазмы происходит почти по его оси. Коридор вытянут в долготном направлении, поэтому магнитное поле мало меняется в его пределах. Все эти обстоятельства позволяют заменить коридор каналом шириной 2D, длиной L и высотой Н, вытянутым вдоль оси X. Ось Y будет ориентирована поперек канала, а ось Z – вдоль его высоты, как показано на рис. 5. Канал заполнен идеальной плазмой с давлением p⁰ на входе и p¹ на выходе. Магнитное поле B={0, 0, B_z} будем считать однородным. Вдоль оси Х в положительном направлении течет плазма со скоростью V=Vx(x). Стенки канала обладают бесконечной проводимостью. Ионосфера моделируется верхней крышкой толщиной h c педерсеновской проводимостью о. Вследствие существования градиента давления вдоль а

б

Рис. 4. Схема среза рельефа газового давления. Сечением определенной области рельефа газового давления, так называемого ущелья, являются коридоры – каналы магнитосферных МГД-генераторов, на стенках которых генерируются продольные токи.

канала поперек него течет ток

• - c ( dp ) jy = BI 1^)"

Этой объемной плотности тока соответствуют поверхностная плотность и полный ток:

IG (x) - J jydz - Hjy , JG - JIGdx.              (7)

Соответственно, полный ток ионосферной нагрузки будет следующий:

J_о - JJ оEI dx'dz'-о h J

Edx -

о hB

Vdx. c

Штрихи над дифференциалами означают, что интегрирование ведется по пространству ионосферы. При этом из-за эквипотенциальности магнитных силовых линий электрическое поле в ионосфере E_I связано с электрическим полем в магнитосфере соотношением: E_tdx'=Edx. Помимо тока, замыкающегося через ионосферу, часть тока МГД-генератора может замыкаться через магнитосферу так, как это происходит с током коридора (рис. 4). Обозначим этот ток индексом 1. Тогда

J 1 - JJ j_y 1 dxdz - J11 dx.

Из условия непрерывности токов находим:

dp - о * B2 V +11 B dx       c2

где о*=о(h/H), с - скорость света.

Уравнение баланса газокинетической энергии в стационарном одномерном случае имеет вид dpdV p

V  + уp — - -y .

dxdx

т

Тогда p - p - (V1’

Обозначим начальный уровень газового давления, необходимый и достаточный для снабжения ионосферы электрическим током, через р⁰¹, так что p⁰=p⁰¹+p⁰², где p⁰² – начальный уровень газового давления, образующего ток J1. Тогда из уравнения (9), учитывая выражение (11), получим:

dV 1

--+ dx т

-Y

01 ^p

dV 1

1 dx т

0 ^p

^^^^^^^B

I. Ищем решение данной системы уравнений в линейном приближении. Решение этой системы уравнений, удовлетворяющее условиям нашей задачи, есть

V - V-

Yx

(Y+ 2)т ‘

Рис. 5. Схема канала магнитосферного МГД-генератора с идеально проводящими стенками, накрытого сверху проводящей «крышкой» – ионосферой. Штриховой линией показан рельеф газового давления р_g, жирными линиями – направление токов.

Это выражение показывает, как меняется скорость плазмы от входа канала магнитосферного МГД-генератора до выхода из него.

Полученное решение подставляем опять в выражение для газового давления, т. е. ищем самосогласованное решение.

• 1.    Высыпания частиц через открытые концы силовых трубок в ионосферу увеличивают проводимость ионосферы, а при возрастании проводимости ионосферы увеличивается ток с магнитосферного МГД-генератора, ответвляющийся в ионосферу, но тогда уменьшается ток через магнитосферный МГД-компрессор, нагнетающий плазму в сторону Земли.

• 2.    При уменьшении работы магнитосферного МГД-компрессора уменьшается поток энергичных частиц в ионосферу через открытые концы магнитных силовых трубок, проводимость ионосферы уменьшается, но соответственно ток, ответвляющийся на МГД-компрессор, увеличится. При увеличении работы магнитосферного МГД-компрессора будет увеличиваться поток частиц из магнитных силовых трубок в ионосферу, что скажется на проводимости ионосферы.

Из (12) получаем условие:

p

(y+ 2) Г B У 2Y I c J

О * T Уд.

Из (13) получаем условие

11 =

2Y (y+2)

0 ^p

(y+2) Г BY 2Y I c J

о * t V0²

VсH

B T Vg².

Из (16) видно, что ток I1 «организован по остаточному принципу» – сначала покрываются все необходимые расходы ионосферы, а то, что остается, уходит в область геомагнитного хвоста. Ток I1 становится там частью тока утро–вечер. Частью, потому что существует еще ток утро–вечер JВ другого происхождения. Это внешний по отношению к магнитосфере ток. Как показано в работах [Ponomarev et al., 2006a, b, c; Пономарев и др., 2009], он формируется генератором во фронте головной ударной волны. Головная ударная волна является генератором электрического тока и электрического поля, которые образуют поток энергии в магнитосферу, достаточный для покрытия магнитосферных потерь. Этот поток энергии зависит как от параметров солнечного ветра, так и от

способности магнитосферы пропустить сторонний ток. В магнитосфере постоянно существуют собственные электрические токи, связанные с существующим распределением газового давления, «диамагнитные» токи, а также собственные электрические поля, связанные с существующей конвекцией. В стационарных условиях именно уменьшение собственного тока немедленно компенсируется сторонним, так что градиент давления остается неизменным. Знак мощности не зависит от знака ММП, и мощность всегда направлена внутрь магнитосферы. По величине она разная и реализуется в разных местах магнитосферы в зависимости от знака ММП. При отрицательном значении Bz ММП электрическое поле конвекции больше, а антиконвекции – меньше, чем при таком же по модулю значении положительного ММП. Поэтому в первом случае энергия в основном рассеивается в авроральной зоне, а во втором – в полярной шапке. Электрический ток от ГУВ (головная ударная волна), также меняющий знак при перемене знака B_z-компоненты ММП, в первый момент вообще не может войти в магнитосферу, поскольку в ней еще остался градиент давления, соответствующий старому значению тока. Только через некоторое время, когда новая система конвекции перестроит давление, ток нового направления сможет войти в магнитосферу. Общее потребление энергии магнитосферой падает при северной ориентации ММП из-за резкого уменьшения стороннего тока через магнитосферу в первое время после обращения магнитного поля к северу и резкого уменьшения поля конвекции, тем большего, чем больше величина северного Bz. Затем постепенно плотность стороннего тока будет нарастать в течение 30–60 мин, но электрическое поле конвекции останется соответствующим текущему значению, поэтому магнитосферная активность в зоне полярных сияний и экваториальнее все равно останется на низком уровне. Из–за больших значений электрического поля в области антиконвекции, которая проецируется на полярную шапку, активность в последней будет, наоборот, повышена.

Если вертикальная Bz-компонента ММП имеет южное направление, то направление этого внешнего тока таково, что, замыкаясь через тело магнитосферы, он создает в ней силу Ампера, способную совершать работу по нагнетанию магнитосферной плазмы к Земле, в сторону увеличения магнитного и газового давления (рис. 6). В области, расположенной большей частью на 5<L<10 c ночной стороны, т. е. до максимума газового давления, находится МГД-компрессор. Сжатый им газ поступает в канал магнитосферного МГД-генератора, работа которого обсуждается. В отличие от области канала, область МГД-компрессора находится в районе, где плазма под действием магнитосферной конвекции движется почти радиально к Земле. Из баланса силы газового давления и силы Ам-

Тогда

„0      I Bc I p — q| ^71 [ J i+J в J, V cH )

где

(4y-1) ( LY’ q = 47 I Lt ) L-

Здесь Lc и LT – координаты конца и начала участка сжатия плазмы, Вс – напряженность магнитного поля на выходе компрессора. Далее мы будем считать, что Вс=В, т. е. выход МГД-компрессора территориально совпадает со входом МГД-генератора.

Поскольку плазме необходимо время на то, чтобы пройти от входа в компрессор до выхода,

^LcR dL

A T —  e—,

J V

LT R

то давление на входе в МГД-генератор будет соответствовать более раннему значению тока компрессора.

Интегрируя (16) по всей длине канала и полагая, что скорость плазмы на выходе много меньше скорости плазмы на входе МГД-генератора, найдем:

p

^^^^^^e

(Y+ 2) ( B

2Y

c

о * т V₀²

Подставив (18) в (19) с учетом сказанного о запаздывании, получим важное соотношение:

J i (t)- q^J i (t - ^AT)^—q^J в (t - ^AT)- J о (t).       ⁽²⁰⁾

В стационарном состоянии, когда нет явной зависимости от времени и q =1

JB=Jσ.                                             (21)

Рис. 6. Схема расположения функциональных блоков в геомагнитосфере: 1, 2 – вторичные МГД-генераторы, преобразующие энергию сжатого газа в электрический ток, питающий электроджеты в ионосфере; 3 – МГД-ком-прессор, преобразующий электрическую энергию в газовое давление; 4 – генератор во фронте головной ударной волны, преобразующий кинетическую энергию солнечного ветра в электромагнитную (при B_z<0).

пера следует

J i + J в — cH J B

' I dp I dL, I dL )

где В=В0/L³.

Это означает, что реально диссипативные процессы могут идти в магнитосфере только за счет внешнего источника тока и энергии. Все сложное магнитосферное «устройство» только перераспределяет токи и потоки энергии в пространстве и во времени. Это очевидное и ожидаемое заключение. Ценность (21) в данном случае заключается в том, что это уже не просто декларация. Можно указать, пределы применимости (21) и какие процессы стоят за понятиями «стационарность» или «нестационар-ность». Теперь обратимся к токам поперек хвоста. Обозначим J₁ + J_B через J_s. Тогда из (20) следует:

Js (t) = qJs (t - AT) + [ JB (t)- Ja (t)]. (22)

Очевидно, что управление током хвоста Js идет как за счет изменения JB, так и за счет изменения тока ионосферной нагрузки Ja. В квазистационарной ситуации, когда J–1dJ/dt <<1, q=1, имеем dJ s   [ J в - J a]

~ dt     AT

Очевидно, при J_B>J_a ток поперек хвоста растет и наблюдается вытяжение магнитосферного магнитного поля в хвост. Происходит вытяжение магнитного поля хвоста, и часть энергии запасается также в деформированном магнитном поле. При обратном соотношении, когда ток ионосферной нагрузки превышает внешний ток, dJs/dt<0 и ток хвоста падает, происходит диполизация магнитного поля. Физической причиной этого является увеличение ионосферного потребления тока из-за возрастания проводимости, обусловленного усилением высыпаний авроральных частиц. Таким образом, между потребителем тока и энергии и их «генеральным поставщиком» – внешним током – существует гибкая связь через «депо», которым является ток J1.

Хорошо известен эмпирический метода расчета полного потока энергии е, поступающего в магнитосферу [Akasofu, 1980]. При этом оказывается, что максимум потока энергии из солнечного ветра в магнитосферу е опережает ход АЕ-индекса, отражающего потери энергии в ионосфере. Как видно из рис. 7 (см. [Akasofu, 1980]), имеется такой интервал времени, в котором е уже падает, а АЕ-индекс еще растет. Этот факт получил трактовку в терминах «загрузка– разгрузка» энергии. По-видимому, имеется некоторое энергетическое депо, куда входящая энергия загружается и откуда она затем разгружается через магнитосферно-ионосферную токовую систему. В работах [Ponomarev et al., 2006a, b, c; Пономарев и др., 2009] было показано, что ток утро–вечер совершает работу над магнитосферной плазмой, сжимая ее при движении к Земле. Эта область называется МГД-компрес-сором. В области внутренней границы плазменного слоя, где газовое давление падает вдоль линии конвекции, расположена область МГД-генераторов. Эта область через электрические токи связана как с ионосферой, так и с МГД-компрессором. Таким образом, МГД-компрессор питается как внешним током, так и током МГД-генераторов, который оказался «невостребованным» ионосферой.

Рис. 7. График потока энергии из солнечного ветра в геомагнитосферу (так называемый параметр Акасофу) и график АЕ-индекса, который отражает потери энергии в ионосфере [Akasofu., 1980].

Когда во время возмущений ток ионосферной нагрузки увеличивается, суммарный ток поперек хвоста падает – происходит диполизация. Диполи-зация будет проявляться и тогда, когда падает внешний ток. В любом случае реакция МГД-генераторов на изменение тока через компрессор будет происходить с задержкой. Задержка эта вызвана тем, что плазменная трубка с увеличенным или уменьшенным давлением должна проделать путь со скоростью конвекции от компрессора до генератора, где газокинетическая энергия превращается в электрическую. Именно этот сдвиг фаз в работе компрессора и генератора создает ситуацию, когда входная мощность уже падает, а реализуемая еще растет.

II. В разделе I мы рассмотрели важный, но частный случай взаимодействия ионосферы с магнитосферой. При нахождении самосогласованного решения было получено и проанализировано решение в виде V=V0–γx/(γ+2)τ, однако существует еще одно решение вида V=V0exp{–f(x)}. Оно является довольно громоздким и с целью экономии места здесь не приводится. В случае экспоненциальной зависимости скорость на выходе из канала магнитосферного МГД-генератора уменьшается до ненулевого конечного значения. В рассмотренном выше случае территориальное совпадение токовой магнитосферной структуры с «ионосферной крышкой» было обеспечено в рамках постановки задачи. Но всегда ли это так? Всегда ли магнитосферные источники стыкуются с ионосферными потребителями электрической энергии «территориально»? Конечно, небольшая нестыковка не создаст больших проблем. Если под ионосферным потребителем, т. е. под областью повышенной ионизации и значительной напряженности электрического поля, не будет магнитосферного источника тока, то электрическое поле моментально «сядет» и эта область просто «выйдет из игры». Наоборот, если магнитосферный источник не найдет своего потребителя, должно произойти перераспределение газового давления в соответствии с требованиями отсутствия продольного тока, но в небольшой области. В этом случае к небольшой области можно применить представления однородности, использованные выше, при анализе течения в канале. Напомним, что там при уменьшении потребле- ния тока ионосферой происходит уменьшение градиента газового давления. Как было отмечено ранее, ток «подстраивается» дольше, чем электрическое поле. Это процесс достаточно медленный. Видимо, должен существовать и достаточно быстрый процесс запрещения или компенсации продольного тока со временем порядка баунс-периода. Вероятно, он тесно связан со структуризацией высыпаний частиц в ионосферу с образованием авроральных форм. Но этот вопрос выходит за рамки настоящего исследования.

Итак, имея пространственное распределение давления в функции координат и времени, можно рассчитать пространственное распределение объемных токов в магнитосфере:

j=c [BxVpg]/B 2. (24) Дивергенция j при стационарных условиях дает выражение для плотности продольных токов [Пономарев, 1985]

l j^ = cB, J{[Vpg xVpв]B / pвB3}dl. (25) 0

Интегрирование ведется по магнитной силовой линии дипольного поля Земли от экватора (0) до ионосферы (l). Подынтегральное выражение зависит от угла пересечения изолиний магнитного и газового давлений. В дипольном приближении изолинии pB=const – просто окружности. Наоборот, изолинии pg=const имеют сложную конфигурацию. Знак тока j в результате зависит от знака синуса угла между нормалями к изолиниям давления.

С другой стороны, можно рассчитать потоки высыпающихся электронов в ионосферу:

je=2.5B^I ∫pe dl/Bτ. (26)

В диапазоне энергий 1–20 кэВ на один акт ионизации приходится почти одно и то же количество энергии δε, в среднем примерно 30 эВ. Положим, что равновесное значение электронной концентрации в динамо-области ионосферы равно

Ne=(je/H^*δεα)^1/2, (27) здесь δε – количество энергии (эрг), je – плотность потока энергии (эрг/см²), α –коэффициент рекомбинации (см³с^–1), Н^* – толщина динамо-слоя (см).

Тогда интегральная педерсеновская проводимость

Σр=(e²Ne/Mi)∫νin/(ωiB²+νin²)dz, (28) где е – заряд электрона, Мi – масса иона, ωiB – ионная гирочастота, ν_in – частота столкновений ион– нейтрал. Интегрирование идет по всей толщине токонесущего слоя, т. е. от 100 до 120 км. Поскольку пространственная неоднородность распределения ионизации по широте намного превосходит неоднородность электрического поля, можно считать, что ∂Jθ/∂θ≈ Eθ∂Σ/∂θ.

Электрическое поле, общее для ионосферы и магнитосферы, проецируется в ионосферу по магнитным силовым линиям стандартным образом. Поверхностная плотность педерсеновских токов опре- деляется по формулам

Jλ=ΣpEλ, Jθ=ΣpE. (29) Плотность продольного тока из ионосферы в высоких широтах можно вычислить по формуле jr =[∂Jλ/∂λ+cosθJθ+sinθ∂Jθ/∂θ]/R0sinθ. (30)

С использованием уравнений (25) и (30) в работе [Sedykh et al., 2004] было констатировано достаточно хорошее согласование продольных токов, которые получаются из дивергенции ионосферных поверхностных токов исключительно из-за неоднородности ионосферной проводимости, с магнитосферными токами, которые получаются из-за несовпадения изолиний газового и магнитного давлений. Таким образом, был получен ответ на вопрос об общем соответствии системы продольных токов «из магнитосферы» и системы продольных токов «из ионосферы».

Заключение

Проблеме магнитосферно-ионосферного взаимодействия посвящено много исследований [Пономарев, 1985; Ляцкий, Мальцев, 1983; Мальцев, 1995; Lyatsky, Hamza, 2000], но в такой постановке задача никем до этого не решалась, и никому не удавалось найти самосогласованное решение задачи магнитосферно-ионосферного взаимодействия в области авроральных электроджетов. В данной работе приведено решение задачи сопряжения «градиентного» тока магнитосферы, зависящего от градиента давления плазмы, но не зависящего от электрического поля, с «резистивным» током ионосферы, зависящим от электрического поля, но не зависящим от газового давления. Это имеет большое значение не только для физики магнитосферы, но и для физики плазмы, поскольку решалась весьма интересная задача взаимодействия двух принципиально отличающихся по физике процессов областей с плазмой.

По крайней мере, два серьезных аргумента можно привести в пользу разработанной модели магнитосферно-ионосферного взаимодействия в области авроральных электроджетов. В самом деле, прототипы каналов, рассмотренных в данной работе, – плазменные коридоры – находятся в непосредственной близости от максимума газового давления на ночной стороне магнитосферы, т. е. максимума высыпаний частиц в ионосферу. Именно там располагаются электроджеты. Другой аргумент заключается в том, что конфигурация системы продольных токов в этом случае воспроизводит картину втекающих и вытекающих токов, которая была экспериментально установлена ранее [Iijima, Potemra, 1978].

Разрабатываемая проблема достаточно актуальна, поскольку магнитосфера, с одной стороны, является средой, через которую должны проходить воздействия, ответственные за солнечно-земные связи; с другой стороны, там во все большей степени отражается деятельность человека. Именно магнитосферные процессы оказывают существенное влияние на поведение высокоширотной ионосферы. Помимо познавательной ценности, такая разрабаты- ваемая модель магнитосферно-ионосферного взаимодействия будет полезна для предсказания реакции геомагнитосферы на экстремальные ситуации, отсутствующие в обучающей выборке эмпирических моделей, а также для сопряжения различных эмпирических моделей прогнозирования магнитосферноионосферных возмущений и определения границ их применений.

К сожалению, непосредственные наблюдения распределения плазмы в магнитосфере связаны с большими трудностями, потому что повсюду на ночной стороне магнитосферы надо знать плазменное давление с высоким разрешением, которое невозможно пока обеспечить имеющимися спутниками. Как показали авторы [Waters et al., 2001], для картографирования систем продольных токов с часовым разрешением необходимо иметь группу из 66 спутников (Iridium System). Многоспутниковые проекты активно развиваются и необходимы, однако проект с использованием данных от 66 спутников был бы очень дорогим проектом. Поэтому возникает необходимость в моделировании процессов в околоземном космическом пространстве, и важно только правильно выбирать исходную систему уравнений и далее корректно ее применять. Возможно, загадка суббури кроется в распределении плазмы на ночной стороне магнитосферы, а точнее, в перераспределении плазменного давления на ночной стороне магнитосферы при Bz ММП южного направления [Пономарев, 1985; Ponomarev, Sedykh, 2006c]. В первых работах Харелла, Вольфа и др. [Harell et al., 1981] имелись существенные недостатки в построении самосогласованной модели (см. критику данных работ в [Пономарев, 1985]), тем не менее, работы в данном направлении за рубежом продолжаются и в настоящее время [Wolf et al., 2009; Lyons et al., 2009].