Моделирование эффекта взаимного влияния микрополосковых элементов УКВ-дипазона

Большая часть работ в области изучения цифровых антенных решёток выполнена с использованием классической теории. Фундаментальным для этого подхода является предположение, что взаимное влияние (ВВ) между антенными элементами (АЭ) пренебрежимо мало. Во многих случаях это предположение оправдано. С другой стороны, в областях со строгими требованиями, ВВ должно учитываться при проектировании. Области, представляющие особый интерес, включают высокочувствительные антенны для медицинской техники, спутниковой связи, дистанционного зондирования и радиоастрономии [1].

Ключевыми причинами возникновения взаимного влияния можно считать следующие: недостаточная изоляция; снижение эффективности антенны; уменьшение коэффициента усиления антенны; высокая корреляция между излучателями [2].

Рассмотрим воздействие взаимного влияния относительно цифровых антенных решёток [3]. Решаемые задачи, направленные на достижение цели: провести моде- лирование антенных решёток с разными видами антенных элементов. Провести моделирование алгоритмов для антенных решёток с разными видами антенных элементов: диполями и патч-антеннами. Провести моделирование алгоритмов с учётом таких факторов, таких как S-параметры решётки и искажённые диаграммы направленности элементов.

Принцип работы цифровых антенных решёток

Существует достаточно большое количество алгоритмов оценки угловых координат радиосигналов для цифровых антенных решёток. Их целью является определение мощности сигнала на выходе АР в зависимости от угла прихода сигнала. По максимумам этой функции, называемой псевдоспектром, можно оценить, с какого направления поступает радиосигнал. Достаточно широко известны алгоритмы Барлетта, Кейпона, MUSIC и т.д.

На рисунке 1 представлена обобщённая схема процесса радиопеленгации цифровой антенной решётки. Её можно разделить на две части: аналоговую и цифро- вую. В аналоговой части происходит приём сигналов антенной решёткой. В цифровой части происходит расчёт сначала кор- реляционной матрицы, а затем и псевдо спектра.

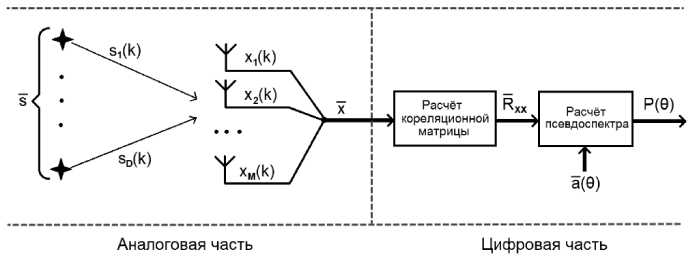
Рис. 1. Общая схема системы цифровой пеленгации

Далее рассматривается модель работы алгоритмов пеленгации в соответствии с данной схемой на рисунке 1. Пусть имеется линейная антенная решётка, состоящая из M антенных элементов. Она принимает D независимых сигналов из D разных направлений с углами θD, как показано на рисунке 1. Здесь SD(k) – падающий сигнал, xm(k) – принятый сигнал с M-го антенного элемента, y(k) – итоговый выходной сигнал. В итоге формула для матрицы выходного сигнала решётки имеет следующий вид:

x = A • s + n(1)

где n – матрица шума; A – матрица сканирующих векторов, рассчитываемая по следующей формуле:

A = [q(в,) q(0,) ■■■ q(0„)]

где q ( 0 ) — это сканирующий вектор из M элементов для направления 0:

q (0) = [1  ejsin 0 ■■■ e(M-1)п sin 0 ]

Здесь представлена формула для линейной решётки. Учитывается сдвиг фаз в антенных элементах, вызванный их расположением (с расстоянием между элементами в 0,5λ).

Корреляционную матрицу определяется по следующей формуле:

— ^ x ,⁽ к ) • x ,⁽ k ) *   •••   — £ x ,⁽ k ) • x M ⁽ k ) *

N k = 1                        N k = 1

R xx

NN

^ ^xM ^{( k} ) • x ,^{( k} )*  •••  — ^ ^xM ^{( k} ) • ^xM ^{( k} ) *

, N k = 1                           N k = 1

где N - число отсчётов цифрового сигнала, x_M ( k ) * - эрмитово-сопряжённая матрица.

Далее на основе корреляционной матрицы рассчитывается псевдоспектр. Ниже представлены формула для методов Барлетта [6], Кейпона [7, 8] и MUSIC [9] соответственно:

P B ( ^в ) = P C (^е) =

P MU ^(в ) =

а ( в ) ' у ( е )

а (в) HR- а (в)

I aH(в)ENENa(в)

где а (в) - матрица сканирующих векторов для всего диапазона пеленгации, E –собственный вектор шумов. Выражение (5) соответствует методу Барлетта, формула (6) – методу Кейпона. Метод MUSIC (7) несколько отличается от представленных выражений. В его формуле используется не корреляционная матрица (4), а вычисляемый на её основе собственный вектор шумов E . Подробнее математические преобразования рассмотрены в [1, 2].

Взаимное влияние и метод встроенных элементов (embedded elements)

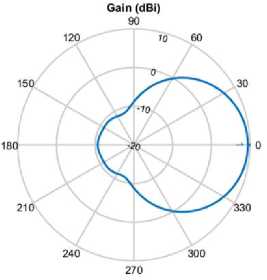
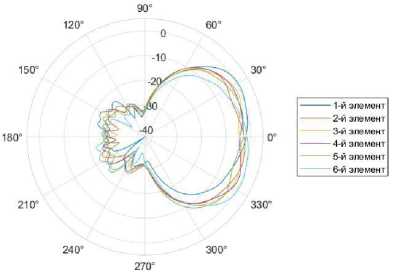
Одним из условий в классическом анализе антенных решёток является исключе- ние взаимной связи – предполагается, что ДН всех антенных элементов идентичны. Обычно в расчётах принимается ДН изолированного элемента. На рисунке 2а представлен пример подобной ДН. Такого рода приближение справедливо для антенных решёток с большим числом элементов. Однако для решётки с относительно небольшим количеством элементов взаимное влияние оказывает более сильное влияние и, как следствие, ВВ существенно ис- кажает диаграммы направленности отдельных элементов (рис. 2б). Следовательно, общая ДН решётки больше не является просто произведением коэффициента решётки и ДН изолированного элемента.

• а)                                          б)

Рис. 2. Диаграммы направленности патч-антенны

• а) изолированного антенного элемента, б) с учётом взаимного влияния

Для проведения более приближённых к реальности расчётов требуется вычисление диаграмм направленности для каждого отдельного элемента антенной решётки. Диаграмма направленности отдельного элемента с учётом взаимного влияния представляет собой ДН антенной решётки, в которой исследуемый элемент считается активным, а все остальные элементы являются пассивными с отключёнными выходами. Такой подход принято называть вычисление по методу встроенного эле- мента (embedded element). Ключевым моментом является то, что вычисленная таким образом ДН отдельно АЭ – это диаграмма направленности, учитывающая всю антенную решётку, включая рассеяние вблизи активного элемента.

Моделирование антенных решёток

Было проведено моделирование антенных решёток согласно методу моментов по методу встроенного элемента (рис. 2б). После расчёта каждого типа антенны вы- полнялась оптимизация для того, чтобы максимизировать коэффициент усиления (КУ) и минимизировать параметр S11 при импедансе, равном 50 Ом. Моделирование проводилось согласно следующим параметрам:

• -    количество элементов решётки M = 6;

• -    частота принимаемого сигнала – 5 ГГц.

Ниже представлены полученные модели и их характеристики.

Таблица 1. Параметры моделей антенных решёток

Номер модели	Внешний вид	Описание	Материал антенн	Материал диэлектрика
1		ЛАР, элементы – прямоугольные патч-антенны, элементы оптимизированы, КУ = 10 дБ, S11 = -21 дБ на f = 5 ГГц	идеальный проводник	воздух
2		ЛАР, элементы – прямоугольные патч-антенны, элементы оптимизированы, КУ= 1,8 дБ, S11 = -11 дБ на f = 5 ГГц	медь	FR4
3	-||>'-е^^^5^ 6         y                        ^^е	ЛАР, элементы – прямоугольные патч-антенны, элементы оптимизированы, КУ= 4,8 дБ, S11 = -17 дБ на f = 5 ГГц	медь	RO4730JXR

По результатам проведённых экспериментов было проведено сравнение нескольких антенных решёток с различными видами антенных элементов. Наилучшие результаты в значениях отклонений и минимально различимых углах показали линейные антенные решётки с элементами – полосковыми антеннами с воздушным диэлектриком (№1, Таблица 1). Значения параметров составили 4 дБ и 10-14° соответственно. Данный вид АЭ обладает самыми высокими значениями коэффициента усиления (рис. 3).

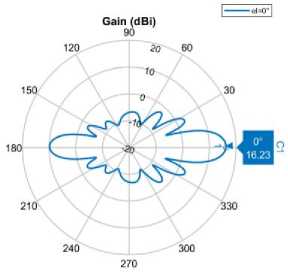
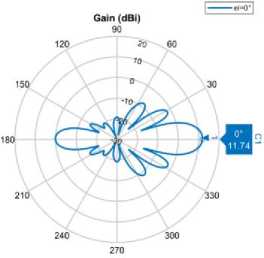
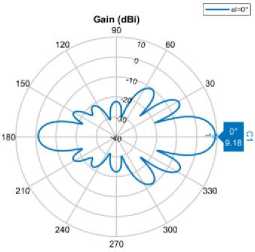
а) 16,23 дБ                 б) 11,74 дБ                  в) 9,18 дБ

Рис. 3. Сравнение коэффициента усиления главного лепестка ДН для АР с разными видами диэлектрика а) воздух, б) FR4, в) RO4730JXR

Более низкие результаты показали элементы с диэлектриком марки RO4730JXR (мощность появления отклонений 10 дБ, минимально различимые углы 20°). Ещё более низкие результаты показала АР с диэлектриком FR4 (20 дБ и 38°).

Разница в результатах между антенными решётками вызвана различиями в параметрах материалов диэлектриков. При моделировании использовались следующие материалы подложек:

• -    Воздух

• -    FR4 (простой стеклотекстолит)

• -    RO4730JXR (ламинат антенного класса)

Основными характеристиками материала подложки являются относительная диэлектрическая проницаемость ε r и тангенс угла диэлектрических потерь tgδ [3]. Значения данных параметров, использовавшиеся при моделировании, представлены в таблице 4.

Таблица 4. Параметры материалов диэлектриков АЭ

Название	Диэлектрическая проницаемость, ε r	Тангенс угла диэлектрических потерь, tgδ
Воздух	1	0
FR4	4.8	0.026
RO4730JXR	3	0.0023

Согласно [2], коэффициент усиления антенны уменьшается с увеличением тангенса угла потерь для всех частот. Потери мощности в диэлектрике увеличиваются с ростом частоты, а также при использовании материалов с высокими tgδ и εr (подробно данная зависимость рассмотрена в [4]). Согласно данным, представленным в таблице 4, значения tgδ и εr у FR4 выше, чем у RO4730JXR и воздуха, что является причиной более низких результатов ан- тенных решёток с данным типом диэлектрика.

В связи с этим, материалы, применимые в ВЧ-УВЧ диапазонах, при использовании в УКВ диапазоне показывают заметно меньшие результаты по сравнению с идеальным случаем (воздух) и специализированными материалами (RO4730JXR). Согласно [5], предпочтительными для использования в СВЧ технике являются материалы с ε r =2-10 и tgδ=10^-3-10^-4.

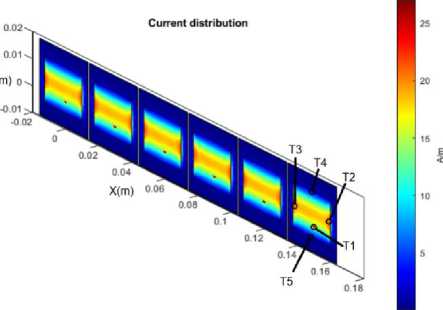
Рис. 4. Пример распределения поверхностного тока в АР

Рассмотрим, как распределяется ток в микрополосковом антенном элементе. Наибольшее значение наблюдается в точке крепления линии питания (точка Т1 на рис. 4). Высокие значения тока располагаются между правой и левой гранями излучателя (грани, параллельные оси Y на рис. 4), достигая максимума на самих гранях (точки Т2 и Т3). Меньшие значения тока наблюдаются на гранях, параллельных оси X (точки Т4 и Т5).

Рассмотрим, как эффект взаимного влияния проявляется в распределении поверхностных токов в антенных решётках. На рисунке 5 изображена антенная решётка №3 из таблицы 1 и график распределения тока.

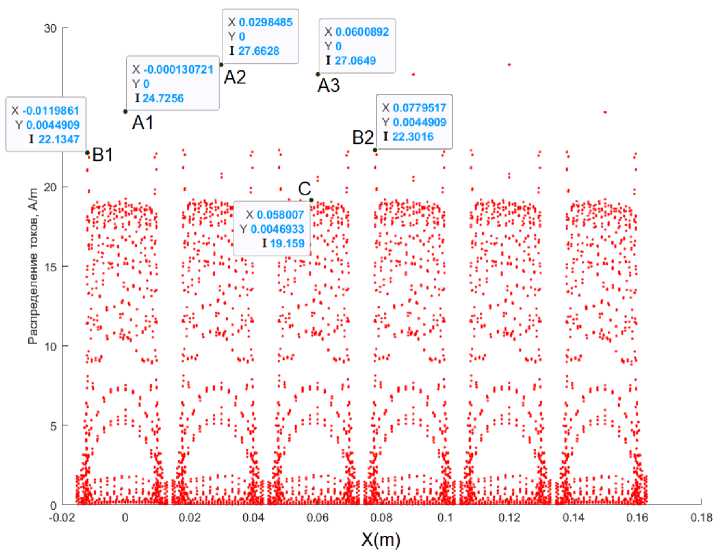
а) Значения тока в разных точках АР

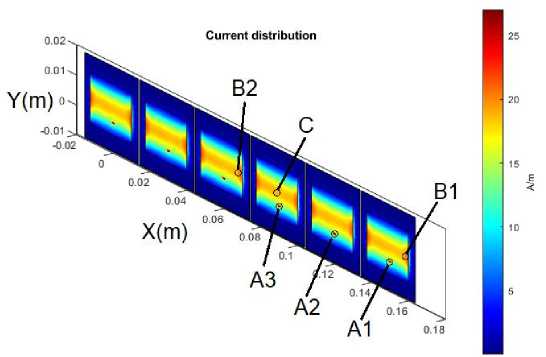
б) Расположение точек на АР

Рис. 5. Распределение токов в антенной решётке

Рассмотрим полученные данные. Значения тока в точках А1, А2 и А3 (места крепления линии питания) у 1, 2 и 3 элемента различаются между собой. Также отличаются токи в точках В1 и В2 (правый край излучателя) у 1 и 3 элементов. В целом видно, что распределение тока в каждом антенном элементе отличается. Важно отметить, что картина изменений в распределении токов симметрична между 1-3 и 4-6 антенными элементами. Это является проявлением воздействия эффекта взаимного влияния между элементами антенной решётки.

Самый низкий результат продемонстрировали решётки 2 и 3 из таблицы 1, где АЭ расположены плотно друг к другу и, следовательно, имеют наибольшее взаимное влияние. Они имеют одинаковую форму антенных элементов и отличаются только материалом изготовления.