Моделирование экспериментов по измерению поверхностного натяжения по форме поверхности капли при наличии несовершенств в ее подвесе или опоре

Введение ,, характеристику поверхностного слоя жидкостей и твердых тел на границе с различными фазами (              ,                            ,                                        ).,

,                                           .,-

,-

,                                                                                                                                  ,                                                                 ,-

,                                          ,.

-

:                                  (                                            ),-

,                                                                    ,                                                                                                                              .-

,.

их помощью в ряде случаев удается получить довольно точные и согласованные друг с другом

-.–

(                ,           ,               ) –                                                                                                            -,

, .-

..                     ..               : «...-

.- ных для настоящего справочника в большинстве случаев использовались сведения последних

» [1, . 331].                     ,-

., скажутся возможные несовершенства в проведении опытов на оценках величины поверхностного ..

Постановка задачи .-

,

.-

• ¹    Речкалов Виктор Григорьевич - кандидат педагогических наук, доцент, кафедра общей и теоретической физики, Южно-Уральский государственный университет.

• ²    Бескачко Валерий Петрович - про<|>ессор, доктор физико-математических наук, кафедра общей и теоретической физики, ЮжноУральский государственный университет.

ки, на которой она подвешена (для случая висящей капли). На практике державка имеет цилиндрическую форму и располагается в горизонтальной плоскости только приближенно, что нарушает цилиндрическую симметрию капли. Учет влияния указанных погрешностей на точность определения поверхностного натяжения приводит к необходимости расчета формы несимметричной капли.

Для решения этой задачи воспользуемся принципом минимума энергии: капля принимает такую форму, при которой она обладает минимумом потенциальной энергии при заданном объеме. Следовательно, в такой постановке рассматриваемая задача является задачей поиска условного экстремума.

Задача на поиск условного экстремума приводит к системе уравнений f дE .д V _ + X = 0 ‘ ^д xi      ^д Xi      ,

_ V = V где X - неизвестный вспомогательный коэффициент, E - энергия капли, V - ее объем, V0 - заданный объем, xi - независимый геометрический параметр, определяющий форму капли.

К сожалению уравнения данной системы нелинейные. Однако если имеется хорошее приближение для формы капли, то можно написать:

V = V ^{0} + 3 ^ 01

∂xi

A xi .

Здесь и далее по одноименным индексам предполагается суммирование. Индекс {0} означает, что величина рассчитывается по имеющемуся приближению для формы поверхности капли.

Используя формулу для полного дифференциала функции нескольких переменных, получаем :

дE   дE ^{0}   д² E ^{0}

=+

∂ x_i    ∂ x_i     ∂ x_i ∂ x_j

Ax j .

В результате приходим к следующей системе уравнений:

f д ² E ^{0}

∂ x_i ∂ x д V ^{0} ∂ xj

j

л , ^V ^{0} Δ x_j + λ

∂ x_i ∂ x _j

A xj = V ₀ - V ^{0}.

Δ xj =

д E ^{0}     . д V ^{0}

--X ------, ∂ x_i        ∂ x_i

К сожалению и эта система уравнений все еще не является линейной из-за неизвестного вспомогательного коэффициента X , который тоже должен быть определен. Рассматривая его наравне с другими переменными и считая известным некоторое начальное значение X 0, приходим к системе линейных уравнений, которую можно решить любым из известных методов:

ffд² E ^{0}   , 3² V ^{0}

------+ Л)-----

I д xi д xj      дxi дxj

д V ^{0}

Δ λ = ∂ x_i

д E ^{0}   „ д V ^{0}

--

∂ x_i

∂ x_i

A x, = V 0 - V ^{0}. ∂ xj

Будем искать решение методом последовательных приближений. При каждой итерации коэффициенты системы и свободные члены находятся по последнему найденному решению. Верхний индекс при этом принимает значение последнего найденного приближения. Поиск решения прекращается, когда разность значений некоторого контрольного параметра для двух соседних итераций не превышает заданной величины. В качестве такого параметра удобно использовать объем капли. Как показывает опыт, последовательность приближенных решений очень быстро сходится. Обычно достаточно от трех до пяти последовательных итераций, чтобы объемы отличались не более чем на 10-5 мм3.

Метод приближенного решения

При построении алгоритма решения удобнее считать, что решение ищется не для заданного объема, а для заданного веса. Вместо объема в этом случае мы должны будем подставить величину pgV, где р - плотность жидкости, g - ускорение свободного падения. Если после этого ка ждое уравнение поделить на рg, получим:

[ 1 д2 E . д2 V ) --+А)----- д V _    1 д E . д V

+—A A =---- А )—,

∂ x_i       ρg ∂ x_i     ∂ x_i

Д pg ^дх^дx    ^дxi^дxj)

— Ax• = V - V . д Xj   ^{j 0}

Верхние индексы в системе уравнений (1), обозначающие номер приближения, мы опустили. За нулевое приближение принимается форма осесимметричной капли, рассчитанная по ме тоду Адамса [2]. При этом точки поверхности капли, граничащие с твердой опорой, изменяются в соответствии с заданной формой державки.

Если форма сечения державки сильно отличается от круга, то поиск решения ведется постепенно путем плавной деформации опорно -го контура капли. На рис. 1 показана плавная деформация опорного сечения капли в процессе решения.

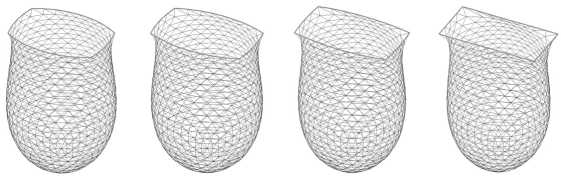
Рис. 1. Постепенная деформация опорного сечения капли к прямоугольному сечению

Для вычисления приближенных функций энергии капли (гравитаци- онной и поверхностной), а также объема капля разбивается на конечные элементы. Последние выбираются в виде пирамид (тетраэдров) с вершинами в начале координат (рис. 2). При этом на правления векторов ri считаем заданными. Форма капли, следовательно, будет зависеть только от расстояний r точек до начала координат. Это позволяет уменьшить количество неизвестных сразу в три раза.

Объем тетраэдра выражается как функция r :

rjx г - rjy г - rjz

rkx r = 6 rirjrk rkz

г0 rix riy

r )

⁰ rjx

⁰ r_jy r )

r )

0 rjy rz

=6 rirjrk ^A{ e ^}.

Верхний индекс в фигурных скобках обозначает номер конеч-ного элемента. Через ri°_т обозначены единичные направляющие векторы, a r - расстояния от вершин треугольников основания тетраэдров до начала координат. Определитель, составленный из координат направляющих векторов, является величиной постоянной в соответствии с нашим выбором способа задания поверхности капли. Верхний индекс {e} в обозначении объема и определителя означает номер конечного элемента.

Полный объем капли находится как сумма объемов отдельных элементов V = ^ V ^{ e ^}.

{ e }

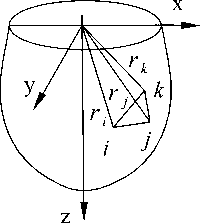
Рис. 2. Конечный элемент в виде тетраэдра

Определители, стоящие в правой части выражения для объема конечного элемента, вычисляются один раз по координатам точек нулевого приближения. В дальнейшем они считаются постоянными величинами, и мы имеем очень простое выражение для объема, как функцию произведений координат вершин треугольных элементов на поверхности капли.

DaATUUI/ W ГА I V ( ППМО •• ВЛ НТА К Я НТК 1^*1 ВЛ ЛУЛ I I М iz*l ГПЭПЛОМ I/O \Х .              «                      .                   .               »

Вычисление площади поверхности капли

Площадь поверхности конечно-элементной модели капли складывается из суммы площадей оснований тетраэдров. Площадь основания тетраэдра найдем из векторного произведения

^{5 {} e ^} = 1 ⁷ х /\

, где 7 1 = rj - ri и r ₂ = rk - ri .

^{5 {} e ^} = ^-( 7 — ri) ^{X (} rk — Г -)| = ^- | Г- 2^{1                               1} 2¹

^ri^{X r}j ^{+ r}j ^{X r}k ^{+ r}k ^X r j ,

- 0x,-0 -          -0x,-0 - X,-     -0x,-0

^ri^Xrj = ^ri^rj^ri ^Xrj , ^rj^Xrk = ^rj^rk^rj ^Xrk , ^rk^Xri = ^rk^ri^rk ^Xri .

Векторные произведения единичных направляющих векторов вычисляются один раз по ко -ординатам точек нулевого приближения, поэтому для них полезно ввести самостоятельное обозначение и рассматривать их как константы:

7 ⁰ X /j ⁰ = a , 7 0 X 7_k ⁰ = b , 70 X t] ⁰ = c .

Сумму векторов ri X rj + rj X rk + rk X / обозначим

A

A

.

Az

С учетом введенных обозначений можем записать

Ax = ^ri^rj^ax ^{+ r}j^rkbx ^{+ r}k^ri^Cx , Ax = ^ri^rj^ay ^{+ r}j^rkby ^{+ r}k^ri^Cy , Ax = ^ri^rj^az ^{+ r}j^rkbz ^{+ r}k^ri^Cz .

Выражение для площади боковой поверхности отдельного элемента и всей конечно -элементной модели капли:

5 ^{ e ^} =    /A ² + A 2 + A _z² , 5 = У 5 ^{ e ^} .

xyz

²                                   { e }

Поверхностная энергия капли, деленная на g g , равна

— Es = ^_ 5 = ^_ У 5 ^{ e ^} = У ^_ 5 ^{ e ^} = У c5 ^{ e ^},

Pg Pg Pg {e}       {e} Pg {e} где c - капиллярный коэффициент.

Гравитационная энергия капли

—Eg - — У PgV{e} zCe} = У V{e} z{ e ■ , Pg       Pg {e}                {e} где z{e} - вертикальная координата центра тяжести отдельного тетраэдра.

Для тетраэдра 7_с = -^-( r + rj + rk ), следовательно, zCe ^} = ^( г/ ⁰ + rjrj'z + rkr^z ).

Подставляя полученное ранее выражение для объема, получаем выражение для гравитационной энергии одного конечного элемента:

д{ e }

• V ^{ • ^{1 z {} e ¹ = 24 ' ⁷Гrjrkr ^{0 +} ri⁷⁰ v” z ⁺ rirjrk     ) .

xi системе уравнений (1) к переменным ri и вычислить все необходимые для решения системы коэффициенты .

Примеры расчетов

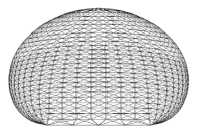
На рис. 3 приведены примеры расчетов формы капли, висящей на круглой и наклонной державке ( а ), на прямоугольной державке (б) и формы лежащей капли, опирающейся на прямоугольный контур ( в ).

а

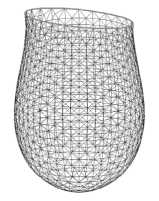
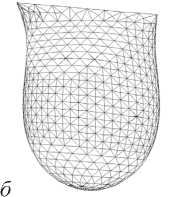
Рис. 3. Примеры расчетов

в

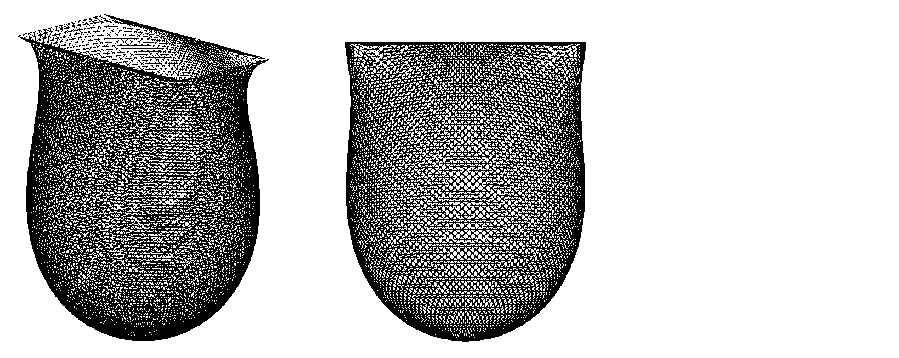
На рис. 4 приводится пример расчета с высоким разрешением, где поверхность разбивалась на 17 364 элемента 8 731 узлом.

Для капли, подвешенной на прямоугольном основании, была проведена экспериментальная проверка, которая показала хорошее соответствие расчетов с экспериментом.

Перспективное изображение

Вид на длинную сторону прямо -    Вид на короткую сторону прямоугольного основания              угольного основания

Рис. 4. Высокое разрешение

Моделирование процесса измерения поверхностного натяжения для случая несовершенства формы и ориентации державки капли

Координаты осевых сечений капли определялись при помощи программы «Форма», реализующей описанный выше метод расчета. Координаты находились для двух сечений, проведенных через минимальный и максимальный диаметры сечения державки. Затем по этим координатам по методике, описанной в [3], рассчитывалось поверхностное натяжение. Несовершенства формы капли приводят к появлению погрешностей в оценке поверхностного натяжения. Конечно , погрешности зависят и от размеров используемых конечных элементов. Меньшие элементы, позволяя получить большую точность, в то же время повышают вычислительную сложность и серьезно увеличивают время счета. В то же время, даже для самых мелких из использованных элементов количество точек на профиле капли получается значительно меньше того, что может быть получено в реальном эксперименте. Поэтому мы сравнивали полученные значения коэффициента поверхностного натяжения не с табличным значением для данной жидкости, а с тем значением , которое было получено при обработке расчетного профиля неискаженной капли, подве шенной на круглой горизонтальной державке.

На рис. 5 приведены результаты расчета по -грешностей в определении поверхностного натяже -ния, связанных с несовершенством формы держав -ки. Они получены для капли воды ( с = 72,8 мН/м), подвешенной на державке в форме эллипса с пара -метрами: большая полуось 1,681 мм, малая полуось 1,668 мм, эксцентриситет 0,1217 (такие параметры имела одна из державок в натурном эксперименте).

Из рис. 5 видно, что для данного капилляра погрешность измерения поверхностного

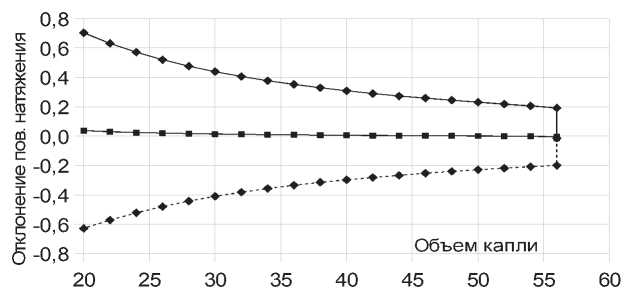
Рис. 5. Отклонение оценок поверхностного натяжения от «истинного» значения (в мН/м) в зависимости от объема капли (мм3). Верхняя кривая - значения, полученные обработкой профиля капли, проходящего через короткую ось опорного эллипса. Нижняя кривая - для профиля, проходящего через длинную ось эллипса. Кривая в центре - средние значения

натяжения, связанная с неточностью его изготовления, наиболее существенна для малых капель и

,.

,,

,

.

. 6-

,                                 ,                                        (                            1,4°).

.-

,.

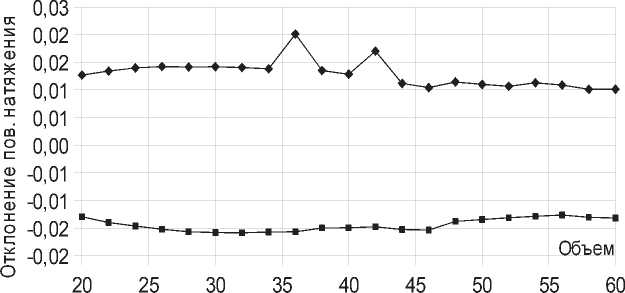
Рис. 6. Отклонение измеренного значения поверхностного натяжения от «истинного» значения (в мН/м) в зависимости от объема капли (мм3). Верхняя и нижняя кривые получены обработкой профилей капли, проходящих через короткую и длинную оси эллипса соответственно

,                  1,4°-

,                      ,                            ,                          0,02      / .,

.

Заключение

,-

.-

(            ,                                             ,                               )-

-

,.

,                                                                        ,-

,

,                                         (                                      )-

.                                  ,                                   ,,

,,

.