Моделирование экстремального наводнения в дельте дона на многопроцессорных вычислительных системах

23–24 марта 2013 г. в результате сильного штормового нагона воды из акватории Азовского моря значительная территория в дельте Дона чрезвычайно быстро была затоплена водой, в 20 населенных пунктах более 2,4 тыс. домовладений и свыше 5,3 тыс. человек оказались пострадавшими от наводнения. Материальные потери для населения и экономики региона оцениваются суммой более 500 млн. руб. Ветровая ситуация в период с 20 марта по 26 марта 2013 года складывалась таким образом, что ветер существенно менял направление и скорость: первую половину 23 марта дул ветер восточных направлений 3–11 м/с, к 19 часам направление ветров разворачивается на юг, усиливаясь до 5–12 м/с, после полуночи 24 марта ветра приняли западное направление со скоростью до 15 м/с. К 14–17 часам 24 марта порывы ветра достигали 20–22 м/с, что привело к очень быстрому затоплению прибрежных территорий, строений и объектов в населенных пунктах. Уровень воды поднимался со скоростью 11–12 см/час. К 18 часам 24 марта наблюдался максимальный уровень воды (280 см) по данным самописца, установленном на посту в п. Донской.

Ситуацию с затоплением усугубил повышенный (до 400 м3/с) попуск воды через гидроузел Цимлянского водохранилища в период с 21 по 25 марта, при этом дошедшая до низовьев Дона за двое суток волна половодья могла быть причиной дополнительного подпора вод, поступающих из Таганрогского залива.

По метеорологическим наблюдениям, полученным с береговой научноэкспедиционной базы Южного научного центра РАН на период с 20 марта по 26 марта 2013 года было промоделировано развитие нагонного явления в дельте Дона.

• 1.    Постановка задачи

При моделировании использовалась двухслойная математическая модель гидродинамики водоема, достаточно адекватно описывающая ветровые течения в Азовском море в целом, и в Таганрогском заливе в частности [3]. Данные водоемы имеют как относительно глубоководные районы, так и обширные районы мелководья.

Суть нашего подхода состоит в разбиении исходной трехмерной области расчета Ω (водной толще водоема) ограниченной сверху акваториальной, а снизу донной поверхностями на две — глубоководную и мелководную части. Для декомпозиции пространственной области моделирования Ω проведем горизонтальную секущую плоскость Р, отстоящую от невозмущенной поверхности водоема P0 на глубине, равной максимальной глубине мелководья (рис. 1). Таким образом плоскость Р разделила исходную область на две подобласти: верхний слой Ω1 (слой I) –все мелководье и верхняя часть глубоководного слоя, и глубоководный слой Ω2 (слой II). Предполагается, что эффект осушения из-за сгона воды может присутствовать только в мелководных районах.

Границы расчетной области Ω могут быть твердыми ∂Ω _T (донная поверхность, переходящая в береговую линию), участками втекания или вытекания воды ∂Ω _R , свободной поверхностью ∂Ω _S .

Считается, что на движение воды в слое I влияет ветер, а движение в слое II инициируется как градиентами давления, так и движением слоя I.

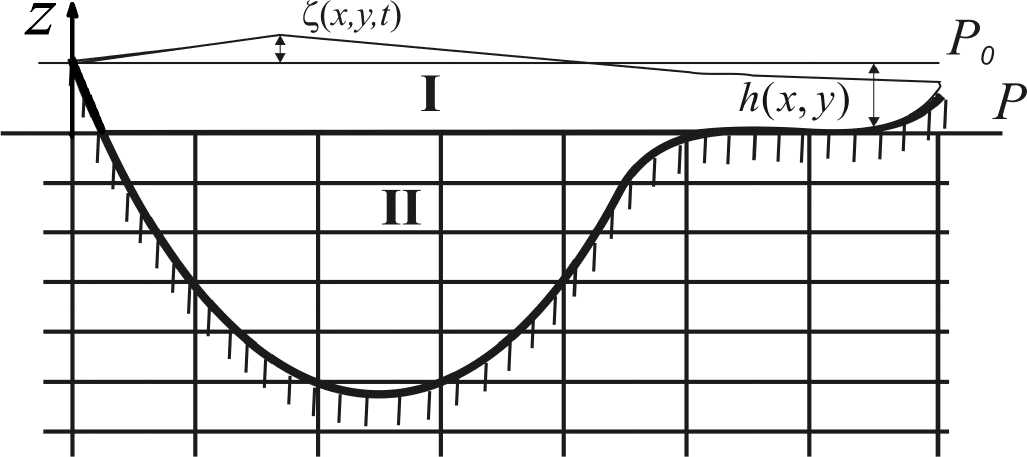
Рис. 1. Вертикальный разрез водоема с обширным мелководьем

Считаем, что слой I достаточно мелкий (значения возможных возмущений уровня воды и глубины слоя близки), а u и v не зависят от z. Движение воды в слое I описывается уравнениями мелкой воды:

du           dZ

• -    -Q v =- g^- + v dt s        d x     ^xy

dv          ⁹ Z

• -    + ^U s =^— g 7 ⁺ V xy dt            ay

2 d u s

_v d x ² (d x ²

d ² u + —г

S y ²

^d v s

+ .

Sy

. 2

dZ+ dt

+ ^T sx

H

+ ^

H dHu s

—

• - T bx- + F x ( x , y ) ,

τ

• -+ + F ⁽ x , y ) , H

dHv

+----- = 0.

^y

Здесь H = h + ^ ; h = h ( x , y ) - глубина мелководного слоя; u _s = u _s

( x , У , t ) , v s = v s ^{( x} , У , t )

• -    скорости в слое I; функции F x ( x , y ) и F _y ( x , y ) описывают взаимодействие верхнего и

• нижнего слоев между собой; Z = Z(x,У, t) — возмущение уровня воды; О -коэффициент Кориолиса; τsx ,τsy – проекции на оси OX и OY силы трения ветра о поверхность водоема; τbx ,τby – проекции на оси OX и OY силы трения жидкости о дно (или нижний слой воды). Эти величины зависят от скорости ветра WB{wx,Wy} и течения WT {us, vs} и опре-
• деляются так:

τ s =γ W B W B , τ _b =βW _T W _T

, где в(x, У) - коэффициент трения верхнего слоя жидкости о дно (или о глубоководный слой); γ – коэффициент трения ветра о слой I.

Движение воды в глубоководном слое II описывается системой, состоящей из уравнений количества движения, уравнения неразрывности среды и уравнения гидростатического давления:

ди    ди   ди    ди _

— + и — + v— + w --Qv =

St

дх

ду    дz

1 др t- + v, p дх

xy

д и д и

к д

—2 + —2 + д х ²    ду ² _у

+ ТГ z дz к

S v S v --+ u — дt    дх

S v    д v

+ v-- + w-- + Q u = ду    Sz

1 др

--Я- + V

Р 5 у

д v

ди | дz J’

'   д ² v ^

—- + —- + (д х ² ду ² J

д (

⁺ т1 ^V zT I ’

Sz (

Su  dvSw

— + — + — = 0. dx  dy

P = g P ^{(Z -} z ) ⁺ P a .

Здесь u = u(x, y, z, t), v = v(x, y, z, t), w = w(x, y, z, t) - компоненты вектора скорости; p(x, y, z, t) - давление; x, y, z, t - пространственные переменные и время соответственно; Pa = Pa (x, У) - атмосферное давление; vxy, Vz (z) - коэффициенты горизонтальной и вертикальной вязкости соответственно; р - плотность воды; g = 9,8 м/с2 - ускорение силы тяжести.

Граничные условия на твердой границе dQ T задаются условиями скольжения:

,d

V nL = 0’

= 0 , ∂Ω _T

d“T где Vn – нормальная составляющая вектора скорости, Vτ – касательная составляющая вектора скорости. В местах втекания или вытекания воды dQR задаются соответствующие значения скоростей u =u ,v = v ,u    = u ,v = v .

∂Ω R      1 ∂Ω R      1 s ∂Ω R      s1 s ∂Ω R

На границе между слоями ∂Ωl ставится условие равенства скоростей u =u v =v ∂Ωl       s, ∂Ωl

Функции F x ( x , y ) и F y (х , y ) , описывающие взаимодействие I и II слоя, задаются следующим образом:

F x ( x , y ) = uw, F , ( x , y ) = vw.

В качестве начальных данных можно задавать известное распределение скоростей и уровня воды

0  000  0  0

ut=0=u ,ust=0=us, vt=0=v ,vst=0=vs, wt=0 = w ,ζt=0=ζ или считать эти значения нулевыми.

Уравнения модели решаются конечно-разностными методами. Алгоритм вычисления параметров течения воды на (n+1)-м временном слое основан на том принципе, что каждое уравнение является «определяющим» для своего неизвестного. Все остальные переменные считаются известными и берутся с n-го слоя. При конечно-разностной аппроксимации уравнений количества движения используются неявные "противопотоко-вые" схемы. Перепад уровня воды и вертикальная компонента скорости определяются из разностных аналогов уравнений дифференциальных уравнений.

Для решения систем линейных алгебраических уравнений, возникающих при дискретизации исходных дифференциальных уравнений, использовалась библиотека параллельных подпрограмм Aztec. В этой библиотеке реализован набор итерационных методов Крылова для решения систем линейных алгебраических уравнений с разреженными матрицами. Распараллеливание выполнено в парадигме «распределенной памяти» с использованием коммуникационной библиотеки MPI. Такой подход не только ускоряет вычисления, но значительно снижает требования к объему оперативной памяти на вычислительных узлах. При увеличении размера сетки при дискретизации решаемой системы уравнений достаточно просто увеличить количество вычислительных узлов для решения задачи. Особенностью итерационных методов является многократное использование операции умножения матрицы на вектор. Профилирование программы показало, что на эту процедуру приходится более 50% всех вычислительных затрат [1]. Поэтому оптимизации параллельной версии этой подпрограммы для минимизации объемов пересылаемых данных было уделено большое внимание. Тем не менее, из-за большого удельного веса коммуникационных операций при работе с разреженными матрицами трудно рассчитывать на высокую степень масштабируемости этой процедуры и соответственно всей программы в целом. Кроме того, прямое тестирование подтвердило, что использование этих методов предъявляет повышенные требования к коммуникационной среде.

На задаче расчета течений было протестировано время счета на трех вычислительных системах [2]:

• 1)    на кластере IBMX с 2-х ядерными процессорами Intel Xeon 5160 и коммуникационной сетью DDR Infiniband;

• 2)    на кластере INFINI с процессорами Intel Pentium 4 3.4 Ггц и коммуникационной сетью SDR Infiniband;

• 3)    на рабочей станции QUAD с 4-х ядерным процессором Q6600 c тактовой частотой 2.4 Ггц и оперативной памятью 4Гбайт. Использовалась разностная сетка с максимальным числом неизвестных n=1700000. При тестировании расчет проводился для 200 временных шагов.

• 2.    Анализ результатов расчета

Как и следовало ожидать, наибольшее ускорение (Sp) прослеживается на кластере IBMX, с коммуникационной сетью DDR Infiniband (см. таблицу). Линейное ускорение на этой платформе сохраняется для числа узлов. В то время как, на кластере c одно- кратной скоростью Infiniband ускорение начинает отклоняться от линейного уже для n ≤4

^p . И совершенно неоправданным представляется запуск нескольких MPI процессов на многоядерных вычислительных узлах (рабочая станция QUAD).

Сравнение производительности различных вычислительных платформ на задаче расчета ветровых течений в Керченском проливе.

Np	INFIN I (с)	Sp	IBM X (с)	Sp	QUA D (с)	Sp
1	3896	1,0	3828	1,0	2740	1,0
2	2132	1,8	2015	1,9	2154	1,3
3	1542	2,5	1376	2,8	2865	0,95
4	1212	3,2	1066	3,6	2920	0,93
5	1029	3,8	881	4,3	-
6	903	4,3	758	5,1	-
7	802	4,9	681	5,6	-

Численное исследование показало, что при использовании технологии MPI на вычислительной системе QUAD с 4-х ядерным процессором производительность немного возрастает при подключении 2-го ядра, а затем падает при подключении последующих. В то время, как на системах с распределенной памятью INFINI и IBMX наблюдается хороший рост ускорения при увеличении числа вычислительных узлов. Заметим, что на вычислительном кластере IBMX с 2-ядерным процессором на каждом узле запускался только один счетный процесс. Использование второго ядра, на малом числе узлов приводило к небольшому ускорению работы программы, а при увеличении числа узлов так же, как и на системе QUAD к замедлению работы программы.

Качество алгоритма оценивается совпадением расчетных значений с натурными данными, полученными на метеопосту в п. Донской (рис. 2).

Расчет проводился c шагом по времени dt = 5 минут, и данные снимались через каждые 3 часа. Видно, что модель достаточно хорошо описывает развитие гидрологической ситуации в данном районе.

Для расчета объема поступающей в дельту Дона воды (куб.м/с) из Таганрогского залива было рассмотрено поперечное сечение восточной части залива длиной около 30 км. Считалось, что на затопление расходуется только нагонная составляющая перепада уровня, которая с учетом скорости течения давала объемный расход поступающей воды.

На рис. 3 приведен график изменения объема поступающей из Таганрогского залива воды в дельту Дона.

Видно, что максимальный объем воды поступал в ночь с 23 на 24 марта и составил около 10 тыс. куб. м в секунду. Затем поступление стало резко уменьшаться, но все равно скорость поступления воды оставалось положительной, что вело к продолжению процесса затопления. И только к вечеру 24 марта поступление воды прекратилось, и во- да стала убывать. Вечером 25 марта расход убывающей в Таганрогский залив воды составил примерно 5 тыс. куб.м/с.

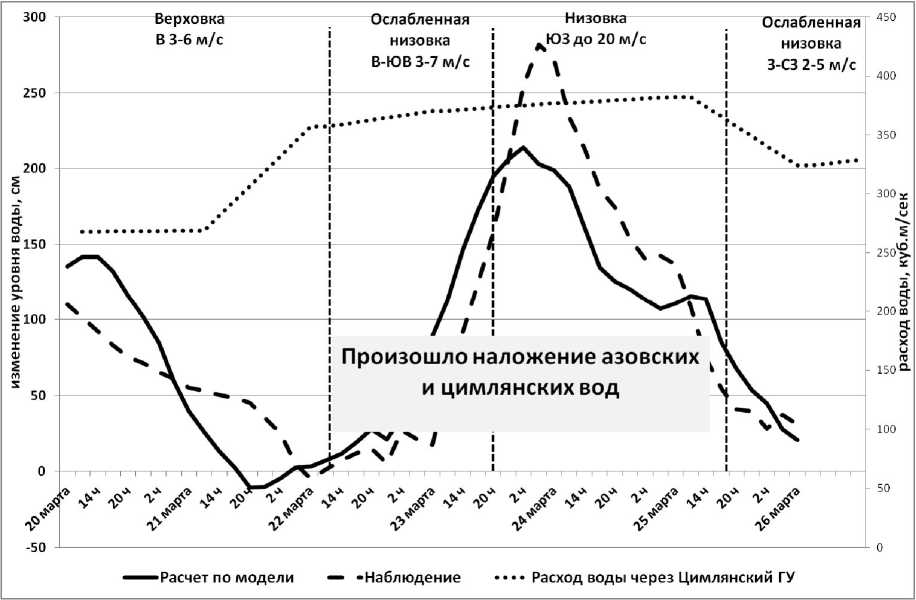
Рис. 2. Изменение относительного уровня воды на период с 20 по 26 марта 2013 года на посту «Кагальник»

С помощью моделирования установлено, что резкая смена сгонного эффекта на нагонный увеличивает скорость поступления воды, а, следовательно, и степень затопления дельты. Сравнивались две ситуации:

• а)    начало нагона при юго-западном ветре после штилевой погоды и

• б)    начало нагона после сгонного явления, то есть после действия восточного ветра. Сгон моделировался при скорости восточного ветра 9 м/с, который затем изменялся на ветер юго-западного направления скоростью 15 м/с.

В случае предварительного сгона значительно увеличивается скорость нагонного течения, а соответственно, и объем поступающей в дельту воды. Хотя в обоих случаях затопление дельты длился 22–23 часа, что соответствует динамике повышения уровня 23– 24 марта, изменения уровня воды существенно различаются. Если нагон начинается при штилевой погоде, то уровень воды поднимается от нулевой отметки, соответствующей естественной глубине водоема (рис. 4), и дальше монотонно возрастает по мере поступления излишков воды. Если перед нагоном наблюдался сгон воды, то сначала уровень отрицателен (что характерно для сгонного явления), но затем быстро увеличивается и, в конце концов, становится выше нагона после штиля. Этот результат показывает, что при резкой смене восточного ветра на западный затопление происходит быстрее и оно сильнее по масштабу, чем при постоянно действующим западном ветре.

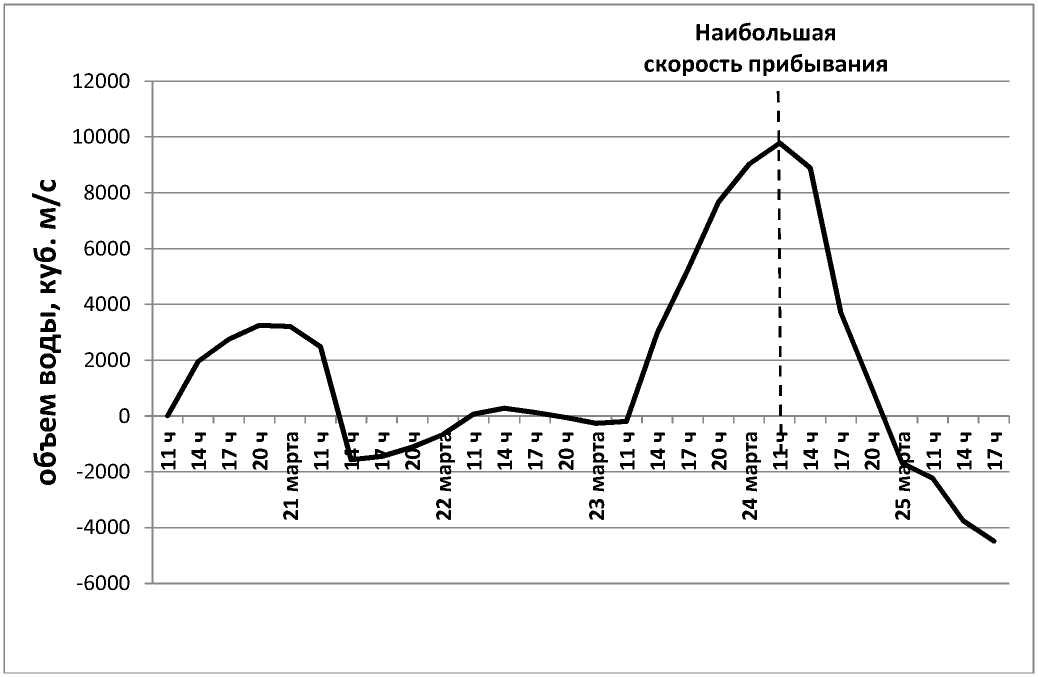
Рис. 3. Изменение объемного расхода воды на период с 20 по 26 марта 2013 года

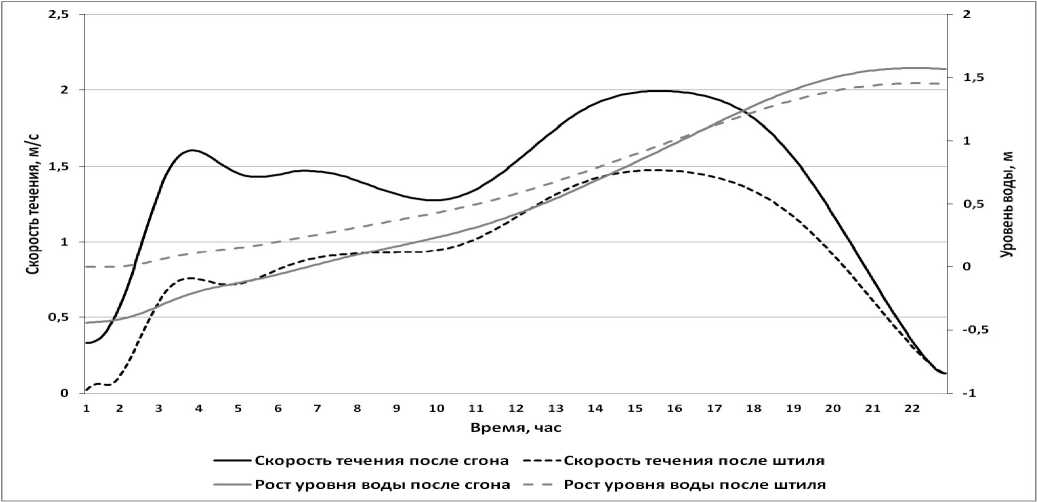
Рис. 4 . Поведение скорости течения и уровня воды при различных начальных условиях нагона

Заключение

Сравнение результатов расчета с наблюденными данными показало, что представленная математическая модель достаточно адекватно описывает гидродинамику течений в северо-восточной части Таганрогского залива, а также сгонно-нагонные явления. Данная модель позволяет рассчитывать ветровые течения и сгоны-нагоны в случае изменения береговой линии, что позволит в дальнейшем прогнозировать степень опасности затопления дельты Дона.