Моделирование электродинамических параметров микроволнового стерилизатора
Автор: Байбурин В.Б., Комаров В.В., Мещанов В.П.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 4 т.25, 2022 года.
Бесплатный доступ
Для стерилизации медицинских инструментов анализируется технология их иммерсионной термообработки интенсивным СВЧ-излучением на частоте 2,45 ГГц. Показаны преимущества данной технологии по сравнению с традиционными методами. Построена электродинамическая модель микроволнового стерилизатора хирургических инструментов, учитывающая зависимость комплексной диэлектрической проницаемости иммерсионной среды (воды) от температуры. В качестве его базового элемента был использован прямоугольный резонатор с волноводным элементом возбуждения. С помощью численной модели на методе конечных элементов определены величины отраженной и поглощенной мощности, а также темп нагрева воды в стерилизаторе для рабочей мощности 600 Вт. Анализ тепловых процессов, выполненный по упрощенной методике, показал достаточно высокую эффективность такого устройства, обеспечивающего высокий темп нагрева на заданной частоте.
Электромагнитное поле, свч-излучение, стерилизация, медицинские инструменты, математическое моделирование
Короткий адрес: https://sciup.org/140297119
IDR: 140297119 | УДК: 621.372.8:621.365.5 | DOI: 10.18469/1810-3189.2022.25.4.52-58
Текст научной статьи Моделирование электродинамических параметров микроволнового стерилизатора
Процессы высокотемпературного воздействия энергией электромагнитных (ЭМ) волн на различные объекты лежат в основе не только терапевтических, но и некоторых вспомогательных медицинских технологий. Одним из примеров таких вспомогательных технологий является стерилизация медицинских инструментов, которая чаще всего проводится путем либо их кипячения в воде традиционными методами, либо обработки горячим воздухом или специальными химическими веществами, что бывает не всегда удобно. При этом продолжительность стерилизации инструментов может оказаться значительной: горячим воздухом – до нескольких десятков минут, в автоклаве при давлении 0,8...3,5 Бар – порядка 15 мин. В ряде случаев, когда важнейшим фактором успешного хирургического вмешательства становится время, ускорить процесс стерилизации позволяет использование для этих целей высокоинтенсивного микроволнового излучения.
Для микроволновых технологий подобного типа выделены специальные частоты: 915 МГц, 2,45 ГГц, 5,8 ГГц, 24,125 ГГц, получившие название ISM-частоты (industrial, scientific, medicine). Как известно [1], интенсивность СВЧ-нагрева прямо пропорциональна частоте излучения, но с увеличением частоты снижается глубина проникно- вения ЭМ-поля в диэлектрик с потерями. Чаще всего в системах микроволновой термообработки встречается частота 2,45 ГГц, обеспечивающая необходимый компромисс.
Процессы микроволновой стерилизации медицинских инструментов существенно отличаются от аналогичных процессов тепловой обработки в области пищевых технологий, где нагрев образцов пищевых изделий осуществляется при температуре 121,2 ° , которая необходима для уничтожения одной из самых опасных бактерий типа Salmonella [2].
В данной работе рассматривается технология высокоинтенсивного воздействия ЭМ-излучения с частотой 2,45 ГГц на медицинские инструменты, погруженные в иммерсионную среду, в качестве которой используется обычная водопроводная вода.
1. Постановка задачи
В качестве базовых элементов микроволновых стерилизаторов чаще всего предлагаются [3–5] прямоугольные резонаторные СВЧ-камеры со стоячей волной, возбуждаемые стандартным прямоугольным волноводом WR340 с размерами поперечного сечения a × b = x × y = 86 × 43 мм и рабочей частотой 2,45 ГГц. Рассмотрим аналогичную конфигурацию микроволнового стерилизатора,
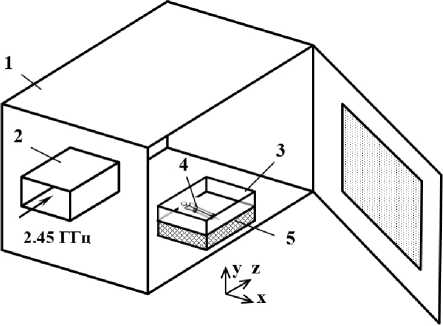
Рис. 1. Модель микроволнового стерилизатора: прямоугольный резонатор (1), волновод (2), контейнер с водой (3), медицинский инструмент (4) и подставка (5)
Fig. 1. Microwave sterilizer model: rectangular resonator (1), waveguide (2), water container (3), medical instrument (4) and stand (5)
внутри которого, как показано на рис. 1, на специальной диэлектрической подставке располагается контейнер с инструментами, заполненный обычной водопроводной водой. Контейнер и поставка выполняются из радиопрозрачного материала, например PTFE. Медицинские инструменты представляют собой конфигурационно сложные металлические объекты (рис. 2), количество которых в контейнере может быть произвольным.
Распределение ЭМ-полей в резонаторной камере с объемно-неоднородным диссипативным заполнением в общем виде описывается системой уравнений Максвелла:
-
- - d D -
- rot H = Q eE + — + Jcm,
dT
- rot E = - —, дт, div D = р + р cm,
- div B = 0, где E и H - векторы напряженности электрического и магнитного полей; D и B - векторы электрической и магнитной индукции; ое - электропроводность среды; Jcm - плотность стороннего тока; р - удельная плотность заряда; рcm - удельная плотность стороннего заряда. Все параметры, входящие в уравнения (1)–(4), в общем виде являются функцией координат и времени: Е(-, т), —* —* —* —*
H ( - , т ), D ( - , т ), В ( - , т ), J ( - , т ), р ( - , т ), р ( - , т ).
ñò ñò
Здесь - - радиус-вектор точки трехмерного про странства; т - время.
Свойства воды как диссипативной среды по отношению к ЭМ-полю определяются комплексной диэлектрической проницаемостью (КДП) Б = б' - j б" (здесь б' - диэлектрическая прони-
Рис. 2. Хирургические инструменты
Fig. 2. Surgical instruments
цаемость, б" - коэффициент диэлектрических потерь) и комплексной магнитной проницаемостью ц = ц'- j ц" ( ц' - магнитная проницаемость, ц" - коэффициент магнитных потерь), а также электропроводностью.
Принимая во внимание тот факт, что магнитные свойства воды ( ц' = 1, ц" = 0) не оказывают влияния на процессы рассеяния и поглощения ЭМ-волн внутри резонатора, а КДП воды на фиксированной частоте зависит только от температуры ( Т ), перепишем уравнения Максвелла с использованием метода комплексных амплитуд [6]:
rot H = j юБ( T )б0 E + J cm, rot E = - jtoPoH, div Бо б'( T) E = р cm, div H = 0, где б0 = 8,85 ■ 1О-12 Ф/м, цо = 1,257 ■ 1О-6 Г/м, E и H - комплексные амплитуды электрического и магнитного полей в заданной точке пространства: Е(т) = Re(Eejшт); H(т) = Re(Hе;'шт).
На частоте 2,45 ГГц диэлектрические свойства воды являются функцией температуры, и в интервале 0 < Т ° С < 1ОО их можно оценить с помощью соотношений, полученных в [7]:
б' ( T ) = - 4,6 ■ 10 - 6 T 3 +
+ о, 00131Т2 - о, 414T + 88,15, б"T) = -5 ■ 10-5 T3 + 0,О1О3T2 -
, (10)
- о, 8064 T + 26,675.
Используя подход, описанный в [8; 9], преобразуем уравнения (5)–(8) в уравнение Гельмгольца для термопараметрических сред:
E
I
V 2 d ? + к 2 Б ( T ) d ? + grad 7-^—, grad б' ( T ) =
Б ( T ),
t 1 jf divJcm I =1 ™ц о J cm - to o; grad . T J ,
где кО = to2Б;ц; - волновое число свободного пространства.
В случае Jст = 0 уравнение (11) преобразуется в хорошо известное из литературы [10] однородное уравнение Гельмгольца для сред, свойства которых зависят от Т °С:
Ц t ( T ) = v t ( T ) p t ( T ),
V 2 E + к 2 б ( T ) E + grad
E
——, grad s ( T )
= 0
где p t - плотность вещества.
Анализ вариаций этого параметра для воды [12]: 0,282 ■ 10 - 3 <ц t , Па-с < 1,52 ■ 10 - 3 - в интервале температур 0 < Т ° С < 100 показывает, что
высокие скорости гидродинамических потоков
Решения этого уравнения должны удовлетворять граничным условиям на металлических стенках:
E t = 0, d E n 1 d n = 0, (13) где E n и I S t - нормальная и тангенциальная компоненты напряженности электрического поля, а и на границе раздела сред при неоднородном заполнении СВЧ-камеры должно выполняться условие
E ii = E ii + 1 , (14) где i – номер среды заполнения.
На входе стерилизатора должен быть задан источник ЭМ-поля в виде
E (1) = M 11 exp( / Ри z ) + 5 11 M 11 exp( - j Ри z ), (15) где М 11 – собственные функции ЭМ-волны, распространяющейся в ПрВ; S 11 – коэффициент отражения; вц - фазовая постоянная ЭМ-волны на входе камеры. Для основной волны Н10 ПрВ:
M 11 = E 0 sin (—j , (16) где а – размер широкой стенки входного волновода, E i 0 - максимальное значение амплитуды поля в поперечном сечении волновода.
2. Анализ тепловых процессов
Общепринятый подход к анализу процессов взаимодействия ЭМ-волн с диссипативными средами связан с решением так называемой связанной краевой задачи электродинамики и тепло-массопереноса для термопараметрических сред, алгоритм которого хорошо известен [11]. В случае СВЧ-термообработки жидких сред формулировка такой задачи включает в себя уже не уравнение теплопроводности, а уравнение энергии и уравнения гидродинамики, учитывающие потоки жидкой среды внутри нагреваемого объема под действием тепловых источников [9].
Важнейшим параметром, оказывающим влияние на формирование теплового поля в области взаимодействия ЭМ-поля с жидкими средами, оказывается кинематическая вязкость ( v t ), входящая в дифференциальные уравнения гидродинамики, которая связана с динамической вязкостью ( ц t ) как [12]:
внутри жидкости приводят к практически мгновенному выравниваю температуры по всему объему. То есть в случае интенсивного воздействия СВЧ-излучения на воду можно пренебречь градиентами температур в области взаимодействия. Это, в свою очередь, позволяет ограничиться рассмотрением только электродинамической части связанной задачи, осуществляя оценку тепловых процессов в зоне нагрева по упрощенной методике [13], согласно которой темп нагрева
T ( т ) =
q v ( T ) C t ( T ) Р t ( T )
т + T 0 ,
q v = 0, 5 ®s0s" ( T ) Ei 2,
где Ct – теплоемкость воды, qv – плотность тепловых источников, Т 0 – начальная температура.
При этом для расчета qv можно использовать методы теории диссипативных СВЧ-многополюсников:
P ï q v V ’
P = ( 1 - 5 21 ) P 0 ,
где Рп – поглощенная СВЧ-мощность, Р 0 – входная (рабочая) мощность, V – объем нагреваемой жидкости, S 11 – коэффициент отражения.
Плотность воды при ее нагреве от 20
°
С до 100
°
С лежит в пределах: 958,4
t
, кг/м3
<
998,2, а теплоемкость - 4,18
<
C
t
, кДж/(кг^К)
<
4,22 [12], поэтому в первом приближении мы можем использовать их усредненные значения:
p
t
= =
978,3 кг/м3 и
C
t
=
4,2 кДж/(кг-К).
3. Численное моделирование Для численной реализации электродинамической модели микроволнового стерилизатора в данной работе были использованы метод конечных элементов (МКЭ) и пакет программ на его основе COMSOL V.5.2.
Геометрическая модель стерилизатора включает в себя прямоугольный резонатор размером
x
× ×
y
×
z
= 30 × 19 × 30 см с элементом возбуждения в виде волновода WR340, расположенным в центре боковой стенки резонатора, как показано на рис. 1. В центре резонатора на высоте 25 мм от нижней стенки на специальной подставке из PTFE разме-
Рис. 3.
Распределение электрического поля в вертикальной плоскости симметрии
yz
стерилизатора на частоте 2,45 ГГц
Fig. 3.
Distribution of the electric field in the vertical plane of symmetry
yz
of the sterilizer at a frequency of 2,45 GHz
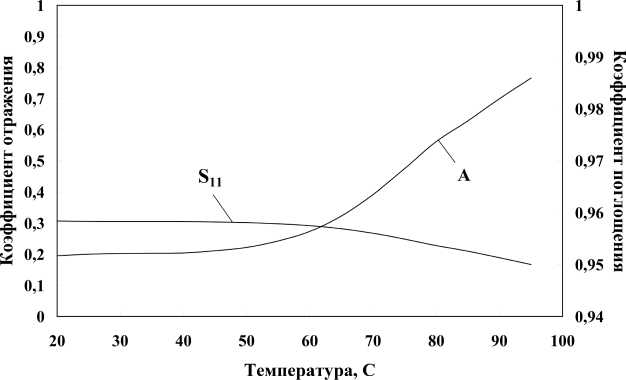
Рис. 4.
Электродинамические характеристики стерилизатора
Fig. 4.
Electrodynamic characteristics of the sterilizer
щается кювета с водой размером
x
×
y
×
z
= 150 × × 30 × 200 мм, нагрев которой осуществляется СВЧ-излучением с частотой 2,45 ГГц мощностью 600 Вт. Влияние толщины стенок кюветы не учитывалось, чтобы снизить вычислительные затраты [14].
Сеточная 3D-модель всей электродинамической системы включала в себя более 4·104 тетраэдрических векторных элементов Уитни первого порядка. Плотность сетки в зоне взаимодействия задавалась выше, чем в остальных областях резонатора. На входе волновода задавались условия распространения волны Н10 ПрВ и основные параметры СВЧ-сигнала. Численная полноволновая модель была дополнена функциональными зависимостями (9) и (10) для термопараметрической среды, и были найдены распределения ЭМ-поля в объеме стерилизатора. На рис. 3 показана структура электрического поля в резонаторе на рабочей частоте стерилизатора для температуры иммерсионной среды 95 °С. Да- лее были установлены значения коэффициента отражения и коэффициента поглощения (А), причем A = (1 - S121). (22)
Температурные зависимости этих двух параметров на частоте 2,45 ГГц приведены на рис. 4. Из этих данных видно, что с ростом
Т
°
С отраженная мощность плавно снижается почти в два раза, а поглощаемая мощность минимальная величина которой составляет
Рп
= 543 Вт при комнатной температуре 20
°
С, плавно возрастает примерно в 1,06 раза и достигает величины 578 Вт. Интересно отметить, что этот эффект наблюдается, несмотря на уменьшение параметра в"(
Т
).
Расчет темпа нагрева по упрощенной методике с учетом вариаций диэлектрических свойств воды от температуры показал квазилинейную зависимость
Т
(
т
). При этом рабочая температура 100
°
С достигается менее чем за 9 минут.
Заключение Таким образом, с помощью электродинамической модели (12)–(16) и методики приближенной оценки тепловых процессов в области взаимодействия были установлены эксплуатационные характеристики микроволнового стерилизатора медицинских инструментов с рабочей частотой 2,45 ГГц. Конечно-элементное моделирование стерилизатора на базе прямоугольного резонатора с волноводным элементом возбуждения и объемно-неоднородным диссипативным заполнением показало приемлемый уровень согласования источника с нагрузкой на уровне 5И < 0,31, то есть менее 10 % отраженной мощности. Кроме того, было найдено, что при объеме кюветы с водой V = 900 см3, которая используется в качестве иммерсионной среды для нагрева инструментов, темп нагрева составляет примерно 10 °С в минуту при входной мощности 600 Вт, что позволяет нагреть воду до 100 °С менее чем за 9 мин. Здесь необходимо отметить, что при заполнении кюветы медицинскими инструментами объем иммерсионной среды уменьшается и в реальных условиях будет достигнут более высокий темп нагрева. Для интенсификации таких процессов и повышения эффективности микроволновой стерилизации в качестве иммерсионной среды могут быть использованы солевые растворы различной концентрации. Однако при этом возможно увеличение такого параметра, как вязкость, и для оценки тепловых процессов в области взаимодействия необходимо решать более сложную связанную краевую задачу [9]. Работа выполнена при финансовой поддержке гранта Российского научного фонда (проект № 22-19-00357).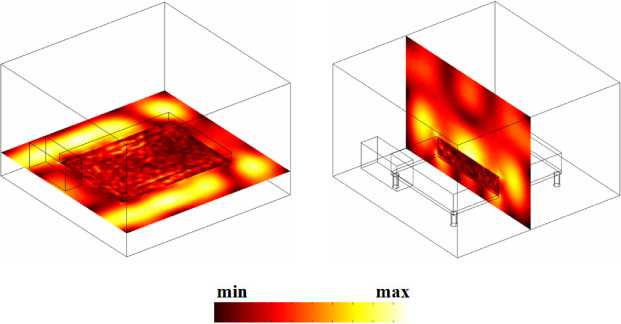
Список литературы Моделирование электродинамических параметров микроволнового стерилизатора
- Metaxas A.C., Meredith R.J. Industrial Microwave Heating. London: Peter Peregrinus, 1983. 356 p.
- Decareau R.V. Microwaves in the Food Processing Industry. New York: Academic Press, 1985. 236 p.
- Patent 5858303 US. Method and system for simultaneous microwave sterilization of multiple medical instruments / Schiffmann R.F., Held J.S.; priority 12.01.1999. 23 p.
- Патент на полезную модель 2004136734/22 (45271). Устройство сверхбыстрой стерилизации медицинских инструментов / Байбурин В.Б., Тертышник В.В., Шуб Г.М., Волков Ю.П., Капрелов Р.И.; приоритет от 14.12.2004. 5 с.
- Патент на полезную модель 2013122446/15 (136718). Устройство для стерилизации медицинских инструментов / Байбурин В.Б., Тертышник В.В.; приоритет от 15.05.2013. 3 с.
- Баскаков С.И. Электродинамика и распространение радиоволн. М.: Либроком, 2012. 416 с.
- Ratanadecho P., Aoki K., Akahori M. The characteristics of microwave melting of frozen packed beds using a rectangular waveguide // IEEE Transactions on Microwave Theory and Techniques. 2002. Vol. 50, no. 6. P. 1495–1502. DOI: https://doi.org/10.1109/TMTT.2002.1006410
- Гагарина Л.Г., Холод И.С., Бондаренко С.М. Модель процесса управления микроволновым нагревом // Известия вузов. Электроника. 2003. № 5. С. 94–95.
- Комаров В.В. Исследование процессов СВЧ-нагрева диссипативных сред с учетом конвективного теплообмена: теория и эксперимент // Прикладная физика. 2006. № 4. С. 34–40.
- Analysis of microwave heating of materials with temperature-dependent properties / K.G. Ayappa [et al.] // AIChE Journal. 1991. Vol. 37, no. 3. P. 313–321. DOI: https://doi.org/10.1002/aic.690370302
- Захаров В.В., Тригорлый С.В. Математическое моделирование СВЧ термообработки диэлектриков с учетом изменения их физических свойств // Вопросы электротехнологии. 2020. № 3. С. 5–12.
- Теплотехника / под ред. В.Н. Луканина. М.: Высшая школа, 2002. 671 с.
- Комаров В.В. Погрешность линеаризации решения совместной краевой задачи электродинамики и теплопроводности для некоторых диссипативных диэлектриков // Радиотехника. 2006. № 12. С. 78–82.
- Комаров В.В. Снижение вычислительных затрат компьютерного моделирования устройств микроволновой обработки материалов // Наукоемкие технологии. 2008. № 8. C. 45–49.


