Моделирование электрофизических процессов в сильноточных катодных узлах генераторов низкотемпературной плазмы

В настоящее время актуальной проблемой является повышение работоспособности и ресурса катодных систем, функционирующих в экстремальных условиях. В мощных плазменных установках токовая нагрузка внутри катодного узла становится решающим фактором функционирования и ресурса конструкции.

Следует отметить, что экспериментальная оптимизация катодных систем является достаточно трудоемким и дорогостоящим процессом и при этом не обладает обобщенностью полученных результатов. В связи с этим возникает необходимость в развитии теоретических и численных методов оптимизации, основанных на математическом моделировании катодных процессов, в частности электрофизических. Теоретический подход к решению электрофизической задачи оптимизации изложен в работах [1-2]. В этих работах в различных постановках решается краевая электрофизическая задача, однако при этом не рассматривается прохождение тока во всем объеме катодного узла, т.е. исследование проводится без учета влияния массивной обоймы. В работе [3] при помощи метода конечных разностей решается задача в более строгой постановке, т.е. для системы «электродная вставка – обойма» в целом. Однако предложенный алгоритм имеет недостатки, связанные с реализацией для элементов сложной геометрической конфигурации. Кроме того, элементы катодного узла обладают различными электрофизическими свойствами, поэтому численное моделирование целесообразно проводить при помощи метода конечных элементов.

В последнее время для моделирования физических процессов используются разнообразные пакеты программ, основанные на различных численных методах. В частности, для расчетов методом конечных элементов широко используется программный пакет COMSOL Multiphysics [4]. Достоинством данного продукта является возможность моделирования как одного, так и нескольких связанных физических процессов, учитывая при этом изменение физических параметров в зависимости от времени, температуры и других факторов.

В данной работе проведено численное моделирование стационарной электрофизической задачи для катодного узла, представляющего из себя два соосно сопряженных элемента, при помощи пакета COMSOL Multiphysics.

Постановка задачи

Модель катодного узла представляет собой два соосно сопряженных элемента: вольфрамовый катодный стержень, запрессованный в медную цилиндрическую обойму (рис. 1). На торец стержневого катода в пределах контакта с плазмой дугового разряда радиусом r0 – в область катодного пятна – поступает электрический ток. Ввиду отсутствия экспериментальных данных по распределению плотности тока j0(r) в области пятна считаем эту величину по- стоянной.

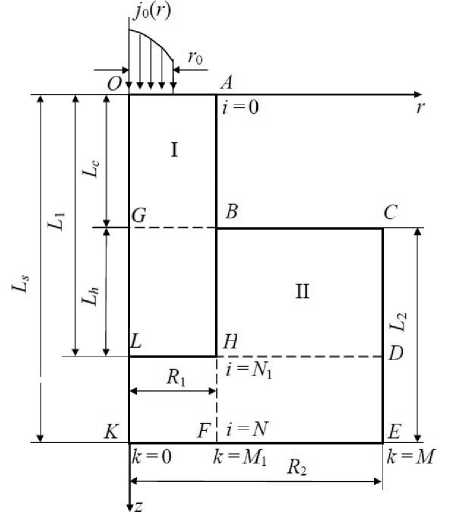
Рисунок 1 – Модель катодного узла:

I – катод (вставка), II – катододержатель (обойма)

Для рассматриваемой осесимметричной модели исследование стационарного распреде- ления электрического потенциала состоит в решении уравнения неразрывности тока:

1 а " r д U" + д " 1 д" = 0, r дr _ p(T) дr _ дz [ p(T) дz \ п.     1 д U   .     1 д U этом Jc = V Jr + Jz , Jr =---и Jz =. p дr         p оz

Граничные условия следующие:

• 1)    на рабочем торце катода (линия OA )

  1    д U ( r ,0)

  P 1 (T )    5 z

  
  

  —

  
  

^ для области катодного пятна (0 <  r <  f o ); π r 0²

• 1    д U ( r ,0)   _       ,                           , .

  .

  
  

Результаты и их обсуждение

На рисунке 2 показаны эквипотенциали и линии электрического тока в теле катодного узла «вставка - обойма». Длина вылета катодной вставки при этом L c = 0,5 см. Справа от рисунков помещена цветная шкала значения потенциала (в мВ). Размер стрелок на рисунках, указывающих направление тока, пропорционален значению плотности тока и нормирован на максимальное значение плотности тока на текущем графике.

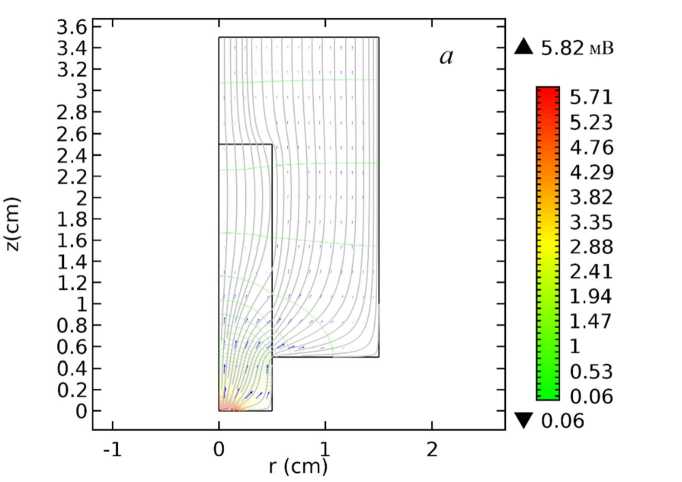
а

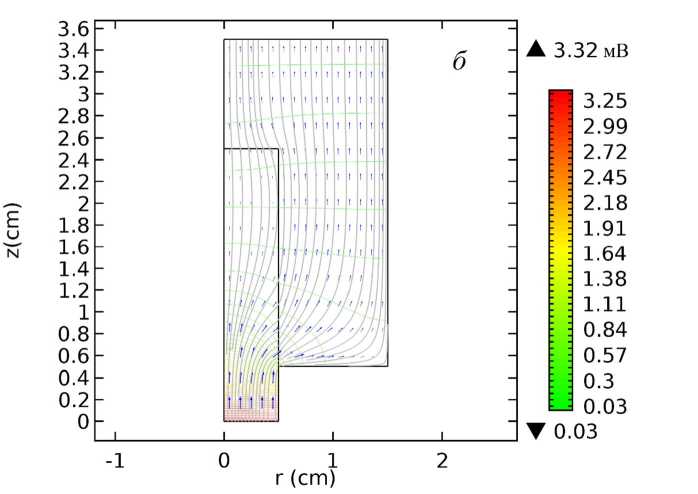
б

Рисунок 2 – Эквипотенциали и линии тока в катодном узле при L c = 0,5 см

На рисунке 2 а распределение электрических величин соответствует катодному пятну радиуса r0 = 0,2 см. Большие градиенты jc, реализующиеся в области пятна, отмечены густой сетью характерных линий. Ближе к переднему торцу обоймы плотность тока во вставке снижается и распределяется равномерно по объему. В той части вставки, которая находится в обойме (на глубине около 1,1 см от рабочего торца катода), происходит заметное уменьшение плотности тока. Это связано с уходом тока через боковую поверхность электрода, где ток имеет практически однородное распределение.

Эквипотенциали и линии тока на рисунке 2 б соответствуют катодному пятну радиуса r 0 = 0,5 см, таким образом, пятно в этом случае занимает всю площадь рабочего торца катода. Максимальное значение потенциала здесь снизилось до 3,32 мВ по сравнению с 5,82 мВ в предыдущем случае. Распределение плотностей тока во вставке становится однородным вплоть до переднего торца обоймы, где начинается уход тока. В области вставки, находящейся в обойме, как и в предыдущем случае, наблюдается снижение плотности тока. Однако существенное снижение плотности тока во вставке происходит несколько глубже (на глубине около 1,3 см от рабочего торца катода).

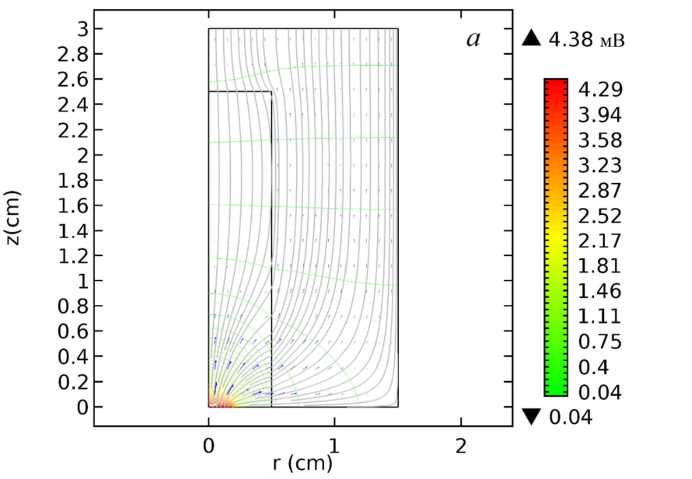
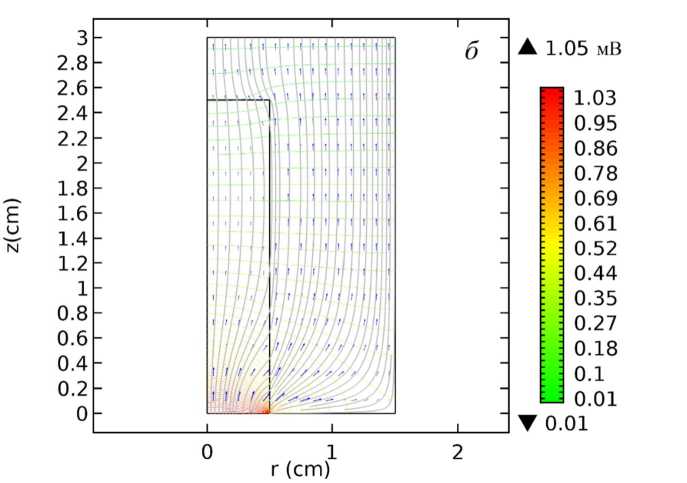
б

Рисунок 3 – Эквипотенциали и линии тока в катодном узле при L c = 0 см

На рисунке 3 показаны эквипотенциали и линии тока для катода при L c =0 см. На рисунке 3 а катодное пятно имеет радиус r 0 = 0,2 см, а на рисунке 3 б – r 0 = 0,5 см. Стоит отметить общее снижение максимального значения потенциала по сравнению с предыдущим случаем: с 5,82 до 4,38 мВ при r 0 = 0,2 см и с 3,32 до 1,05 мВ при r 0 = 0,5 см. Поскольку рабочий торец катода теперь заподлицо с передним торцом обоймы, линии тока сразу уходят из вставки в обойму. Однако в отличие от случая выступающего из обоймы стержня здесь наблюдается возврат тока обратно в катодную вставку. Возврат тока происходит на глубине около 1,8 см как в случае маленького, так и в случае большого катодного пятна.

Заключение

Проведено численное моделирование электрофизической задачи для катодного узла в строгой постановке «вставка – обойма». Получены стационарные распределения электрического потенциала и электрического тока в теле катодного узла. Показаны особенности протекания тока в зависимости от геометрии модели катода и радиуса катодного пятна дугового разряда.