Моделирование электромагнитных полей тяговых сетей с учетом металлических конструкций портального типа

В пространстве, окружающем объекты транспортной электроэнергетики, наблюдаются значительные уровни электромагнитных полей, которые могут оказывать негативное влияние на персонал, природную среду и электронное оборудование [1, 2]. Для снижения воздействия ЭМП применяются различные мероприятия, рациональный выбор которых в современных условиях [3] должен осуществляться на основе компьютерного моделирования. Для его проведения необходима разработка цифровых моделей, обеспечивающих адекватное определение ЭМП. Актуальность этой задачи подтверждается большим числом работ по данной тематике. Так, например, статья [4] посвящена расчету электромагнитных влияний ТС на смежные линии. В ней показано, что наведенные потенциалы, создаваемые ЭМП, могут представлять угрозу жизни и здоровью людей, а также генерировать помехи, вызывающие отказы низковольтного оборудования. В работе [5] даны аналитические соотношения, позволяющие определять напряженности ЭМП, создаваемые сложными ТС постоянного тока, и выполнено сравнение расчетных данных с экспериментальными. Результаты определения ЭМП вблизи контактной сети и контура заземления приведены в [6]. Статья [7] посвящена алгоритмам вычисления магнитных полей ТС и анализу влияния экранирования на распределение напряженности вдоль железнодорожного пути. Метод экспериментального определения ЭМП при коротких замыканиях (КЗ) контактных подвесок на рельсы представлен в статье [8]. В ней показано, что он позволяет оценить помехи и разработать защиту для слаботочного оборудования. Способ прогнозирования ЭМП в эксперименте по КЗ описан в [9]. Воздействие на персонал поля, создаваемого выпрямительными преобразователями тяговых подстанций (ТП), рассмотрено в [10]. Оценка низкочастотного ЭМП вблизи электроустановок дана в [11]. На этой основе предложен принцип нормирования ЭМП частотой 50 Гц. Результаты моделирования магнитного поля вокруг ТС, питающей высокоскоростные поезда, приведены в [12]. Оценка электромагнитного воздействия ТС на воздушные линии железнодорожной связи дана в [13], там же проведен анализ гармоник тягового тока и представлено теоретическое исследование их влияния на системы связи. Работа [14] посвящена вопросам использования программных модулей Comsol Multiphysics для нахождения напряженностей ЭМП вблизи высоковольтной линии электропередачи (ЛЭП). Результаты расчета ЭМП в пространстве между трассами ЛЭП и железной дорогой приведены в [15]. Модель для вычисления напряженностей ЭМП промышленной частоты, создаваемых воздушной ЛЭП, описана в [16].

Анализ рассмотренных публикаций позволяет сделать вывод о том, что в них представлены разработки, направленные в основном на определение плоско-параллельных ЭМП, создаваемых ТС и ЛЭП. Для этих полей выполняются следующие соотношения:

E ( x k , y k , z ) = const; H ( x k , y k , z ) = const;

x k = const; y k = const; z = var;                                                   (1)

где E , H – напряженности электрического и магнитного поля в фиксированных точках с координатами x k , y k по осям Х , Y (рис. 1); Z – ось, расположенная вдоль трассы дороги.

Одним из основных элементов любой ТС являются металлические или железобетонные опоры, вблизи которых характер распределения напряженностей ЭМП усложняется; при этом картина поля становится трехмерной и соотношения (1) не выполняются. Особенно заметные вариации ЭМП имеют место в режимах КЗ, когда в цепь замыкания включаются элементы опоры.

Для решения задачи определения ЭМП с учетом влияния опор или других металлических конструкций, находящихся на трассе ТС, например путепроводов, может использоваться подход, предложенный в работах [17–19].

Постановка задачи и результаты моделирования

Ниже приведены результаты разработки цифровых моделей для определения ЭМП вблизи жестких поперечин, представляющих собой металлические конструкции портального типа (рис. 1).

Рассматривалось два режима работы ТС двухпутного участка: нормальный при нагрузках по каждому пути 8 + j 8 МВ·А в конце ТС при консольном питании контактных подвесок; короткое замыкание через элементы жесткой поперечины (рис. 2а); сопротивление ее заземления принято равным 10 Ом.

Моделирование включало следующие этапы:

• •    формирование цифровой модели системы тягового электроснабжения (СТЭ), в состав которой наряду с протяженными элементами (контактная сеть и рельсы) включался набор проводников ограниченной длины, моделирующих жесткую поперечину и примыкающий к ней участок ТС;

• •    расчет режима СТЭ;

• •    вычисление вертикальных и горизонтальных составляющих напряженностей ЭМП и определение на их основе амплитуд E max и H max ;

• •    формирование зависимостей E max = E max ( x ); H max = H max ( x ); E max = E max ( z ); H max = H max ( z );

НТ 1

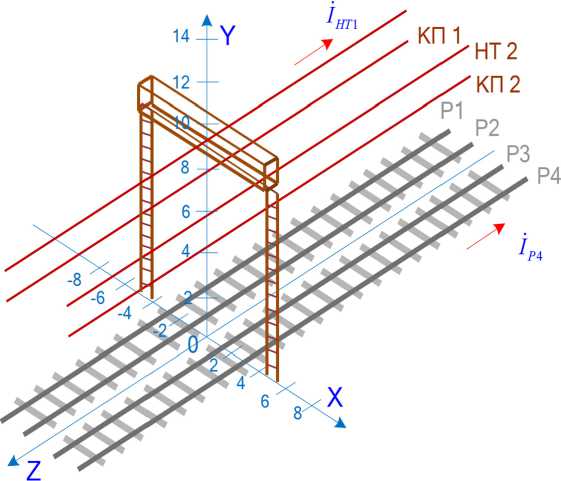
Рис. 1. Схема жесткой поперечины: НТ – несущие тросы; КП – контактные провда; Р – рельсовые нити

Fig. 1. Diagram of a rigid crossbar: HT – load–bearing cables; КП – contact wires; P – rail threads

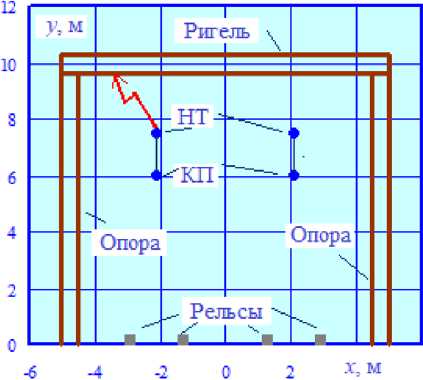
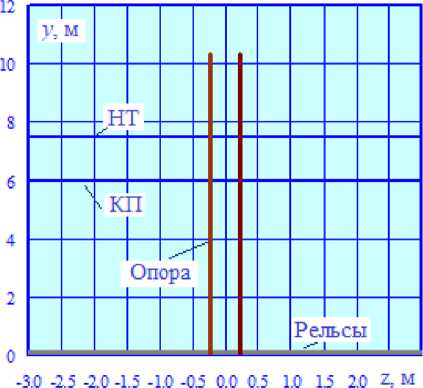
Рис. 2. Координаты токоведущих частей и элементов жесткой поперечины

Fig. 2. Coordinates of the live parts and elements of the rigid crossbar

б

• •    построение объемных диаграмм ЭМП.

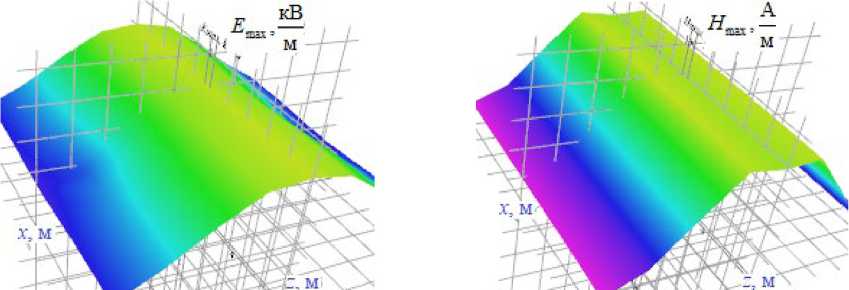
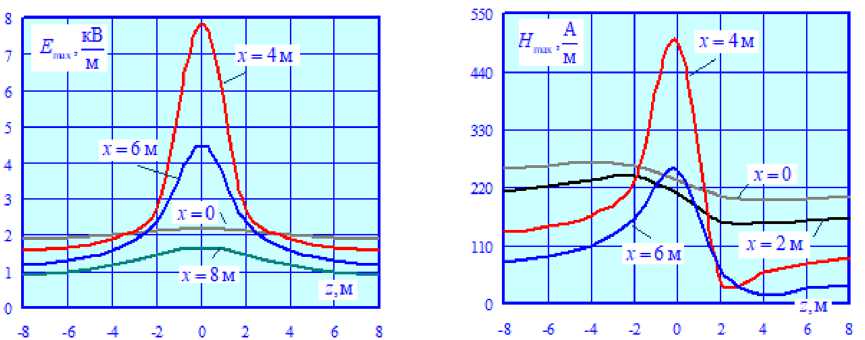
В результате моделирования были построены графики амплитуд напряженностей электрического E max и магнитного H max полей на высоте 1,8 м от координат х и z при нормальном режиме работы тяговой сети (рис. 3–6), а также при КЗ через элементы жесткой поперечины (рис. 8, 9). Пространственная структура распределения этих параметров при нормальном режиме работы ТС показана на рис. 7, при при КЗ – на рис. 10.

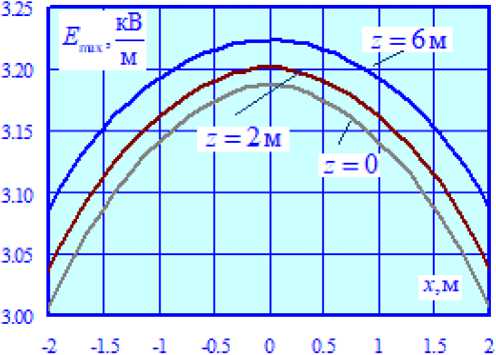
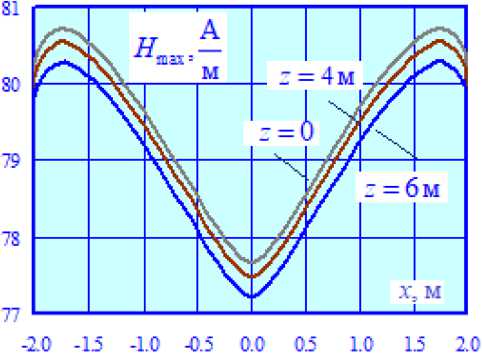
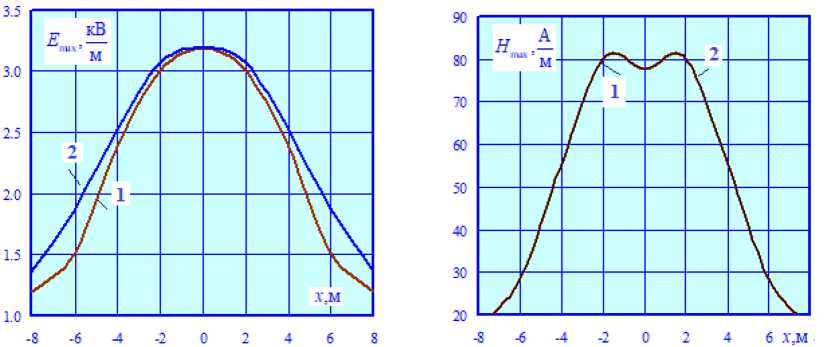
Из рис. 3а видно, что максимальное различие между кривыми E max = E max ( x ), построенными при z =0 и z =6 м, достигает 21 %, что подтверждает важность учета опор при определении ЭМП ТС. Отличия в графиках H max = H max ( x ) значительно меньше, при этом

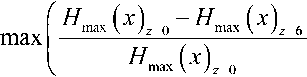
•100 =2,1% (рис. 3б). Зависимости E max

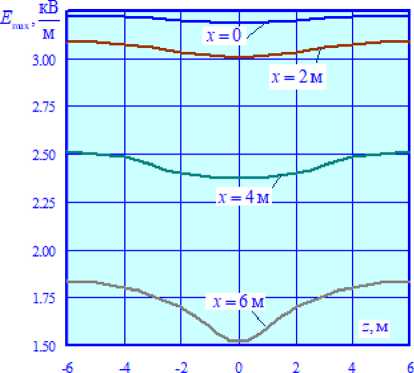
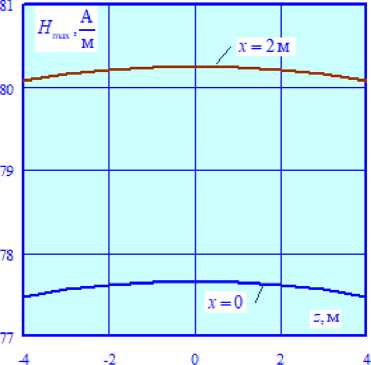
= E _max( z ) и H _max = H _max( z ), по-

лученные для разных значений координат х , показаны на рис. 4.

а

Рис. 3. Зависимости E _max = E _max( x ) (а) и H _max = H _max( x ) (б) при наличии жесткой поперечины

Fig. 3. Dependencies E max = E max ( x ) (а) and H max = H max ( x ) (б) in the presence of a rigid crossbar

б

Результаты сравнения напряженностей ЭМП, полученные при наличии и отсутствии жесткой поперечины, приведены на рис. 5, 6.

Из рис. 5, 6 видно, что при учете жесткой поперечины картина напряженностей электрического поля заметно изменяется, а характер зависимостей H _max = H _max( x ) и H _max = H _max( z ) остается прежним. Распределение ЭМП в пространстве при нормальном режиме работы ТС показано на рис. 7

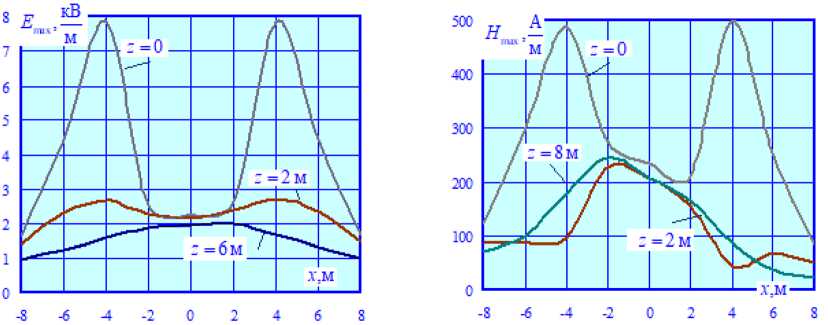
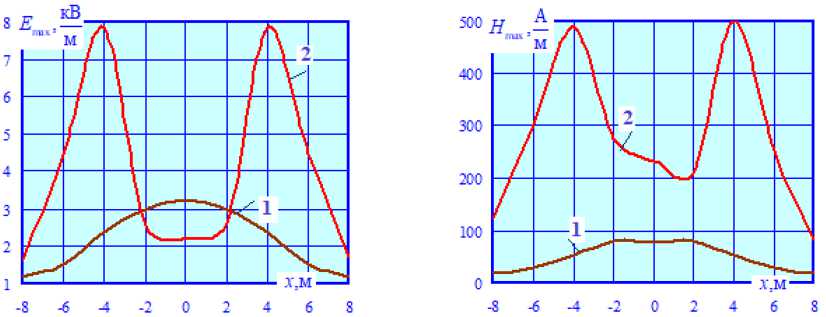
На рис. 8 и 9 представлены результаты расчетов КЗ при протекании токов замыкания через элементы опоры портального типа. Из них видно, что картина распределения ЭМП в пространстве в этом режиме заметно усложняется. Результаты сравнения E _max = E _max( x ) и H _max = H _max( x ), а также E _max = E _max( z ) и H _max = H _max( z ) представлены на рис. 11, 12.

Сводные данные, характеризующие результаты моделирования при коротком замыкании, приведены на рис. 13, 14.

а                                                б

Рис. 4. Зависимости E max = E max ( z ) (а) и H max = H max ( z ) (б) при наличии жесткой поперечины

Fig. 4. Dependencies E _max = E _max( z ) (а) and H _max = H _max( z ) (б) in the presence of a rigid crossbar

а                                                б

Рис. 5. Сравнение E _max = E _max( x ) (а) и H _max = H _max( x ) (б) при z = 0: 1 – при наличии жесткой поперечины; 2 – при ее отсутствии

Fig. 5. Comparison E _max = E _max( x ) (а) and H _max = H _max( x ) (б) at z = 0: 1 – in the presence of a rigid crossbar; 2 – in its absence

а                                               б

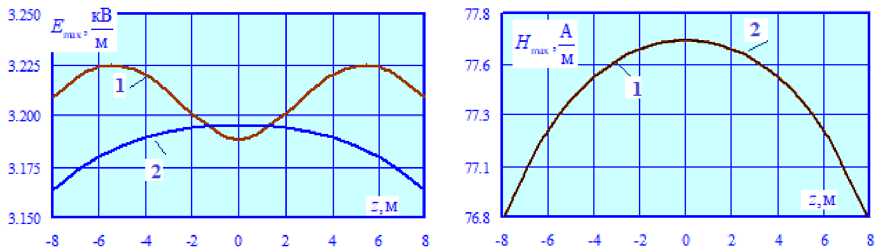
Рис. 6. Сравнение E _max = E _max( z ) (а) и H _max = H _max( z ) (б) при х = 0: 1 – при наличии жесткой поперечины; 2 – при ее отсутствии

Fig. 6. Comparison E _max = E _max( z ) (а) and H _max = H _max( z ) (б) at x = 0: 1 – in the presence of a rigid crossbar; 2 – in its absence

а

б

Рис. 7. Распределение ЭМП в пространстве при нормальном режиме работы ТС: а – электрическое поле; б – магнитное

• Fig. 7.    EMF distribution in space under normal vehicle operation mode: a – electric field; b – magneti

а

б

Рис. 8. Зависимости E max = E max ( x ) (а) и H max = H max ( x ) (б) при коротком замыкании

• Fig. 8.    Dependencies E max = E max ( x ) (а) and H max = H max ( x ) (б) in case of a short circuit

а

б

Рис. 9. Зависимости E max = E max ( z ) (а) и H max = H max ( z ) (б) при коротком замыкании

Fig. 9. Dependencies E max = E max ( z ) (а) and H max = H max ( z ) (б) in case of a short circuit

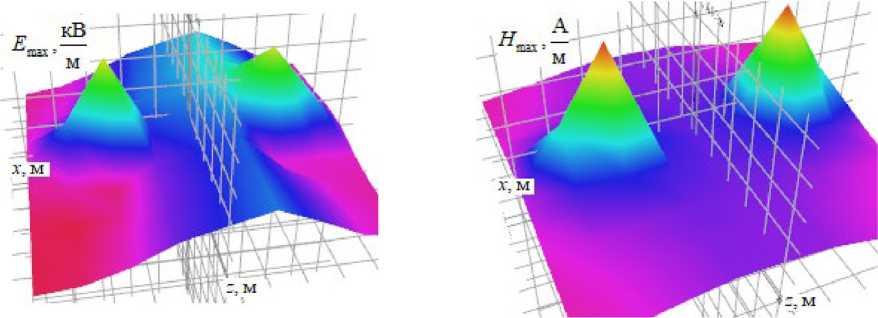
Рис. 10. Распределение ЭМП в пространстве при коротком замыкании вблизи конструкции портального типа: а – электрическое поле; б – магнитное

Fig. 10. EMF distribution in space during a short circuit near a portal-type structure: a – electric field; b – magnetic

а

б

Рис. 11. Сравнение E max = E max ( x ) (а) и H max = H max ( x ) (б) при z = 0: 1 – нормальный режим; 2 – КЗ

Fig. 11. Comparison E max = E max ( x ) (а) and H max = H max ( x ) (б) at z = 0: 1 – normal mode; 2 – short circuit

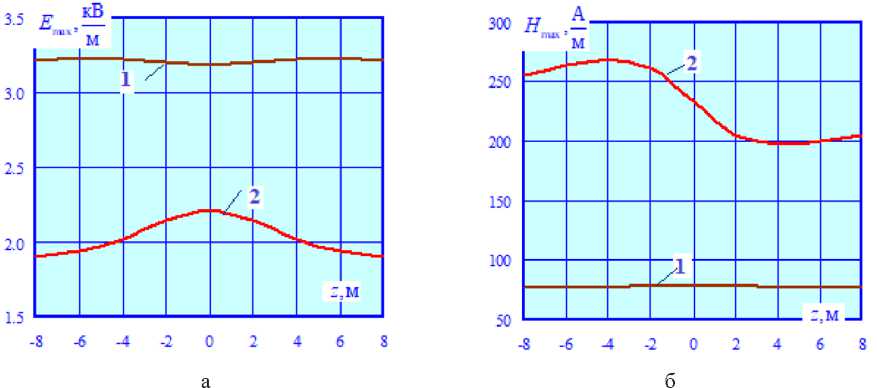
Рис. 12. Сравнение E max = E max ( z ) (а) и H max = H max ( z ) (б) при х = 0: 1 – нормальный режим; 2 – КЗ

Fig. 12. Comparison E max = E max ( z ) (а) and H max = H max ( z ) (б) at x = 0: 1 – normal mode; 2 – short circuit

:■:■:■:■:■:■:■:■:■:■:■:■:■:■:■:■:■:■:■:■:■:■:■
я	ъ	кВ
1		м

0.0

5.0

а

10.0

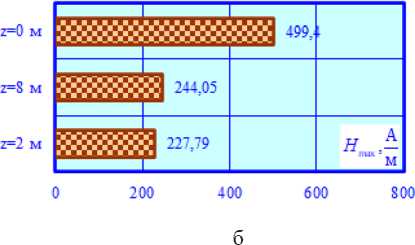
Рис. 13. Максимумы E max = E max ( x ) (а) и H max = H max ( x ) (б) при КЗ через элементы конструкции портального типа

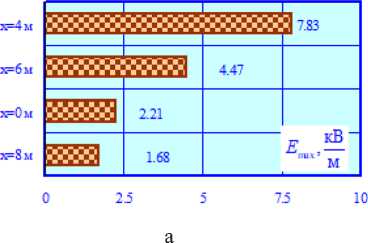
Рис. 14. Максимумы E _max = E _max( z ) (а) и H _max = H _max( z ) (б) при КЗ через элементы конструкции портального типа

Fig. 13. Maxima E max = E max ( x ) (а) and H max = H max ( x ) (б) in case of short circuit through portal-type structural elements

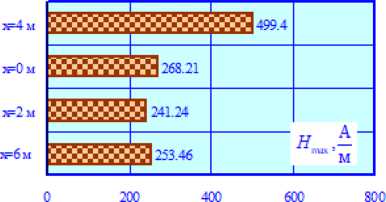
Fig. 14. Maxima E _max = E _max( z ) (а) and H _max = H _max( z ) (б) in case of short circuit through portal-type structural elements

Полученные результаты позволяют сделать следующие выводы:

• –    в нормальном режиме значения E max под жесткой поперечиной уменьшаются; на ее оси ( z = 0) максимальное снижение E _max достигает 24 %;

• –    при учете жесткой поперечины характер зависимости H max = H max ( x ) при z =0 не меняется;

• –    максимум амплитуды напряженности магнитного поля при замыкании контактной подвески на жесткую поперечину достигает 500 А/м; аналогичный параметр для электрического поля равен 7,8 кВ/м;

• –    наблюдается значительное увеличение E _max и H _max вблизи опор ( х = 4 м); так, например, E max достигает 7,8 кВ/м, а H max – 500 А/м;

• –    трехмерное электромагнитное поле при замыкании контактной подвески через элементы жесткой поперечины приобретает сложную структуру.

Заключение

Представлена методика и цифровые модели, позволяющие осуществлять корректный учет влияния жестких поперечин при моделировании электромагнитных полей тяговых сетей. Отличия предлагаемого подхода от известных состоят в следующем: расчеты ЭМП проводятся на основе результатов определения нормальных и аварийных режимов СТЭ; для учета жестких поперечин используется концепция проводников ограниченной длины, которые рассматриваются в виде единого объекта, формирующего ЭМП; в его состав входят следующие элементы: стержни опоры, ригель и набор коротких проводов, отвечающих контактной подвеске и рельсам.

Методика реализована в промышленном программном комплексе Fazonord, является универсальной и может применяться для определения ЭМП на любых объектах электроэнергетики и транспорта, вблизи которых находятся проводящие конструкции и сооружения.