Моделирование электронной структуры и расчёт основных электро-физических параметров аморфного кремния

Техническая реализация подобных технологий принципиальных затруднений обычно не вызывает, если, однако , известна ширина запрещённой зоны полупроводника, которую должны преодолеть возбуждённые валентные электроны, чтобы попасть в зону проводимости. Это в простейшем случае. В общем случае необходимо чётко знать структуру электронных состояний материала конкретного полупроводника, чтобы установить возможность достижения необходимой концентрации носителей и обоснованно определить способ и режимы управления этой концентрацией. При этом особую ценность обретает знание структуры электронных состояний химически чистого бездефектного, то есть собственного полупроводника, которое помимо получения надёжных результатов в изучении его свойств [1] позволяет доказательно выбрать легирующую примесь, её концентрацию и технологию легирования. Задача расчёта возможных электронных состояний для кристаллического материала, в том числе полупроводника, успешно решается методами зонной теории , основанной на понятии периодичности и трансляционной симметрии атомной структуры кристалла. Однако в аморфных веществах явная периодичность и трансляционная симметрия, по крайней мере, в их общепринятом, традиционном понимании, отсутствуют. Это существенно ограничивает применение к ним положений зонной теории и практически исключает теоретическое моделирование электронных состояний аморфных веществ современными методами и, как следствие, весьма затрудняет инженерный расчёт полупроводниковых приборов на их основе. Поскольку при этом аморфные полупроводники обладают целым рядом уникальных свойств [2-4], возникает острое противоречие между заманчивыми перспективами их применения в электронике и отсутствием эффективной методики теоретического моделирование электронных состояний аморфных материалов. Такое противоречие можно отнести к одной из основных проблем традиционной электроники и развивающейся наноэлектроники .

Для решения поставленной проблемы разработан авторский способ фрактального моделирования порождения аморфности тетраэдрической атомной структуры [5], и построена трёхмерная модель атомной структуры химически чистого аморфного кремния, которая исключает случайность в расположении его атомов и позволяет установить связь между структурой и физическими свойствами вещества. При этом необходимость решения уравнения Шрёдингера сохраняется, но возникает возможность расчёта электронного состояния вещества средствами квантовой (компьютерной) химии. Отсюда цель исследования -средствами компьютерной химии установить спектр электронных состояний для модельного кластера атомной структуры аморфного кремния (a-Si) и на основе полученных результатов вычислить основные электрофизические свойства кластера - ширину его запрещённой зоны, энергию уровня Ферми и концентрацию электронов в валентной зоне и зоне проводимости.

Для достижения поставленной цели построена трёхмерная фрактальная модель 16-и атомного кластера аморфного кремния. Расчёт основного энергетического состояния ( Ground State ) модельного кластера выполнен в среде GaussView/Gaussian , доступ к которой любезно предоставлен авторам сотрудниками Воронежского государственного университета, методом функционала плотности ( DFT) при общем нулевом заряде кластера с применением стандартного набора базисных функций 6-31 G . Численные результаты моделирования графически интерпретированы свободно распространяемой программой GaussSum и в виде иллюстраций представлены на рисунках 1-3. На диаграмме рисунка 1 в интервале энергий E от -20 эВ до 20 эВ штрихами показаны энергетические уровни модельного кластера, образующие его энергетические зоны: остовую, валентную, проводимости и запрещённую, а непрерывная замысловатая кривая - не что иное, как график плотности электронных состояний N ( E ) модельного кластера. Особый интерес вызывают окрестности запрещённой зоны E g , ограниченной потолком E_v валентной зоны и дном E c зоны проводимости, которые с целью детализации показаны на рисунке 2 в крупном масштабе и с меньшим шагом аппроксимации кривой N ( E) . Плотность электронных состояний N ( E ) внутри запрещённой зоны получена равной нулю , что соответствует теории [1-4] и видно на графике рисунка 2. При этом в масштабе и с шагом аппроксимации близким к условиям натурного эксперимента модельная кривая N ( E ) в окрестностях запрещённой зоны (рисунок 3, а ) хорошо согласуется с кривой плотности электронных состояний Коэна-Фрицше-Овшинского (КФО) [3], показанной на рисунке 3, б .

Далее приведен расчёт основных параметров a-Si. Результаты численного моделирования показывают, что в основном состоянии энергия потолка валентной зоны Ev модельного кластера составляет -3,555 эВ, а энергия дна его зоны проводимости Ec равна -2,375 эВ (рисунок 2). Отсюда определяются важнейшие параметры всякого собственного полупроводника: ширина запрещённой зоны Eg и уровень энергии Ферми EF. В нашем случае Eg=Ec-Ev =1,180 эВ, что с точностью до 0,04 эВ согласуются с экспериментальными данными [6], и поскольку уровень Ферми в основном состоя- нии собственного полупроводника расположен точно посередине его запрещённой зоны, то для модельного кластера EF =-2,965 эВ.

При этом величина E c показывает ещё и минимальную энергию ионизации E « > E_c =-2,375 эВ, необходимую для возбуждения атомов a-Si, например световым облучением, с целью генерации электронно-дырочных пар и переброски валентных электронов в зону проводимости.

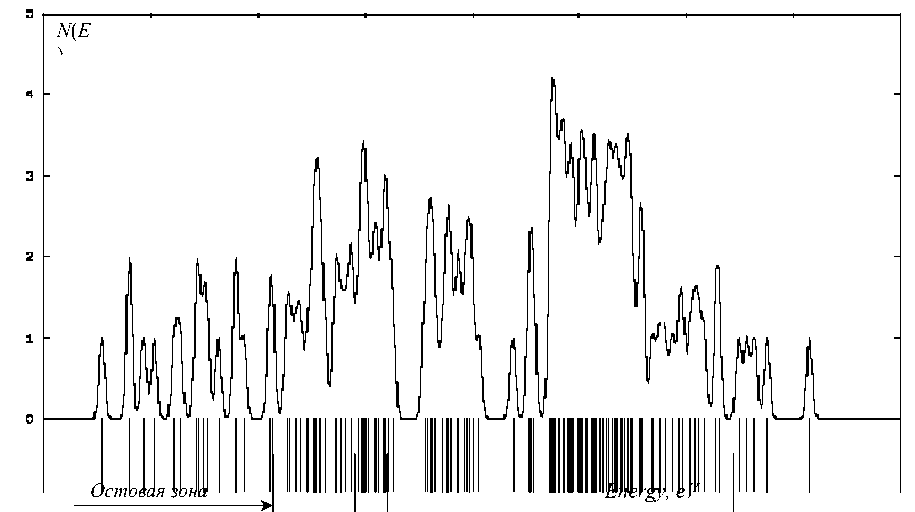
Валентная зона

Зона проводимости

Запрещённая зона

Рисунок 1. Диаграмма электронных состояний атомного кластера аморфного кремния

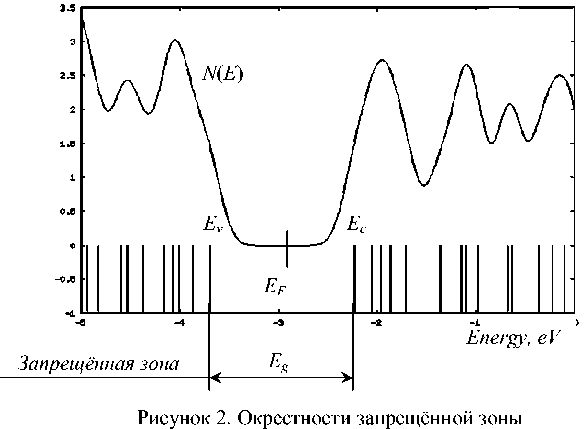
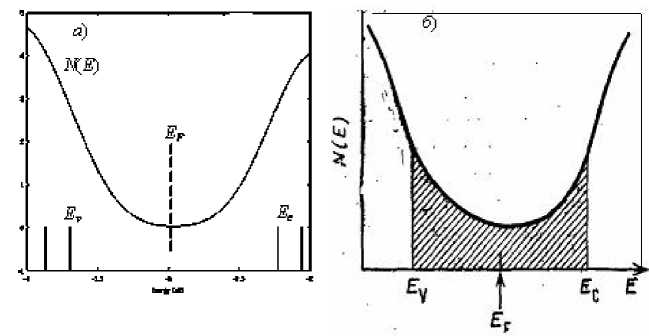
Рисунок 3. График N ( E ) плотности электронных состояний аморфного кремния в окрестностях его запрещённой зоны: а – авторская кривая; б – кривая КФО

Теперь о главном. Согласно теории [6], концентрация n электронов полупроводника во всяком интервале энергии E ₁ < E < E 2 определяется соотношением:

n = f f ( E,T ) • N ( E ) • dE ,      (1)

E 1

где f ( E,T ) – функция Ферми, показывающая вероятность обнаружения при температуре T электрона в состоянии с энергией E .

Функция Ферми вычисляется достаточно просто [6]:

f ( E,T ) =

exp I

E - E f kT

+ 1

где k – постоянная Больцмана.

Результаты проведённого моделирования дали весь спектр численных значений возможных энергий E электрона и плотности N ( E ) электронных состояний модельного кластера . Значение энергии Ферми E F вычислено и равно -2,965 эВ. Поэтому ничто не мешает рас-

считать искомую концентрацию n электронов аморфного кремния в любом интервале энергии -20 эВ < E < 20 эВ.

Такой расчёт выполнен для четырёх наиболее интересных на наш взгляд интервалов энергии электрона:

• а )    от -6.282 эВ до -6.272 эВ;

• б )    от -3.72 эВ до -3.67 эВ;

• в )    от -2.255 эВ до -2.205 эВ;

• г )    от 3.764 эВ до 3.819 эВ.

Поскольку при этом кривая N ( E ) точечно‐заданная и шаг её аппроксимации достаточно мал, то вычисление концентрации электронов в предусмотренных интервалах энергий проведено не интегрированием (1), а суммированием:

n = 2 f_t ( E,T ) • N ( E ) • dE       (3)

при T =300 ° К, А 1,38062 ^ 10^2:Дж ° К и соотношении 1 эВ = 1,60219Д0 " ¹⁹Дж [8]. Результаты вычислений концентрации электронов для интервала энергий от -6.282 до -6.272 эВ даны в таблице 1.

Интервал дискретных значений энергий [-6.282 эВ, -6.272 эВ] расположен в той части валентной зоны модельного кластера (рисунок 1), где все энергетические уровни в основном состоянии гарантированно заняты электронами. Именно поэтому вероятность f ( E,T ) обнаружить при T =300 ° К электрон с любой энергией в интервале от -6.282 эВ до 6.272 эВ равна 1. Это ничуть не противоречит квантовой механике, которая априори допускает, что электрон одновременно находится на всех уровнях рассматриваемого интервала энергий.

Таблица 1

Результаты вычислений концентрацию электронов аморфного кремния в интервале энергии от -6.282 до -6.272 эВ

№	E	N ( E )	f ( E,T )	f ( E,T) ■ N ( E )	n
1	-6.282	1.99863416077	1	1.99863416077	0.0219
2	-6.281	1.99659625892	1	1.99659625892
3	-6.28	1.99452243027	1	1.99452243027
4	-6.279	1.99241347505	1	1.99241347505
5	-6.278	1.99027019481	1	1.99027019481
6	-6.277	1.98809339224	1	1.98809339224
7	-6.276	1.9858838709	1	1.9858838709
8	-6.275	1.98364243499	1	1.98364243499
9	-6.274	1.9813698891	1	1.9813698891
10	-6.273	1.97906703799	1	1.97906703799
11	-6.272	1.97673468636	1	1.97673468636

Концентрация n электронов аморфного кремния в интервале -6.282 эВ < E < -6.272 эВ при шаге аппроксимации dE= 0.001 эВ составила 0.0219 электрона на каждый уровень этого интервала. Результаты выполненного моделирования дают ширину заполненной части валентной зоны аморфного кремния равной 1,437 эВ, и несложный расчёт с относительной ошибкой менее 2% определяет общее количество валентных электронов модельного кластера с учётом их спина в 62,9406 единиц против 64-х фактических.

Интервал энергий [-3.72 эВ, -3.67 эВ], показанный в таблице 2, как и предыдущий интервал, расположен в валентной зоне модельного кластера (рисунок 1). Поэтому веро- стигает 1 (столбец 6 таблицы 2), но концентрация электронов в этом интервале всего 0.0428 электрона на 0,005 эВ (столбец 8 таблицы 2). Их там практически нет и уровни этого интервала свободны. Здесь следует вспомнить, что расчёт электронных состояний модельного кластера выполнен для его основного состояния, в котором у потолка валентной зоны существуют [6] свободные энергетические уровни, на которые могут переходить валентные электроны, не отрываясь от остова. Именно эти уровни обнаружены при моделировании. Столбцы 5, 6 и 7 таблицы 2 в качестве иллюстраций содержат численные значения величин N(Em), fEm,T) иfEm,T)• N(Em) для энергии Em из середины соответствующего интервала.

ятность заполнения его электронами тоже до-

Таблица 2

Результаты вычислений концентрацию электронов аморфного кремния по прочим интервалам энергии

№	E 1	E 2	dE	N ( E m )	fE m ,T)	fE m T • N ( E m )	n
1	2	3	4	5	6	7	8
1	-3.72	-3.67	0.005	0.998009973542	1.0000	0.998009973542	0.0428
2	-2.255	-2.205	0.005	0.999216024616	4.4867e-013	4.4832e-013	2.2559e-014
3	3.764	3.819	0.055	4.20393949684	3.0911e-114	1.2995e-113	9.7229e-114

Интервал энергий от -2.255 до -2.205 эВ (таблица 2) содержится в придонной части зоны проводимости модельного кластера (рисунок 1) и вероятность его заполнения валентными электронами f ( E_m,T) =4.4867e-013 исчезающее мала. Ещё меньше теоретическая концентрация электронов в нём - 2.2559e-014 электрона на 0,005 эВ. Интервал пуст и это соответствует основному состоянию кластера. При возбуждении валентных электронов до энергий -2.255 эВ < E < -2.205 эВ они неизбежно появятся в этом интервале, где могут достигнуть концентрации не более 0.0428 единиц на каждые 0,005 эВ, так как концентрация электронов в любом интервале энергий всегда ограничена теоретической плотностью их состояний N ( E ). Таким образом, концентрация электронов в придонной части зоны проводимости модельного кластера теоретически не может превысить аналогичного показателя потолочных уровней валентной зоны (таблица 2) поскольку плотность электронных состояний в этих интервалах энергий практически одинакова. В связи с этим на графике рисунка 1 привлекает внимание заметный всплеск теоретической кривой N ( E ) в интервале энергий зоны проводимости от 3.764 эВ до 3.819 эВ, где следует ожидать наиболее высокой концентрации электронов, а значит наиболее высокой проводимости полупроводника. Действительно, в основном состоянии кластера вероятность появления электронов в этом интервале равна 3.0911 e-114, поэтому концентрация электронов в нём составляет 9.7229e-114 единиц на каждые 0.055

• эВ.    Однако при возбуждении валентных электронов энергией в 3.764 эВ и более функция Ферми f ( E,T =300 ° К) примет значение 1, и концентрация электронов достигнет 2.5349 единиц на 0.055 эВ. Это максимум, что можно взять от химически чистого аморфного кремния.

Таким образом, практические результаты выполненного исследования показывают, что применение авторской методики фрактального моделирования аморфных структур в сочетании с расчётными методами квантовой химии позволяет решить ряд фундаментальных научных и прикладных проблем, в том числе:

• 1.    Получить строго систематическое описание атомной структуры аморфного вещества, пригодное для теоретических исследований его электронных состояний.

• 2.    Рассчитать весь спектр электронных состояний аморфного вещества и на основе полученных результатов вычислить его главные электрофизические свойства: а ) ширину запрещённой зоны; б ) энергию Ферми; в ) энергию необходимой ионизации; г ) концентрацию электронов в валентной зоне и зоне проводимости.

• 3.    Решить ключевой вопрос развития электроники, обеспечив целенаправленное управление типом и концентрацией носителей заряда полупроводника.

• 4.    Установить связь между атомным строением и другими физическими свойствами аморфного вещества, в частности, его теплоёмкостью, магнитной восприимчивостью и другими термодинамическими величинами.