Моделирование электротепловых процессов в вентильном преобразователе системы самовозбуждения синхронного генератора при коротких замыканиях в энергосистеме

При коротких замыканиях (КЗ) в энергосистеме напряжение на выводах синхронного генератора (СГ) снижается. Для его восстановления выполняют двукратную форсировку путем увеличения тока ротора до двойного номинального значения. Для синхронных генераторов с тиристорными системами самовозбуждения (ССВ) это приводит к дополнительному нагреву вентилей тиристорного преобразователя (ТП) ССВ в сравнении с предшествующим режимом и увеличению температур полупроводниковых структур (ТПС) до нормируемой величины.

В системах самовозбуждения тиристорный преобразователь получает питание с выводов синхронного генератора, поэтому при близких КЗ, вследствие снижения напряжения на выводах, не всегда можно добиться увеличения тока возбужде- ния до двойного номинального значения. В таких режимах нагрузка вентильного преобразователя не достигает предельной, что приводит к меньшей интенсивности нагрева тиристоров. Кроме того, при КЗ с длительностью, не превышающей предельно допустимую длительность форсировки генератора, ТПС вентилей также не успевают достичь нормируемого значения. В работе [1] показано, что в этих случаях, тем не менее, возможна форсировка и при отказах параллельных вентильных ветвей в сильноточных ТП. Однако для исследования таких режимов работы сильноточного ТП и разработки соответствующих алгоритмов управления им необходима математическая модель, связывающая электромагнитные переходные процессы в СГ с элек-тротепловыми процессами в ТП ССВ.

Рассмотрим некоторые особенности расчета электротепловых процессов в сильноточном тиристорном преобразователе ССВ на примере математической модели синхронного генератора с самовозбуждением, описывающей электромагнитные переходные процессы в его обмотках при внешнем КЗ произвольного вида n [2].

Исходная модель генератора основана на совместном решении общеизвестной системы дифференциальных уравнений Парка-Горьева с уравнением внешней характеристики ТП ССВ. Такая система дифференциальных уравнений, записанная в операторной форме в d , q -осях ротора без учета процессов в поперечной оси, имеет вид [3]:

Решением преобразованной системы уравнений относительно выпрямленной составляющей тока в цепи ротора будет следующая зависимость [2, 3]:

/ (Л-T' p ^pd r^{m 1} .l' ^pP2 2 ■“ t              ZIA

I d *⁽ t ^{) -} I d 0 * ^{e        +} I d 0 * ^e        ,                  ⁽²⁾

^где I d 0 *

X

’ Id 0 * ^{+ (} I d 0 * ^xad * ^xd * ^xd *      .

;

• вн * ) ) ^Х

^Xad *

d 0 * ^xad *

x d * ⁺ x вн * ) ) ^х

+ Y⁽ nn x d * ¹ T a *

xad * P v xad * P

xad. * r f * + X f * p x ad * P

I xad *		I i d *A		I 0 I
xad * P	x	I d *	-	U d *	, (1)
r kd * + xkd * P )		V I kd * )		V 0 у

X

( n )

-d * ^{T x} вн *

P d 1 ^-

( ^xkd *   ^xad * ^{) x}ad *

_

^xd * ^xd *

xf * xkd * xad *    xad*( xa rd *)( xd *+ x вн * ) + re * xad *

'вн*/ )

;

;

^xf *

где i d * - ток статора в d-оси; I d * , U_d * - выпрямленные составляющие тока и напряжения ротора; I kd * — ток в цепи эквивалентной продольной демпферной обмотки ротора; x вн * - эквивалентное внешнее сопротивление, отделяющее точку КЗ от выводов СГ. Остальные сопротивления заимствованы из общеизвестных схем замещения СГ, при этом все параметры выражены в долях базисных величин статора и ротора.

Заменим в выражении (1) постоянную составляющую напряжения на роторе уравнением внешней характеристики ТП ССВ из работы [2], полученным для произвольного вида КЗ с учетом различных способов управления тиристорами и режимов их работы:

J Е 2 * + Е 2 *     (           Ед * I

Ud* -  --------— cosI «ср + arctg ,A I “ л        V          EB*)

₌ _ Z kd * ^Pd 2

^xkd *

.

В выражении (2) сопротивления r e * и r d * в процессе форсировки могут меняться, так как первое из них зависит от режима работы ТП и углов управления вентилями, а второе – от величины тока ротора. Поэтому коэффициент затухания p d 1 является зависимым от времени. Для учета этой зависимости разобьем ось времени на малые интервалы с шагом Δ T . Тогда выражение (2) можно записать в дискретной форме для произвольного интервала T i , полагая при этом, что в его пределах величина p d 1 неизменна и равна p d 1 ( T i –1 ):

' I d * ( T i)- I d * ( T i - 1 ) e ^P d ^{1 ( T -1>} “ ^{a t} ;

< I d * ( T ) - I d * ( T i - 1 ) e ^P d ²^^{a t} ;

_ I d * ( T ) - I d * ( T ) + I" d * ( T i ) .

где r_e

л

I 2л  Уср xу* + r у* I -      .

I d *    r e * i d * r d * I d * ,

I - 4 x вн * k ^{( n} ) x ₂ * sin ² « m x

_x k e    u б .

^K тсв ^Uf б ;

Для определения полного тока ротора учтем величины периодических составляющих, наводимых в его цепи. При симметричных КЗ генератора это периодическая составляющая основной частоты, при несимметричных КЗ – основной и двойной частот [4]:

3 ж I О rd * =- Xy* + I 2 л V

3y i y ср

2 л ) r ^y* ;

I d * ( T i ) - ( I d *⁽ 0 ⁾ + I d *⁽ 0 ) - I d 0 * ) x

ke - л

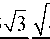
F4 ⁺ KFR I              K Г J I

-------B cos cz _n + arctg — EA .

I ^ср

³          V           KEB )

Ti x cos (mTi) e Ta при симметричных КЗ;

i f * ( T ) - ^ I d * ( T i ) - 2 ( I d *⁽ 0 ) + I d *⁽ 0 ) - I d 0 * ) sin у рот X

В данном выражении K тсв и α m соответственно коэффициент и угол трансформации преобразовательного трансформатора ССВ, питающего тиристорный преобразователь, а составляющие K_EA и K EB – коэффициенты, зависящие от удаленности КЗ, несимметрии питающих напряжений ТП и углов управления тиристорами.

Ti xsin(mTi) e Ta -(I'd*(0) + Id*(0)-Id0*)x

x cos ( 2 m T i ) при несимметричных КЗ,

где Т а – постоянная времени затухания апериодических токов фаз синхронного генератора; γ рот – угол поворота ротора относительно оси симметрии об-

мотки фазы «А» в момент короткого замыкания t КЗ . Величина t КЗ измеряется от точки перехода через нуль напряжения фазы «А» в начале периода.

Для расчета тепловых потерь, а затем и ТПС вентилей преобразователя ССВ необходимо знать токи тиристоров в открытом состоянии и напряжения, прикладываемые к ним при коммутациях. Полагая, что углы управления вентилями известны, причем в начале форсировки α_Т = 0, и для вентилей j -го плеча суммарный угол задержки определяется как « T j = « T j +v _T j , где V _T j — угол вынужденного запаздывания включения вентилей, обусловленный несимметрией питающих напряжений ТП и его режимом работы, запишем выражение для расчета токов плеч преобразователя в конце i -го интервала дискретизации:

i Tj * ⁽ T ⁾ = ‘

(±cos («Tj (T ))- cos (флjd_2 + иб UЛ j, j-2* ( Ti)

^+ю КЗ ^{+ m} T ^{)) x} ---- U fs     ² x y*

на интервале включения у _вкл ;

± i f J ( T ) на интервале открытого состояния P _T ;

' ± i f * ⁽ T ^)- ( ± cos ( « T j + 2 ⁽ T i ⁾ ) ^-

• - cos ( Ф л j + 2,j ⁺ ® t КЗ ⁺m Ti )) - u ⁶- x ^U f б

U -v+ j T i )

x----------на интервале

• ² x y^

выключения У выкл. ;

0 в остальных случаях.

Здесь величины U л _j , _{j - 2} * , U л _{j + 2}, _j , и углы Ф _л j j _{- 2} , Ф л j _{+ 2} j соответственно амплитуды и фазы линейных напряжений, питающих ТП, определяемые из решения системы уравнений (1) относительно токов в статоре генератора с учетом схемы и группы соединения обмоток преобразовательного трансформатора [2]. Токи вентилей катодной группы ТП взяты отрицательными и для их расчета данное выражение следует использовать с отрицательными знаками. Границы и длительности интервалов коммутации и проводящего интервала на i -м шаге дискретизации могут быть определены в соответствии с параметрами преобразователя, найденными на предыдущих итерациях, при этом на первой итерации значения этих углов следует брать из предшествующего замыканию установившегося режима.

Перейдем к определению мощностей тепловых потерь в вентилях и расчету температур их нагрева. Полная мощность тепловых потерь за период в вентиле преобразователя ССВ складывается из средних мощностей потерь в открытом состоянии, потерь от обратного тока, потерь при включении и запирании, потерь в закрытом со- стоянии, а также потерь на управляющем электроде. В сильноточных ТП наиболее существенными являются потери в открытом состоянии и при включении и выключении вентилей. Доля остальных, как правило, не превышает 2–5 %, в связи с чем ими обычно пренебрегают [5]. Из оставшихся наименее значимы потери при включении вентиля, поэтому ограничимся рассмотрением мощностей тепловых потерь только в открытом состоянии PT и при запирании тиристоров PRQ.

В процессе форсировки нагрев тиристоров носит периодический характер. Колебания мгновенных значений ТПС вентилей обусловлены как циклическим режимом работы самих тиристоров, так и искажением кривой полного тока ротора наводимыми в нем при КЗ периодическими составляющими. Учет данных факторов при расчете температур нагрева вентилей по усредненным за период значениям, согласно общепринятой методике, изложенной в работе [5] и применяемой при проектировании, значительно ее усложняет и делает практически не реализуемой в случае анализа несимметричных или длительных КЗ. В связи с этим рассмотрим расчет ТПС вентилей по мгновенным значениям, основываясь на предварительном разложении динамического теплового сопротивления тиристорного модуля на сумму сопротивлений отдельных его участков [6].

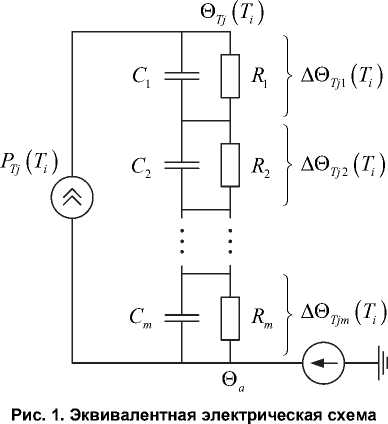
замещения тиристорного модуля j -го плеча

В соответствии со схемой, изображенной на рис. 1, представим кривую зависимости от времени динамического теплового сопротивления «переход–среда» тиристорного модуля в виде суммы экспонент:

( th ) tja

m

(t ) = z Rk к=1

t

—

1 - e ^R k C k

где m – количество рассматриваемых участков в модуле; Rk, Ck – соответственно собственное теп- ловое сопротивление и внешняя тепловая проводимость k-го участка.

Тогда мгновенное значение ТПС вентиля j -го плеча в ходе форсировки на любой из итераций расчета может быть найдено как

® Tj ( T M a ■ A)^ T i ) -0 a +

- -T- e RkCk , (4)

m

+ 2 P T ( T i ) R k - ( P T ( T i ) R k - j ( T i - 1 ) ) k - 1

, m tt,( Ti-1) + j Ti).

I T ( AV ) j ⁽ T i ⁾ -            2          ;

1 ^A t

” I RMS j ^{( T ) -} A T 00 i Tj ⁽ t ⁾ dt ^-

_ i j T - 1 ) + j TT i - 1 ) j T ) + j TTi)

_                                            3

■                      Tj ^{( T )} T ⁽ T i - 1 ⁾

где ZTj ( t ) = iTj (T-1)+ t--------AT-------- где Θа – температура охлаждающей среды; PTj (Ti) – средняя мощность тепловых потерь в вентиле на текущей итерации; ΔΘTjk (Ti–1) – приращение температуры k-го участка над температурой охлаждающей среды, найденное на предыдущей итерации.

Отметим, что при реализации расчета ТПС вентилей по формуле (4) точность и адекватность модели будет зависеть от шага дискретизации и, следовательно, во всех случаях шаг разбиения должен быть значительно меньше периода. Кроме того, для определения ТПС вентилей в первый момент КЗ необходим предварительный расчет мгновенных температур в предшествующем установившемся режиме работы генератора. В связи с этим первоначально рассмотрим расчет средней мощности тепловых потерь на интервале дискретизации, а затем получим формулы для расчета ТПС вентилей в предшествующем установившемся режиме. Так как в сильноточных преобразователях ССВ применяется параллельное соединение вентильных ветвей, то расчет будем проводить только для наиболее нагруженных вентилей в плечах.

Усредненные на интервале дискретизации тепловые потери в открытом состоянии в наиболее нагруженном вентиле j -го плеча определяются как

K K ²

P T ( AV ) j ⁽ T ) ^- U T ( TO ) I T ( AV ) j ⁽ Ti ⁾ ”N ⁺ r T I RMSj ⁽ Ti ⁾ ^ 2 , ⁽⁵⁾

Подставим выражения для токов в формулу (5) и запишем ее в окончательной форме:

P T ( AV ) j ^{( T ) -} U T ( TO )

i T ( T - 1 ) + ⁱTj ( Ti) к H

2 N

+ r_T

i Tj ( T i - 1 ) + i Tj ( T - 1 ) j T i ) + i Tj ( T ) к H

3                   N ^{2 .}

Для учета тепловых потерь на интервале за-

пирания первоначально найдем среднюю величину

обратного напряжения на плече как

U RQj ⁽ Ti) ^-

^- U л j , j + 2 ( T ) sin ( ^a T j + 2 ( T i ) ⁺ Y T j , j + 2 ( T i)) , тогда

^PRQ ( AV ) j ⁽ T i ^{) -}

U RQj ⁽ T i) ² t RQj ^{( T )}

URQj ^{( T )} K H

2 Ц  N

^QRR к

" di T к I ^- k

_ dt _

где t RQj – время запирания вентиля; i T к , Q RR к – значения классификационного тока тиристора и соответствующего ему заряда восстановления; k – коэффициент аппроксимации кривой заряда.

Время запирания тиристора может быть найдено следующим образом:

t RQj ⁽ T i)^- t RR к

x

di T к 1 k Г U RQj ^{( T )} K H

_ dt _

URQj ⁽ Ti) K H

2 L _Y    N

2 L _Y

-, 2 k -1

—J

N j.   и -2 k diTк

_ dt _

k

2 Q

--RR^X x t_{RR к}

,

где I_T ( _AV ) j , I_RMS j – соответственно среднее и действующее значения тока j -го плеча; N – число параллельных ветвей в плече; K Н – коэффициент неравномерности деления тока плеча по ветвям; U T ( TO ) , r T – соответственно пороговое напряжение и динамическое сопротивление вентиля в открытом состоянии.

Среднее значение тока j-го плеча на интервале усреднения потерь найдем, апп роксимируя кривую тока линейной зависимостью по значениям, найденным согласно выражению (3) в начале и конце i-го интервала (рис. 2). Тогда для расчета квадрата действующего значения достаточно проинтегрировать аппроксимированную зависимость на этом интервале, возведя ее в квадрат. Искомые выражения в именованных единицах имеют вид:

где t_{RR к} – время обратного восстановления тиристора, соответствующее классификационному току; k – коэффициент аппроксимации, единый для кривых заряда и времени обратного восстановления.

На практике длительность интервала t RQj в большинстве случаев оказывается значительно меньше длительности периода T и выбранного шага дискретизации расчета Δ Т , что обычно приводит к дополнительному уменьшению этого шага и увеличению числа итераций. Избежать этого можно путем замены интервала t_R Qj на интервал Δ Т с последующим эквивалентированием средней мощности тепловых потерь, как показано на рис. 3:

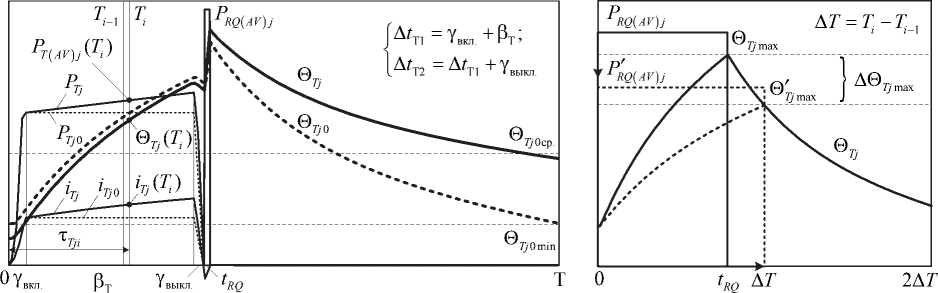
Рис. 2. Условные кривые мгновенных значений тока, мощности тепловых потерь и ТПС вентилей j -го плеча

Рис. 3. К расчету ТПС при запирании вентиля

P RQ ( av ) j ⁽ T ⁾ = P RQ ( av ) j ⁽ T ⁾

m f ( t RQj ⁽ T i ⁾ Z R e R k C k k = 1

1 _^L1

- 1 e ^R k C k

m

Z

R k

k = 1 V

'      а г Ц

1 - e R k C k

ных значений ТПС вентиля в установившемся режиме показана пунктиром. Запишем искомые выражения:

• интервал включения у _вкл :

t

m

^A® Tj 0вкл ⁽ t ⁾ = Z P Tj 0 ^Rk ^{1 +}

k = 1

R k C t

^^^™ „

e

i k C k - 1

+

V

Погрешность в определении максимального значения температуры, достигаемого в течение периода, может быть найдена как разность значений:

^A® Tj max ^{( T} i ⁾ = ® Tj max ⁽ Ti^^- ® Tj ' max ⁽ T ⁾ =

^+A® Tj 0min k ^e

t \ R k C k

/

• интервал открытого состояния P T :

f

m

= Z PRQ(AV) j (T) Rk k=1

V

1 - e

t RQj ^{( T} i ⁾

—-—-— R k C k

xRk

t JQT^

1 - e R k C k

-

f

A® ■ ( T i - 1 ) 1

⁺ V P RQ ( AV ) j ⁽ T ) ^X

^{A T -} Q T ⁾ Ц _AL

^R k C k      e R k C k

m

^A® Tj0oTKp ⁽ t ⁾ = Z P Tj0^Rk ⁺ P Tj 0 ^Rk

k = 1

V

^{+ A}® T 0min k

V

- -L_ )

) e -C.

)

Обобщая приведенные выше формулы, запи-

шем окончательное выражение для расчета мгно-

венных значений мощности тепловых потерь в наиболее нагруженном вентиле j -го плеча:

P T ( AV ) j ⁽ T ) , если 0 - ^T Tji < ^A t T2 ;

P Tj ⁽ T ⁾ = 1 P RQ ( AV ) j ⁽ T ⁾ , если ^A t T2 ^{- T} Tji < ^A t T2 ^{+ A T} ; 1 0, иначе,

где τ _T j _i – угол положения анализируемой точки относительно момента включения вентиля на оси времени; A t _T2 - проводящий интервал вентиля.

По аналогии запишем обобщенное выражение для расчета мгновенных значений ТПС вентиля:

0 ( T ) = J⁰ a ^{+ AQ} Tj ( T ) , если ^T Tji * ^A t T2 ^{+ A T} ;

^T j ¹    1® a + A® Tj ( T ) + A® Tj max ( T ) , иначе.

В отличие от режима форсировки в предшествующем уставившемся режиме СГ и в начальный момент КЗ расчет ТПС вентилей можно выполнить по непрерывным зависимостям, описывающим кривую температуры на каждом интервале работы тиристоров. На рис. 1 кривая мгновен-

RkC

У вкл

• интервал выключения у _выкл ^:

A® _У 0выкл ( t ) = ZZ ^PTj0^Rk k = 1 _V

RkCk t - A tT 1

У вкл

где ^A t T1 =У вкл ^+р Т ;

У вкл

1 - e R k C k

t -A t T1

1 - e R k C k

+

+

У вкл

1 - e R k C k

1 - t 1

+ A® Tj 0min k e ^{R k}C^k

)       )

• интервал запирания t_R Q

m

^A® Tj 0зап ( t ⁾ = Z ^PRQj 0 ^Rk ^k = 1 V

t -A t t2 — 1 - e ^r. c .

+

^PTj 0 ^Rk

' R k C k

У вкл V

У вкл

1 - e R k C k

Увыкл eRkCk -1

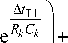
₊ R k C k

^У выкл

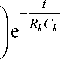
A

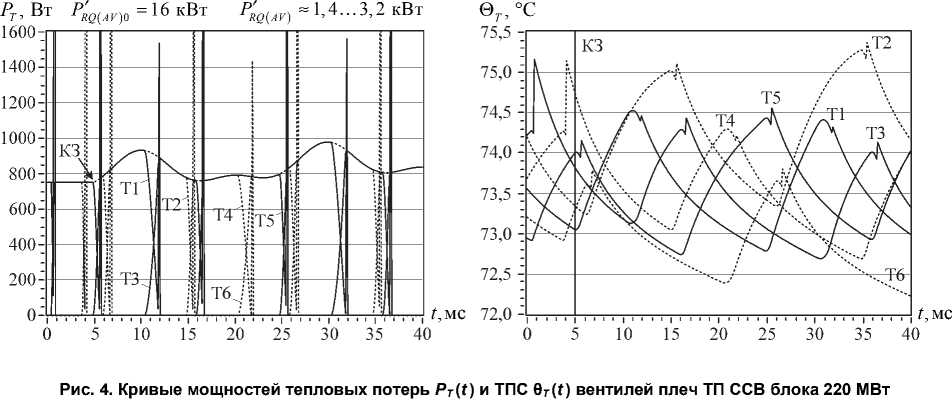
в начале форсировки двухфазного КЗ за повышающим трансформатором (4xT353-800-32 в плече, K H = 1,1)

• непроводящий интервал:

m

^® Tj 0неп ( t ⁾ ” X P T 0 R k

RC

k - I

RkC

У выкл.

V

^A t T1

У вкл.

V

^у вкл.

1 - e R k C k

+

^У выкл

e

R k C k _ i e R k C k

₊ P RQj 0

^PTj 0

t_{RQ e} R k C k

^^^^^^в

V'2 '

e R k C k

+

t

I

RkCk

^{+ AW} Tj 0min k I ^e

.

Формула для расчета величины ΔΘ Tj 0 min и ее слагаемых, входящих в приведенные выражения, получается путем последовательной подстановки указанных выше зависимостей друг в друга:

m

^A® T '0min ^- X’ k - 1

^PTj 0 ^Rk T

RC

R k C

_e R k C k

У выкл

- 1

У вкл

V

^A T1

У выкл

e

_: Rk C k - 1 e R k C k

^У вкл

1 - e R k C k

₊ P RQjO

^PTj 0

+

^t RQ _e R k C k

^^^^^^B

A t T2 _e R k C k

A

,

где Т – период промышленной частоты.

Совмещая зависимости, запишем формулу для расчета мгновенных значений ТПС в момент КЗ:

^А® У 0вкл ( t ) , ⁿ P ^{U 0} <  t <У вкл ;

^А® У 0откр ( t ) , пР ^{И У} вкл <  t < ^{A t} T1^;

® Tj -0 ( t ) -® a + ^

^А® У '0 выкл ( t ) , пРИ ^A t T1 <  t < ^A t T2 ;

^А® Т '0зап ⁽ t ⁾ , ^{при A} t T2 <  t < ^A t T2 ⁺ t RQ ^;

^A0 Tj 'OHen ( t ) , пр ^{и A} t T2 ⁺ t RQ <  t <  ^T ,

где t – время возникновения КЗ, отсчитываемое от момента включения вентилей -го плеча.

В соответствии с приведенными выражениями в среде NI LabView на ЭВМ была разработана математическая модель СГ с тиристорной ССВ для исследования режимов работы сильноточного

ТП при КЗ в энергосистеме, а также при отказах параллельных вентильных ветвей. На рис. 4 приведены кривые мгновенных значений мощностей тепловых потерь и ТПС вентилей, полученные на модели для генератора ТГВ-200-2М в начале форсировки двухфазного КЗ за повышающим трансформатором ( t = 35 мс c шагом Δ Т = T/72). Из анализа кривых видно, что данная модель позволяет в реальном времени рассчитывать мгновенные значения ТПС тиристоров с учетом влияния на них различных факторов, обусловленных работой как самого преобразователя, так и синхронного генератора и ССВ в целом. В связи с этим уравнения модели могут послужить основной при разработке алгоритмов систем интеллектуального автоматического управления синхронными генераторами.