Моделирование энергетических характеристик электродинамических тросовых систем

Космические тросовые системы - новое и очень перспективное направление развития космической энергетики. Особый интерес представляют электродинамические тросовые системы (ЭТС), которые являются альтернативным источником электроэнергии в околоземном пространстве. Они представляют собой систему космических объектов, соединенных между собой токопроводящим тросом.

При пересечении силовых линий магнитного поля Земли токопроводящим тросом, развернутым с орбитальной станции вдоль местной вертикали, в нем наводится ЭДС, и при замыкании контура по тросу начинает течь ток. Со стороны магнитного поля Земли на трос, по которому течет ток, действует распределенная сила Ампера, которая тормозит движение станции. Вся система в этом случае представляет собой глобальный виток, вырабаты вающий электроэнергию за счет торможения в магнитном поле Земли.

Проводящий трос может быть использован как генератор электроэнергии. При движении троса в магнитном поле, снабженного на концах устройствами контакта с плазмой, в тросе будет индуцироваться ЭДС. Если между тросом и одним из устройств контакта с плазмой поместить электрическую нагрузку, то на ней будет производиться полезная работа. Сила, действующая на трос со стороны магнитного поля, в этом случае будет тормозить движение станции.

Концепция тросовых космических систем представляет следующие уникальные характеристики:

• -    сматывание троса может заменить сложный и дорогостоящий процесс стыковки;

• -    возможна передача энергии или данных по тросу;

• -    на платформе, соединенной тросом с орбитальной станцией, можно проводить научные эксперименты, изолированные от магнитной интерференции и динамических турбуленций, обычно исходящих от работающей космической станции;

• -    развернутый вниз трос может позволить изучение верхних слоев атмосферы Земли;

• -    тросовые космические системы могут позволить корректировать траекторию станции;

• - вращающиеся тросовые космические системы могут создавать на платформе искусственную тяжесть, которую можно регулировать, изменяя расстояние от центра масс системы;

• -    возможно использование тросовой космической системы с токопроводящим тросом для создания дополнительной тяги, т е. использование ее в качестве двигателя.

Для исследования движения тросовой космической системы на орбите использовалась модель с невесомым тросом. Расчеты проводились при допущении, что магнитное поле дипольное. На основе разработанной модели исследовалась динамика движения ЭТС в режиме генерации электроэнергии на экваториальных и наклонных круговых орбитах, а также влияние параметров ЭТС на вырабатываемую электроэнергию при ряде допущений.

• 1.    Предложенная модель рассматривает основные энергетические характеристики ЭТС в точке максимальной мощности без учета нагрузки и при условии протекания по тросу постоянного тока. Это допущение обусловлено тем, что на концах троса происходит непрерывный контакт с окружающей плазмой и по тросу, таким образом, течет постоянный ток, значение которого изменяется в зависимости от положения движущегося троса относительно пересекаемых линий магнитной индукции. Поведение энергетических характеристик ЭТС при подключении нагрузки переменного тока является одним из направлений дальнейших исследований в этой области.

• 2.    На концах троса имеются идеальные устройства контакта с плазмой. Идеальность в данном случае подразумевает малое сопротивление контакторов. Практически сопротивление плазменных замыкателей и полых катодов на обоих концах троса составляет не более 5 % сопротивления всей электрической цепи. Поэтому при моделировании протекания тока по тросу сопротивлением контакторов можно пренебречь.

• 3.    Сопротивление плазмы пренебрежимо мало (0,1-0,3 Ом). При использовании длинных тросов (0,5-10 км) в зависимости от диаметра, сопротивление троса составит в среднем 8-10 Ом. Таким образом, сопротивление плазмы составляет менее 3 % сопротивления электрической цепи и им можно пренебречь.

• 4.    Математическая модель, разработанная авторами, не учитывает изменения плотности плазмы на освещенных и затененных участках орбиты, хотя изменение плотности заряженных частиц ведет к изменению сопротивления плазмы. В данной работе значение тока в точке максимальной мощности сравнивалось с током, который может течь при использовании полых катодов в идеальных условиях при плотности частиц 10¹¹ м^-3.

Математическая модель ЭТС включает в себя две взаимодействующие подмодели - модель генерации электроэнергии за счет торможения в магнитном поле Земли и модель движения системы под влиянием всех внешних сил, действующих на систему В проводимых ранее исследованиях эти две модели рассматривались по отдельности, что не давало целостной картины.

Для аппроксимации магнитного поля Земли при исследованиях можно использовать различные математические модели. Наиболее точную аппроксимацию магнитного поля Земли дают модели с использованием полиномов Лежандра и косого диполя. При незначительном различии в ошибке аппроксимации модель с использованием косого диполя является более простой и требует меньше вычислительных ресурсов.

В данной работе модели генерации энергии и движения системы связаны между собой. Связующим звеном является разработанная модель магнитного поля Земли в виде косого диполя, используемая для определения энергетических характеристик ЭТС, которые, в свою очередь, влияют на динамику движения системы (за счет действующей на трос с током распределенной силы Ампера при взаимодействии с магнитным полем).

На основе разработанных математических моделей предложена методика определения допустимых параметров троса для генерации заданной мощности на орбите.

Математическая модель генерации электроэнергии за счет торможения в магнитном поле Земли, разработанная авторами, отличается от ранее используемой тем, что она определяет энергетические характеристики ЭТС в точке максимальной мощности, использует модель магнитного поля Земли в виде косого диполя и позволяет определить зависимость характеристик системы не только от положения на орбите и параметров троса, но и от времени.

При расчетах энергетических характеристик ЭТС была представлена в виде эквивалентной схемы (рис. 1), последовательно включающей в себя источник ЭДС, генерируемой в тросе, и сопротивление, которое определяется суммой сопротивлений (троса R _тр , контакторов R _К1 и R _К2 , нагрузки R _H и плазмы R _п ).

Максимальную полезную мощность в данной схеме можно получить при равенстве сопротивления нагрузки R _H и внутреннего сопротивления источника, т. е. суммы ^R K1 ^{+ R} тр ^{+ R} К2 ^{+ R} п .

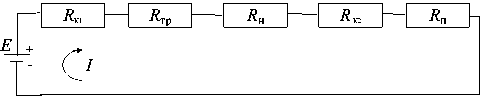
Рис. 1. Эквивалентная схема ЭТС

При допущении, что на концах троса установлены идеальные устройства контакта с плазмой, максималь ная мощность, которую можно получить от ЭТС, опре деляем по формуле

P = ^{E 2} max    4 R _тр ^,

где E - ЭДС индукции, наводящаяся в тросе; R _тр -внутреннее сопротивление троса, вычисляемое по формуле

R _TP =р - ,                  (2)

Тр ps где l - длина троса; S - диаметр поперечного сечения троса; р - удельная проводимость троса.

Учитывая, что длина троса на несколько порядков меньше высоты орбиты, изменением вектора магнитной индукции вдоль троса можно пренебречь и ЭДС индукции, возникающая при его движении в магнитном поле Земли,равна

E = — = BlV , dt

где Ф - поток вектора магнитной индукции через площадь контура; B - вектор магнитной индукции на высоте орбиты основного спутника; V - скорость движения основного спутника.

С учетом выражений (2) и (3) формула для определения максимальной мощности, которую можно получить от тросовой системы (1), принимает вид max

( BlV )²

^4р Уз

= Sl ( BV )².

4 р

Составляющие вектора скорости основного спутника V в точке на орбите определяют по формулам [1]

V n = ^Ы^{p (1} + e • cosW),

V r = VД/ P • e • sin( ^ ),                 ⁽⁵⁾

V = 7 V n + V r ², где V n - составляющая скорости по нормали к радиусу орбиты; V r - составляющая скорости по радиусу орбиты; e - эксцентриситет орбиты, p - фокальный параметр орбиты; $ -угол истинной аномалии; Д -гравитационная постоянная.

Ток, текущий по тросу, в точке максимальной мощности равен

P max

I ² _ .

m

E

На проводник с током, движущийся в магнитном поле, действует распределенная сила Ампера, которую определяют по формуле

F_a = I • B • l • sin( a ), (7) где I -ток, текущий по тросу; a - угол между вектором магнитной индукции и направлением тока.

Сила Ампера отклоняет трос от радиального положения и в зависимости от направления тока в тросе либо ускоряет, либо тормозит движение ЭТС. При больших токах гравитационный момент не может уравновесить момент амперовых сил, и тросовая система переходит во вращение. Поэтому для поддержания тросовой системы в равновесии на силу Ампера накладывают следующее ограничение [2]:

F_a <  3( m _с + m _т /2) щ ² 1 , (8) где m _с - масса субспутника; m _T - масса троса; щ = / Д/ з - угловая скорость основного спутника.

R 0 ³

Ограничение на силу Ампера эквивалентно ограничению на силу тока, текущего в тросе, и, следовательно, на вырабатываемую мощность. Согласно формулам (7)

• и (8), критический ток определяется по выражению

I = 3( m c + mJ3V_          (₉)

^K       B sin( a )

Притоке I <  I _K ЭТС будет оставаться в равновесии.

Основным показателем эффективности ЭТС является отношение генерируемой электроэнергии к массе ЭТС

K _TP

P mTC

(Ю)

где P - мощность, вырабатываемая ЭТС; т^-, - масса источника электроэнергии, которую определяют как сум му масс mTC  mTP + mпк + mмв ,

где m пк - масса плазменных контакторов; m mb - масса механизма выдвижения.

Массу троса определяем по формуле mTP =РmlS + mu ,               (12)

где рm - плотность материала, из которого изготовлен проводник, mu - масса изоляции троса.

Введя параметр m _с = m _тр + m _пк + m _мв + m u по выражениям (4) и (9).. .(13), получим

K TP

^S l ( BV )²

P   4 р

-----=-------------.

^m TC р m^{lS +} m e

Следует отметить, что если в (13) принять р _mlS >>  m _с , то коэффициент K _TP не зависит от длины и диаметра троса.

Генерация электроэнергии ЭТС вызывает снижение орбиты основного спутника. Причем на более низких орбитах генерируется большая мощность, но и снижение орбиты при этом также увеличивается. Определим критерий эффективности использования ЭТС в режиме генерации электроэнергии и назовем его высотно-мощностным К„..:

BM

P кBM =     ,                 (14)

H ₀

где P_max - максимальная генерируемая мощность, кВт; H 0 - относительный уход с орбиты (потеря высоты за сутки в метрах по отношению к высоте орбиты в километрах).

С точки зрения данного критерия использование ЭТС в режиме генерации наиболее эффективно, когда при вырабатывании некоторой мощности относительное снижение ЭТС является минимальным либо при заданном снижении возможна генерация максимальной мощности. В общем случае данный коэффициент зависит от параметров орбиты и троса.

Движение центра масс ЭТС относительно геоцентрической системы координат определяется суммой гравитационных и аэродинамических сил, сил реакции связи, электростатическими и магнитными силами, силой светового давления, возмущениями плазмы и т. д. Центр масс системы принимается совпадающим с центром масс основного спутника, так как масса основного спутника значительно превышает сумму масс троса и субспутника. Задача изучения движения объектов является чрезвычайно сложной, поэтому приходится вводить ряд упрощений и рассматривать, в первую очередь, влияние наиболее существенных факторов, которыми являются грави- тационные, аэродинамические и электромагнитные силы, а также силы реакции связи.

Превалирующей из всех сил в свободном полете является сила, обусловленная гравитационным полем Земли, которая и определяет при заданных начальных условиях траекторию полета основного спутника.

При предположении, что поле тяготения Земли является центральным (гравитационная сила в любой точке направлена к центру Земли), ее величина определяется следующим выражением:

Р ₌ц ^т З m OC

F A   ^ r

где Р _Д - гравитационная сила; r -расстояние от центра масс связки до центра Земли; т _З - масса Земли; m OC -масса объекта связки.

На каждый объект ЭТС кроме гравитационных сил действует также центробежная сила. Центробежная сила определяется следующим выражением:

С = т^¹ R, (16) где C - центробежная сила; m 0 - масса объекта; щ -угловая скорость объекта; R - расстояние от объекта до центра Земли.

Силу сопротивления при движении объекта в молекулярном потоке газа можно рассчитать по формуле

6 = AS m '"hV , (17)

где 6 - аэродинамическая сила; A x - безразмерный коэффициент аэродинамического сопротивления (для тел сферической формы A x = 2...2,5 ); S_m - площадь миде-лева сечения объекта; р ( h ) - плотность воздуха.

Трос, соединяющий объекты связки, ограничивает их свободное движение, поэтому движение связанных объектов будет отличаться от того, какое они имели бы под действием тех же сил в отсутствии троса. Эффект действия троса аналогичен действию сил, вследствие чего действие троса можно заменить силами реакции связи.

Сила реакции идеальной невесомой связи, действующей на объекты, равны по величине и противоположны по направлению. Вектор силы реакции, приложенной к объекту массой m , на оси орбитальной системы коор динат определяется следующим выражением:

m + m

Ri =-λ ij mi ri,

где R i - сила реакции троса; r i - расстояние от объекта до центра масс связки; % - множитель связи; m i - масса i -го объекта.

При допущении, что центр масс связки движется по круговой орбите с постоянной скоростью, множитель связи определяется формулой

% = mm _З щ 2 d , m ₁ + m ₂

где D - текущее расстояние между объектами связки; щ - угловая скорость движения объектов связки.

При допущении, что трос всегда находится в натянутом состоянии (D = l), сила реакции троса будет равна

R i = — m i ' 3 ® ² Dr .

Математическая модель абсолютного движения объектов связки представляет собой следующую систему дифференциальных уравнений:

m.dTr = F i + R i , (21) dt ²

где F i - сумма всех внешних сил, действующих на i-й объект связки.

Таким образом, полученные математические выражения для расчета энергетических характеристик ЭТС в точке максимальной мощности позволяют определить зависимость характеристик системы не только от положения на орбите и параметров троса, но и от времени. Кроме того, получены математические выражения для определения параметров троса, при которых ЭТС будет генерировать заданную максимальную мощность при ограничении на напряжение.

Основными энергетическими характеристиками ЭТС являются максимальная мощность, вырабатываемая системой; наводящаяся в тросе ЭДС индукции; ток в тросе. Кроме того, важными характеристиками работы ЭТС в режиме генератора являются сила Ампера, действующая на трос с током и тормозящая систему; уход системы с орбиты за счет торможения в магнитном поле Земли и коэффициенты эффективности.

На основе разработанных авторами математических моделей проведены исследования энергетических характеристик ЭТС в режиме генерации электроэнергии в зависимости от параметров орбиты и троса с использованием модели косого диполя магнитного поля Земли.

По результатам моделирования определена зависимость максимальной мощности ЭТС от высоты орбиты основного спутника при различных длинах и диаметрах троса (рис. 2).

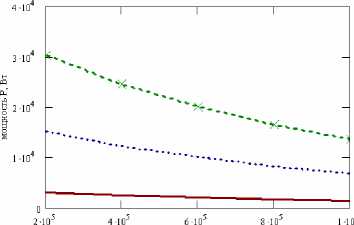
высота орбиты Н, м

L=10km

Рис. 2. Зависимость генерируемой максимальной мощности ЭТС от высоты орбиты для тросов различной длины

Исследования показали, что при увеличении высоты орбиты на 50 км максимальная мощность вырабатываемой электроэнергии уменьшается в среднем на 5 % для любого из выбранных диаметров троса на всем исследуемом интервале высот орбиты 200-1 000 км. Исследования для других параметров троса на этом же диапазоне высот показали аналогичные результаты.

Исследование ЭДС индукции, наводящейся в тросе, при его движении в магнитном поле Земли показало значительную зависимость от высоты орбиты ЭТС (рис. 3).

Анализ полученных зависимостей показал, что при увеличении высоты орбиты на 50 км ЭДС индукции уменьшается в среднем на 2,48 % для любой из выбранных длин троса на всем исследуемом интервале высот орбиты ЭТС и составляет 214 В на высоте 250 км и 147 В на высоте

1 000 км для троса длиной 1 км.

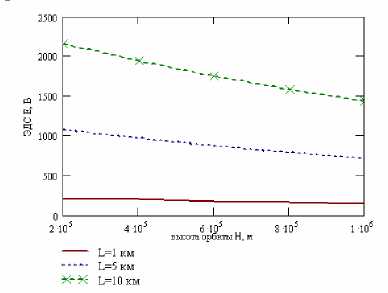
Рис. 3. Зависимость ЭДС, наводящейся в тросе, от высоты орбиты ЭТС для тросов различной длины

На основе математической модели определялся ток в точке максимальной мощности, и проведено исследование его зависимости от высоты орбиты ЭТС (рис. 4)

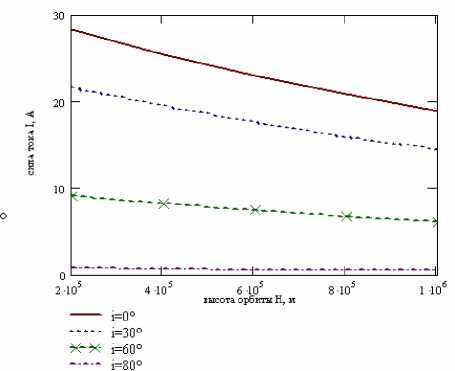
Рис. 4. Зависимость силы тока в тросе от высоты орбиты ЭТС с разным наклонением при длине троса 1 км и диаметре 3 мм

Исследования показали, что ток в точке максимальной мощности с увеличением высоты орбиты на 50 км уменьшается в среднем на 2,5 % для тросов с любыми параметрами из заданного диапазона на всем интервале высот орбиты. При отсутствии орбитального наклона ток в точке максимальной мощности составляет 76,2 А на высоте 250 км и 52,4 А на высоте 1 000 км для тросов диаметром 5 мм и соответственно 27,4 А и 19 А при диаметре 3 мм.

Сила Ампера, действующая на трос с током, зависит от высоты орбиты ЭТС, так как значение вектора магнитной индукции уменьшается с увеличением высоты, и скорость спутника зависит от параметров орбиты. Исследования зависимости силы Ампера от высоты орбиты при ее нулевом наклонении показали, что при увели чении высоты орбиты на 50 км сила Ампера уменьшается в среднем на 4,5% и составляет 2,21 Н на высоте 200 км и 1,05 Н на высоте 1 000 км при длине троса 1км и диаметре 5 мм и соответственно 0,794 Н и 0,376 Н при диаметре 3 мм (рис. 5).

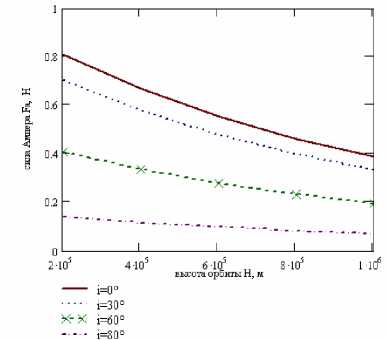
Рис. 5. Зависимость среднего значения силы Ампера, действующей на трос с током, при длине троса 1 км и диаметре 3 мм на орбитах с разными наклонениями

В реальной ЭТС суммарная масса контакторов, механизма съема энергии и механизма выдвижения ориентировочно составляет 10 кг При этом условии проведены исследования зависимости коэффициента эффективности К SEP от высоты орбиты ЭТС при разных параметрах троса (рис. 6, 7).

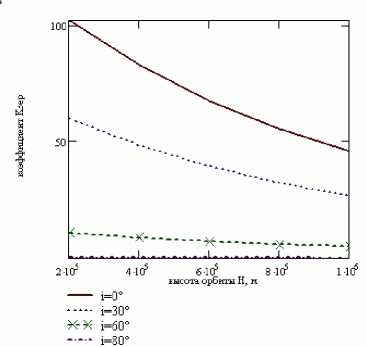
Рис. 6. Зависимость среднего значения коэффициента эффективности К SEP от высоты орбиты ЭТС при длине троса 1км и диаметре 3 мм на орбитах с разным наклонением

Исследования показали, что при увеличении высоты орбиты ЭТС на 50 км К SEP уменьшается в среднем на 4,9 % и для троса длиной 1км и диаметром 3 мм составляет 90,7 на высоте 200 км и 40,58на высоте 1000 км, для тросов длиной 5 км К SEP соответственно равен 117,7 и 52,7.

Таким образом, по результатам проведенных исследований, можно сделать следующие выводы:

• -    при разработке математической модели ЭТС модель генерации электроэнергии за счет торможения в магнитном поле Земли и модель движения системы под влиянием всех внешних сил, действующих на систему, необходимо рассматривать взаимосвязанно;

• -    полученные математические выражения для расчета энергетических характеристик ЭТС в точке максимальной мощности позволяют определить зависимость харак-

• Рис. 7. Зависимость среднего значения коэффициента эффективности КSEP от высоты орбиты при различной длине троса и диаметре 3 мм на орбитах с разным наклонением

теристик системы не только от положения на орбите и параметров троса, но и от времени;

• -    использование ЭТС в режиме генерации электроэнергии наиболее эффективно, когда при генерации некоторой мощности относительное снижение системы минимально либо при заданном снижении возможна генерация максимальной мощности;

• -    математическая модель позволяет определить параметры троса, при которых ЭТС будет генерировать заданную максимальную мощность при ограничении на напряжение и область наиболее эффективного использования ЭТС в качестве источника электроэнергии космического аппарата.