Моделирование кинематической схемы последовательной обтяжки оболочек двояковыпуклой формы на обтяжном прессе FEKD

зуются названные операции, приведена на рисунке 1, где показаны: каретки пресса, которые могут перемещаться по направляющим станины с помощью приводных винтовых пар 2; поворотная плита 3, на которой шарнирно закреплены “балансир” с зажимными устройствами 4 и цилиндр поворота балансира 5; рабочий стол 6 с двумя цилиндрами привода 7; обтяжной пуансон 8 и обтягиваемая листовая заготовка 9.

Аналитический метод построения управляющих программ основывается на результатах теоретической аппроксимации продольного формообразующего контура обтяжного пуансона, кривых перемещения краев листовой заготовки относительно формообразующего контура и на результатах расчета оптимальных технологических режимов, например, с использованием математической модели процесса формообразования обтяжкой оболочки двояковыпуклой формы. Последующий синтез результатов этих расчетов позволит получить оптимальную управляющую программу для ЧПУ пресса.

Первоначальным этапом в расчете движений исполнительных органов пресса FEKD является определение исходных данных элементов пресса FEKD, для которых будет произведен расчет, а именно перемещения балансиров с зажимами и стола пресса с обтяжным пуансоном. Так как обтяжной пуансон является прототипом детали, то геометрические параметры оболочки можно рассматривать так же как размеры пуансона (рис. 2).

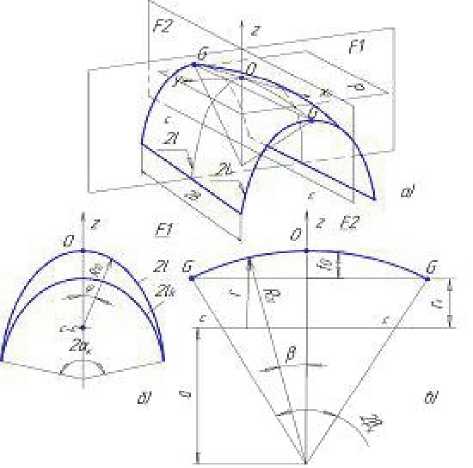
Рис. 2. Оболочка двойной кривизны двояковыпуклой формы

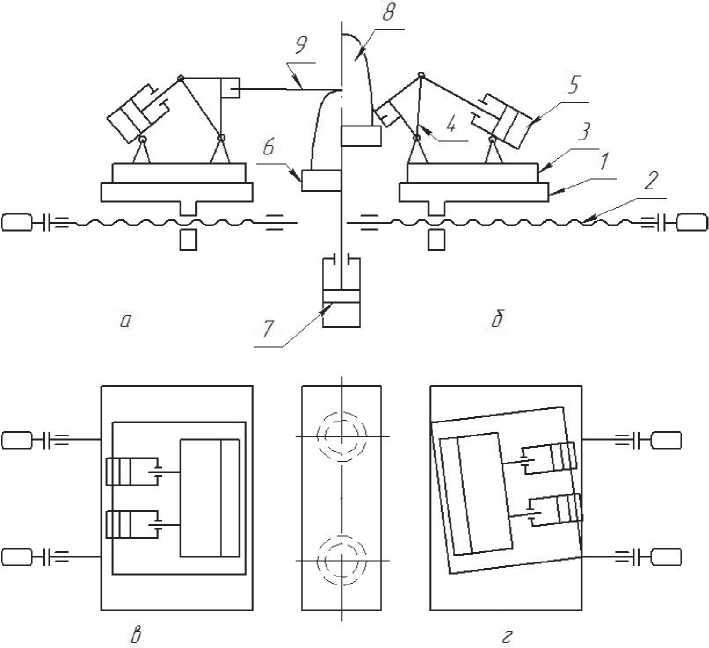
Рис. 1. Различные положения элементов пресса FEKD:

а – исходное положение нижнего стола и балансира (листовая заготовка натянута и касается верхнего гребня пуансона в районе “полюса”); б – конечное положение нижнего стола и балансира

(конец процесса обтяжки); в – установка зажимов при обтяжке деталей из прямоугольных заготовок; г – установка зажимов при обтяжке конических деталей

При этом радиусы главных кривизн линий контуров, пересекающихся в “полюсе” поверхности оболочки (точка О ) соответственно равны: продольный по формообразующему контуру R _{1 о} = 766 мм, а поперечный по второй кривизне R _{2 о} = 9187, 6

мм. Прогиб поперечного контура оболочки в точке О равен f ( O ) = 71 мм. Длина формообразующего контура обтяжного пуансона равна 2616 мм, а ширина листовой заготовки равна 2280 мм.

Геометрические параметры балансира и стола пресса FEKD в исходном положении показаны на рис. 3, а именно: начальное положение штока гидроцилиндра поворота балансира S0, осей от центра вращения балансира до соответствующих элементов (центры радиусов закругления верхней губки и “клюва” S1 и S2, центры головки штока и поворота гидроцилиндра S3 и S4, упора для заправки листа в зажим S5, от оси S5 до радиуса закругления губок), а также угловые параметры соответствующих расстояний S3 и S4 от горизонтали, проходящей через центр вращения балансира F10и F20.

Геометрические параметры балансира и стола пресса FEKD в текущем положении показаны на рис. 4, где изменяют значения положение S0, оси S3 и S4 и углы F10 и F20 на F1 и F2. Были получены необходимые кинематические соотношения между геометрическими параметрами балансира и стола пресса для трех положений листовой заготовки: лист лежит на нижней губке, лист огибает верхнюю губку и лист касается и

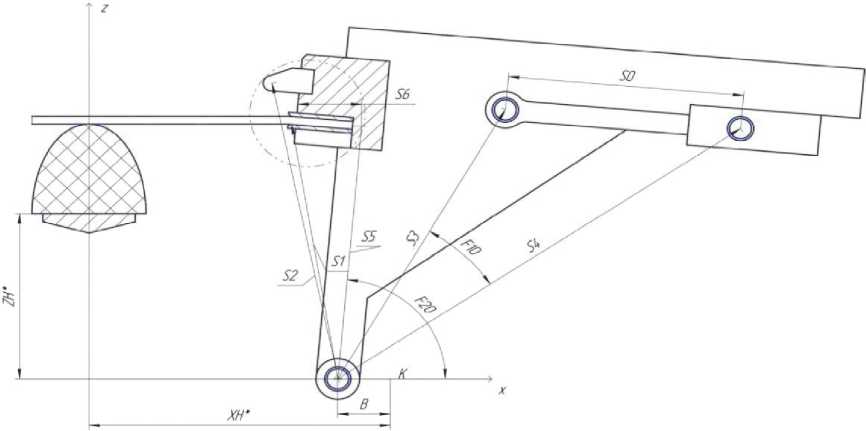
Рис. 3. Геометрические параметры балансира пресса FEKD (исходное положение стола и балансира пресса)

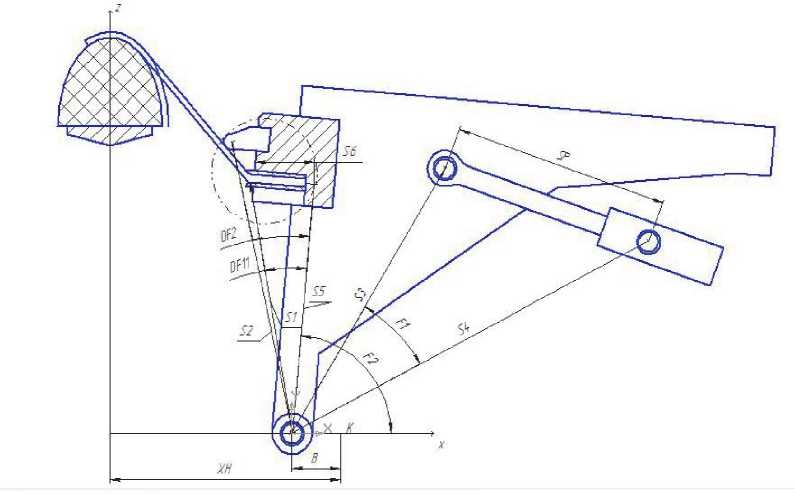
Рис. 4. Геометрические параметры балансира пресса FEKD (текущее положение стола и балансира пресса в процессе обвертки обтяжного пуансона)

огибает “клюв” балансира. Данные соотношения приведены в [2], а для удобства и ускорения расчетов используем электронные таблицы Microsoft Excel (рис. 5). Расчеты были выполнены для пресса FEKD 550-1100 с длиной зажимных губок 3000 мм.

Наиболее важными из всех расчетных данных для начала процесса обтяжки являются исходная высота подъема стола ZH* и начальная позиция каретки балансира XH* при горизонтальном положении листовой заготовки после заправки ее в зажимы пресса и растяжении порядка 0,5% (см. рис. 3).

После определения начального положения балансира и стола пресса FEKD можно переходить к непосредственному расчету величин пе- ремещений рабочих органов пресса в процессе обтяжки листовой заготовки по разрабатываемой кинематической схеме, которая предполагает определенную последовательность операций обтяжки, разделенных разгрузкой и разгибанием с разверткой тонколистовой оболочки. Первоначальным этапом в моделировании кинематической схемы последовательной обтяжки является подготовка геометрических моделей элементов, участвующих в процессе: заготовки, оболочки, обтяжного пуансона, а также основных элементов пресса FEKD, которые имеют непосредственное отношение к формуемой заготовке. Построение и сборка геометрических 3D моделей пресса FEKD и различное положение его элементов выполнялось в Solid Works.

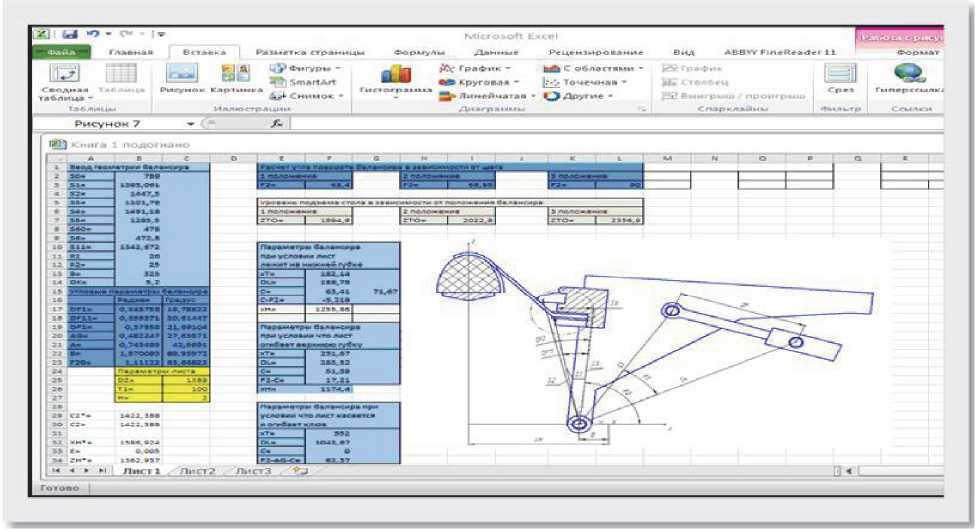
Рис. 5. Вид окошек автоматизированного расчета Excel величины перемещений рабочих органов пресса FEKD

В предполагаемой кинематической схеме последовательной обтяжки выполняются друг за другом два этапа формообразования на одном и том же обтяжном пуансоне и на одном и том же прессе с программным управлением типа FEKD при установке зажимов пресса для обтяжки прямолинейной листовой заготовки:

Одним из основных требований, предъявляемых к этому способу, является раздельное и последовательное осуществление этапов формообразования, разделенных разгрузкой без освобождения детали из зажимов пресса.

На рисунке 6 представлен первый этап формообразования - схема предварительной обтяжки после обвертки плоской листовой заготовки обтяжного пуансона по формообразующему контуру на полный угол охвата а к равным 90 0 . На первом этапе листовая заготовка 1 закрепляется в неподвижных прямолинейных зажимных устройствах 4 и изгибается на полный угол охвата а к обтяжного пуансона 2 за счет синхронизации движений балансиров и стола пресса типа FEKD (рис. 6а). Затем выполняется обтяжка за счет подъема стола пресса 3 при неподвижных балансирах для получения геометрической формы участка оболочки в районе центрального поперечного сечения, проходящем через “полюс” детали в окрестности точки А , но желательно без избыточного деформирования плоского участка схода листовой заготовки с обтяжного пуансона (рис. 6б). На рис. 6в и 6г показаны два вида: штриховой линией – изгибание листовой заготовки с охватом обтяжного пуансона; сплошной линией – окончание предварительной обтяжки.

Избыточное деформирование при простой обтяжке деталей оболочек значительной двойной кривизны двояковыпуклой формы связано с тем, что формообразование в различных сечениях под углом б заканчивается не одновременно. При этом процесс формообразования в сечениях ближе к “полюсу” детали сопровождается избыточным деформированием плоского участка схода листовой заготовки с обтяжного пуансона согласно формуле:

е и = ⁽ е 0 ^{- e}H^)eX P ^{(f a} k / ^П) , ⁽¹⁾ где е_и – деформация на стадии избыточного деформирования плоского участка схода листовой заготовки с обтяжного пуансона под углом б_к после получения двояковыпуклой формы в районе “полюса”, соответствующей полному прогибу центрального поперечного сечения детали оболочки;

е₀ –деформация после формообразования двояковыпуклой формы в районе “полюса” детали, соответствующей полному прогибу центрального поперечного сечения детали оболочки;

е_н - деформация на стадии нестационарного формообразования двояковыпуклой формы в районе “полюса” детали, соответствующей неполному прогибу центрального поперечного сечения, до момента избыточного деформирования плоского участка схода листовой заготовки с обтяжного пуансона;

f – коэффициент внешнего трения;

п – константа упрочнения материала листовой заготовки.

Это вполне достижимо на стадии нестационарного деформирования, несмотря на влияние

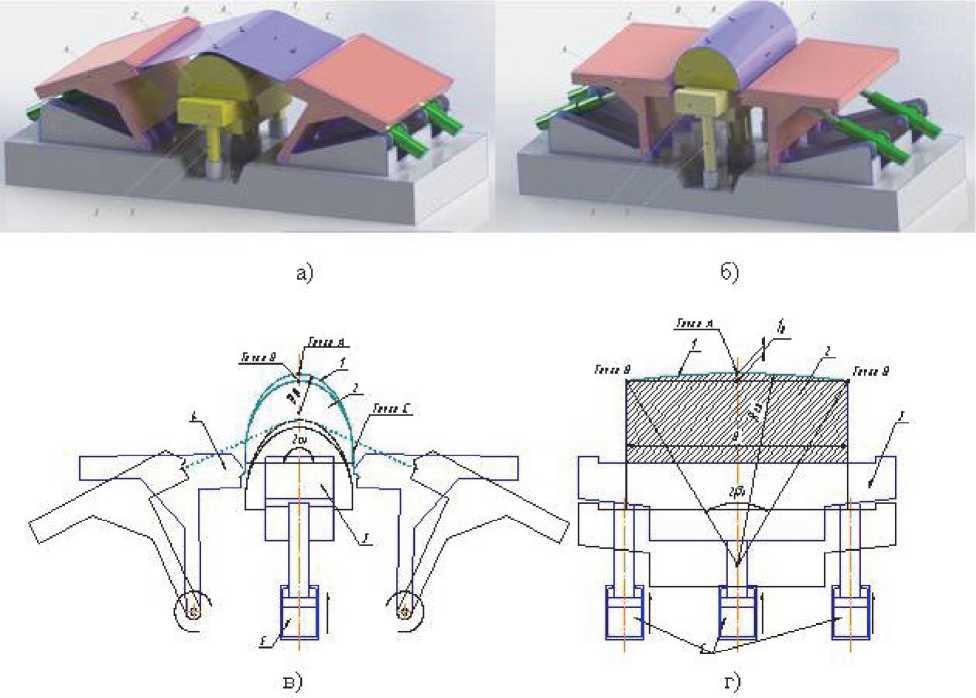
Рис. 6. Схема предварительной обтяжки после обвертки плоской листовой заготовки обтяжного пуансона по формообразующему контуру на полный угол охвата б _к равным 90⁰

внешнего трения при обтяжке тонколистовой оболочки значительной двойной кривизны двояковыпуклой формы. Для оболочки значительной двойной кривизны двояковыпуклой формы при наличии плоского участка схода листовой заготовки с обтяжного пуансона и пресса типа FEKD, имеющего прямолинейный ряд зажимных устройств согласно формуле (1) вероятнее всего избыточная деформация е_и участка схода листовой заготовки с обтяжного пуансона в окрестности точки С несколько меньше или больше деформации формообразования е₀ оболочки двояковыпуклой формы в районе “полюса” детали.

Для обеспечения предварительной обтяжки на полный угол а к равный 90 0 зажимы балансиров 4 пресса сближаются по программе к столу 3 пресса без растяжениялистовой заготовки, которая деформируется при подъёме стола 3пресса за счёт гидроцилиндров 5. Полученная двояковыпуклая форма детали оболочки соответствует продольному и поперечному радиусам R₁₀ и R₂₀ главных кривизн линий контуров, проходящих через “полюс” в окрестности точки А и связанных соотношением через гауссову кривизну К₀ :

R 20 “

К 0

^R 10 ^,

где К₀ полностью определяется коэффициентами первой квадратичной формы поверхности второго порядка, а коэффициенты первой квадратичной формы поверхности определяет ее внутреннюю геометрию, т.е. при переходе от некоторой поверхности к другой поверхности путем только изгибания детали оболочки, при которой длины нанесенных на ней линий сохраняются, коэффициенты первой квадратичной формы поверхности и, следовательно, и гауссова кривизна остаются неизменными [6].

В способе предлагается разгрузить деталь оболочки после предварительной обтяжки и, не освобождая ее из зажимов пресса, осуществить ее разгибание на угол а р , например, равным 15 0 за счет синхронизации движений балансиров и стола пресса FEKD по расчетной траектории. Гауссова кривизна при разгибании поверхности в свободном состоянии сохраняет свое значение, хотя главные кривизны в “полюсе” в окрестности точки А будут меняться. Это понятие играет важную роль в теории тонких оболочек.

На рис. 7а представлено свободное разгибание с разверткой поверхности оболочки после ее разгрузки за счёт синхронизации движений балансиров и стола пресса по соответствующей программе с угла а к равным 9 00 на угол а р, на- пример, равным 150. В результате получим, так называемую изометрическую форму поверхности оболочки по отношению к поверхности обтяжного пуансона с радиусами кривизны в “полюсе” в окрестности точки А соответственно R’1о и R’2о, связанных соотношением при постоянном значении самой гауссовой кривизны К0:

R' = 1 „

2o к R ' , (3) o 1o где, если R1o при разгибании на угол ар увеличивается до R’1o, то R2о, наоборот, уменьшается до R’2о, а поверхность оболочки отступает от поверхности пуансона в районе центрального сечения на величину fр, касаясь обтяжного пуансона только боковыми свободными участками в окрестности точки В.

На рис. 7б представлен второй этап формообразования - схема последующей обтяжки детали оболочки изометрической формы с угла разгиба а р . На рис. 7в и 7г показаны два вида: штриховой линией – разгибание с разверткой поверхности оболочки; сплошной линией – окончание последующей обтяжки.

В результате при последующей обтяжке детали оболочки с изометрической формой повер- хности с угла бр обеспечивается растяжение боковых практически недеформируемых участков листовой заготовки, которые касаются поверхности обтяжного пуансона. В результате растяжения боковые свободные участки заготовки начинают прилегать к поверхности обтяжного пуансона. Данное растяжение сопровождается утонением этих участков, и создаются условия выравнивания толщины оболочки в поперечном направлении до момента неполного прилегания поверхности участка “полюса” оболочки к поверхности обтяжного пуансона.

На рис. 8а представлено свободное изгибание детали оболочки с окончательным охватом обтяжного пуансона после ее разгрузки до полного прилегания поверхности оболочки к поверхности обтяжного пуансона за счёт придания ей изначальной изометрической формы при постоянном значении самой гауссовой кривизны К₀ и при обратной замене значений радиусов R₁₀ и R₂₀ главных кривизн контуров, проходящих через”по-люс” в окрестности точки А за счёт синхронизации движений балансиров и стола пресса по соответствующей программе с угла а р , примерно, равным 15 0 на угол а к равным 90 0 с конечной фиксации геометрической формы детали оболоч-

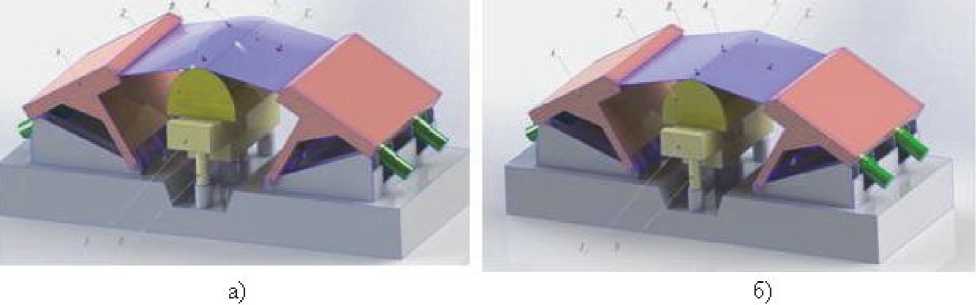
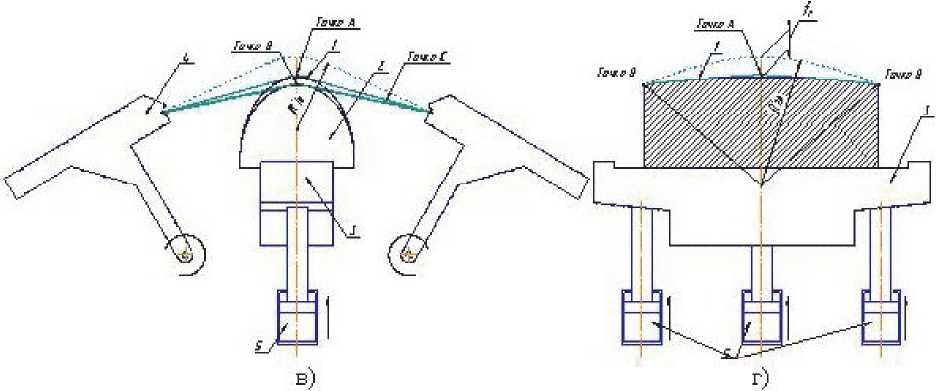
Рис. 7. Схема свободного разгибания с разверткой поверхности оболочки после ее разгрузки и последующей обтяжки детали оболочки изометрической формы с угла разгиба

ки (рисунок 8б). На рис. 8в и 8г показаны два вида: штриховой линией – повторное изгибание листовой заготовки с охватом обтяжного пуансона; сплошной линией – окончание формообразования при последовательной обтяжке.

При этом избыточное деформирование других участков готовой детали оболочки, постепенно прилегаемых к поверхности обтяжного пуансона 2 будет отсутствовать. В результате поверхность оболочки будет соответствовать поверхности обтяжного пуансона, соответствующей изначальной изометрической форме с гауссовой кривизной в точке А, равной произведению R₁₀ и R₂₀ без локализации растяжения на свободном участке заготовки между пуансоном 2 и зажимными устройствами балансиров 3 пресса.

Деформация, которая обеспечивает получение двояковыпуклой формы детали оболочки в районе “полюса”, соответствующей полному прогибу центрального поперечного сечения детали оболочки, равна:

прогиб поверхности оболочки в центральном поперечном сечении, равный f ₀ = R 2_o ( 1 - cos Р к ) , где R₂₀ – поперечный радиус главных кривизн линий контуров, проходящих через “полюс” в окрестности точки А, а Р к - поперечный угол охвата пуансона при формообразовании второй кривизны.

В результате разгибания радиус R _{1 о} увеличивается до значения R^’ _{1 о} , а радиус R _{2 о} , наоборот, уменьшается до значения R^’ _{2 о} при сохранении гауссовой кривизны К₀ , т.е. R ₀₁ • R ₀₂ = К ₀ . “Полюс” оболочки1 в окрестности точки А приподнимается над поверхностью обтяжного пуансона 2 на величину f _р. Эта величина определяется из формулы 5 при условии равенства значений деформаций е₀ и е_А :

^е 10

ln

( R 10

к  4 R^f p- ] ■       (5)