Моделирование кинематики медицинского манипуляционного робота типа SCARA с учетом непараллельности осей вращения и мaнуального рабочего органа с четырьмя степенями свободы

© 2025 Смирнов Д. Б., Фролов И. А., Воротников А. А., Гринь А. А., Левченко О. В. Ли- цензировано по CC BY 4.0. Чтобы ознакомиться с условиями этой лицензии, посетите сайт

Роботы обладают геометрическими погрешностями, которые являются следствием неточного изготовления деталей и сборке узлов. Для компенсации данных погрешностей могут применяться различные методы калибровки (например, с использованием оптических измерительных систем, таких как лазерный трекер) [1]. Традиционные модели, не учитывающие фактические длины звеньев и их относительное расположение, не пригодны для задач медицинской робототехники.

Вопрос сравнения движений хирурга и роботизированной системы активно исследуется в последние годы. В работах [2–5] показано, что роботизированные комплексы обеспечивают сравнительно лучшие показатели по критериям скорости резания, отклонения от заданной траектории и повторяемости движений. Однако эти исследования сосредоточены на полностью активных системах. В случае гибридных архитектур, сочетающих роботизированное позиционирование с мануальным введением инструмента, подобные критерии требуют пересмотра, поскольку финальная фаза вмешательства остается под контролем хирурга.

В настоящее время существуют решения, где робот управляется хирургом с помощью удаленного пульта управления [6, 7]. Также в современных роботизированных системах для транспедикулярной фиксации, таких как ROSA Spine, ExcelsiusGPS и Mazor X, робот выполняет точное позиционирование направляющей втулки в соответствии с предоперационным планом, после чего хирург вручную вводит инструмент или винт по заданной траектории [8–10]. Здесь же предлагается несколько иной подход, где ориентация задается не роботом программно, а хирургом мануально.

В данной работе рассматривается двухзвенный манипуляционный робот типа SCARA, модифицированный для медицинских задач, с явным учетом непараллельности осей вращения звеньев - фактора, обычно, игнорируемого в традиционных моделях. Особое внимание уделяется интеграции мануального рабочего органа, устанавливаемого через сферический шарнир, который позволяет осуществлять ориентирование рабочий органа вручную, что особенно ценно в условиях операционной.

Целью настоящей работы является разработка и верификация алгоритма решения обратной задачи кинематики (ОЗК) для указанной системы с учетом относительного расположения звеньев и мануального рабочего органа.

Описание конструкции медицинского манипуляционного робота

В данной работе рассматривается медицинский манипуляционный робот, который обладает четырьмя степенями подвижности, предназначенный для проведения операций по транспедикулярной фиксации позвоночника. Его конструкция приведена на рис. 1. Первая и вторая степени подвижности используются для позиционирования в плоскости перпендикулярной оси вращения первого звена, третья и четвертая – для ориентации рабочего органа. Введение хирургического инструмента обеспечивается хирургом мануально в целях повышения безопасности пациента.

С целью упрощения управления и позиционирования манипулятора предлагается не использовать третью и четвертую степени подвижности, с фокусом на первых двух. Так как на механический интерфейс устанавливается рабочий орган со сферическим шарниром, обеспечивающий три степени свободы для задания требуемой ориентации инструменту. Это компенсирует неиспользование третей и четвертой степеней подвижности. Подобный подход позволяет использовать упрощенную кинематическую модель в виде двухзвенного манипулятора с непараллельностью осей.

Кинематическая модель двухзвенного манипуляционного робота с учетом непараллельности осей вращения

Представлена модифицированная кинематическая схема SCARA-манипулятора, где ось вращения второго звена наклонена под углом α относительно оси первого звена на рис. 2. Поскольку первая ось вращения также может быть наклонена относительно вертикали вследствие особенности конструкции (погрешности установки и/или изготовления), то этот случай математически эквивалентен повороту всей мировой системы координат. Для направления оси вращения первого звена n1 по z.

Ввиду этого рассматривается упрощенная модель с наклоном второй оси n2 относительно n1 (на углы a , f0 ( n1 и n2 скрещивающиеся прямые)). Центр первого звена находится в токе P0 , длина первого и второго звена: l1 и l2 соответственно; q1 и q2 – обобщенные координаты.

Рис. 1. А) медицинский манипуляционный робот с четырьмя степенями подвижности: 1 – первая степень подвижности, 2 – вторая, 3 – третья, 4 – четвертая, 5 – сферический шарнир (часть рабочего органа), 6 – мировая система координат (рамка, закрепленная на позвонке), 7 – целевое положение на фантоме с заданной ориентацией, 8 – рамка со светоотражающими маркерами для определения ориентации и положения с помощью навигационной системы, 9 – инструмент, установленный в рабочем органе.

Б) Общий вид системы для проведения хирургических операций по транспедикулярной фиксации позвоночника: медицинский манипуляционный робот закреплен на столе, справа от него – навигационная система

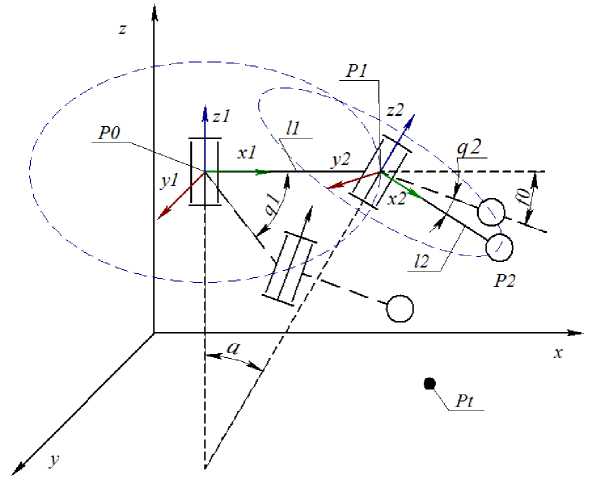
Рис. 2. Кинематическая схема двухзвенного манипулятора с наклонной осью вращения

При q1 = 0 первое звено направлено вдоль оси X . Положение второго шарнира можно выразить как:

Г cos(q1)l P1(q1) = P0 + I1[sin(q1)],

где Р0 = [x0,y0,z0]T.

С вращением первого звена вектор вращения второго звена будет также изменяться:

I sin( a) cos( q1 + /0)1 sin(a) sin(q1 + /0) . cos(a)      J

Начальное направление второго звена (при q 2 = 0):

I cos( a) cos( q1 + /0)1 cos( a) sin( q1 + /0) . -sin(a')      J

Положение конца второго звена может быть выражено с использованием формул (1)-(3):

Р2 = P1(q1) + 12 ■ j2(q1,q2)

где

j2(q1,q2~) = cos(q2} ■ j2 + s in(q2) ■ (n2(q1) x j2),

Г -sin(q1 + /0)1 n2(q1) xj2 = [ cos(q1 + /0) ].

Обратная задача кинематики (ОЗК) для двухзвенного манипулятора с наклонной осью вращения второго звена. Для решения ОЗК используется формула для концевой точки P2, выведенная ранее (4). Для этого необходимо решить систему уравнений:

( x = x0 + 11 cos(q1) + I2(cos(q2) cos(a) cos(q1 + /0) — sin(q2) sin(q1 + /0))

y = y0 + 11 sin(q1) + I2(cos(q2) cos(a) sin(q1 + /0) + sin(q2) cos(q1 + /0)). (5)z = z0 — 12 cos( q2~) sin( a)

Из последнего уравнения системы находим q 2:

q2 = arccos ( z0 f Y

4              \l2sin(a)J

Обозначим ф = q1 + /0, тогда система (5) примет вид:

А = U cos(ф') + V sln(ф) В = —V cos(ф') + U sln(ф') ( z0 — z \    '

arccosl          )

\ I2sin(a)/ где cos( ф — /0) = соз(ф) cos(/0) + sin( ф) sln(f0~), sin(ф — /0) = sln(ф') cos(/0) — cos(ф') sln(/0~), А = х — х0,

В = у — у0,

U = 11 cos(/0) + 12 cos(q2~) cos(a~),

V = 11 sln(/0) — 12 sln( q2~) .

Тогда

„            / UB+AV\ q1 = arctan (AU_BV) — /0.

Мануальный рабочий орган: геометрическая декомпозиция

Поскольку мануальный рабочий орган вводится хирургом вручную, его выдвижение, ориентация могут быть выставлены до перемещения робота с помощью навигационной системы. Это возможно, так как целевая ориентация, положение конца рабочего органа, а также глубина погружения винта предопределены в ходе планирования. Это позволяет декомпозировать задачу.

На рисунке 3 представлена кинематическая схема мануального рабочего органа. Расстояние d между центром сферического шарнира и осью направляющей может быть определено экспериментально с использованием оптической навигационной системы: для этого регистрируются координаты двух точек, лежащих на оси направляющей, после чего вычисляется расстояние от центра шарнира до полученной прямой.

Поскольку на этапе предоперационного планирования заданы целевая точка Pt , единичный вектор требуемой ориентации инструмента v , а также расстояние d , задача сводится к однозначному определению положения точки P 2 точки крепления рабочего органа к манипулятору. Эта точка вычисляется геометрически как положение, из которого инструмент, ориентированный вдоль v и проходящий через направляющую, достигает целевой точки Pt .

Исходя из этого, можно однозначно получить точку Р 2. Используя рис. 3, имеем:

P2 = Pt — d ■ dv — It ■ v . (9)

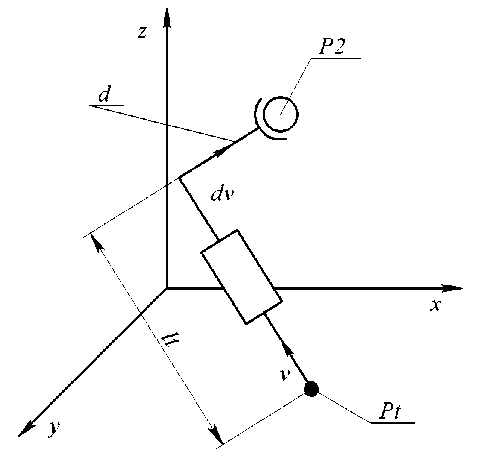
Рис. 3. Кинематическая схема мануального рабочий органа с четырьмя степенями свободы

Использование полученной модели для медицинского манипуляционного робота. Идентификация начальных параметров

Для определения фактических длин звеньев l 1, l 2 и направления осей вращения n 1, n 2 необходимо последовательно вращать звенья, собирая точки с помощью навигационной системы с меток, расположенных на рамке 8 на рис. 1 А). После того как точки получены, проводится аппроксимация плоскостями для каждой оси вращения, что позволяет определить направление векторов осей вращения. Далее аппроксимация окружностью, например, методом наименьших квадратов (МНК) [11, 12]. После чего можно определить центр основания P 0 и длины звеньев ( l 1, l 2).

Центр сферического шарнира определяется экспериментально. Для этого мануальный рабочий орган освобождается от фиксации, после чего в четырех и более различных положениях регистрируются координаты маркеров на рамке 8, с использованием оптической навигационной системы. Полученное множество точек аппроксимируется сферой методом наименьших квадратов; ее центр принимается за центр сферического шарнира.

Определение взаимного расположения направляющей и центра сферического шарнира определяется следующим образом: по двум положениям фиксации рабочего органа вдоль направляющей строится прямая, задающая ориентацию направляющей в пространстве, что позволяет установить её геометрическую связь с центром сферического шарнира. По двум положениям фиксации рабочего органа вдоль направляющей строится прямая, задающая ориентацию направляющей в пространстве, что позволяет установить ее геометрическую связь с центром сферического шарнира.

Информация о целевой точке, требуемой ориентации инструмента и глубине его введения формируется хирургом на этапе предоперационного планирования на основе данных компьютерной томографии. Интраоперационная привязка плана к анатомии пациента осуществляется с помощью оптической навигационной системы, обеспечивающей отображение отклонений текущего положения инструмента от запланированной траектории.

Общий алгоритм применения предложенного метода включает следующие этапы:

• 1.    Идентификация кинематических параметров манипулятора: определение длин звеньев, направлений осей вращения и положения основания с использованием навигационной системы.

• 2.    Идентификация геометрии рабочего органа: определение центра сферического шарнира и ориентации направляющей.

• 3.    Задание целевой конфигурации инструмента: установка требуемой ориентации и глубины выдвижения на основе предоперационного плана.

• 4.    Расчет обобщенных координат манипулятора: решение обратной задачи кинематики и извлечение инструмента из направляющей для безопасного перемещения.

• 5.    Позиционирование манипулятора: перемещение в расчетное положение.

• 6.    Выполнение хирургической манипуляции: повторное введение инструмента в направляющую и его ручное введение в тело пациента в соответствии с запланированной траекторией.

Заключение

В работе предложена и верифицирована кинематическая модель двухзвенного медицинского манипуляционного робота типа SCARA, учитывающая реальные геометрические особенности конструкции. Особенностью предложенной архитектуры является интеграция мануального рабочего органа, закрепленного на сферическом шарнире, обеспечивающем три степени свободы для ручной ориентации инструмента. Разработанный алгоритм решения обратной задачи кинематики учитывает, как геометрию манипулятора с непараллельными осями, так и параметры мануального инструмента, определяемые с использованием оптической навигационной системы. Процедура идентификации геометрических параметров, включая длины звеньев, направления осей вращения, положение центра сферического шарнира и ориентацию направляющей, реализована экспериментально и основана на стандартных методах аппроксимации (метод наименьших квадратов).