Моделирование кинематики пластического течения при формообразовании гофра облегченного фланца

Для авиастроения традиционно актуальным является уменьшение веса при одновременном повышении прочности конструкции, а также сокращение времени на капитальный ремонт воздушных судов. Эту задачу решают в том числе с применением быстроразъемных соединений, реализованных посредством облегченных фланцев (рис. 1) из титановых сплавов. Преимуществами данных соединений являются быстрота, удобство и легкость при многократном монтаже титанового трубопровода, его ремонте или частичной замене [1].

Рис. 1. Облегченные фланцы из сплава ПТ-7М с диаметром условного прохода 90 мм

Процесс формообразования зига облегченного фланца подразделяется на две стадии: штамповка гофра с целью предварительного набора материала в зоне интенсивного пластического формоизменения; калибровка гофра с целью придания ему окончательной формы зига фланца (рис. 2).

Наиболее ответственной является первая стадия штамповки , на которой возможно образование браковочных признаков в виде недопустимого утонения стенки и разрыва материала, поэтому для оценки предельных возможностей процесса была предложена математическая модель кинематики пластического течения в конечный момент формообразования предварительного гофра фланца (рис. 3).

В силу наличия горизонтальной плоскости симметрии будем рассматривать верхнюю половину гофра. В пределах рассматриваемой части облегченного фланца выделим три зоны: I – переходная зона между основной трубой и гофром; II – основная часть гофра; III – вершина гофра.

Для описания геометрии используем следующие системы координат: в зоне I – тороидальную систему координат r , θ , φ ( φ – угловая координата в плоскости, перпендикулярной оси симметрии фланца (на рис. 3 не показана)); в зоне II – цилиндрическую систему координат z , r , φ ; в зоне III – тороидальную систему координат r , θ , φ .

В принятых системах координат границы зон определяются следующими неравенствами [2]:

π зона I: r1 ≤ r ≤ r1 + t; 0 ≤ θ ≤   ; 0 ≤ φ ≤ 2π, зона II: r2 – t ≤ z ≤ r2; R1 ≤ r ≤ R2; 0 ≤ φ ≤2π,

π зона III: r2 – t ≤ r ≤ r2; 0 ≤ θ ≤   ; 0 ≤ φ ≤ 2π.

Поле скоростей, моделирующее пластическое течение в каждой зоне должно удовлетворять соответствующим условию несжимаемости и кинематическим краевым условиям.

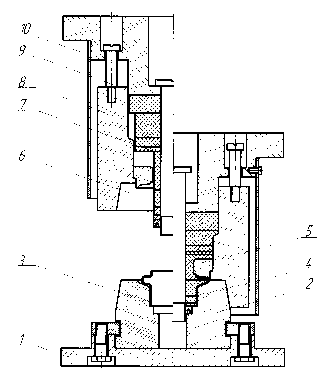
Рис. 2. Схема штампа для калибровки облегченных фланцев: 1 – плита; 2 – нижняя полуматрица; 3 – фланец с предварительным гофр ом; 4 – фланец с откалибр ованным гофром; 5 – верхняя полуматрица; 6 – пуансон эластичный; 7 – прижим эластичный; 8 – корпус; 9 – пуансон жесткий; 10 – крышка

ϕ   R ₂ + r cos θ

( V_r cos θ - V θ sin θ ) ;

1 ∂ V

ε = ( ^θ + V ). θ r

r ∂θ

Компоненты скорости V r и V θ удовлетворять краевым условиям:

V r = 0; V θ = 0.

r = r ₂

Принимаем, что

θ = 0

V_r = r ₂ - r ,

тогда

ε _r

∂ V r

= - 1 .

∂ r

Подставляя (3) в (1), получим

должны

следую-

щее уравнение для определения скорости V θ :

R ₂ + r cos θ

[( r ₂ - r )cos θ - V θ sin θ ] +

1 ∂ V

+ ( ^θ + r ₂ r ∂ θ

- r ) - 1 = 0

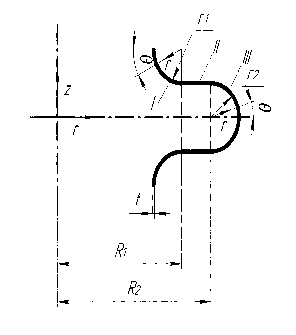
Рис. 3. Конфигурация и геометрические параметры предварительного гофра облегченного фланца : r 1 и r 2 – радиусы кривизны поверхности ручья матрицы

Толщина стенки фланца t является достаточно малой величиной . Поэтому с целью упрощения расчетов в (4) можно принять

r ≈ r ₂ .

С учетом (5) соотношение (4) принимает вид:

∂ V θ      r sin θ

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^   ^^^^^^^   ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

-

∂ θ   R ₂ + r cos θ

⋅ V θ - r = 0 .     (6)

Решение (6) будем искать в виде V _θ = u ⋅ v ,

тогда

∂ u      ∂ v     r sin θ

⋅ v + ( -               ⋅ v) ⋅ u - r = 0.

∂θ     ∂θ R2 + rcosθ

Для формообразования осесимметричных элементов трубопроводов применяют процесс штамповки раздачей со свободным перемещением конца трубной заготовки в жестких разъемных матрицах эластичным пуансоном. В силу осевой симметрии гофра принимаем, что во всех зонах компонента вектора

Принимаем, что

∂ v     r sin θ

-

∂ θ R ₂ + r cos θ

Решая (7), находим

⋅ v = 0.

1 ln v = ln            => v =

R ₂ + r cos θ         R ₂ + r cos θ

Используя v , находим множитель u :

.

скорости V φ = 0, а остальные компоненты тора скорости не зависят от координаты φ . Зона III. Условие несжимаемости данной зоны имеет вид:

ε _r + ε _ϕ + ε _θ = 0,

век-

для

где линейные компоненты тензора скоростей деформации имеют вид

ε

r

∂ v r _;

∂ r

∂ u

⋅-

R ₂ + r cos θ ∂ θ

r = 0,

u = ( R ₂ θ + r sin θ ) r + c ₁ ( r ) .

В итоге скорость V θ равна:

_V = ( R ₂ θ + r sin θ ) r +    c ₁( r )

θ     R ₂ + r cos θ R ₂ + r cos θ

.

Используя краевые условия (2), находим, что c ₁ ( r ) = 0 .

Таким образом, для зоны III будем иметь следующее поле скоростей:

V (3) = r - r ; V (3) = ^{( R} 2 ⁹ + r sin ⁹ ) r . ^{r 2}    ’ ⁹ R ₂ + r cos 9 ’

Vф3) = 0.(8)

Зoʜa II. В зоне II линейные скорости деформации равны:

d V     Vd

Sr = "^r; Еф = -r-; £z = z , о r          r а условие н есжимаемости имеет вид

Sr + Еф + Sz = 0 .

Компоненты поля скоростей должны удовлетворять краевому условию:

Vz| = 0(10)

^z = ^r 2

и условиям неразрывности скоростей между зонами II и III:

V z ⁽²⁾| = V r ⁽³⁾|; V = - V ^.

z = ^R 2     ₉ = П      r = ^R 2      ₉ = П

Для границы между зонами II и III: ( 3 )       ( 2 )

I I .

Подставляя (12) в выражение для будем иметь

V z ⁽²⁾ = ^r 2 ^- z ,

(3) r ,

при этом первое условие (11) и условие (10) будут выполнены.

Из (13) находим d V

Е = — =- 1. ^z d z

Подставив (14) в (9), для определения скорости V _r имеем уравнение:

d V V

—- + — -1 = 0 или drr

-(Vr • r) = r .(15)

о r

Решая (15), получаем

Vr = r+c ‘z’.(16)

2 r

Для определения постоянной интегрирования c ₂ ( z ) используем второе условие (11).

Подставляя в выражение для V 9 ' 9 = ^П и r = z (условие (12)), имеем

V

9 = П

( ^r 2 п + z ) z

R 2

Тогда, используя (16) и второе условие (11), определяем

( ^r 2 П 2 + z ) z

R 2

/ \ n П x    Ri c 2( z) = -(R 2- + z) z - -2".

В итоге для скорости V_r имеем соотношение:

2( R 2 П + z ) z + R 22

V =---2-------- r 22

.

Таким образом, поле скоростей в зоне II описывается соотношением:

2( R 2 П + z ) z + R 2 ²

Vф2) = r2 - z ; V<2) = r--2-;

z 2         r 22

V ф ²⁾ = 0.

Зoʜa I. Для тороидальной системы координат r , θ , φ зоны I условие несжимаемости определяется соотношением:

где

^S r ^{+ Е} Ф ^{+ S} 9 = ⁰ ,

S =dV_ ;

^r d r

^е ф = -—¹—-⁽ V 9 sin ^{9 -} V r cos ⁹ );

R 1 - r cos 9

1 zd V₈      .

S 9 = -( + ^V r ).

r o9

Кинематическое краевое условие для данной зоны имеет вид

V r | = 0, r = r !

а условия неразрывности скоростей на границе между зонами I и II определяются выражениями:

V r <'>| = - V <²>|; V e <"| = V r <²>|.

₉ = П        r = ^R 1       ₉ = П      r = ^R 1

Для границы между зонами I и II:

z ⁽²⁾ = ( r 1 + r ₂) - r ⁽¹⁾

.

Подставляя (21) в выражение для находим из первого условия (20):

V_r ⁽¹⁾ | = r 1 - r .

9 = П

Принимаем для зоны I

Vr = r1 - r, при этом условие (19) будет выполнено.

Из (22) определяем d V

S _r = —- = - 1.

d r

Подставляя (23) в (18) и принимая, как и для зоны III, r = r 1 , для определения скорости V ₉ будем иметь следующее уравнение:

d V₉     r sin 9

—- +-- V_fl - r = 0.

99    R 1 - r cos 9 ⁹

_Vz (2) _,

Пусть v ₉ = u ■ v , тогда (24) принимает вид:

^V θ =

( R 1 9 - r sin 9 ) r

d u    ,5 v     r sin 9

—v + (— +---------v) u - r = 0 .

d9   x9 R1 - r cos 9

Принимаем, что d v     r sin 9

— +--------= 0.

d9 R 1 - r cos 9

Из (26) находим d v      r sin 9

--d9 , v     R 1 - r cos 9

1 In v = In-------------,

R 1 - r cos 9

R 1

-

R 1 - r cos 9

^{- R} 22 ^{- 2( R} 2^ ^{+ r} 2 ) ^r 2 ^{- 2( R} 1 2 ^- r ) r .

-

-

-

v=

R 1 - r cos 9

•

Подставляя (27) в (25), определяем множитель u

d u       1

---= r , d9 R 1 - r cos 9

u = ( R 1 9 - r sin 9 ) r + c ₃( r ).

Таким образом,

Vθ =

( R 1 9 - r sin 9 ) r

R ₁ - r cos 9

+

R 1

Постоянную интегрирования найдем из второго условия (20):

^c 3 ^{( r} )

- r cos 9

c 3 ^{( r} )

•

V (2)| = R - r r=R z = r1 + r2)-r тогда

π

^2[ R 2 2 + ⁽ r 1 + ^r 2 - r ^{)]( r} 1 + ^r 2 - r ) + R 2

2 R

,

,  ( R 1 П - r ) r

V d) =---²-----

θ _R

9 = ^{n          1}

+ c 3 ⁽ г ) = R

R 1    2

-

π

^{2[ R} 2 2 + ^{( r} 1 + ^r 2 ^{- r )]( r} 1 + ^r 2 ^{- r} ) + ^R 2

z.    R²

c 3 ^{( r} ) = —

-

R 2

-

2 R 1

π

^{[ R} 2- + ⁽ r 1 + r 2

,

- r )] ^x

x ^{( r} 1 + r , ^- r ) ^{- (} R 1 П 2 ^{- r} ) ^r .

Таким образом, выражение для скорости v9 в зоне I имеет вид v = (R|9 - r sin9) r

⁹    R - r cos 9

R ^{2 -} R 2 ^- 2[ R 2 ПП ^{+ ( r} 1 ^{+ r} 2 ^{- r )]( r} 1 ^{+ r} 2 ^{- r} ) ^{- 2}( R 1 ПП ^{- r} ) ^r

2( R - r cos 9 )                 "

Принимаем с целью упрощения расчетов r = r ] , окончательно находим:

2( R 1 - r cos 9 )

В результате получено, что пластическое течение в зоне I описывается соотношениями:

V r ⁽¹⁾ = r 1 - r ; v „^{( 1)} = 0;

V (1) = ^{( R} 1 ⁹ - r sin ⁹ ) r -

⁹       R 1 - r cos 9

R 1

-

^{- R} 2 ^{- 2( R} 2 "Г + ^r 2 ) ^r 2 ^{- 2( R} 1 "Г^- r ) r -------------²----------------²------. (28)

2( R 1 - r cos 9 )

На основании полученных результатов (8), (17), (28) кинематика пластического течения при формообразовании предварительного гофра фланца описывается следующими соотношениями.

Зона I:

v r"¹ = r 1 - r ; v „^{( 1)} = 0;

V (1) = ^{( R} 1 ⁹ - r sin ⁹ ) r -

⁹ R 1 - r cos 9

^R 1 ^{- R} 22 ^{- 2( R} 2 — + ^r 2 ) ^r 2 ^{- 2( R} 1 — ^-

-

2( R 1 - r cos 9 ) Зона II:

^vz^№ = ^r 2 ^{- z} ;

v = 0.

Зона III:

v r ⁽³⁾ = r ₂ - r ;

r ) r

.

2( R 2 - + z ) z + R 2

v ( ² ) = L __²____________•

;

^r 2           2 r

V , „ = (^R9 + ^rsin ⁹ ) ^r ;    „ = 0.

R ₂ + r cos 9 ^ф