Моделирование кинетики сверхбыстрого разделения и рекомбинации зарядов в возбужденных цинк-порфиринах

Y Рогозина М.В., Ионкин В.Н., Иванов А.И., 2012

В последние несколько десятилетий все больше внимания уделяется исследованию детальных механизмов сверхбыстрого переноса электрона [1; 5; 13; 14]. Это обусловлено тем, что фотоиндуци-рованный перенос электрона является одним из наиболее распространенных и простейших химических процессов. Перенос электрона лежит в основе огромного числа явлений, происходящих в живой и неживой природе. Интерес к рассматриваемой проблеме значительно возрастает благодаря все более широкому использованию возможностей современной спектроскопии сверхвысокого временного разрешения. В подавляющем большинстве экспериментальных работ исследовался перенос заряда из первого синглетного или первого триплетного возбужденных состояний. Только относительно недавно появились исследования переноса заряда из второго синглетного возбужденного состояния S ₂ и последующей рекомбинации зарядов в первое синглетное возбужденное состояние S ₁ [9; 11; 15; 17; 19]. В этих экспериментах в качестве объектов исследования выступали производные цинк-порфири-нов. В работе [17] были синтезированы и исследованы молекулярные переключатели, которые представляют собой триады, включающие цинк-порфирин и ковалентно связанные с ним два акцептора, расположенные на противоположенных сторонах порфиринового кольца. Параметры триады были выбраны так, что состояния S ₁ и S ₂ тушились переносом электрона на разные акцепторы [17]. Это открывает возможность управления направлением переноса электрона путем изменения длины волны возбуждающего импульса.

1.    Модель сверхбыстрого разделения зарядов из второго возбужденного состояния и последующей рекомбинации зарядов в первое возбужденное состояние

Для описания сверхбыстрого разделения зарядов (CS) из состояния S2 и последующей рекомбинации зарядов (CR) в состояние S1 используется минимальная модель, включающая три электронных состояния: первое и второе синглетные возбужденные состояния |S 1р, |S2р соответственно, и состояние с разделенными зарядами |CSp (рис. 1). Эта модель была предложена ранее и описана в работе [12].

Диабатические поверхности свободной энергии электронных состояний в терминах координат реакции Q _i ( i -я координата соответствует i- й моде растворителя) могут быть записаны в следующем виде [12]:

Q i ²

U S 2   ⁸ 4 Е_п

( n )

U es 8

( Q i" 2 E r )

4 E ri

- ⁺ n h ^{a +} . G cs ,

( m )

U s 1 = 8

-Qi- + mha + G. 2, 4 Eri             ‘ где a и n, m (n, m = 0, 1, 2, ...) - частота и квантовые числа эффективной внутримолекулярной колебательной моды соответственно;

„ G_cs - свободная энергия реакции разделения зарядов из второго возбужденного состояния;

_l G ₁₂-разность свободных энергий между первым и вторым возбужденными состояниями.

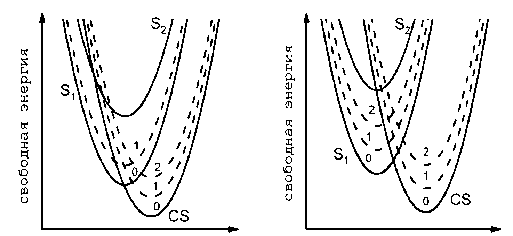
координата реакции         координата реакции

Рис. 1. Схематическое изображение диабатических термов электронных состояний S ₂, CS и S ₁. Пунктирные линии – колебательные подуровни электронных состояний CS и S ₁

Для описания временной эволюции системы применяется стохастический подход, обобщенный на случай многоуровневой системы [20]. В рамках этого подхода временная эволюция системы описывается системой дифференциальных уравнений [2; 7; 8; 12] для функций распределения плотности вероятности:

^ = L p w     sPS 2

- 8 k ne^s ( p s 2 - pC S ’),

n

• ( n )

— = i_{c s}i w     ^es

( n ) eS ^-

k n ^{( p}Cs ^{) - p}S 2 )

-

CR ( n )

⁸ k nm ^{( p}es m

• ^{( m} )        ^{1      ( n + 1)}

  ^{- p} s 1 ) ⁺   ( n + 1) ^pes

v

-

1        ( n )

( n + 1) ^pes ,

v

( m )

¹¹¹ S 1

W f

ˆ

( m )

L S ¹ S 1

- 8 k em ( p Sm ) - p e s ’) + m

____¹____ „( m + 1)

( m + 1) ^pS 1 v

-

1      ( m )

( m ) ρ S 1 ,

v

где      I S₂ (Q , t ) - функция распределения во втором возбужденном состоянии;

z S 1( m ) ( Q , t ) - на m -м подуровне первого возбужденного состояния;

z CS ⁽ n ) ( Q , t ) - на n -м подуровне состояния с разделенными зарядами;

Q – вектор с компонентами Q ₁, Q ₂, ... , Q_N ;

L ˆ , L ˆ и L ^ˆ _{S 1} – операторы Смолуховского, описывающие диффузию по термам U_CS , U_{S 2} и U_{S 1} соответственно.

N 2

Lо-8 (1 + й ^* № ^т), i-1           »Qi

N 2

Lsi - Ls2-8 -(1+ (Qi" 2E,) — + QЛ),

S1        S2                             i rii i-i 1 i                        »Qi где aQ^p - 2EikBT - дисперсия равновесного распределения по i-й координате;

k_B – постоянная Больцмана;

T – температура.

Здесь предположено, что инерционная компонента релаксации среды может быть заменена дебаевской. Обоснование такой замены дано в работе [3].

Скорости переходов k_n ^{( CS )} = k_n ^{( CS )} ( Q ) и k_nm ^{( CR )} = k_nm ^{( CR )} ( Q ) – между термами U_{S 2} и U_CS ⁽ⁿ⁾ , а также U _CS ^{( n )} и U_{S 1} ^{( m )} определяются выражениями (4) и (5), соответственно [2; 7]:

_?г ДЛ 2                                              nⁿр" S

CS                n                 (n)        2      2

kn (Q)      ^   b(US 2   U CS ), Vn    VCSFn, Fn n!   , z>t ту2                                                                            min(n,m)z i\n- rz Г^\п + m- 2r

E rv

, S 4- V , h o

Z,^{( CR )}(П\ — ² V nm ?.( ^m ) тт(ⁿ )\   TZ²        Г p       ^S _T1l,„₁ir        ⁽" 1)   ⁽' ^S )

knm (Q)---E(US 1 " UCS ), Vnm - VCRFnm , Fnm - e n !m ![ 8               h                                                           r=0 r!(n - r)!(m - r)!

где V_CS и V CR - электронные матричные элементы переходов S ₂ to CS и CS to S 1 ;

F_nm – фактор Франка-Кондона;

S – фактор Хуанга-Риса;

E_rv – энергия реорганизации эффективной ВЧ колебательной моды.

Параметры S и E_rv предполагаются одинаковыми для процессов разделения и рекомбинации зарядов [12].

Здесь предполагается одноквантовый механизм релаксации высокочастотной моды, в котором рассматриваются только переходы между соседними колебательными состояниями n to n - 1, протекающие с константой скорости 1/ i v ^{( n} ) . Зависимость времени релаксации от номера колебательного состояния имеет вид i v ^{( n} ) = i v W/ n [12].

Для формулировки начальных условий учтем, что возбуждение |S0р to IS2р не сопровождается значительным перераспределением зарядов. Это означает, что равновесное состояние полярной среды непосредственно после фотовозбуждения является хорошим приближением. Более того, поскольку длина волны возбуждающего импульса, используемого в экспериментах [4], близка к красной границе полосы поглощения |S0р to IS2р, то естественно считать, что высокочастотная колебательная мода после перехода оказывается в основном состоянии. С учетом этого началь- ные условия имеют вид:

i S 2 ( Q , t = 0) - Y

i

1         ¹ Qi ²   “

,             exp к-      , '„. i,

V24 Q)   ^к 2 й О ь

( n )                            ( m )

¹ CS ^{( Q} , t ^O) 0, ¹ S 1 ^{( Q} , t ^O) 0,

Система дифференциальных уравнений (1)–(3) с начальными условиями (6), (7) решалась численно с использованием ранее разработанных методов броуновского моделирования [6].

2.    Обсуждение результатов моделированияВлияние энергии реорганизации среды на выход продуктов

В этом разделе представлены результаты численного моделирования динамики разделения зарядов из второго возбужденного состояния S ₂ и последующей рекомбинации в состояние S ₁ в рамках рассмотренной модели. Расчеты проводились при комнатной температуре: k_BT = 0,025 эВ. Поскольку разница энергий между состояниями S ₂ и S ₁ во всех производных Zn-порфиринов практически неизменна, то она принималась фиксированной и равной „ G 12 = -0,7 эВ [18]. Значения электронных матричных элементов для рекомбинации и ионизации V_CR = V_CS = 0,02 эВ. Значение свободной энергии разделения зарядов „ G CS = -1,025 эВ, энергия реорганизации и частота эффективной внутримолекулярной колебательной моды E rv = 0,4 эВ и a v =0,1 эВ, соответственно, время колебательной релаксации i _v ⁽¹⁾ = 0,1 пс.

На рисунке 2 представлены результаты численного моделирования кинетики CS и CR в растворе ацетонитрила ( ACN ) при различных значениях энергии реорганизации среды E_rm . Функция релаксации растворителя X ( t ), соответствующая ACN , включает две моды с равными весами x 1 = x 2 = 0,5 и временами релаксации i 1 = 0,19 пс и i ₂ = 0,5 пс [16].

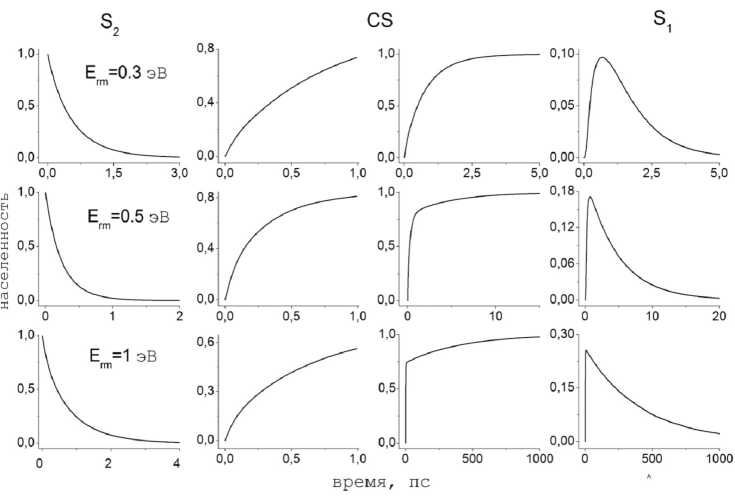
Рис. 2. Кинетика населенностей второго (левый столбец), первого (правый столбец) возбужденных состояний и состояния с переносом заряда (второй и третий столбцы). Использованы параметры, соответствующие ацетонитрилу. Значения E_rm одинаковые в строках и приведены в первой колонке

Анализ результатов, приведенных на рисунке 2, выявил следующие особенности: (I) заселение первого возбужденного состояния происходит в горячем режиме, поскольку терм состояния S ₁ во всех случаях лежит выше терма CS ; (II) распад состояния S ₂ быстрее протекает при E_rm = 0,5 эВ по сравнению с остальными случаями; (III) значение максимальной населенности состояния S ₁ увеличивается с ростом E_rm .

Эти особенности имеют простой физический смысл. Следует сказать, что горячая рекомбинация зарядов является единственным каналом заселения первого возбужденного состояния S1. Вторая является следствием того, что при Erm = 0,5 эВ наиболее мощный сток проходит через минимум терма S2, где в соответствии с начальным условием (4) наблюдается наибольшая населенность второго возбужденного состояния. Третья закономерность обусловлена тем, что наклон терма CS в точке его пересечения с термом S 1 равен Erm+ „ GCS. Скорость волнового пакета в окрестности этой точки пропорциональна наклону терма, который растет с ростом Erm и вероятность нетермической CR уменьшается.

Влияние динамических свойств растворителя на выход продуктов

Для демонстрации влияния функции релаксации растворителя на временную динамику населенностей состояний S ₂, S ₁ и CS было выполнено численное моделирование при использовании динамических параметров, соответствующих раствору тетрагидрофурана ( THF ) [10]: x ₁ = 0,443; x 2 = 0,557; i 1 = 0,226 пс и i ₂ = 1,520 пс. Все остальные модельные параметры такие же, как на рисунке 2. Результаты моделирования представлены на рисунке 3.

Детальное сравнение результатов численного моделирования, представленных на рисунках 2 и 3 для растворителей ACN и THF, соответственно, позволяет выявить следующие закономерности перехода к более медленному растворителю: (I) во всех случаях наблюдается увеличение максимальной населенности состояния S ₁; (II) наблюдается небольшое замедление распада состояния S ₂.

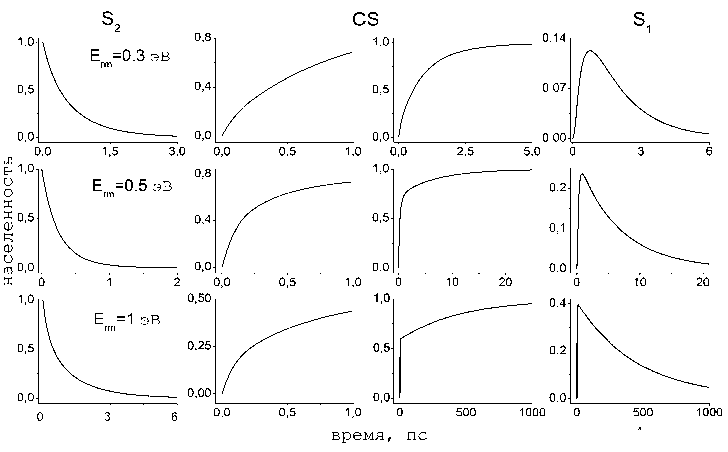
Рис. 3. Кинетика населенностей второго (левый столбец), первого (правый столбец) возбужденных состояний и состояния с переносом заряда (второй и третий столбцы) в растворителе с динамическими параметрами THF . Значения E_rm одинаковые в строках и приведены в первой колонке

Фитинг кинетики населенности состояния CS

В этом пункте выполнен полуколичественный фитинг кинетики населенности состояния CS , которая была получена в работе [17] для Zn(II)-порфирина, ковалентно связанного с нафталини-мидом в растворе диметилформамида ( DMF ) (см. рис. 4). Частота и время релаксации внутримолекулярной высокочастотной колебательной моды фиксированы и полагались равными &  = 0,1 эВ, i v ⁽¹⁾ = 0,05 пс. Наилучший фитинг, изображенный сплошной линией на рисунке 3, был получен при следующих модельных параметрах: E_rm = 0,80 эВ; E_rv = 0,60 эВ; V_CS = 0,10 эВ; V_CR = 0,05 эВ .

Модель, рассмотренная в этой работе, не включает в себя переход в основное состояние S ₀. CR в состоянии S ₀ протекает в термическом режиме и является достаточно медленной, следовательно, распад состояния CS в состояние S ₀ является экспоненциальным. Такой распад с константой скорости, k ₀, изменяет кинетику населенности состояния CS P _CS( t ) следующим образом:

P CS ( t ) = e "

k_ot t kt t В ^dPCS ⁽ t ^В ?

dt В

где P CS ( t ) является населенностью состояния CS с учетом распада в S 0 .

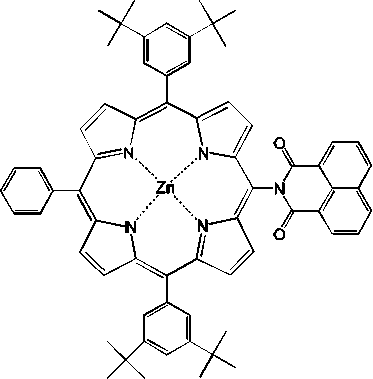
Рис. 4. Схема химической структуры диады, состоящей из Zn(II)-порфирина и нафталинимида

Рассчитанная кинетика населенности состояния CS , учитывающая переходы в состояние S ₀ (пунктирная линия), воспроизводит все особенности кинетики, наблюдаемой в эксперименте [17]: (I) два максимума на коротких временах (сто фс) и больших временах (несколько десятков пс); (II) величины обоих максимумов; (III) глубину провала между максимумами.

Из рисунка 5 видно, что переход к растворителю с одним временем релаксации не сильно изменил поведение кривой населенности состояния CS .

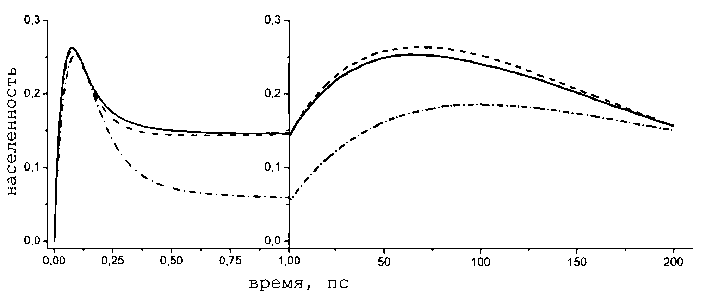
Рис. 5. Кинетики населенности состояния CS для Zn(II)-порфирина, ковалентно связанного с нафталинимидом в DMF . На левой части рисунка представлены данные до одной пикосекунды, а в правой части приведены данные для 1–200 пс. Сплошная линия является результатом моделирования при следующих динамических параметрах, соответствующих DMF [18]: x 1 =0,508; x 2 = 0,443; x 3 = 0,039;i 1 = 0,217пс;i₂ = 1,70 пс;i₃ = 29,1 пс. Пунктирная линия получена для растворителя с одним временем релаксации 1 1 = 0,5 пс. Штрихпунктирная линия соответствует более медленному растворителю с x ₁ = 0,5; x ₂ = 0,5;

1 1 = 0,5 пс; i₂ = 5 пс. Константа скорости рекомбинации S ₀ во всех случаях равна к ₀ = 0,015 пс

Использование более медленного растворителя с двумя временами релаксации практически не влияет на высоту первого максимума, но приводит к значительному уменьшению величины второго максимума.