Моделирование коэффициента преломления в линейном и нелинейном режимах для наноструктурного ситалла

Механическое нагружение, как известно, приводит к смещению потенциала межатомного взаимодействия [1], что вызывает изменение макроскопических свойств твердого тела в сравнении с его ненагруженным состоянием [2-3]. Данный эффект связан с различием в колебательной динамике ансамбля нелинейных осцилляторов, которые выступают элементами этой динамической системы и являются физической моделью твердого тела. В этой связи представляется интересным провести анализ поведения отдельного возбужденного осциллятора, нагруженного действием внешней силы. Подобного рода исследования, направленные на изучение динамики перераспределения кинетической и потенциальной энергии осциллятора, нагруженного постоянной внешней силой, представлены в [4-5]. В настоящей работе проводится исследование движения нагруженного нелинейного осциллятора под влиянием некоторого дополнительного периодического воздействия. А именно – моделируется эффект переизлучения поля оптическим электроном, движение которого искажено из-за внутреннего механического напряжения в веществе, внешнего светового поля для случая линейного и кубично нелинейного режимов мощностей. Это в свою очередь позволит получить коэффициенты, характеризующие макроскопические оптические свойства напряженного твердого тела - коэффициенты затухания и преломления. Согласование результатов приближенно-аналитического, численно-компьютерного решений и эксперимента приводят к заключению о правильности проведённых расчетов.

Модель нагруженного осциллятора

Нагруженный осциллятор является моделью оптических (переизлучающих) электронов, находящихся в составе атомов или молекул, расположенных по границам зерен кристаллита. Если рассматривается кристаллит в традиционно ква-зиравновесном состоянии, то погранично-зеренное искажение кристаллической решетки является небольшим [1], объем границ мал в сравнении с объемом зерен [3], и действие нагруженного осциллятора является достаточно малым в общей реакции вещества. Иначе обстоит дело для объемных нанокристаллических материалов (НКМ), которые являются существенно неравновесными веществами ввиду максимального объема: в процессе механической обработки кристаллита, применяемой для получения нанокристаллического материала, например, интенсивной пластической деформации (ИПД) [3], появляются зародыши (домены) с более мелким размером зерна по отношению к изначальному (или крупнозернистому) состоянию. С повышением степени деформации объем этих доменов увеличивается, постепенно захватывая все вещество. При этом даже еще в неравномерном по размеру зерна веществе вновь появляются домены с еще меньшим размером зерна и т.д. до стадии так называемой «наибольшей» деформации, когда уже не происходит зарождение таких доменов. Вещество становится однородным с приблизительно одинаковым размером зерна. Дальнейшее повышение деформации приводит к разрушению образца материала до состояния пылевидной структуры [6].) напряженных межзеренных границ [3]. Последние в результате механической обработки существенно уширены, а зерна – измельчены. В этом случае реакция напряженного осциллятора на внешнее поле (излучение) становится заметной и вполне определяет оптические макроскопические свойства НКМ.

Факт отличия оптических макроскопических свойств механически напряженного материала подтверждается результатами исследований, представленных в [7-11]. Тем не менее, невзирая на значительную актуальность прогнозирования свойств НКМ, в том числе в зависимости от методики их получения, в литературе практически не представлены аналитические подходы и модели, направленные на получение оптических макроскопических свойств НКМ. Последнее особенно значимо в связи с бытующим мнением о нецелесообразности применения НКМ при построении волоконно-оптических устройств и систем из-за их меньшей прозрачности (в сравнении с крупнозернистым состоянием вещества), что обусловлено раздроблением кристаллита при ИПД. Но проведённые исследования [10-13] подтверждают возможность применения прозрачных НКМ при построении перспективных устройств волоконной оптики, в результате чего является актуальной задача аналитического моделирования указанных свойств.

Целесообразность прогнозирования оптических макроскопических свойств НКМ на основе модели гармонического осциллятора объясняется наличием изменений спектра поглощения на-нокристаллических кварца и ситалла в ближней инфракрасной области (ситалл – стекло литиевой группы Li2O-Al2O3-SiO2 [14], по многим оптическим параметрам является близким к кварцевому стеклу SiO2, широко применяемому в волоконнооптической технике [10]). Это обстоятельство, согласно [3], объясняется электронной поляризо-ванностью, связанной с деформацией электронных орбит, и подтверждается электроннограммами. Видимым признаком являются существенно уширенные межзеренные границы. Авторы [7], наблюдавшие изменение спектра поглощения напряженного кристалла (NH4)2SO4, также связы- вают данный эффект с электронной поляризован-ностью.

Перечисленные выше НКМ проявляют новые оптические свойства также и в микроволновом диапазоне, что связано с ориентационной зеренной поляризованностью для измельченных зерен. Но этот случай является предметом отдельного моделирования и в настоящей работе не рассматривается.

Влияние напряженной уширенной границы на движение оптического электрона, находящегося в зернограничной области, может быть смоделировано при помощи нагруженного осциллятора [5], движущегося под действием неизменной вынуждающей силы. Если осциллятор смещен из состояния изначального (присущего веществу в изначальном крупнозернистом состоянии) равновесия ( x = 0) в новое состояние равновесия с координатой x ₀ (см. рис. 1), вокруг которого может совершать колебательное движение с относительной координатой y, причем y = x – x ₀, то уравнение движения для него будет иметь вид: my = U о - kx или, что то же самое: mx + kx = U 0 , где U o ^- сила, действующая со стороны напряженной границы.

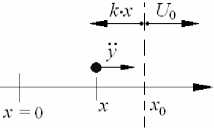
Рис. 1. Движение осциллятора, нагруженного действием напряженной границы

Еслиположить,что U –потенциальнаяэнергия, введенная в вещество в результате ИПД-обработ-ки, то U 0 может быть найдено как U 0 = grad ( U ) , причем значение U измеримо для элементов объема (для хрупких материалов такой элемент объема приблизительно равен 2 мкм³) НКМ методом мессбауэрографии [3], то есть составима карта потенциала деформации. В связи с тем, что рассматривается НКМ с высокой степенью деформации, то есть существенно однородное по объему вещество, можно для расчетов принять одномерный случай и положить U 0 =5 U/ d x . Для обеспечения возможности аналитического моделирования можно также принять U 0 = const ( x , t ) , где t – текущее время.

В случае, когда вещество находится под влиянием внешнего излучения, то на осциллятор, кроме деформационной силы, действует еще и сила со стороны этого излучения, характеризуемая напряженностью электрического поля E(t) свето- вой волны. Уравнение движения при этом будет иметь вид:

x + Ю02x = S0 • exp(jtot) + K0,        (1)

e где S0 = — E0, e и m - заряд и масса осциллято-m ра, E0 – амплитуда напряженности электрического поля внешней световой волны; ω0 и ω – собственная частота осциллятора и частота внешнего поля; K0 = U0 m ; j – мнимая единица. Очевидно, что установившееся движение осциллятора, описываемого на основе (1), будет также происходить с частотой ω, то есть, хотя движение электрона является искаженным из-за константы K0, он не будет излучать каких-либо волн, отличных от падающей.

Нелинейный нагруженный осциллятор

Иная картина складывается для нелинейного диапазона мощностей, когда движение описывается кубически нелинейным осциллятором Дуффинга [15]: X + ® 02 x + M 0 x ³ = S 0 • exp ( j m t ) , где M ₀ – коэффициент кубичной нелинейности. В [15] показано, что установившееся решение (общее решение не представляет интереса с точки зрения исследования процесса переизлучения) такого уравнения имеет вид x = A 1 • exp ( j ® t ) + A 3 • exp ( 3 j ® t ) . Оптическая интерпретация для решения x ( t ), представленная в [16], базируется на следующем соотношении для макроскопической поляризованности вещества: P = N e x [18], где N – концентрация оптических электронов.

В [16] показано также, что A ₁ представима в виде двух слагаемых: A ₁ = A ₁₀ + A ₁₁( E ₀²), определяющих линейный режим переизлучения и са-мовоздействие световой волны. Очевидно также, что слагаемое A ₃ характеризует генерацию третьей гармоники (реально для получения гармоник входного излучения, как известно, требуется наличие волнового синхронизма [17]. Здесь же представлена модель явления.) частоты ω в нелинейном диапазоне мощностей. Если представить x в виде x = P/N ■ e , то в рассматриваемой задаче уравнение осциллятора есть

Р+ to02 Р+M • Р3 = S • exp( jtot)+K, (2)

где M = M 0 /(Ne ) ² ; S = Ne ² E 0 /m ; K = Ne .

m

∂ U

∂ x

Из-за наличия постоянной составляющей установившееся решение (2) следует искать в виде

P = B • expjtot)+B2 • exp2jtot)+B3 • exp3jtot)+L. (3)

Применить метод разбиения на порядки малости по аналогии с [15] в исследуемой задаче не представляется возможным ввиду того, что слагаемое K не может быть адекватно отнесено к нулевому, либо первому порядку малости. Правильно было бы предположить, что деформационная составляющая имеет отношение к обоим порядкам малости. Поэтому для получения приближенно-аналитического решения соотношение (3) подставлялось в (2), после чего были собраны слагаемые с одинаковыми степенями экспоненты и приравнены соответствующие левые и правые части уравнения. Расчеты проведены при допустимости пренебрежения членами со степенями 4 jωt и выше. Последнее объясняется тем, что высшие гармоники практически никогда не наблюдаются в реальных физических экспериментах [17]. В результате указанных действий получена система алгебраических уравнений:

'В( ( to ₀ 2 -to² ) + 3L²MB 2 = S ;

B2(to02 -4to2) + 3L2M(в2 + LB2) = 0;        (4)

B3 (to02 - 9to2) + M(b3 + 3L2B3 + 6B1B2L) = 0;

ML + ®02 L = K.

Разрешение (4) относительно искомых коэффициентов проведено следующим образом. Параметры неполного кубического уравнения L + ^o_ l _ ^K = о таковы, что последнее имеет

MM

один действительный корень [19]: L1 = 3/2M + Qj +

+

K ²    ⎛ ω ² ⎞

^K + ⎜ ^{ω 0} ⎟ и два комплексно- 4M ^{2 ⎜} 3M ^⎟

сопряженных корня:

^L 2,3 ⁼

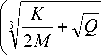
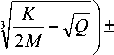
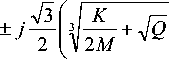
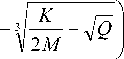
Обратим внимание на то, что L, согласно (3), являетсяпостояннойсоставляющейполяризован-ности вещества. Поэтому мнимая часть говорит о наличии потерь излучения, что с физической точки зрения весьма правдоподобно. Действительно, напряженное состояние, свойственное НКМ, со временем расслабляется, дефекты аннигилируют [3]. Наличие таких внешних факторов, как нагрев или облучение, может несколько ускорить данный процесс, но в данном случае не окажет кардинального влияния. Действительно, мнимая часть в соотношении для L2,3 является чрезвычайно малой. Если вынести из под знаков радикалов в мнимой части для L2 3 множитель К/2M, то Q после подстановки значащих коэффициентов (коэффициент М оценен приближенно из-за отсутствия точного значения входящего в его состав М0: приближенно в системе СИ для кристаллических тел М0 ® 10-10 [20]) в системе СИ будет примерно равен Q' ® 1 + 10-60, то есть Q' ~ 1. Это гово-

диэлектрической проницаемости вакуума, К -коэффициент диэлектрической восприимчивости вещества (в общем случае представляет собой

рит о том, что слагаемые, составляющие мнимую часть L 2 3 примерно сокращаются, следовательно, ею можно пренебречь. Тем не менее, с физической точки зрения следует выбирать именно комплексно-сопряженные корни, а действительный корень считать лишним. Если подобно описанному выше случаю в действительной части для

тензор, здесь допустимо рассматривать одномерный случай из-за однородности НКМ, возникающей под действием перемешивания при ИПД).

Параметр К определяет как линейные, так и нелинейные оптические свойства и для тра-

диционно используемых в оптике материалов го представим в виде К = ^(0) + ^7^(i) (E(t)), где

К ⁽⁰⁾ - коэффициент линейной восприимчивости,

L 2 3 откинуть малую часть, тем самым упростив соотношение, то получим: L 23 = L ^ —0,53/ K/M • Далее из первых двух уравнений системы (4)

не зависящий от энергетики входного излучения, K ⁽ⁱ⁾ - коэффициенты нелинейной восприимчивости. В решаемой задаче, как оказалось, коэффициент В также может быть представлен в виде

получаем, выразив В 2 в обоих случаях и приравняв их, квадратное уравнение относительно В1:

двух характерных слагаемых – не зависящего и зависящего от E ( t ). С учетом сказанного для

S — B ( го о — го ² )

3L ² M

^^^^^^в

3L ² MB 1 _____. Принимаем

( ® ₀ ² - 4 ® ² ) + 3L 3 M

во внимание оба корня ( B1 ) ₁₂ , далее после подстановки в первое из уравнений (4) получаем ( B 2 ) ₁₂ , и, после подстановки соответствующих

P = £0N(0)Eo exp(jtot) + £0N(1)Eo exp(jrot) +   (5)

+ s ₀ K ⁽²⁾ E ₀ exp ( 2 j ro t ) + e ₀ K ⁽³⁾ E ₀ exp ( 3 j ro t ) + P ₀ •

имеем:

корней в третье уравнение системы (4), получа- „          3M ( в, ³ + 6 B.B₇l )

ем соотношение для В .: в, = - у——^—— ^{1 2} ’

3        (ю02 - 9ы2) + 3L2M и корни (B3 )1,2. Чтобы откинуть лишние корни

_ℵ (0) ₌ 14e ²

17mε ₀

N

⋅

-

-

N ³ e ³ U ₀ ² ω ₀ ²

^^^^^^в

M 02 ⁽ ™ 02

-

4го ² )

^(D =^(D ( E ) =

находим значения их модулей и обеспечиваем выполнение условия: I B i I > I B 2 1 > I B 3 1, характерного для физического процесса, связанно-

3 го_п ²Е„ ² e ⁴ N

7(^ 27^х

X

го с параметрической генерацией гармоник [1 1; 17]. Данное соотношение характерно для всех без исключения кристаллов, традиционно применяемых для параметрической генерации. Если бы НКМ не было свойственно указанное соотношение, то нелинейный режим мощностей характеризовался бы, прежде всего, генерацией кратных го гармоник, а уже потом - самовоздействием. Экспериментальное изучение нелинейного влия-

^M 0 ^eNe 0 , ^cU o^/2_Y + x

^ ( ®0 - 4 ®² ) M 0 em

×⎜

ℵ ⁽

3 Ne ^⎜

9 M ₀ ³ c

E ₀

⎝

⋅

²⁷® o ( eU ₀/^,ms ₀ ® 02 + E ₀

- 1 e ² N ² ε 0 M 0 ⎟^⎞ K^2- ® ² ! ,

eN

ω ₀ -ω ²

(2) ₌ ¹

M 0 ε 0

15M ₀ ²

2 me ² N ² ( ® ₀ ²

-

4®2! 27s_t ⎝⎝

E 0

₂ ⋅                                   ₂

■ «о \eU_al^!т13^)₀ + E ₀ )

+

₊ e ² N ² ε ₀ M ₀

ния излучения на нанокристаллические кварц и ситалл [10-11] показало обратное: сначала появляется самовоздействие, выражающееся в виде нелинейного изменения показателя преломления, а только затем при существенном повышении мощности входного излучения (более, чем в 70 раз) начинает наблюдаться вторая гармоника, а затем и третья.

Подставим в полученные для В - В ₃ и L выражения физически значащие коэффициенты (см. пояснение к (2)) и представим (3) в виде, традиционно используемом в нелинейной оптике: P = s ₀ ^ E ( t ) [17; 20-21]. Здесь S o - коэффициент

2 ω ₀

-

ω ²

_⎟⎟_{E 0}2 ₊

_N 2 _e 2 _U

^M 0²

2/3   4 ⎞

0 ^ω 0     ⎟

2 ⎟

;

⎠

х ⁽³⁾ =

M ₀ ε ₀ ω ₀

26 meN ² ( ® ₀2 - 4 ® ² '( а >₀2

X

- 9 ® ² )

X

V

⎛

11M 0² E 0 _⎟⎞

17ε 0 ω 0^{2 ⎟}⎠

р. =

1 0

^^^^^в

e ² N ² ε ₀ ω ₀ ² M ₀ ²

+   /--------v;—X

₊    N ² e ³ U 0^5/3 ω 0⁴ _⎟⎟^⎞

M ₀ ² ms ₀ ( m ₀2 - 9m ² ) 2

2 (eN )32 J _U^ •

mM ₀

;

Анализ (6) показывает, что линейная составляющая диэлектрической восприимчивости К ⁽⁰⁾ весьма слабо зависит от степени механической деформации, характеризуемой параметром U ₀. Если положить U_o = 0, то <о> _ ¹⁴ e , N , ⁰           ^   = ^

17 m е ₀ ( го ₀ -го ) что приблизительно соответствует формуле Селмейера [17; 21], в которой все N оптических электронов имеют резонансную частоту го о . Отсюда следует вывод о том, что при переходе к напряжённому состоянию вещества его линейный показатель преломления меняется незначительно. Данный факт находит экспериментальное подтверждение в [11], где установлено, что показатель преломления наноструктурных ситалла и кварца для интенсивностей излучения порядка 1-10 ⁵ Вт/см ² отличается не более, чем на 5% от данного параметра для крупнозернистых материалов (результат получен для образцов НКМ, обладающих различными степенями деформации, отличающимися от наибольшей для данных материалов не более, чем на 10%). Известно [21], что вдали от резонансов поглощения линейный показатель преломления n ₀ связан с К ⁽⁰⁾ как n ₀ ² = К ⁽⁰⁾ + 1. Иначе обстоит дело с нелинейной составляющей диэлектрической восприимчивости. Для НКМ становится характерной вторая переизлучаемая гармоника, не свойственная изначальным образцам керровского типа [20], для которых переизлучение может происходить либо на частоте входного излучения, либо на её третьей гармонике. Кроме этого даже слагаемое, ответственное за самовоздейс-твие световой волны, связанное с параметром К ⁽¹⁾ , начинает зависеть не только от частоты ® 0 , но и от ее второй гармоники. Следует отметить, что для соотношений (6) характерно К ⁽¹⁾ > К ⁽²⁾ и К ⁽¹⁾ > К ⁽³⁾ , а К ⁽²⁾ ® К ⁽³⁾ , тогда как для ненапряжённых материалов некерровского типа (для которых происходит переизлучение и на частоте второй гармоники при параметрической генерации) имеет место К ⁽¹⁾ > К ⁽²⁾ > К ⁽³⁾ . Это говорит о том, что для НКМ генерация второй гармоники проявляется слабо, что также подтверждается экспериментально [11]. Обратим внимание, что для генерации кратных гармоник со значительными по величине амплитудами требуется выполнение волнового синхронизма [17; 20]. В [11] установлен лишь факт их появления с интенсивностями, незначительно превышающими порог чувствительности спектроанализатора.

Для анализа правомерности отбрасывания слагаемых высших гармоник при решении уравнения (2) и малых слагаемых при решении системы (4), уравнение (2) было решено численно с применением программного пакета Synplify 7.3.4 вдали от резонансов го0 Ф го, го0 Ф 2го и го0 фЗго. При решении использовались следующие значения физически значимых параметров (предполагалось, что в количестве молей вещества, находящегося на пути просвечивающего ситалловый образец конического луча, в каждой молекуле находится по 9 оптических электронов): N =1,1.1025, e = 1,6.10-19 Кл, m = 9.10-31 кг, M0 =1.10-10 (м2с2)-1, U0,min = 1.10-16 кг.м/с2, U0,max = 1.10-14 кг.м/с2, шаг Δ U0 = 1.10-16 кг.м/с2, E0,min = 3.104 В/м, E0,max = 3.108 В/м, шаг Д E0 = 3.104 В/м, Го0 = 1,3.1015 рад/с, romin = 1.1015 рад/с, ω max =1,2.1015 рад/с, шаг Δω =1.1013 рад/с. В результате решения были получены графические зависимости (данные кривые проводились при обеспечении минимального среднеквадратического отклонения относительно точек, полученных при численном решении уравнения) коэффициентов В1*, В2* и В3* от U0, E0 и го в указанных диапазонах изменения.

Установлено, что среднеквадратическое отличие графической В ₁^*(ω)и аналитической В ₁(ω) кривых не превысило 3,5%; кривых В ₁^*(E₀)и В ₁( E ₀) – 3% ; В ^*( U ₀)и В ( U ₀)– 3,7%.Аналогично В ₂^*(ω)и В ₂(ω) – 13¹ ,4%; кри¹ вых В ₂^*( E ₀) и В ₂( E ₀) – 12%; В ₂^*( U ₀) и В ₂( U ₀) – 13,2%; В ₃^*(ω) и В ₃(ω) – 14,5%; кривых В ₃^*( E ₀) и В ₃( E ₀) – 12,7%; В ₃^*( U ₀) и В ₃( U ₀) – 15%. Отсюда можно сделать вывод о том, что аналитические соотношения, входящие в (6), адекватнее отражают эффекты линейного преломления и нелинейного самовоздействия, характерных для напряженных материалов, чем эффекты параметрической генерации.

Для применения соотношений (6) в задачах моделирования и прогнозирования оптических свойств НКМ необходимо учесть резонансные потери, пограничнозеренные эффекты [22], оказывающие влияние на движение осциллятора, и уточнить коэффициент M ₀, характеризующий нелинейную жесткость. Принятое при проведении расчетов значение для M ₀ является весьма приближенным и не может применяться для получения практических результатов. Поэтому для уточнения M ₀, характерного для наноструктурного ситалла, решено было выполнить наложение графика нелинейного изменения показателя преломления, полученного экспериментально [11], и такого же графика, построенного с использованием соотношений для К ⁽⁰⁾ и К ⁽¹⁾ , входящих в (6).

Известно [17-18; 21], что нелинейное изменение показателя преломления характеризуется следующей его зависимостью от интенсивности I: n(I) = n ₀ + +n ₂ 1, где в принятых обозначениях

E ²

^{I =} _2Z ^{0 ,} волновое сопротивление направляющей среды; n ₀ и n ₂ – линейный и керровский показатели преломления, связанные с коэффициентами диэлектрической восприимчивости (вдали от резонансов поглощения) [21]:

n ₀ = Тк^ГГ и n ₂

— Re К ⁽¹⁾ ] . (7) 8 n о

Так для принятого ранее в расчетах M ₀ был построен теоретический график n ( I )для Z = =185π Ом, пересчитанных E _0,min= 3^.10⁴ В/м, E _0,max = 3^.10⁸ В/м,ис-ходя из экспериментальных значений минимальной и максимальной интенсивности,участвующих в экспериментах [11],и U ₀ = 8,5^.10^-15 кг^.м/с²,полученного на основании мессбауэрографии нанокристаллических ситалловых образцов (см.рис.2).Уточнять значения U ₀ при построении теоретического графика n ( I ) в соответствии с параметрами каждого из образцов не имело смысла,так как отличие значений,получен-ных с учетом реальной точности мессбауэрографа, составляли менее 1%,а точность метода теоретического моделирования n – в пределах 3...4%.

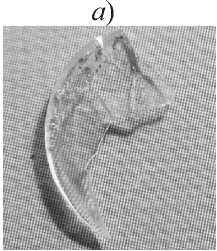
Рис. 2. Иллюстрация наиболее крупных фрагментов нанокристаллических ситалловых образцов, соответствующих различной степени деформации: а – относительная степень деформации υ составляет 88% от максимального значения (см. также данные рис. 3), U _0ср = 8,44175^.10^-15 ± 0,5^.10^-19 кг^.м/с²; б – υ составляет 90% и U _0,ср = 8,47228.10^-15 ± 0,5.10^-19 кг.м/ с²; в – υ составляет 97% и U = 8,49779.10^-15 ± 0,ср                        1

0,5.10-19 кг.м/с2

Оценки среднего параметра U0 ср,расположенно-го на линии просвечивания (линия или направление просвечивания для каждого из исследуемых образцов была определена ранее,что позволило при экспериментальном исследовании n обеспечить «захват» областей с наибольшим содержанием нанокристал- лических включений,что важно в связи с неоднородностью образцов по своей внутренней структуре и объясняется характером ИПД-обработки),дает ре-зультаты,указанные в подписи к рис.2.

Построенный график n ( I )существенно отличался от аналогичной зависимости,полученной экспериментально [11].Поэтому далее был выполнен итерационный пересчет параметра М ₀ с получением значения М ₀^*,обеспечивающего различие графиков n_теор ( I ) и n_эксп ( I )по максимуму среднеквадратического отклонения не более 3%.Полученное значение М ₀^* для наноструктурного ситалла составило: М ₀^*=2,47^.10^-9 (м 2 с 2 ) -1 .

Аналогичное исследование для наноструктурного кварцавыполнитьнепредставлялосьвозможнымвви-ду отсутствия полученной с достаточной точностью зависимости n _эксп(I).Кварцевые образцы оказались существенно более хрупкими и могли подвергаться ИПД-обработке лишь до незначительных степеней деформации (с ε не более 40...50%).С повышением ε образцы теряли прозрачность (см.рис.4).

в

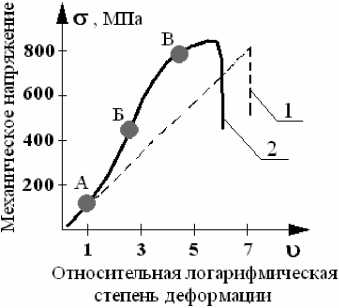
Рис.3.Иллюстрация электроннограмм и диаграмма де-формации: а – электроннограмма нанокристаллического ситалла с незначительной степенью деформации; б – со средней и в – со значительной степенью деформации; г – зависимость механического напряжения от степени деформации для исследуемых материалов:1 – кварцевое стекло; 2– ситалл

а)

б)

Рис. 4. Иллюстрация ситалловых ( а ) и кварцевого ( б ) образцов, подвергнутых ИПД-обработке: а – обработанный ситалловый образец справа

Учет влияния зернограничных эффектов

Получив значение М ₀^*, характерное для напряженного ситалла, можно уточнить математическую модель движения осциллятора. Уравнение (2) перепишем в виде:

P +y P +® 02 P + M • P ³ = S • exp ( j to t ) + K * ( p ) , (8) где γ – коэффициент,характеризующий спектральную ширину электронных резонансов и ответственный за резонансное поглощение в веществе; K ^* – параметр деформации, зависящий от состояния межзеренных границ. Согласно [22], если в зернограничной области имеет место напряжение, связанное с деформацией формы зерен (в [22] форма зерна описывается некоторой потенциальной поверхностью,наличие деформации характеризуется ненулевым параметром напряжения границы Ф.

Последний имеет размерность длины,которую можно трактовать как длину вектора смещения «свободной» границы под действием этого же потенциала напряжения),то сила U ₀, входящая в (1) и действующая на электроны (согласно [22], для НКМ,обла-дающих степенью деформации не меньшей 90% от наибольшей,каждый третий атом (или молекула) расположен в зернограничной области)в зернограничной области будет зависеть от смещения y. Если предположить,что в процессе облучения НКМ там не будут происходить фазовые переходы на границах зерен,их форма останется неизменной и не произойдет миграция границ,то для границ типа кручения из [2] следует: U ^ Л ( y + Ф ) 85 , где Л - параметр, характеризующий поверхностные свойства зерен кристаллита рассматриваемого материала независимо от размеров данных зерен,в данном случае обладающих границами типа кручения; Φ – параметр напряжения границы. Учитывая,что x = P Ne и то, что в состоянии равновесия осциллятора x ₀ поляри-зованность вещества равна нулю,получаем:

._ Ne

K =   ⋅

m

d U ( x ) = 8 _л Ne <  P

∂ x    5 m ⎝ Ne

у

V 5

Численное решение уравнения (8) с учетом (9) было проведено для следующих значений параметров (параметры, которые не вошли в перечень, соответствуют представленным выше): М ₀^* = 2,47.10^-9 (м²с²)^-1, E _0,min = 3.10⁴ В/м,

б)

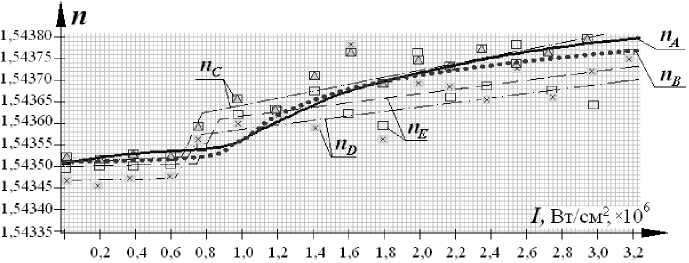
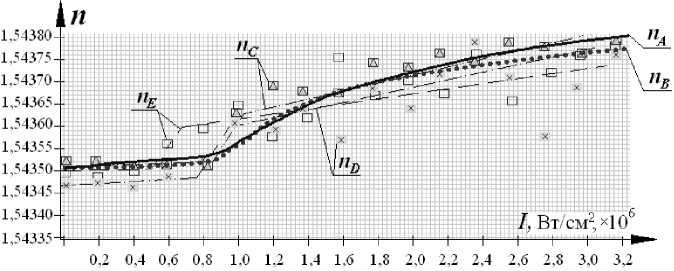
Рис. 5. Иллюстрация характера нелинейного изменения показателя преломления для наноструктурных ситал-ловых образцов: а – λ 1 = 1546 нм; б – λ 2 = 980 нм

E _0,max = 3.10⁸ В/м, шаг Δ E ₀ = 3.10⁴ В/м, ω₁ = 1,36^.10¹⁵ рад/с (соответствует λ ₁ = 1546 нм, первый случай), ω₂ = 1,91^.10¹⁵ рад/с (соответствует λ₂ = 980 нм, второй случай), γ = 1^.10^-8 с^-1, стекла литиевой и натриевой групп, согласно [23], характеризуются Л = 1,24-10 " ⁹ , для U 0 = 8,5^.10^-15 кг^.м/с² в соответствии с таблицами [24], отражающими свойства хрупких материалов, находим Ф = 5,3-10 ^-7 м.

Поаналогиисописаннымвышебылополучено значение коэффициента диэлектрической восприимчивости К ⁽¹⁾ , отражающего самовоздействие -как коэффициент при множителе exp ( jtot ) с учетом значения К ⁽⁰⁾ , вычисляемого в соответствии с (6). Действовало предположение, что линейные свойства материала мало зависят от внесенных в (8) поправок. Далее с учетом (7) производился пересчет нелинейного показателя преломления, связанного с E₀. На рис. 5 представлены графики n ( I ), полученные в результате: решения (2) с уточненным М ₀^* – n _A( I ); решения (8) – n _B( I ) и в результате экстраполяции экспериментально наблюдаемых значений – n _C( I ), n _D( I ) и n _E( I ) соответственно для образцов (см. рис. 2) а , б и в .

Согласно рис. 5, график n ( I ) имеет выраженный скачкообразный характер, не свойственный изначальному (крупнозернистому) ситаллу. Анализ результатов, представленных в [11], показывает, что с увеличением интенсивности n почти не меняется до некоторого критического значения I _cr, далее происходит его скачкообразный рост, а затем график переходит к линейному возрастанию показателя преломления, свойственного крупнозернистому ситаллу. В качестве отличия в третьей области можно рассматривать наклон прямой n ( I ), который несколько больше для наноструктурного ситалла, чем для крупнозернистого. Все это позволяет говорить о так называемом задержанном режиме нелинейного преломления. Анализируя соотношения (6) можно сказать, что задержанный режим связан с нарастанием E ₀ относительно U ₀, откуда очевидно, что положение скачка зависит от степени деформации. В [11] был сделан аналогичный вывод. Видно также, что характер n ( I ) зависит и от длины волны подводимого излучения. С увеличением энергетики излучения (1 1 > 1 ₂ ) разброс экспериментально наблюдаемых значений увеличивается, что может свидетельствовать о появлении зернограничных процессов в материале.

Меньшее расхождение теоретических кривых по сравнению с экспериментально полученными значениями можно объяснить наличием других определяющих свойства материала влияющих факторов, не учтенных в (8), а также влиянием внешних факторов в эксперименте.

Выводы

Проведено математическое моделирование коэффициента преломления в линейном и нелинейном режимах мощностей для наноструктурного ситалла. Аналитический метод основан на модели движения напряженного осциллятора, подвергающегося действию внешней световой волны. Показано, что нелинейный режим движения сопровождается самовоздействием, связанным с переизлучением частоты входного излучения, а также возможной генерацией второй и третьей гармоник указанной частоты. Наличие второй гармоники отличает нелинейный режим, свойственный напряженному материалу, от аналогичного для ненапряженного материала.

В результате сравнения приближенно-аналитического и численного решений уравнения движения установлено, что погрешность метода нахождения коэффициента преломления составляет порядка 3…4%. Благодаря сравнению результатов моделирования со значениями показателя преломления, полученными экспериментально, произведено уточнение математической модели – определен коэффициент нелинейной жёсткости для наноструктурного ситалла. Благодаря чему удалось получить численное решение уравнения, содержащего уточненную правую часть, учитывающую зернограничные свойства напряжённого материала. Проведено сопоставление полученных аналитическим путем зависимостей, определяющих изменение показателя преломления от интенсивности вводимого излучения. Установлено примерное соответствие характеру зависимости, полученной экспериментальным путем, содержащей три характерных участка – задержанный нелинейный режим, скачкообразный рост и пологий почти линейный рост показателя преломления в нелинейном режиме.