Моделирование колебаний уровня воды в дельте дона по прогнозам ветровой ситуации
Автор: Чикин А.Л., Кулыгин В.В., Чикина Л.Г.
Рубрика: Краткие сообщения
Статья в выпуске: 3 т.16, 2023 года.
Бесплатный доступ
Представлена математическая модель, состоящая из модели гидродинамики всего Азовского моря, включая Таганрогский залив, и модели движения воды в русле Дона. Данная модель позволяет рассчитывать колебания уровня воды в устьевой области Дона в зависимости от ветровой ситуации над акваторией Азовского моря и Таганрогского залива. Такой подход дает возможность заблаговременно предсказать изменение уровенной поверхности в основных рукавах реки Дон, а также в его основном русле. Гидродинамика Азовского моря описывается уравнениями мелкой воды, а движение воды в основных рукавах дельты Дона - уравнением Сен-Венана. Задача решается конечно-разностными методами. Программа написана на языке FORTRAN и реализуется на высокопроизводительных вычислительных системах в среде MPI с применением пакета Aztec. Для прогнозов ветровой ситуации использовались данные Норвежского метеорологического института. Прогнозируемая ветровая нагрузка над акваторией Азовского моря задавалась по точкам, соответствующим расположению береговых гидрометеорологических станций с последующей интерполяцией на всю акваторию. Рассмотрены две задачи прогнозирования колебаний уровня воды. Первая задача заключалась в расчете колебаний уровня в зависимости от прогноза ветровой ситуации с заблаговременностью три дня. Во второй задаче изучалась динамика изменения качества прогноза в фиксированном промежутке времени по мере приближения к его началу. Качество прогнозов определялось сравнением прогнозируемых и наблюденных значений уровня, полученных на гидропостах. Результат сравнения показал, что представленная модель достаточно адекватно описывает гидродинамику в дельтовой области Дона в зависимости от ветровой ситуации над акваторией Азовского моря.
Неустановившееся течение, вычислительный эксперимент, сгонно-нагонное явление, русловой поток, заблаговременный прогноз, дельта дона
Короткий адрес: https://sciup.org/147241748
IDR: 147241748 | УДК: 532.543.2 | DOI: 10.14529/mmp230307
Текст краткого сообщения Моделирование колебаний уровня воды в дельте дона по прогнозам ветровой ситуации
Считается, что устьевая область Дона расположена в границах от станицы Раз-дорской в основном русле Дона до Должанской косы в Таганрогском заливе [1, 2].
Уровень воды на нижнем участке р. Дон от Кочетовского гидроузла до устья подвержен различным по величине и периоду колебаниям, связанными как с основными фазами водного режима (как межень и половодье), так и обусловленным ветром, вызывающим сгоны и нагоны [3]. Сочетание стоковых колебаний уровня со сгоннонагонными колебаниями, возбуждаемыми на взморье, создает в устьевой области Дона весьма сложный и быстро меняющийся рельеф водной поверхности [4].
Чаще всего сгонно-нагонные явления наблюдаются весной и осенью. Для осеннего периода характерно влияние ветров восточного направления, которые вызывают сгон воды, что неблагоприятно влияет на судоходство. Так, в октябре 2015 и 2016 гг. наблюдался экстремально низкий уровень воды в Дону, вызванный продолжительными действиями восточных ветров, а также низким попуском воды на Цимлянском гидроузле. Это привело к тому, что суда были вынуждены простаивать в восточной части Таганрогского залива несколько дней, как это было 24.10.2016 [5]. Ветры западного направления вызывают нагон воды из Таганрогского залива. Экстремальные нагоны в дельте Дона в 2013 и 2014 гг. подробно описаны в работах [6, 7].
В этой связи актуальными задачами становятся не только качественный мониторинг, но и развитие методов прогнозирования и раннего предупреждения. Величина уровня воды в руслах рек зависит как от количества атмосферных осадков, высоты снежного покрова так и от ветровой ситуации в принимающем водоеме. При краткосрочном прогнозировании изменения уровенной поверхности русла реки используются различные методы: от основанных на графических зависимостях до математических моделей.
Для краткосрочного прогнозирования уровней воды в р. Амур разработана система методик, в основе которых лежит метод соответственных уровней, позволяющий упрощенно описывать движение и трансформацию волн паводков и половодий в русловой сети на основе данных гидрометрических наблюдений [8]. В работе [9] выполнено краткосрочное прогнозирование уровней воды у г. Барнаула по методу соответственных уровней. В основу метода положена графическая связь между уровнями воды в верхнем и нижнем створах.
В работе [10] представлен расчетно-модельный комплекс, предназначенный для выполнения диагностических и прогностических расчетов положения уровенной поверхности, скоростей течения и расходов воды в русле Дона. В основе комплекса лежит модель DELFT-3D, разработанная независимым нидерландским институтом прикладных исследований в сфере поверхностного и подземного стока.
В настоящей работе для расчета колебаний уровня воды в дельте Дона по прогнозам ветровой ситуации предлагается математическая модель, которая объединяет модель гидродинамики Азовского моря и модель движения воды в русле Дона. Обе эти модели были ранее разработаны в Южном научном центре РАН.
Целью настоящей работы является моделирование значений уровней воды в устьевой области Дона в зависимости от ветровой ситуации над Азовским морем, а также изучение влияния качества прогнозов ветров на результаты этого моделирования.
1. Материал и методы исследования
В качестве прогнозной ветровой ситуации использовался прогноз Норвежского метеорологического института []. Ветровая нагрузка над акваторией Азовского моря задавалась по 7 точкам, соответствующим расположению береговых гидрометеорологических станций Бердянск, Геническ, Ейск, Мариуполь, Приморско-Ахтарск, Таганрог и Темрюк, с последующей интерполяцией на всю акваторию. Шаг прогноза составляет 1 час с заблаговременностью почти трое суток.
После расчетов по прогнозной ветровой ситуации проводились расчеты уровня воды по уже наблюденным значениям ветра на метеорологических станциях. Периодичность измерения на метеостанциях – 8 раз в сутки с шагом 3 часа. В связи с трудностями получения регулярных наблюдений на станциях Бердянск, Геническ и Мариуполь в момент исследования их пришлось заменить данными с других метеостанций. Как показали расчеты, замена значений в Бердянске и Мариуполе значениями, измеренными на станции Должанская, а Геническ — значениями станции Джанкой, дают значительно лучшие результаты, чем при замене всех трех станций значениями станции Таганрог. Следует также отметить, что в наблюденных данных направление ветра указано по румбам (т.е. точность около 10 ° ), в отличие от прогнозов ветра, где направление ветра указано с точностью до 0,1 ° .
Расчетные и наблюденные значения уровня воды на гидропоту Донской, расположенному в дельте Дона на рукаве Старый Дон, снимались через каждый час. Наблюденные значения уровня воды брались с сайта Эмерсит [].
Погрешность расчета определялась по формуле с _ II a - a0 II " II ao II , где a – вектор, координатами которого являются расчетные значения, a0 – вектор, координатами которого являются соответствующие наблюденные значения, || a ||= al + a2 + ... + аП.
Представленная модель работает по следующему принципу. На каждом временном шаге сначала рассчитываются скорости течения и величина уровня воды в Азовском море по заданной ветровой ситуации. После этого по полученным значения уровня воды, которые соответствуют точкам устьев основных рукавов Дона, производится расчет гидродинамических параметров течения в рукавах Дона. Данный подход позволяет наблюдать за параметрами течения как в основных рукавах Дона, так и в Таганрогском заливе.
Движение воды в Азовском море (морская часть модели) описывается уравнениями мелкой воды:
|
∂u ∂t |
∂u ∂u + UgX + Vdy - Qv : |
∂ζ τ sx = - g aX + H |
τ bx H, |
|
∂v |
∂v ∂v |
∂ζ τ |
τ by |
|
— |
+ u-^—+ v^—+ Qu : |
= -Qtt- + ^y |
|
|
∂t |
∂x ∂y |
∂y H |
H , |
|
ас + д (Hu) + |
d ( Hv ) A ------- = o. |
||
|
∂t ∂x |
∂y |
Здесь u = u(x, y,t),v = v(x, y, t) - компоненты скорости; Q - коэффициент Кориолиса; Z = Z(x,y,t) — возмущение уровня воды; H = h + Z ; h = h(x, y) — глубина Азовского моря; τ sx , τ sy – проекции на оси OX и OY силы трения ветра о поверхность водоема; T bx , T by - проекции на оси OX и OY силы трения жидкости о дно; g = 9, 81 - значение ускорения свободного падения. Проекции сил трения зависят от скорости ветра W b = { W x ; W y } и течения W T = { u; v } и определяются так [11]:
T s = y | W b I W b ,т ь = в | W t I W t ,
|Wb I = VWx2 + W2, Wt I = Vu2 + v2, где γ – коэффициент трения ветра о свободную поверхность; β – коэффициент трения жидкости о дно. Приведенная система замыкается соответствующими граничными условиями. Вдоль твердой границы ставятся условия скольжения Vn = 0, dVT/дп = 0, где Vn и VT - нормальная и касательная составляющие вектора скорости соответственно. В точках, соответствующих устьям рек, задаются скорости втекания воды. В качестве начальных данных можно задавать какое-либо известное распределение скоростей (ранее полученное) или считать эти скорости нулевыми.
Для расчета русловой составляющей модели необходимо знать уровень воды в устьях рукавов Дона в Таганрогском заливе и задачу можно было ставить только для залива. Однако морская составляющая модели включает в себя Азовское море в целом. Это объясняется двумя причинами. Во-первых, гидродинамика Таганрогского залива полностью определяется гидродинамикой самого Азовского моря, а во-вторых, такой подход существенно облегчает решение задачи, так как отпадает необходимость ставить граничные условия на открытой границе Таганрогского залива.
Движение воды в основных рукавах дельты Дона описывается уравнениями Сен-Венана в предположении отсутствия распределенного бокового притока. Считается, что поперечное сечение русла имеет параболический профиль [12]:
' dz, 1 dQ = o
dt + B dx 0
∂Q ∂z ∂Q ∂v Q | Q |
+ gW — + a sv-— — — a s Q— g W ,
∂t ∂x ∂x ∂x K 2
где z – уровень воды; t – время; B – ширина русла; Q – расход воды; x – координата; W – площадь живого сечения; K – модуль расхода. Коэффициент α s учитывает неравномерное распределение скоростей по живому сечению потока, и для идеализированных русел рукавов с параболической формой поперечного сечения он обычно близок к единице. Модуль расхода K вычисляется по формуле K — W • CVR, здесь C – коэффициент Шези; R – гидравлический радиус. Коэффициент Шези вычисляется по формуле Маннинга C — R 6 /п, где п - шероховатость дна. Шероховатость дна оценивалась по фактическим наблюдениям, выполненным в ходе экспедиционных работ на НИС ≪ Профессор Панов ≫ в дельте Дона и на Нижнем Дону в 2020 – 2022 гг.
Предыдущую систему можно записать в характеристическом виде:
( gW^ + ■ + gw^ + Л,■ — ,_ A i at at Хх Хх gW^ + λ2 ∂t ∂t ∂x ∂x где asv ± J(asv)2 + 4c2 A1,2 — -----------^-----------, V— gW B. -αsQ∂∂xv - gW QK|Q2|, c — Граничные условия задаются следующим образом. В точке, соответствующей самой верхней точке основного русла, задается расход поступающей воды Q0 (0,t), в точках, соответствующих устьям рукавов, задаются уровни воды в Таганрогском заливе zk (Xk, t). В узлах ветвления на рукава Дона задаются условия равенства расходов притоков и оттоков ^2Q* — 0 (i - число рукавов, приходящих в узел ветвления). i Уровни водной поверхности в узлах ветвления равны между собой zi — z*. И морская, и русловая части модели решаются конечно-разностными методами. Программа написана на языке FORTRAN и реализуется на высокопроизводительных вычислительных системах в среде MPI. При конечно-разностной аппроксимации морской части модели получаются системы линейных алгебраических уравнений с блочными пятидиагональными матрицами, для решения которых используется пакет прикладных программ Aztec. При конечно-разностной аппроксимации русловой части модели полученная система линейных алгебраических уравнений также имеет преимущественно пятидиагональный вид, но она представляется как ленточная матрица общего вида. Решение этой системы линейных алгебраических уравнений проводится с помощью пакета LAPACK. Численная реализация представленных подмоделей подробно описана в работах [13, 14].
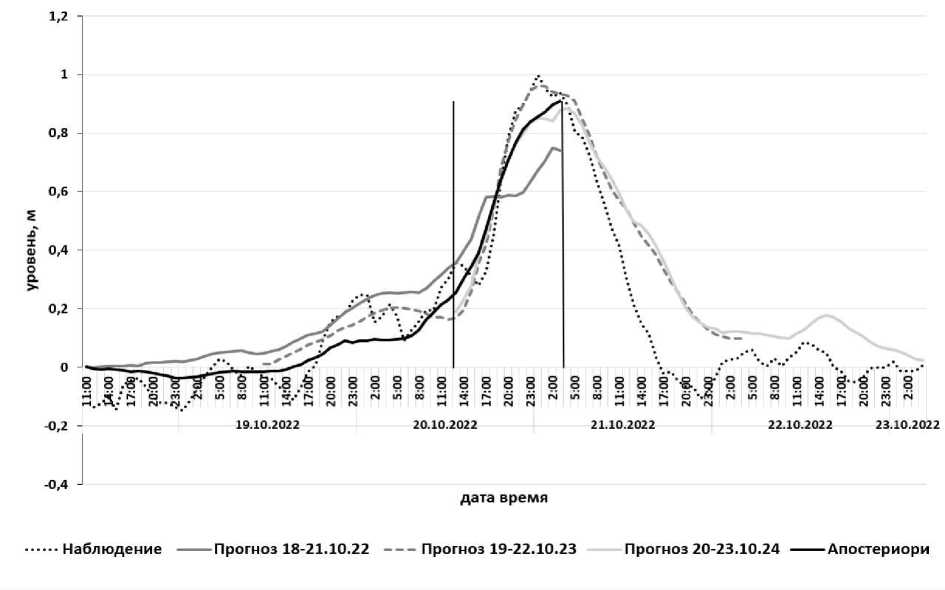
2. Результаты и обсуждения Были рассмотрены две задачи прогнозирования колебаний уровня воды. Первая задача заключалась в непосредственном прогнозе колебаний уровня в зависимости от ветровой ситуации. Для этого по прогнозу ветровой ситуации от 26.09.2022 был проведен расчет изменения уровня воды на станции Донской в период с 12:00 26.09.2022 по 3:00 29.09.2022. Затем было проведено сравнение с уже наблюденными значениями уровня воды в этот же период. На рис. 1 приведены графики расчетных и наблюденных колебаний уровня воды, полученные через каждый час на станции в Донском. Расчеты проводились как по прогнозному значению ветра, так и по наблюденной ветровой ситуации. Погрешность расчетных значений уровня воды, полученных по прогнозным значениям ветра, в сравнении с наблюдениями значениями составляет 56,6 %. Если проводить расчет по наблюденным значениям ветра (апостериори), то погрешность расчетных значений в сравнении с наблюденными значениями уровня воды составляет 19,2 %. Рис. 1. Колебания уровня воды в Донском в период с 12:00 26.09.2022 по 3:00 29.09.2022 Вторая задача заключалась в изучении динамики изменения качества прогноза уровня воды в фиксированном промежутке времени по мере приближения к его началу. Для этого были рассмотрены три прогнозируемых периода времени: с 10:00 18.10.2022 по 3:00 21.10.2022; с 10:00 19.10.2022 по 3:00 22.10.2022 и с 12:00 20.10.2022 по 3:00 23.10.2022, для каждого из которых был сделан прогноз ветровой ситуации с заблаговременностью трое суток. Общим для этих трех периодов является промежуток с 12:00 20.10.2022 г. по 3:00 21.10.2022 г., который совпадает с началом третьего периода, концом первого и целиком находится во втором периоде. Для этого промежутка и решалась задача определения качества прогнозов уровней воды, исходя из ветровой ситуации по прогнозам от 18.10.2022, 19.10.2022 и 20.10.2022. Динамика изменения качества прогнозов по мере приближения к выделенному промежутку времени представлена в таблице. Качество прогноза выражено в погрешности между расчетными и уже наблюденными значениями уровня воды. Там же приведена погрешность значений уровня воды, рассчитанных по наблюденной ветровой ситуации (апостериори). Все расчетные и наблюденные значения уровня воды снимались через 1 час после начала действия соответствующего ветра. Таблица Погрешности расчетных значений в промежуток с 13:00 20.10.2022 по 4:00 21.10.2022 для прогнозируемых ветровых ситуаций № Дата прогноза Погрешность 1 18.10.2022 10:00-21.10.2022 3:00 29,2 % 2 19.10.2022 10:00-22.10.2022 3:00 10,1 % 3 20.10.2022 12:00-23.10.2022 3:00 22,8 % (13,8 %) 4 Апостериори 12,0 % Рис. 2. Изменение уровня воды в Донском по прогнозным и наблюденным значениям ветровой нагрузки Лучший результат наблюдается для второго прогноза, хотя он ожидался для третьего. Возможно, это объясняется заданием нулевых начальных данных на начало каждого периода. Однако начало третьего периода совпадает с началом исследуемого временного промежутка (рис. 2), что может давать большую погрешность. Если в качестве начальных данных брать значения уровня из второго прогноза в соответствующий началу третьего периода момент времени, то погрешность существенно уменьшается до 13,8 %, однако остается больше погрешности для второго прогноза. Возможно, это объясняется тем, что наблюдения на станциях Бердянск, Геническ, Мариуполь не проводились, а заменялись измерениями на станциях Должанская и Джанкой. Кроме того, на результаты могло повлиять более грубое (с точностью до румба) задание величины наблюденного направления ветра при метеонаблюдениях. Выводы При расчете прогнозов уровня воды в дельте Дона принципиальное значение имеет качество заданной ветровой ситуации над акваторией Азовского моря, что вполне естественно. Ошибки в прогнозе ветровой ситуации приводят к существенным погрешностям расчета величины уровня воды. При отсутствии данных на одной или нескольких станциях важно правильно подобрать им замену (разница может быть существенной). Сравнение прогнозов ветра с наблюдениями показало, что лучшие прогнозные значения, по крайней мере для данных исследуемых периодов, определены для станции Ейск, и значительно худшие – для станции Таганрог. Видимо, этим объясняется тот факт, что при апостериорной оценке качества модели замена значений в Мариуполе и Бердянске значениями Должанской дает лучший результат, чем замена значениями в Таганроге. Сравнение расчетных и наблюденных значений уровня воды показало, что представленная модель адекватно описывает прогнозируемую гидродинамику в дельтовой области Дона при прогнозах ветровой ситуации над Азовским морем с заблаговременностью трое суток. Публикация подготовлена в рамках реализации ГЗ ЮНЦ РАН, номер проекта 122011900153-9.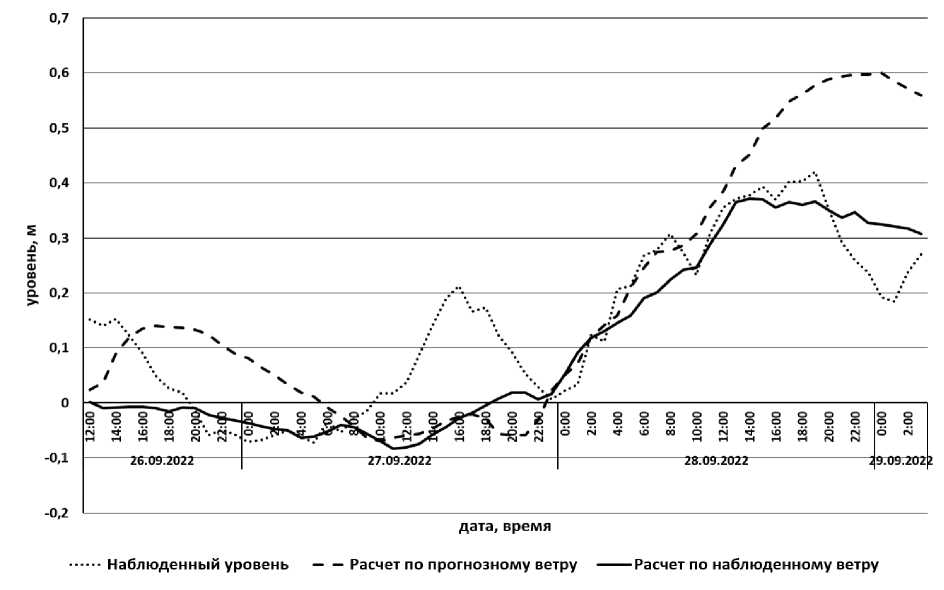
Список литературы Моделирование колебаний уровня воды в дельте дона по прогнозам ветровой ситуации
- Остроумова, Л.П. Исследование нагонных и сгонных явлений в морских устьях рек на примере устьевой области р. Дон / Л.П. Остроумова // Метеорология и гидрология. -2017. - Т. 12. - С. 69-82.
- Симов, В.Г. Гидрология устьев рек Азовского моря / В.Г. Симов. - М.: Гидрометеоиздат, 1989.
- Пономаренко, Е.П. Сгонно-нагонные явления в дельте реки Дон в 2007-2010 гг. и их прогнозирование / Е.П. Пономаренко, В.В. Сорокина, П.А. Бирюков // Вестник Южного научного центра РАН. - 2012. - Т. 8, № 1. - С. 28-37.
- Родионов, Н.А. Гидрология устьевой области Дона / Н.А. Родионов. - М: Гидрометеоиздат, 1958.
- Матишов, Г.Г. Мир каравайки и взморья глазами донских казаков / Г.Г. Матишов, А.И. Ермолаев. - Ростов-на-Дону: ЮНЦ РАН, 2016.
- Матишов, Г.Г. Экстремальное затопление дельты Дона весной 2013 г./ Г.Г. Матишов, С.В. Бердников // Известия Российской академии наук. Серия географическая. - 2015. -№ 1. - С. 111-118.
- Матишов, Г.Г. Экстремальное затопление дельты Дона весной 2013 г.: хронология, условия формирования и последствия / Г.Г. Матишов, А.Л. Чикин, С.В. Бердников, И.В. Шевердяев, А.В. Клещенков, Е.Э. Кириллова // Вестник Южного научного центра РАН. - 2014. - Т. 10, № 1. - С. 17-24.
- Борщ, С.В. Краткосрочное прогнозирование уровней воды на реке Амур / С.В. Борщ, Ю.А. Симонов, А.В. Христофоров, Н.М. Юмина // Результаты испытания новых и усовершенствованных технологий, моделей и методов гидрометеорологических прогнозов. -М., 2017. - Т. 44. - С. 136-151.
- Кошелева, Е.Д. Краткосрочное прогнозирование уровней воды реки Обь у города Барнаула во время половодья 2018 года / Е.Д. Кошелева, А.В. Кудишин // Известия Алтайского отделения Русского географического общества. - 2018. - Т. 3, № 50. - С. 27-37.
- Землянов, И.В. Краткосрочный прогноз уровней воды в устьевой области р. Дон на основе гидродинамического моделирования / И.В. Землянов, А.Е. Павловский, И.Ю. Милютина, О.В. Горелиц, А.А. Сапожникова // Водные ресурсы. - 2022. - Т. 49, № 5. -С. 596-607.
- Филиппов, Ю.Г. Об одном способе расчета морских течений / Ю.Г. Филиппов // Труды государственного океанографического института. - М., 1970. - Т. 103. - С. 87-94.
- Корень, В.И. Математические модели в прогнозах речного стока / В.И. Корень. -Л: Гидрометеоиздат, 1991.
- Чикин, А.Л. Об одном из методов расчета параметров течений в водоемах с большой неоднородностью глубин / А.Л. Чикин // Водные ресурсы. - 2005. - Т. 32, № 1. -С. 55-60.
- Чикин, А.Л. Сгонно-нагонные колебания уровня воды устьевой области Дона: численное моделирование и сценарии изменения / А.Л. Чикин, А.В. Клещенков, Л.Г. Чикина, А.М. Коршун // Наука юга России. - 2017. - Т. 13, № 3. - С. 39-49.


