Моделирование контакта толстого упругого слоя на основании винклеровского типа переменного уровня с вертикальной стенкой
Автор: Богульский И.О.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Технические науки
Статья в выпуске: 4, 2018 года.
Бесплатный доступ
В работе исследуется поведение толстого ле-дяного поля, плавающего на поверхности воды, вблизи плоского вертикального участка берега или сооружения при перепадах уровня воды в водо-еме. Ледяное поле рассматривается в рамках мо-дели плоской деформации как толстая полубеско-нечная упругая пластина на основании винклеров-ского типа при различных вариантах контакта с берегом. Натурные наблюдения и эксперименты свидетельствуют, что даже при небольшом, по-рядка 10 см, понижении уровня воды в водоеме либо повышении его (подпоре) вблизи берега в толстом ледяном поле возникают значительные напряже-ния. При этом существенным оказывается влия-ние льда (толщиной порядка метра и более) на береговые сооружения, опоры мостов и др. При понижении уровня воды вблизи берега возникает так называемый «зависающий участок» - область сильно напряженного льда. Дальнейшее изменение уровня воды (20 см и более) обычно приводит к хрупкому разрушению в этой области - возникно-вению трещин. Оценка этой «опасной зоны» чрез-вычайно важна для планирования различных работ со льда, прокладки зимников и т.д. С помощью рас-четов, натурных наблюдений и экспериментов возможно моделировать природу контакта ледя- ного поля с берегом или сооружением. Сформули-рована и решена приближенно методом, основан-ным на аппроксимации неизвестных функций поли-номами Лежандра, стационарная задача о напря-женно-деформируемом состоянии полосы льда вблизи берега при понижении уровня воды. Рас-смотрены случаи полосы, свободной от внешних нагрузок и нагруженной внешней силой. Полученное решение вполне удовлетворительно качественно и количественно согласуется с натурными наблю-дениями и экспериментами. А именно - прослежи-вается возможность появления трещины в месте контакта льда с берегом. Натурный эксперимент проводился в порту Дудинка. Во время разгрузки барж, вмороженных в толстый (0,6-0,8 м) лед, фиксировалось изменение профиля ледяного поля во время всплытия баржи до и после возникновения трещины.
Численное моделирование, упругая пластина, ортогональные полиномы, вин-клеровский тип
Короткий адрес: https://sciup.org/140224426
IDR: 140224426 | УДК: 539.3+532.5
Текст научной статьи Моделирование контакта толстого упругого слоя на основании винклеровского типа переменного уровня с вертикальной стенкой
Введение . Исследуется поведение толстого ледяного поля, плавающего на поверхности воды, вблизи плоского вертикального участка берега при перепадах уровня воды. Ледяное поле рассматривается в рамках модели плоской деформации как упругая пластина на основании винклеровского типа. Натурные наблюдения и эксперименты говорят о том, что даже при небольшом, порядка 10 см, понижении уровня воды либо повышении его (подпоре) вблизи берега в толстом ледяном поле возникают значительные напряжения. При этом существенным оказывается влияние льда на береговые сооружения, опоры мостов и др. [1].
При понижении уровня воды вблизи берега возникает так называемый «зависающий участок» – область сильно напряженного льда. Дальнейшее изменение уровня воды (20 см и более) обычно приводит к хрупкому разрушению в этой области – возникновению трещин. Оценка этой «опасной зоны» чрезвычайно важна для планирования ведения различных работ со льда, прокладки зимников и т.д.
В работе сформулирована и решена приближенно методом, основанным на аппроксимации неизвестных функций полиномами Лежандра, стационарная задача о напряженно-деформируемом состоянии полосы льда вблизи берега при понижении уровня воды. Полученное решение вполне удовлетворительно качественно и количественно согласуется с натурными наблюдениями и экспериментами. Натурный эксперимент проводился в порту Дудинка. В о время разгрузки барж, вмороженных в толстый (0,6–0,8 м) лед, фиксировалось изменение профиля ледяного поля во время всплытия баржи до и после возникновения трещины.
Цель исследований . Моделирование контакта толстого упругого слоя на основании винклеровского типа переменного уровня с вертикальной стенкой.
Постановка задачи . Рассматривается задача о напряженно-деформируемом состоянии ледяного поля вблизи плоского участка берега. Ледяной слой моделируется тяжелой полубесконечной пластиной (рис. 1), ограниченной с одной стороны прямолинейным участком берега. Пластина плавает на воде, т.е. находится на упругом основании (винклеровско-го типа). К верхней поверхности может быть приложена нагрузка. Координата X направлена вдоль пластины и отсчитывается от берега, координату У будем отсчитывать от нижней поверхности. Таким образом, имеем задачу о плоской деформации упругого слоя.
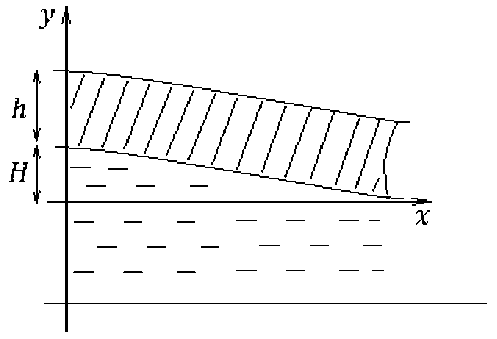
Рис. 1. Полубесконечный упругий слой
Натурные наблюдения показывают, что разрушение происходит уже при падении уровня на 20– 30 см при толщине полосы около метра. Следовательно, задачу можно рассматривать в рамках линейной теории упругости, пренебрегая нелинейными членами, связанными с большими поворотами.
да, дт^
+ =0; дх ду ди ди
Математическая формулировка имеет вид:
в области D ={0≤ У ≤ℎ,0≤ х ≤ ∞ } определить компоненты тензора напряжений ог , °2 , Т12 и вектора смещений U и V , удовлетворяющих уравнениям равновесия и закону Гука:
£Чг дх ди
до2
+ + ху =0; ду у
ди
ди ди.
^i = + ^ч~ ; f2 = +а —; fl =( + ), дх ду дх ду ду дх
где a= +2p;P= ; иp – упругие постоян ные Ламе; X – проекция плотности массовых сил на ось У. Неизвестные функции удовлетворяют граничным условиям на поверхностях У=0 иУ=ℎ.
На нижней поверхности отсутствует трение, и пластина лежит на упругом основании
T12 | у=о =0, ^2 | у=о =- Хус ( v | У-0 - к ℎ)․
На верхнюю поверхность действует нагрузка
Т12 |y-h = ∗(X), f2 = ∗(X), где т ∗, о∗ – заданные функции.
Рассмотрим задачу со свободной от нагрузки верхней поверхностью. В предыдущих формулах ℎ – толщина льда; с – отношение плотностей воды и льда; к = ; Н – перепад уровня воды.
Потребуем, чтобы при X → ∞ неизвестные функции были ограничены. На левом торце должно быть выполнено одно из условий:
-
а) °1 = ∗, Т12 = ∗2 – задана нагрузка, приложенная к торцу;
-
б) V = ∗ , u= и ∗ – задано смещение торца;
-
в) °1 = ∗, V = ∗ – смещение по У и распре
деленное по торцу усилие;
-
г) Т12 = ∗2,u= и ∗ – смещение торца и касательные напряжения заданы.
В рассматриваемой модельной задаче примем:
с=0,9; р = 103 кг/ м 3; ср =3980 м ; cs =1990 м/с . Далее у нас будет возникать малый безразмерный параметр ь ~0,02 и при решении задачи величинами порядка b будем пренебрегать по сравнению с единицей.
Метод и результаты решения . Задача решается приближенным методом [2, 3], позволяющим свести ее к краевой задаче для обыкновенных дифференциальных уравнений, основанным на разложении неизвестных функций в ряды по толщине по полиномам Лежандра.
В качестве первого приближения примем следующее разложение по толщине для неизвестных функций:
fi = ( z )+ d^ ( z ), ^2 = ( Z )+ Ч1Р1 ( z ),
T12 = ( z )+ S^l ( Z )+ S2P2 ( z ) , U = ( Z )+ ^P1 ( Z )+ V2^2 ( z ),
U = ( z )+ U± Pl ( z )+ U2P2 ( Z )+ изРз ( Z )․
Здесь переменная
z
=
y/h,0
Как отмечено в [4], представление напряжений и смещений в виде рядов по полиномам Лежандра является существенным преимуществом по сравнению с представлением в виде рядов по каким-либо другим функциям. Первые члены рядов имеют вполне конкретный физический смысл, а именно: , , пропорциональны усилию, моменту и пе ререзывающей силе.
Будем удовлетворять системе уравнений упругости интегрально:
h ^) ® d y = 0 , +1 + ■■ = 0,
∫ ( - - )( ) =0,∫ ( - - )( )=0,
Л)
=0 ․
∫( -2){
Деформации , , принимаются в следую- щем виде:
= ( + ), = ( + +), ох оу
2^ 12 ^ 0 P 0 )+^-(uopo+ U i 1+ u2 P2+ u3P3y
Возникает система обыкновенных дифференци- не вызывает проблем. В результате решения полу-альных уравнений шестого порядка, и ее решение чим v0 = ebbp[[ic cos(bp%) + c2sin(b px)] — H,d0 = 0, v0 = b bb bp[[(cp — C) ) cos(bpx) + (c2 + q)sin(h px)], dt = 6pp.b2ebbp[[c2 cos(bpx) — c1sin(ipx)] , s0 = —2ppb3ebbpx[(c1 — c2 )cos(bpx) + (c2 — c1)Sin(b px)].
Окончательно необходимо определить q и c2 с помощью известных при x = 0 граничных условий.
Варианты контакта льда с берегом:
-
а) предположим, что полоса льда «примерзла» к абсолютно твердой стенке, т.е.
V o (0) = 0, и 1 (0) = 0.
Тогда v0 = H [e~bpx(cos(bpx) + sin(bpx)) — 1], dt = 6ppb2Hebppx[cos(bpx) — sin(bpx)].
Растягивающее напряжение ^(x) будет наибольшим на поверхности у = h при x = 0 - в месте заделки (рис. 3, кривая а). Как показывают наблюдения, именно здесь и происходит образование первой трещины. Смещение v(x) = H + v 0(x) приведено на рисунке 2 (кривая а);
-
б) «свободно опертый торец»
Пусть v0 = 0, d 1 = 0, тогда c1 = H ,c2 = 0, v0 = H [ bbppx cos(bpx) — 1], dt = 6ppb2Hbbpxx sin(b px).
В этом случае растягивающее напряжение ^(х) будет наибольшим на ни жней поверхности = 0 на расстоянии x * = - 4 — h ~ 18^ 19h от стенки √
(рис.3, кривая б). Смещение v(x) приведено на рисунке 2 (кривая б).
Таким образом, при дальнейшем падении уровня воды возможно возникновение второй трещины на расстоянии 18 ^ 19 толщин льда от стенки.
Можно предположить, что осуществляется упругий контакт со стенкой, обусловленный ее податливостью;
-
в) «упругий контакт»
При = 0 принимаем = 0,(0) =
Рщ (0), 0 < f>< ™ .
Тогда
= , = = ,0≤≤1․
-
6+
v 0 = H [eb ppx(cos(b px) + a sin(b px)) — 1], d p = 6 pp b2 He bppx[acos(b px) — sin(b px)].
Момент и перемещение приведены на рисунках 2, 3 (кривые в).
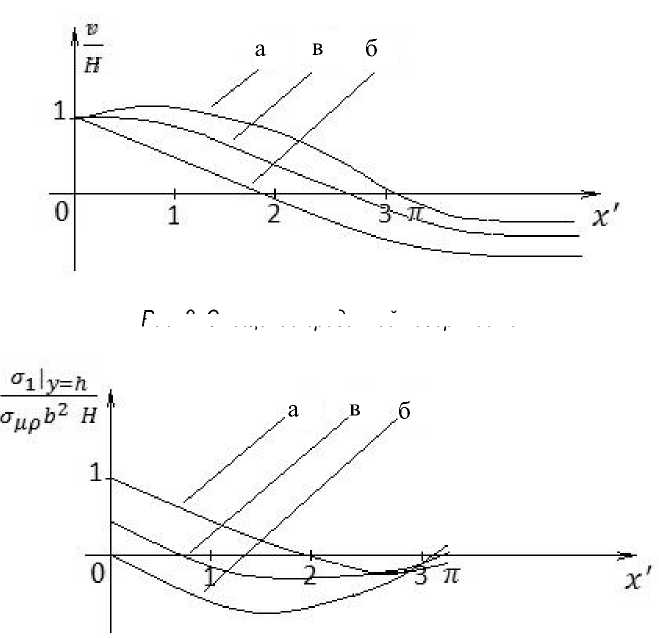
Рис. 3. Растягивающие напряжения в пластине
Рис. 2. Смещение срединной поверхности
Деформация ледяного поля с учетом внешней нагрузки . В практических задачах представляет интерес расчет напряженно-деформируемого состояния «зависающего» участка льда с дополнительно приложенной нагрузкой на поверхности у = h. Расчет таких задач удобнее проводить, выделяя область с реальной нагрузкой, требуя сопряжения решения с решением в соседних областях.
Пусть на поверхности у = h действует сила F, равномерно распределенная по отрезку [Ьг,L 2] (рис. 4). Задачу о деформации ледяного поля формулируем следующем образом.
В области DI = {0 <у < h,0 < х < LJ определить функции напряжения и перемещения, удовлетворяющие уравнению упругости.
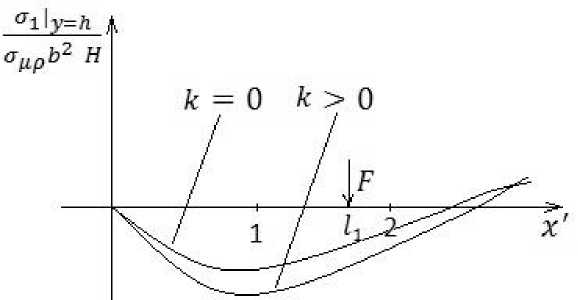
В области Dn= {0 <у Рис. 4. Пластина под внешней нагрузкой При X= иX= выполнены условия сопряжения решений. В итоге получаем: = ℎ ' ' + ℎ ' ' + ℎ ' '+ ℎ '' V" = ℎX cosx'+K2cℎX ' sin X'+K3sℎX'cosx'+K4sℎX'sinx ' –, = ℎ ' '+ ℎ ' '+ ℎ ' '+ ℎ '' где V(X)=H+ vo (X), X'=bpx, ^1 = , ^2 = ,к Hgph ll[=-b [(C^ + C3 )cℎX cosx+(C4 - Cl )cℎx sinx+(Cl + C4 )SℎX cosx+(C2 - C3 )sℎX cosx], d[=6ppb2 [c4cℎX cosx - C3Cℎx sinx + c2sℎX cosx - c[sℎX cosx], so =-2ppb3 [(C2 - C3 )cℎX cosx-(c4 + C1 )cℎx sinx-(C1 - c4 )sℎX cosx+(C2 - C3 )sℎX cosx]․ Здесь r=1,2,3,ci = , = = , = , =- , =1,2,3,4․ Десять неизвестных констант определяются из условия сопряжения. Наиболее простым, но интересным вариантом приложения нагрузки к поверхности У=ℎ является случай действия сосредоточенной в точке силы. Пусть l^ → ^2 , при этом сила F остается постоянной. Перейдя к пределу по ^ 1→ ^2 , получим решение задачи о деформации упругой пластины под действием сосредоточенной силы. Если условия на торце соответствуют задаче б, получаем C4=0,C1 = , C2 = (cosl4 - sinl4), C3 =-H- kHe~h(cosl4 + sinl4) ․ V1 (X)= = + kHe~h [(cosl4 - sinl4 )cℎx sinx-(cosl4 + sinl4)sℎX cosx], V111 (X)=He Xcosx + +kHe~x[(cℎ li sin h. -sℎ l4cosl4) cosx-(cℎ11 sin 11 +sℎl4cosl4) sinx]․ Поперечное смещение точек пластины приведе- В случае, если край пластины «вморожен» в но на рисунке 5. жесткую стенку, получаем Распределение по длине напряжения – на рисун ке 6. с2+ C3 =0,C1 = , C3 =-H- kHe~h (cosl4 + sinl4), C4 = + kHe~1^ (cosl4 + sinl4), C4=-H-2kHe~1^ sin ^1. ․ Рис. 5. Поперечное смещение пластины Рис. 6. Распределение напряжений по длине полосы Выводы. Таким образом, можно сделать вывод, что растягивающее напряжение на верхней поверхности ледяного поля в месте заделки льда в берег не зависит от действия сосредоточенной силы F, если она приложена в точках Ii = яп, п = 0,1,... И наоборот, наибольшее влияние на растягивающие напряжения в месте заделки оказывает сосредоточенная сила, приложенная к поверхности льда в точке Iг = ^, т.е. на расстоянии приблизительно 18 ^ 19 толщин льда от берега. Заметим, что это расстояние совпадает с «опасным» расстоянием, полученным в задаче о деформации свободной от нагрузок полосы льда со свободно опертым торцом.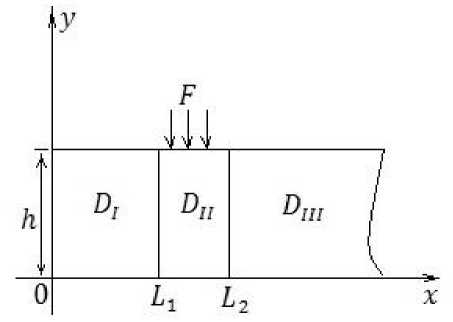
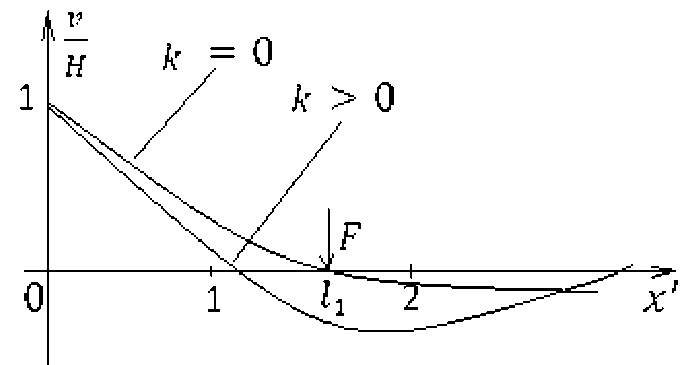
Список литературы Моделирование контакта толстого упругого слоя на основании винклеровского типа переменного уровня с вертикальной стенкой
- Богородский В.В., Гаврило В.П. Лед. -Л.: Гидрометеоиздат, 1980. -385 с.
- Иванов Г.В. Решение плоской смешанной задачи теории упругости в виде рядов по полиномам Лежандра//Прикладная механика и техническая физика. -1976. -№ 6. -С. 27-34.
- Кикоин И.К. Таблицы физических величин. -М.: Атомиздат, 1976. -1005 с.
- Иванов Г.В. Теория пластин и оболочек: учеб. пособие. -Новосибирск, 1980. -84 с.


