Моделирование контактного режима работы атомно-силового микроскопа с учетом немеханических сил взаимодействия с поверхностью образца

Современные нанотехнологии, применяемые в материаловедении, не осуществимы без достоверного знания внутренних механизмов, действующих на надмолекулярном уровне (когда среду еще можно считать континуумом, но уже необходимо учитывать эффекты, связанные с особенностями молекулярного строения вещества). Научившись эффективно управлять процессами и явлениями на этих структурных масштабах, можно целенаправленно создавать новые материалы с потребительскими свойствами, принципиально не достижимыми в рамках традиционных технологий.

На сегодняшний день атомно-силовая микроскопия (АСМ) является одним из самых перспективных направлений в изучении структуры материалов на наномасштабном уровне. Размеры и стоимость таких микроскопов значительно ниже, чем электронных, а возможностей намного больше [1]. Они более устойчивы к воздействию температуры и электромагнитного излучения, способны работать в вакууме, воздушной и жидкой средах. С помощью АСМ можно исследовать самые разнообразные материалы: проводящие, диэлектрические, биологические и так далее без существенного повреждения объекта и трудоемкой подготовки его поверхности. Но самое главное — АСМ позволяет извлекать информацию не только о геометрии, но и о механических особенностях строения материала на наноуровне [2–5]. Она успешно применяется при измерении упругого модуля [6, 7], параметров упрочнения [8] и ползучести [9] а также других характеристик на уровне наноструктуры. Данная методика позволяет непосредственно наблюдать такие микропроцессы, как появление дислокаций, возникновение сдвиговой нестабильности, фазовые переходы и многие другие явления, не доступные для ранее известных технологий [10].

В процессе эксперимента зонд АСМ сканирует выбранный участок поверхности образца. Получаемые при этом экспериментальные данные представляют собой зависимости между координатами точек

сканирования, силой реакции, действующей на зонд, глубиной вдавливания вершины зонда в исследуемый материал и отклонением конца консоли зонда [11]. Эти результаты сами по себе (без дополнительных сведений о предмете исследований) малоинформативны, поэтому требуется их дальнейшая теоретическая расшифровка с привлечением различных физических и механических моделей. Построение таких моделей — важная фундаментальная задача. Существуют два основных подхода к ее решению:

– исследуемый материал представляется в виде молекулярной решетки, которая деформируется под воздействием зонда — «атомарные» модели [12–13]. К их недостаткам можно отнести большие объемы требуемых вычислений, а также значительные трудности с моделированием поведения сложных сред (упругопластических, вязкоупругих и так далее);

– с использованием гипотезы континуума и классических методов решается (с теми или иными ограничениями и допущениями) задача механики сплошных сред [14–17]. Опыт показывает, что на масштабах порядка до 10 нм и выше среду допустимо считать сплошным континуумом, и такое предположение является обоснованным.

В данной статье предложена модель, описывающая взаимодействие поверхности нелинейно-упругого полимерного материала и кантилевера АСМ при контактном режиме работы. При этом рассматривается не только механические силы, возникающие между зондом АСМ и образцом, но и другие, имеющие немеханическую природу. На наноуровне их влияние на общую картину взаимодействия может быть очень существенным.

• 2.    Расчетная схема модели

Расчетная схема модели состоит из последовательно соединенных пружинных элементов 1 и 2 (Рис. 1).

Элемент 1 (чисто упругий) моделирует механическое воздействие кантилевера АСМ ( F cant = F 1 ). Элемент 2

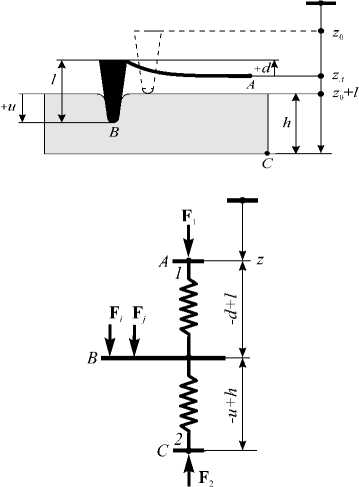
Рис. 1. Расчетная схема модели «зонд АСМ – полимерный образец»

отвечает за механическую реакцию F mech = F 2 образца на внедрение в н е го зонда АСМ; он может быть линейно- или нелинейно упругим, вязкоупругим, упругопластическим, упруговязкопластическим и так далее. Все зависит от того, какой конкретный материал подвергается испытанию. Механическую силу F _mech можно определить из решения соответствующей контактной краевой задачи.

Кроме механической силы между зондом и образцом действуют силы межмолекулярного взаимодействия (силы Ван-дер-Ваальса) и силы поверхностного натяжения. В случае действия других, имеющих немеханическую природу сил (адгезионных или капиллярных сил, сил электростатического и магнитного взаимодействия) модельная схема не содержит каких-то принципиальных ограничений для их учета.

В дальнейшем, так как фактически решается одномерная задача, вместо векторов сил F _i ( i — номер «силы») используются их проекции на ось z — F i ( F_s = F i ■ n z ).

В соответствии с выбранной схемой ось z, вдоль которой движется зонд АСМ, направлена вниз. Определим глубину вдавливания зонда в образец u и вертикальное отклонение кантилевера d так, чтобы при внедрении зонда в образец они имели положительные значения, а в случае зазора между ними — отрицательные:

u = zB-(z0 +1), d = zA-(zB -1), Az = zA -z0 = u + d ,

где l — высота зонда, h — толщина образца, z ₀ — координата точки закрепления кантилевера A на оси z в момент, когда она удалена от поверхности образца на расстояние l (то есть координата положения недеформированного кантилевера в момент касания поверхности образца).

• 3.    Моделирование механического взаимодействия между зондом АСМ и образцом

Зависимость силы на вершине зонда кантилевера Fcant = F1 от изгиба консоли зададим через смещение ее свободного конца d относительно точки закрепления. Так как длина консоли во много раз превышает высоту зонда l, то можно считать, что эта сила направлена строго по нормали к поверхности образца и направлена вдоль оси z, то есть латеральная (поперечная) составляющая пренебрежимо мала. Для расчета Fcant используется стандартная формула

Fcant   kspr d , где kspr — спринг-константа зонда, устанавливаемая заводом-изготовителем. Таким образом, элемент 1 является линейно-упругой конечно-деформируемой пружиной.

Элемент 2 отвечает за механическую реакцию F_mech = F ₂ исследуемого образца на внедрение в него зонда АСМ. На данном этапе исследований считаем, что материал образца нелинейно-упругий F mech = F el . Таким образом, контактная задача внедрения зонда АСМ в полимерную поверхность решается в нелинейно-упругой осесимметричной постановке. Полагаем что зонд (который обычно представляет собой кремниевый кристалл) — абсолютно жесткое тело, а механическое поведение полимера описывается с помощью упругого потенциала для неогукового материала:

w = C T ( tr B - 3 ) ,                                              (3)

где C_T — упругая константа Трелоара, равная половине начального модуля сдвига, B — левый тензор

Коши–Грина в полярном разложении деформационного градиента среды.

Зонд представим в виде конуса со скругленной вершиной радиусом R . Угол α между осью конуса и образующей составляет 20°. Модельные образцы имеют вид круглых «таблеток» радиусом R L и толщиной h .

После возникновения контакта на границе соприкосновения зонда и образца выполняется условие полного прилипания. Причиной выбора данного условия послужили множественные опыты (в том числе и проведенные автором лично), в которых при внедрении зонда АСМ в эластомер наблюдалось его прилипание к поверхности — на обратном ходе материал некоторое время «тянется» за удаляющимся зондом. Нижняя граница образца находится в полном контакте (без отрывов и проскальзывания) с абсолютно жесткой плоскостью. Сверху на зонд действует сосредоточенная сила F cant .

Для реализации применялся метод конечных элементов. Расчетная схема приведена на рисунке 2. При вычислениях геометрические параметры варьировались в пределах: R — от 10 до 50 нм; R_L — от 200 до 500 нм; h — от 100 до 500 нм. Для каждой конкретной геометрии краевая задача решалась несколько раз. При этом сетки различались как количеством узлов, так и типом элементов; использовались четырехугольный 8-узловой и треугольный 6-узловой изопараметрические конечные элементы. Сетка строилась со сгущением в направлении от внешней границы образца к точке начального контакта зонда с поверхностью. Заметим, что при одном и том же количестве узлов точность решения, получаемая на обоих типах сеток, была примерно одинаковая. Однако треугольные элементы оказалось более выгодными с точки зрения

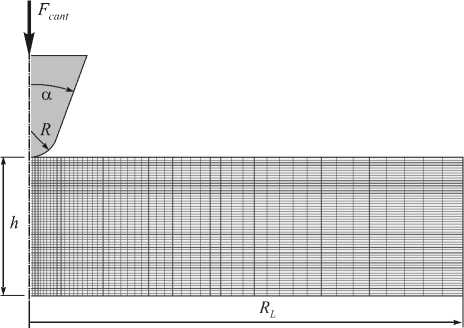
Рис. 2. Расчетная     конечно-элементная     схема осесимметричной задачи внедрения зонда атомно-силового

устойчивости алгоритма (задача рассматривалась в приращениях в рамках теории больших деформаций) и затраченного на решение времени. При максимальном размере образца (RL = 500 нм и h = 500 нм)

конечно-элементная сетка содержала примерно 4000 элементов и 17000 узлов. Следует отметить, что максимальная глубина внедрения зонда, при которой удалось получить корректное решение задачи при численной реализации, составила 3,8 R .

В результате получено соотношение между упругой силой реакции Fel , глубиной вдавливания зонда в образец u, жесткостью образца CT (3), толщиной h, а также радиусом скругления вершины зонда R. Для удобства дальнейших расчетов оно аппроксимировалось в виде аналитической функции [18]. В случае, когда h намного превышала R (когда влияние жесткой подложки несущественно), эта зависимость имела вид:

F el /( C t R 2 ) = 8,6 ( uR ) ^1,3.

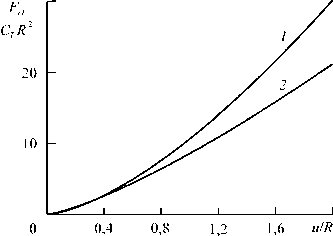
Рис. 3. Зависимости силы реакции F_el , действующей на зонд, от глубины его вдавливания в материал u для бесконечного слоя h ; кривая 1 – формула Герца, 2 – численное нелинейно-упругое решение

На рисунке 3 представлены зависимости силы реакции F_el , действующей на зонд, от глубины его вдавливания в образец, рассчитанные по формуле Герца (линейно-упругая задача о контакле двух сфер) [19] и численно (неогуковый материал). Для несжимаемой среды, когда одна из сфер имеет бесконечно большой радиус, а вторая — абсолютно жесткая радиусом R (контакт с плоским полупространством), формула Герца записывается в виде ( G — модуль сдвига)

F^ = 16 GR^1/2 u ^3/2/3. (5)

Из графиков видно, что расхождение результатов, найденных по формуле (5) и из нелинейно-упругого решения (4), начинается при u/R >  0,4. Таким образом, при меньших значениях отношения uR формулу (5) вполне можно использовать для определения силы реакции, если исследуемая среда гомогенна по механическим свойствам.

• 4.    Силы Ван-дер-Ваальса (межмолекулярное взаимодействие)

Опыт показывает, что взаимодействие между зондом и полимером возникает еще до того, как между ними произойдет контакт. Одним из возможных объяснений этому может служить влияние сил Ван-дер-Ваальса, которые на определенном расстоянии начинают притягивать зонд АСМ к поверхности образца.

Точно рассчитать межмолекулярные силы на основе квантовой механики при огромном разнообразии пар молекул, участвующих в процессе, практически невозможно. Поэтому обычно подбирают такую формулу для потенциала взаимодействия U , чтобы проделанные с ее помощью расчеты хорошо согласовывались с экспериментом [20–21]. Соответствующая сила определяется через потенциал как

F = - grad U .

Зададим энергию ван-дер-Ваальсового взаимодействия двух атомов, находящихся на расстоянии r друг от друга, через потенциал Леннарда-Джонса

U ( r ) = U0 {(ro/r )12 - 2 ( ro/r )6 } + U» = 4Uо {(r /r )12 -(r /r )6 }+ U» , где r0 — равновесное расстояние между атомами, соответствующее минимальному значению энергии системы U0 (или глубине потенциальной ямы, то есть размеру области U (r) < 0); U„ — энергия взаимодействия между атомами при r ^ да (обычно принимается U„ = 0 ); г* — наименьшее возможное расстояние между атомами (когда U (r) снова становится равной U„).

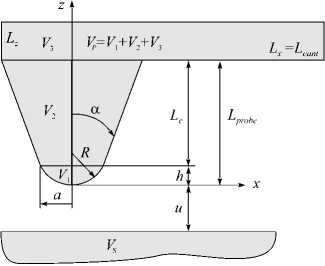
Рис. 4. Расчетная схема для интегрирования U по объемам зонда и образца

Общую энергию, обусловленную силами ван-дер-Ваальсового притяжения, получим, суммируя элементарные взаимодействия для каждого из атомов зонда (индекс P ) и образца (индекс S ):

UPS = ff U(IrP - rs I)nP (rP )ns (rS )dVPdVS , (8) VPVS где nP и nS — плотности атомов в материале; rP и rS — радиусы-векторы точек; VP и VS — объемы. Если представим зонд АСМ как составное тело, включающее сферический сегмент, усеченный конус и параллелепипед, а образец будем рассматривать как бесконечное плоское полупространство, то интеграл (8) в случае действия только силы притяжения берется аналитически. Расчетная схема для интегрирования показана на рисунке 4.

Силу взаимного притяжения сферического сегмента V 1 и полупространства V_S вычислим по формуле:

w

F ₁

dU         ² h ² ( Rh + 3 Ru - hu )

¹ = + K_PS--^--------------^

du ^PS 6        ^{2        3}

где K PS - K * n_Pn_S , K * --2 U 0 r ₀ ⁶ =- A H — константы взаимодействия ( K * — константа Гамакера c обратным знаком). Для усеченного конуса (сегмента V ₂) и полупространства V_S ( u c - u + h , a - R cos a) имеем:

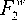
dU-,       П

- - + K PS — du_c          6

tg a

L ³ c

uc (Lc + uc )3

+ a tg a

L c ( L c + 3 u c ) u 2 ( L_c + u_c ) 3

для консоли (сегмента V ₃) и полупространства V S ( u p - u + L probe ):

F 3 ^w

dU 3 _ v ^K_{T T T} ⁽ 3 L z u p ^{+ 3 u}P ⁺ L z )

-       - + KP^ LYLVL7              1 dup         ⁶            uP ( Lz + up ) 3

Отклонение свободного конца кантилевера получим из решения задачи изгиба защемленной консольной балки (Рис. 5) при условии, что по всей длине балки действует равномерно распределенная нагрузка q w , а к свободному концу приложена сосредоточенная сила F w : F w - F w + F -W , q w - F 3w^ L x. .

Рис. 5. Схема определения прогиба консоли зонда АСМ под действием сил ван-дер-Ваальсового притяжения

Прогиб консоли d и соответствующая спринг-константа kspr (2) будут равны d--[qwL4/8 + FWL3/3]/(EJ),   J - JJz2dS -LyL3/12,    kpr - Fw/d .

S

При моделировании воздействия сил межмолекулярного притяжения было рассмотрено два типа кантеливеров АСМ: мягкий — для контактного режима работы, и более жесткий — для полуконтактного (когда зонд не вдавливается в образец с некоторой силой, а колеблется с заданной частотой, «постукивая» поверхность). Геометрические и механические характеристики зондов приведены в таблице 1 (реальные размеры для промышленных зондов типа FESP(W) фирмы Nanoprobe, Digital Instruments, USA).

Таблица 1. Геометрические и механические характеристики зондов

Характеристики зонда	Полуконтактный режим	Контактный режим
L cant	200,00 мкм	225,00 мкм
L z	7,00 мкм	2,50 мкм
L y	43,00 мкм	30,00 мкм
L probe	14,00 мкм	15,00 мкм
R	0,01 мкм	0,01 мкм
α	20º	20º
k spr	73,4 нН/нм	1,68 нН/нм

Материал консоли и зонда — кремний с модулем Юнга E - 160 ГПа - 160нН/нм². Модельный «образец» представлял собой неогуковый материал с модулем сдвига G = 1,0 МПа. Толщина образца составляла 100 нм. При расчетах значения K_PS и r ₀ принимались равными 0,01 нН·нм и 0,2 нм соответственно [22, 23].

Расчеты показали, что основной вклад в формирование ван-дер-Ваальсовых сил межмолекулярного притяжения дает взаимодействие между сферической вершиной зонда АСМ и исследуемым образцом. В таблице 2 приведены соответствующие значения сил F ₁ ^w , F ₂ ^w и F ₃ ^w (шаровой сегмент, усеченный конус и консоль соответственно). Различия между F ₁ ^w и F ₂ ^w варьируются в пределах от одного до трех порядков, в то время как величина F ₃ ^w в миллион раз меньше F ₁ ^w , несмотря на то, что масса консоли по сравнению с массой зонда просто огромна. Это вполне объяснимо, так как минимальное расстояние консоли от поверхности образца ограничивается высотой зонда, то есть ≈ 3 - 15мкм (что на несколько порядков превышает диапазон действия сил Ван-дер-Ваальса).

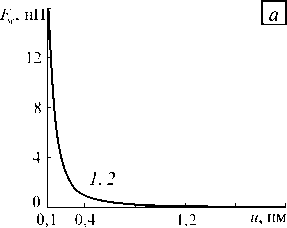
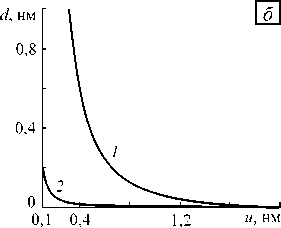
Таблица 2. Зависимости сил Ван-дер-Ваальса от расстояния до поверхности для различных частей зонда

Расстояние до поверхности u , нм	Шаровой сегмент	Усеченный конус	Консоль
	F 1 w , нН	F 2 w ⋅ 103, нН	F 3 w ⋅ 106 , нН
0,100	16,28	1,587	3,877
0,245	2,670	1,527	3,877
0,515	0,585	1,424	3,877
0,755	0,264	1,342	3,877
0,995	0,148	1,268	3,876
1,205	0,098	1,208	3,876
1,505	0,060	1,130	3,876
1,745	0,043	1,073	3,876
2,000	0,032	1,021	3,876

Рис. 6. Зависимости силы Ван-дер-Ваальса ( а ) и прогиба конца консоли ( б ) от расстояния между поверхностью образца и кончиком зонда: мягкий кантилевер ( k spr = 1,68 Н/м) (кривая 1 ), жесткий кантилевер ( k spr = 74,3 Н/м) ( 2 )

На рисунке 6 представлены зависимости силы F_w и прогиба конца консоли d от расстояния между поверхностью образца и вершиной зонда u для «мягкого» и «жесткого» кантилеверов. Из графиков видно, что в случае «жесткого» кантилевера (полуконтактный режим работы АСМ) силы Ван-дер-Ваальса слабо влияют на изгиб ввиду его недостаточной «чувствительности» и ими можно пренебречь. Иная картина наблюдается при контактном режиме («мягкий» кантилевер). В этом случае силы межмолекулярного притяжения могут вызвать заметное отклонение конца консоли, и это необходимо учитывать при обработке экспериментальных данных. Также можно сделать вывод, что межмолекулярные силы начинают действовать на расстояниях, не превышающих 1–2 нм, и не могут служить объяснением того факта, что в некоторых экспериментах отклонения катилевера АСМ наблюдаются при значительно больших значениях u (порядка 3 нм и более). У этого явления, возможно, другая природа. Вероятно, это связано с наличием на поверхности сверхтонкой водяной пленки, касание которой и вызывает втягивание зонда АСМ. Могут быть и иные причины, но их выяснение выходит за рамки настоящего исследования.

• 5.    Поверхностные силы сопротивления внедрению зонда

Наряду с обычным механическим сопротивлением внедрению зонда АСМ в исследуемую поверхность при переходе на наноуровень существенную роль начинают играть силы поверхностного натяжения. Они зависят от кривизны поверхности и при очень малых радиусах могут давать весомый вклад в общую картину взаимодействия «зонд–образец». В соответствии с формулой Лапласа дополнительное поверхностное давление, действующее на элементарный участок поверхности, которую можно представить как часть эллипсоида, определяется как

∆p =βρ1+βρ2,

где ρ₁ и ρ₂ — радиусы кривизны двух взаимно перпендикулярных нормальных сечений к поверхности в данной точке; в — коэффициент поверхностного натяжения (или плотность свободной энергии поверхностного натяжения). Например, для воды при 20°С в = 0,0728 Н/м [24], то есть для капли радиусом 10 нм дополнительное поверхностное давление составляет: A p = 14,56 ■ 10 ^{- 3} МПа, тогда как для капли R = 1 мм A p = 0,1456 ■ IO ^{- 3} МПа! Принято считать р i положительным, если центр кривизны соответствующего сечения лежит внутри тела. Для плоской поверхности ρ _i равно бесконечности, то есть поверхностное давление отсутствует. При расчетах полагалось, что в = 0,15 Н/м (как для хорошо смачиваемых сортов резин) [25].

Считая, что зонд состоит из шарового сегмента и усеченного конуса, силу поверхностного натяжения F ₁ ^s , обусловленную вдавливанием зонда в образец, можно рассчитать аналитически, проинтегрировав формулу Лапласа (10) по поверхности контакта. Тогда сила поверхностного натяжения F ₁ ^s на сферической поверхности равна:

F1 s = 2пвR (2u/r - и2/R2), и < h = R (1-sin а).

Формула, связывающая силу, действующую на поверхности контакта, с геометрическими параметрами конической части зонда, имеет вид (а — половина угла раскрытия конуса):

F 2 = 2 nPA z ( A _а / В а ) sin а tg а ,

1/2

где A _а = tg2 а/ ( 2cos а ) , В _а =^ 2tg а /cos а A _а ( 1 + A _а sin а ) - A ^ /cos ² а^ .

Таким образом, поверхностная сила на конусе пропорциональна глубине внедрения конической части зонда в материал и не зависит от расстояния, отделяющего эту часть от вершины конуса. Обусловлено это тем, что в какой мере увеличивается площадь, приходящаяся на единицу высоты конуса (то есть координаты z), при удалении от вершины, в такой же мере уменьшается величина Δ p , которая обратно пропорциональна радиусу кривизны ρ перпендикулярного к образующей конуса эллиптического сечения. Полная поверхностная сила F_s , действующая на зонд АСМ, равна сумме F ₁ ^s и F ₂ ^s .

• 6.    Моделирование взаимодействия зонда АСМ и поверхности образца

С помощью выше описанного подхода проведено моделирование контактного режима работы АСМ с учетом нелинейно-упругих, межмолекулярных и поверхностных сил. Характеристики зонда были следующими: радиус скругления вершины R = 10 нм, высота L probe = 15 мкм, половинный угол раскрытия конуса α = 20º. По сравнению с образцом зонд считался абсолютно жестким телом. При расчетах использовался «мягкий» кантилевер со спринг-константой k spr = 1,68 нН/нм. Модельным материалом служил высокоэластичный неогуковый материал с модулем сдвига G = 1,0 МПа.

При расчетах входным аргументом была величина u , которая задавалась пошагово от значения u_up (максимальное удаление зонда от поверхности образца) до u_in (максимальная глубина внедрения в материал). Из решения уравнения равновесия определялась результирующая сила реакции F = – F cant , через которую рассчитывались соответствующие значения смещения точки закрепления кантилевера АСМ Δ z и его вертикальное отклонение d (см. выражения (1) и (2)).

Следует отметить, что хотя задача и решалась в статической постановке, тем не менее проведена оценка устойчивости процесса приближения зонда к поверхности образца до возникновения контакта. То есть моделировалось влияние малых отклонений аргумента u на уравнения равновесия. Делалось это следующим образом. Уравнение равновесия до момента контакта имеет вид: F_cant + F w = 0. Если для текущего значения и придать зонду дополнительное малое вертикальное смещение б и вычислить возникающую при этом дополнительную малую, «стабилизирующую» силу δ F (с учетом того, что A z - ( d + s ) = б и , d + б = 5 d )

5F = Fw (Az-(d + Б)) + Fcant (d +Б) ,

то по ее направлению можно судить об устойчивости системы на данном шаге нагружения. Если направления б и 5F противоположны, то имеем систему с отрицательной обратной связью (реакция на малое возмущение стремиться его погасить) — система ведет себя устойчиво. В противном случае, когда направления б и 5F совпадают, получается система с положительной обратной связью (реакция на малое возмущение провоцирует его рост) — систем неустойчива.

На рисунке 7 представлена зависимость б F ( и ) для случая б = - 10 - 4 нм. Из ее анализа следует, что критическая точка соответствует и = и * = - 0,54 нм. При и <  и * ситуация устойчива, поскольку при и <  и * б F ( и ) = 0, то есть наблюдается неустойчивое равновесие, а при и >  и * происходит потеря устойчивости системы. В реальности это выражается в том, что происходит «скачок» кантилевера вниз, то есть в этом диапазоне нагружения надо решать динамическую задачу.

Были проведены численные расчеты, в которых дополнительное смещение зонда б варьировалось от 10 ^{- 5} до 10 ^{- 2} нм, а шаг по и изменялся от 0,001 до 0,01 нм. Значение и * (момент начала скачка) оставалось практически неизменным, что позволило сделать вывод о надежности полученных результатов. На рисунке 8 сплошной линией показана модельная зависимость силы реакции F , действующей на зонд в направлении от вершины зонда АСМ к исследуемой поверхности, от глубины вдавливания и ( и >  0, если зонд внедрен в образец, и и <  0, если контакт отсутствует). До контакта на зонд действует только сила Ван-дер-Ваальса F_w , при контакте добавляются упругая ( F_el ) и поверхностная ( F_s ) силы. Считалось, что после контакта сила F_w постоянна и равна максимальному значению, достигнутому на момент касания. Зависимость F s ( и ) показана на графике штрих-пунктирной линией. Зона потери устойчивости на кривой F ( и ) выделена штриховой линией.

На рисунке 9 приведены зависимости d и и от смещения точки его закрепления A z . Кружком отмечены значения, соответствующие моменту начала «скачка» зонда к поверхности. Как видно из графиков, они соответствует точкам перегиба кривых.

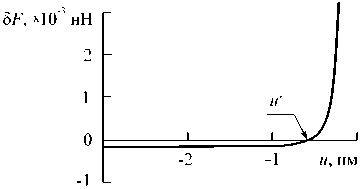
стабилизирующей силы  δF вершиной зонда и поверхностью

Рис. 7. Зависимость от расстояния между образца u

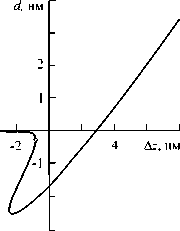
а

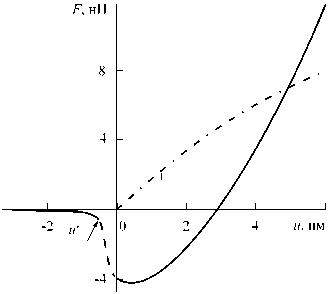
Рис. 8. Зависимость силы реакции F на зонде АСМ от расстояния между его вершиной и поверхностью образца u

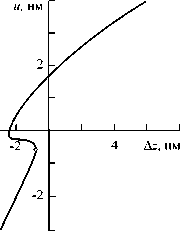
Рис. 9. Зависимости вертикального отклонения конца кантилевера d ( а ) и расстояния между вершиной зонда и поверхностью образца u ( б ) от смещения точки закрепления кантилевера Δ z

• 7.    Заключение

Предложена дискретно-механическая модель, позволяющая описывать взаимодействие поверхности нелинейно-упругого полимерного материала и кантилевера АСМ при контактном режиме работы. Кроме механической реакции от контакта между зондом и исследуемым материалом в модели учитывается также межмолекулярное взаимодействие Ван-дер-Ваальса и силы поверхностного натяжения, связанные с искривлением поверхности образца.

Полученные в работе аналитические зависимости между силами, действующими на зонд АСМ, и расстоянием вершины зонда до поверхности образца могут быть использованы другими исследователями при разработке программного обеспечения атомно-силовых микроскопов для расшифровки экспериментальных данных.

Работа выполнена при финансовой поддержке РФФИ и Министерства промышленности, инноваций и науки Пермского края (проект № 11-08-96001-р_Урал_а), а также Программы ОЭММПУ РАН 12-Т-1-1004.