Моделирование контактных деформаций в неподвижных соединениях несущей системы портального фрезерного станка

Жесткость неподвижных соединений базовых деталей существенно влияет на погрешности обработки. В общем балансе упругих перемещений несущей системы станка контактные деформации в стыках составляют от 30 до 70%. Линейная деформация δ и поворот φ в плоском стыке при нагружении центральной силой Р и моментом М (рис. 1) определяют из выражений:

m

5 = c\ — I

I S )

M

^Ф = MJ

где с, с м – коэффициенты контактной податливости; S, J – площадь и момент инерции сечения контакта; m – показатель степени (m=0,5 для поверхностей, и зависят от материала и качества обработки сопрягаемых поверхностей. Для деталей из стали и чугуна при чистовой обработке (тонком точении, шлифовании и тщательном шабрении) с = 0,15-0,2; при притирке можно получить с = 0,07, а при сравнительно грубой обработке (фрезеровании, грубом шабрении) с = 0,8-l,2.).

Коэффициенты контактной податливости связаны соотношением

Неподвижные стыки базовых деталей имеют, как правило, предварительную затяжку силами, значительно большими, чем силы резания. Это позволяет определять контактные деформации и угол поворота стыка по приближенным линейным зависимостям:

m - 1

5 = cmp 0 p ^,

Ф = cmp™-1M / J где р0, р — первоначальное и текущее кон- тактное давление в стыке [1].

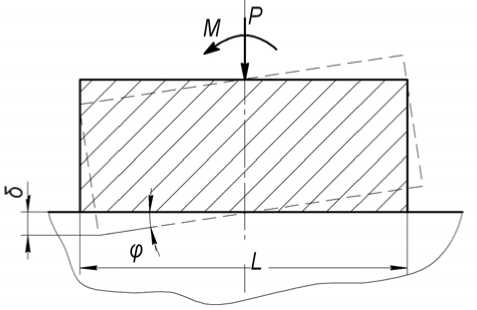
Рис. 1. Схема деформации плоского стыка при нагружении силой и моментом

c

m

cm

P

S

- 1

Точность приближенных расчетов оценивается сравнением результатов расчетов и экспериментов на реальных станках аналогич-ных конструкций при статическом нагружении, соответствующем нагружению при резании. Во многих случаях, когда базовые детали из-за сложности формы не поддаются расчету, проводят исследование жесткости на моделях, геометрически подобных рассматриваемому

элементу или базовой детали в целом. Обязательным условием при этом является равенство критериев подобия модели и реальной базовой детали [2]. Расчет деформаций и поворотов в плоском стыке по формулам (1-5) дает возможность приблизительно оценить жесткость неподвижных соединений при проектировании станочного оборудования. Основным допущением является расчет линейной деформация и поворота при нагружении центральной силой Р или моментом М, тогда как в реальной несущей системе станка, силы или моменты, действующие на стык, приложены иначе, что зачастую приводит к существенному усложнению задачи. В связи с этим принимается большое количество допущений и округлений, постоянные коэффициенты определяются из экспериментов, после завершения расчетов деформаций для использования в проектировании предстоит решить еще более сложную задачу – построение математической модели станка.

Для минимизации экспериментальных исследований с использованием сложного и дорогостоящего измерительного оборудования предлагается решение данной задачи методом конечных элементов средствами пакета ANSYS Workbench [3], который позволит более точно производить расчет контактных деформаций в стыках, основываясь на геометрической модели станка, свойствах материалов, принимать во внимание способы крепления деталей в стыке, не зависеть от количества самих стыков, кроме того, позволит моделировать приложение усилий в стыках более адекватно, с учетом силы резания. В ходе исследований был произведен расчет контактных деформаций в неподвижных соединениях несущей системы портального фрезерного станка с ЧПУ. Станок используется для обучения студентов основам программирования на станках с ЧПУ и для производства небольших по габаритам сложнопрофильных деталей [4]. Моделирование деформированного состояния несущей системы станка выполнялось в соответствии со следующим алгоритмом: формулирование допущения, построение геометрической виртуальной модели в Solid Works, импортирование модели в СAE систему Workbench (ANSYS), назначение исходных параметров модели, выполнение расчета.

При моделировании определялись контактные деформации в стыках траверсы и стоек портала, стоек и основания портала, наиболее подверженных деформации. Направляющие, приводы подач и привод главного движения для упрощения были заменены близкими по форме и размерам телами. Силовая нагрузка была приложена к шпинделю станка и к заготовке. Для тестового расчета выбрали следующие условия резания: резание производится концевой фрезой диаметром 5мм, заготовка – алюминиевый сплав Д16, глубина врезания 1 мм, направление подачи вдоль оси «X», величина подачи 150 мм/мин, частота вращения шпинделя 2000 мин-1. На рис. 3 показана виртуальная геометрическая модель, построенная в CAD системе Solid Works 10.

Рис. 2. Портальный фрезерный станок

В ANSYS были заданы основные параметры модели и ее расчета: выбран типа решаемой задачи – статический расчет, создана сетка конечных элементов (элементы типа «Тетраэдр») (рис. 4а), причем в местах интересующих неподвижных стыков было произведено загущение сетки (риc. 4,б), выбраны свойства материалов, каждой детали присвоен свой материал (в частности, для статического анализа основания и портала принят алюминиевый сплав Д16Т), после выбора материалов выполнена настройка свойств контактов, отражающих реальные свойства данной сборной конструкции, элементы которой, контактируя между собой, перемещаются друг относительно друга под действием сил и деформируют друг друга.

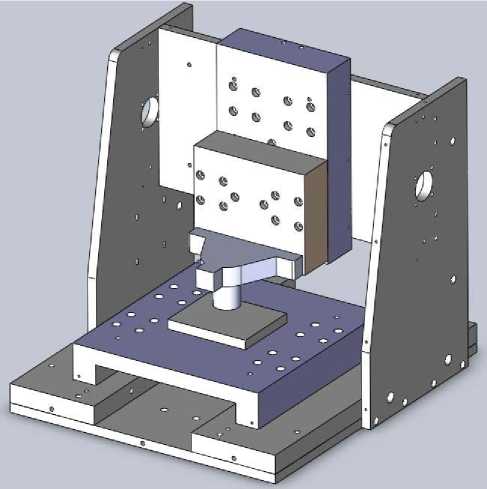
Рис. 3. Виртуальная геометрическая модель станка

При этом в сборке контактируют твердые тела и при импортировании и чтении сборок препроцессором с учетом этого автоматически создаются контакты между деталями, контакт «поверхность-поверхность» (Surface-to-surface) разрешает неэквивалентные сетки на поверхностях контактирующих тел, расстояние автоматического поиска контакта задается параметром Tolerance (допуск) в окне настроек раздела «Contact», значение устанавливается бегунком, в каждой области контакта выделяется контактная поверхность (contact) и целевая поверхность (target), контактная поверхность составлена из элементов типа «contact», целевая – из элементов типа «target»; существует ограничение на проникновение контактной поверхности в целевую: точки интегрирования на контактных поверхностях определяются глубиной проникновения контактной поверхности в целевую; имеет место именно симметричный контакт, т.к. материал элементов системы один и тот же и при возникновении напряжений в стыке, обе его части деформируются в той или иной степени (если в контактной области одна поверхность проявляет свойства контактной (жесткая), а другая – целевой (пластичная), то контакт называют асимметричным, если каждая поверхность является и контактной и целевой одновременно (одинаковая жесткость), контакт называют симметричным).

Закрепление модели станка выполнено по всей площади основания станины. Нагружение модели выполнено силами, приложенными к шпинделю и к заготовке, равными по значению, но противоположными по направлению. На рис. 5 показаны результаты расчета деформированного состояния стыков. Следует отметить, что наибольшая величина контактных деформаций ожидалась в направлении оси «Х», поэтому частные расчеты производились именно в этом направлении.

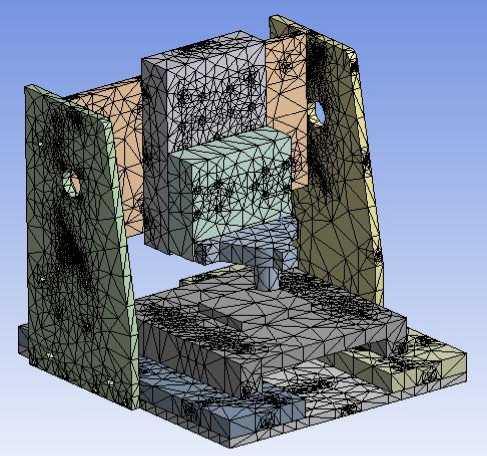
а)

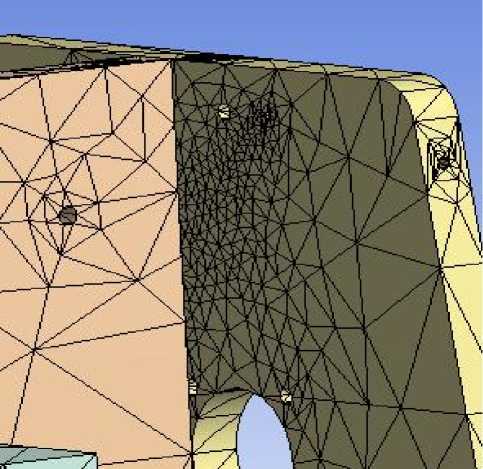
б)

Рис. 4. Сетка конечных элементов несущей системы станка; a – равномерная сетка, б – за- гущение сетки в месте неподвижного стыка

В результате расчета получили: максимальная величина контактных деформаций в стыках стоек портала с траверсой составляет 0,0914 мм (рис. 6), максимальная величина контактных деформаций в стыках стоек портала с основанием составляет 0,0012 мм (рис. 7), в месте стыка деталей с меньшей площадью деформация неравномерна, это объясняется тем, что нагрузка приложена не непосредственно к деталям неподвижных соединений, а именно к шпинделю и заготовке, т.е. усилие передается, пройдя цепочку из элементов станка, несколько раз меняя свое значение и направление. Видно, что рассчитать подобную деформацию более или менее точно вручную – задача весьма сложная и требующая больших временных затрат, максимальное отклонение шпинделя станка от начального (ненагружен-ного) положения составляет 0,208 мм. Увеличение толщины (а, следовательно, и площади контакта) траверсы в 2 раза приводит к отклонению шпинделя 0,09 мм, максимальное значение деформации в месте соединения стойки портала и траверсы составило 0,077мм. Очевидно, что уменьшение отклонения шпинделя вызвано не только уменьшением контактных деформаций, но и повышением жесткости траверсы в целом. Однако такой способ уменьшения контактных деформаций не рационален, более экономически выгодным с точки зрения материалоемкости будет выполнение траверсы с ребрами жесткости.

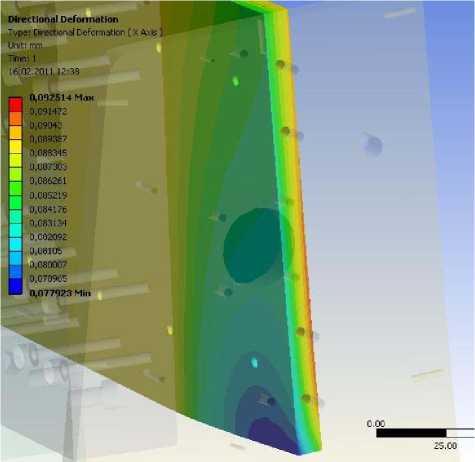
Рис. 5. Максимальная величина контактных деформаций в стыках стоек портала с траверсой

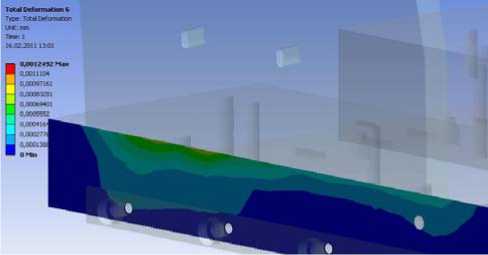
Рис. 6. Максимальная величина контактных деформаций в стыках портала с основанием

Выводы: моделирование позволяет принять конструктивные решения по оптимизации конструкции, кроме того, моделирование деформаций в стыках дает возможность снизить (компенсировать) влияние упругих погрешностей станка на качество изделий.