Моделирование криволинейных поверхностей в задачах газовой динамики

В задачах газодинамики важную роль играет способ задания расчетной области, так как от этого зависит скорость и точность вычислений. Реальные задачи зачастую связаны с обтеканием тел произвольной формы, что делает процесс построения сетки нетривиальной задачей. В этом случае криволинейный контур пересекает расчетную сетку, не совпадая с границами целых ячеек, поэтому для описания начальных условий на границе вводятся дробные ячейки.

Задание граничных условий для тел произвольной формы представляет значительную сложность, поэтому исследования в данном направлении актуальны на сегодняшний день. Так, например, в некоторых работах [1, 2] приводятся расчетные формулы для дробных ячеек, но без постановки граничных условий, за исключением простого случая прямолинейной границы. В других работах [3, 4] вблизи криволинейной границы тела вводится локальная ортогональная система координат, направление осей которой не совпадает с основной прямоугольной системой координат, - такая процедура усложняет алгоритм и вызывает трудности для тел сложной конфигурации.

Подход, используемый в работе [5], не требует введения у поверхности тела какой-либо локальной системы координат, но связан с техническими сложностями построения граничных условий из-за добавления слоя фиктивных ячеек, прилегающих к дробным ячейкам, а также потерей точности при линейной аппроксимации границы тела.

В данной работе рассматривается способ задания начальных условий на границе шара, основанный на нахождении площади ячейки под кривой при помощи интегрирования. Так как для нашей задачи в качестве криволинейной границы выбрана окружность, то не представляет сложности рассчитать площадь, отсекаемую этой окружностью в прямоугольной ячейке. В этом случае существует аналитическое решение для полученного интеграла, чем достигается высокая точность расчетов. Для тела произвольной формы площадь рассчитывается численным интегрированием с кусочно-линейной аппроксимацией криволинейной границы контура.

Механика

Описание алгоритма

Рассмотрим расчетную область, содержащую некоторый сферический объем, на границе которого требуется задать начальные условия (рис. 1). Заштрихованные области вдоль криволинейного контура соответствуют дробным ячейкам. Для наглядности формулы приведены для плос- кого случая.

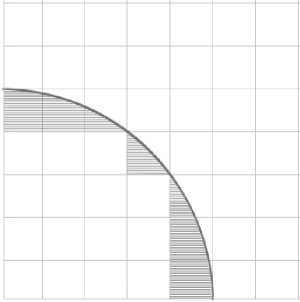
Рис. 1. Схематичное представление сетки с дробными ячейками

Таким образом, если r – радиус окружност и, то интеграл может быть записан в виде

x*   Г 2 2 - x j dx j dy, xiyj

где x_i – горизонтальная координата левой границы ячейки, для которой происходит интегрирование в данный момент, x * может принимать значение либо координаты правой границы ячейки, либо точки пересечения окружности с прямой y j (вертикальная координата сетки); здесь и далее i и j – индексы ячеек, относящиеся к направлениям вдоль x и y соответственно.

При переходе к интегралу по одной переменной имеем j         - yjdx.                                      (2)

xi

После ряда преобразований получим точное решение для интеграла (2).

( x )

Г2    2 г arcsin I I x^r -xV

F (x) = —-— +----yx + C.

Ключевым моментом технической реализации метода является определение пределов интегрирования, так как вариантов пересечения окружности с ячейками сетки может быть несколько – необходимо проработать все возможные типы дробных ячеек, которых в данном случае немного. Далее, подставляя пределы интегрирования для каждой дробной ячейки, находим значение площади по формуле (3).

Параметры на границе тела рассчитываются пропорционально занятой этим телом области в ячейке. Следовательно, найденное значение площади эквивалентно некоторой доле α 1 , занимаемой газодинамическими величинами сферы в данной ячейке, соответственно, (1 – α ₁) приходится на область, граничащую со сферой.

Итак, если плотность и внутренняя энергия в шаре ρ 1 и E 1 , во внешней среде ρ 2 и E 2 , результирующие величины параметров в такой ячейке рассчитываются как

p = axpx + (1 - ax) p2,

E = axPx Ex + (1 - «1) P2E2

P

P = f ( P , E ).

После этапа задания начальных условий на границе тела расчет величин производится по формулам для целых ячеек.

Основные результаты и выводы

Рассмотрим в качестве примера задачу о разлете шара в чистом газе. Пусть в результате взрыва над поверхностью Земли образовался сферический объем сжатого газа, давление внутри объема постоянно. Центр объема находится на оси симметрии Oz цилиндрической системы координат. В начальный момент времени давление внутри шара равно P 1 = 2500·10⁵ Па, в невозмущенной среде P ₂ = 10⁵ Па, плотность ρ ₂ = 1,21 кг/м³. Расчеты проводились методом крупных частиц [6] на сетке размером 330 × 210 узлов.

Моделирование проводилось путем численного решения нестационарной системы уравнений Эйлера, записанной в цилиндрической системе координат. Система законов сохранения и уравнение состояния в безразмерной форме имеют следующий вид:

∂ρr  ∂ρur  ∂ρvr д t     д r     дz’

∂ρur  ∂ρuur  ∂ρuvr д t      д r       дz     д r’

∂ρvr  ∂ρvur  ∂ρvvr д t      д r      дz     дz’

∂ρEr  ∂ρuEr  ∂ρvEr  ∂Pur д t      д r       дz      д r     дz’

P e =

P ( Y - 1)

2 , где u и v – составляющие скорости w вдоль r и z соответственно, e – внутренняя энергия, γ – показатель адиабаты.

Перейдем к результатам расчетов. Представленные на рис. 2 изолинии плотности демонстрируют сохранение сферической формы контактного разрыва с течением времени. Для проверки было выбрано несколько точек на контактном разрыве, их координаты удовлетворяли уравнению окружности, отклонение составило менее 1 %.

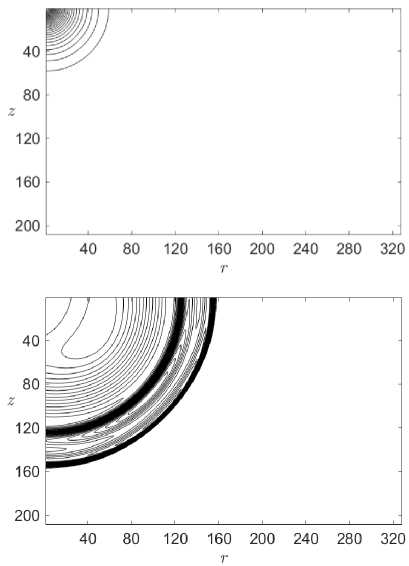
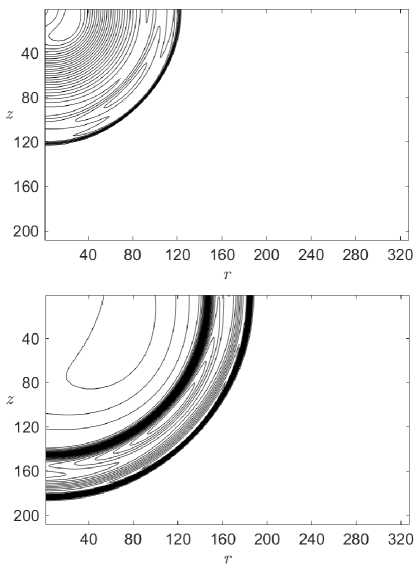
Рис. 2. Изолинии плотности при расширении шара в чистом газе.

Таким образом, введение дробных ячеек позволяет обеспечить сохранение сферической границы в процессе счета.

Механика

Выводы

Результаты расчетов распространения сферических ударных волн, приведенные на рис.и2 позволяют сделать следующие выводы:

• 1.    Задание начальных условий на криволинейной границе с помощью дробных ячеек, в которых физические величины распределены пропорционально занятому телом объему, позволяет наиболее точно описывать расчетную область при решении задач газодинамики.

• 2.    Преимуществами данного метода является его простота и возможность использования дробных ячеек только при задании начальных условий, проводя дальнейшие расчеты по формулам для целых ячеек.

• 3.    Данный подход может быть распространен и на математические модели газовзвеси с химическими превращениями [7].