Моделирование квантованного накопления энергии молекулами, приводящего к его высвечиванию

Вспомним для начала восходящий к детству вопрос о шансах защититься от начинающегося дождика под не очень густой листвой дерева. Для простоты считаем, что несколько (одна-две) первых капель дождя могут удержаться на любом из листочков, образующих «монослой», а падение на него последующей капли опрокидывает листок и все накопленная на нем вода летит вниз на голову. Остается статистически оценить динамику «интегрального выхода» капель воды в такой модели. Действительно, подобные задачи возможны в различных областях.

В области физической химии и спектроскопии нередко встречаются задачи, связанные с накоплением энергии в отдельных молекулах или атомах с последующей передачей этой энергии соседним молекулам или высвечиванием энергии в виде фотона [1]. В частности, накопление энергии с высвечиванием происходит в газовых и твердотельных лазерах и приводит умножению частоты [2]. В простейшем виде это происходит при подаче энергии короткого импульсного лазерного пучка (hv=2,6 эВ) в поток инертного газа, где на выходе получается набор квантов с энергиями N*hv (N = 1 - 80) [3; 4]. Далее, после прохождения монохроматора кванты выделенной энергии используются в экспериментах [5].

Близкое по сути накопление энергии наблюдается при хемилюминесценции синглетного кислорода на поверхности микрокристаллов дифе-нилантрацена [6; 7; 8]. При подлете к поверхности кристалла молекула синглетного кислорода передает свою избыточную энергию (около 1 эВ [9]) молекуле дифенилантрацена. В результате наблюдается высвечивание квантов энергии люминесценции с более чем в 2 раза большей энергией. Для объяснения столь существенного различия между приносимой в одном акте энергией и уносимой энергией была предложена простая модель накопления энергии с последующим высвечиванием энергии [7]. Эта модель рассматривает молекулы дифенилантрацена как отдельные ячейки, которые после накопления определенного числа квантов энергии выделяют всю накопившуюся энергию (квант люминесценции) и возвращаются в основное состояние.

Подобная ситуация проистекает также из физических исследований по хемилюминесценции [3-5]. Хемилюминесценция — это эмиссия света (люминесценция) в результате химической реакции. При этом энергия химической реакции переходит в энергию света и несет информацию о произошедшей химической реакции. В случае поверхностной хемилюминесценции при атмосферных условиях активная частица подлетает к поверхности и передает ей свою энергию, которая после определенного преобразования на активных центрах поверхности высвечивается в виде фотона. В одной из известных реакций взаимодействия возбужденного синглетного кислорода с поверхностью кристаллического 9,10-дифенилантрацена энергия кванта люминесценции дифенилантраце-на более чем в два раза превосходит энергию возбуждения молекулы синглетного кислорода [9]. Учитывая закон сохранения энергии и статистическое распределение тепловой энергии на поверхности кристалла, разумно предположить, что энергия от синглетного кислорода первоначально сохраняется и накапливается в активных зонах (ячейках), а процесс высвечивания происходит только после попадания последующей молекулы синглетного кислорода в активную зону (ячейку).

Построение алгоритма

Обобщая потребности различных приложений с основным упором на хемилюминесценцию, задачу можно описать следующей моделью для излучения при прилипании второй частицы ( r =2) [1; 2; 6].

Сначала предположим, что состояние ячеек становится критическим и дает излучение после подлета к ней для простоты второй ( r= 2) частицы. К ансамблю из к одинаковых ячеек последовательно извне подлетают частицы, каждая ( n ) из которых, случайно встретившись с одной из к ячеек, может «прилипнуть» к этой, ранее свободной ячейке (возбудить ее), либо дать излучение стандартной порции энергии и тем самым вернуть эту ячейку снова в свободное состояние, если она была возбуждена ранее. Требуется статистически оценить динамику вероятности излучения энергии по мере увеличения числа ( n ) частиц, бомбардирующих систему из к ячеек.

Общим для всех подобных процессов является то, что накопление определенного числа бомбардировок какой-либо ячейки оказывается триггером рассматриваемого явления.

Рассмотрим детально процесс установления состояния динамического равновесия модели и оценим его предельные параметры [10]. Для этого предлагаются два этапа программы расчета:

• 1.    Сначала найдем поле (представляющее граф «дерево») чисел « { a i j } » свободных ячеек в виде таблицы с адресами: по вертикали - номер ” n ” прилетающей частицы, по горизонтали - условный номер j состояния; в каждой строке с номером ” n ” имеется 2 ^{n - 1} состояний, например: до прилета первой частицы в нулевой строке имеется одно единственное состояние со всеми к пустыми ячейками: после прилета первой частицы возможно одно единственное состояние с ( к -1) пустыми ячейками к -1; после прилета второй частицы возможно 2 состояния: с к свободными ячейками, если произошло высвечивание - значок «*» (с вероятностью (1/ к ) и с ( к- 2) свободными ячейками, если не произошло высвечивания (с вероятностью ( к -1)/ к ); с прилетом третьей частицы в результате

• 2.    После построения дерева такого поля (таблицы) “ { a i j } ” для каждой строки с номером ” i ” (для выбранного числа ” n ” бомбардирующих частиц) суммируются по выбранной горизонтали вероятности излучения в каждом из состояний ( i,j ). При возвратном подъеме вверх по дереву из каждого такого состояния ( i,j ) учитывается вероятность оказаться в нем. Это делается перемножением вероятностей всех делавшихся переходов при каждом разветвлении в дереве (влево — было излучение, вправо — излучения не было).

переходов из двух состояний с предыдущего уровня ожидаются переходы уже в четыре состояния:

a 3,0 = k - 1 ( Р ₂ ^ з = ( к - 1)/ к ); а 31 = " - 1" ( Р . = 0) ;

а ₃,₂ = к - 1    ( p ₂ ^ ₃ = ( к - 1)/ к ) ; а ₃,₃ = к - 3    ( p ₂ ^ ₃ = ( к - 2)/ к ) .

Здесь а ₃ j = " - 1" ( p ₂ ^ ₃ = 0) означает невозможное состояние.

Далее с прилетом новой частицы на новой « i »-й строке продолжается процесс «размножения» количества состояний (включая невозможные (обозначены значком «х»)) по закону 2 ‘ .

Если излучение происходит при подлете очередной частицы ( n =1,2,3,4,_) к ранее возбужденной ячейке, то графически схему этого процесса можно представить так (рис. 1):

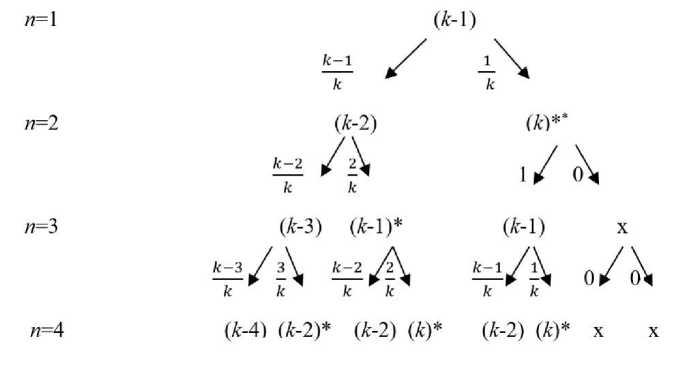
Рис. 1. Схема образования новых состояний при подлете очередных частиц

Здесь в скобках указано число пустых ячеек в соответствующем состоянии системы; возле стрелок, обозначающих последствия подлета n -й частицы, указаны вероятности переходов в новые состояния. В результате излучения, обозначенного значком (*), система переходит в состояние с на единицу большим числом пустых ячеек; если излучения не было, то число пустых ячеек, наоборот, уменьшается на единицу.

Технически поиск адреса предыдущего состояния ( i,j ), из которого попали в данное ( i+1,n ), делается уменьшением ” n ” на единицу и делением второго адреса «j » на два (если высвечивание происходит при подлете к ячейке второй частицы) с взятием целой части. Вопрос о том, какой из переходов (с излучением или без него решается по величине дробной части «j/2 »), либо сравнением соответствующих величин « j» в соседних строках таблицы. После того, как предыдущее состояние определено, учитывается вероятность перехода между «старым» и «новым» состояниями (было излучение или нет).

Результаты

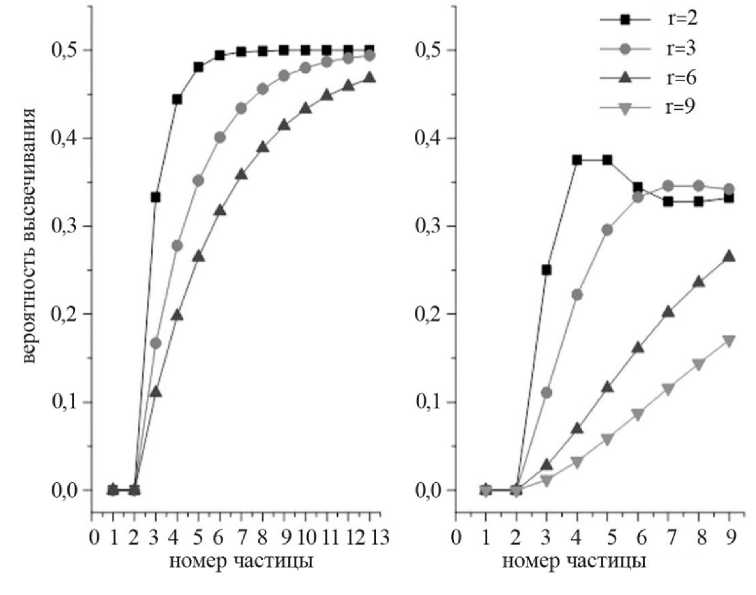
Рис. 2. Расчетные вероятности высвечивания для систем из k= 2 ячеек (слева) и из к=3 ячеек (справа)

Полученные результаты конкретных модельных расчетов имеют общее объяснение в рамках классической теории стационарных случайных процессов.

Если излучение происходит при накоплении в ячейке (пусть сначала единственной) r прилетевших частиц, т. е. при прилете каждой r -й частицы, то при потере номера прилетающей частицы или под длинным их потоком это дает вероятность излучения 1/ r .

Если ячеек в системе много ( k ), то по свойству эргодичности для стационарных случайных процессов усреднение по времени для одной ячейки можно заменить усреднением по (большому) ансамблю из k ячеек с тем же результатом: 1/ r .

Действительно, предельные вероятности на рис. 2 при больших n составляют 1/ r .

То, что вероятность излучения системы приближается к своему предельному значению (0.33) независимо от начальных условий, видно из таблицы 1 для простейшей системы всего из двух ячеек с излучением после попадания в одну из ячеек трех частиц.

Таблица 1

Начальная\Номер ( n ) загрузка \прилетающей ячеек       \ частицы	1	2	3	4	5	6
В обеих ячейках по 2 частицы	1	0.5	0.25	0.25	0.31	0.34
Только в одной ячейке 2 частицы	0.5	0.25	0.25	0.31	0.34	0.34
В обеих ячейках по 1 частице	0	0.5	0.25	0.38	0.31	0.31
Обе ячейки пусты	0	0	0.25	0.38	0.38	0.34

Вероятность излучения системы приближается к своему предельному значению (1/3) независимо от начальных условий (табл. 1 для простейшей системы всего из двух ячеек с излучением после накопления в одной из них трех частиц).

Как показало численное моделирование вероятности излучения после прилета очередной бомбардирующей частицы (отношение числа возможных состояний с излучением к общему числу вариантов состояний 2n), эта величина быстро выходит из режима слабых затухающих колебаний, приближаясь к предельному значению 1/r немонотонно («стационаризуется»).

Выводы

Система выходит на предельное значение вероятности при любых начальных условиях, т. е. переходит в режим динамического равновесия после прилета приблизительно r ≈ k бомбардирующих частиц, причем при некоторых условиях (например: k =2; r =3) этот переходный процесс оказывается немонотонным с затухающими колебаниями.

Последние два обстоятельства не могли быть получены непосредственно из классической теории стационарных случайных процессов и имеют различную информационную природу (ценность):

• 1)    характерная продолжительность процесса «стационаризации», по истечении которой процесс может рассматриваться как случайный стационарный, имеет размерность всей бомбардируемой системы;

• 2)    возможность немонотонного хода процесса «рандомизации», который наблюдается, например, при пороговых (триггерных) значениях ( r =3, 4,…) и малых размерах системы ( k =2) демонстрируется на этой стадии слабыми затухающими колебаниями.