Моделирование логических схем посредством теории множеств

В теории множеств с самопринадлежно-стью [1] была построена адекватная модельная область для лямбда-исчисления [2, 3], а также модель логики высказываний [2]. Кроме того, в семантике самопринадлежности были доказаны теоремы о непротиворечивости лямбда-исчисления [4]. Эти результаты позволяют моделировать посредством теории множеств логические схемы, с обоснованием того, что эти модели непротиворечивы. Ниже описан способ и примеры моделирования логических схем ¹ .

1.    Обоснование моделирования

Теорема о непротиворечивости лямбда-исчисления доказана в слабой (для модельной области лямбда-исчисления) и сильной (на всем М) форме [4]. Для моделирования логических схем значима вторая (сильная) форма теоремы.

Теорема 1 (сильная непротиворечивость). Лямбда-исчисление, реализуемое на теории множеств с самопринадлежностью, – непротиворечиво.

Схема доказательства такова, что "сильное" доказательство непротиворечивости лямбда-исчисления не использует понятия модельной области (т. е. не зависит от результатов теоремы о слабой непротиворечивости). Рассматривается множество всех множеств М. Множества в нём выделяются схемой свёртывания А = {x e M | (x e0 ) или L(x)}. Если высказывание L дополнить лямбда-абстрактором и внешней по отношению к свертыванию переменной, то имеется реализация лямбда-исчисления в теории множеств

А(у) = {x e M | (x e0 ) или L_z(x, Ху.у)}(у), где y e M.

При этом по теореме о непротиворечивости теории множеств [1] высказывание L λ (х, y) не может задавать одновременно множество A(y) и его дополнение, – таким образом, совокупность высказываний L λ (х, y) (для произвольных y из М) – непротиворечива, это и доказывает теорему. □

1 Первоначальные рукописные наброски этой работы относятся к зиме 1996-1997 гг.

Теорема 1 позволяет рассматривать в качестве выражений L(.) с внешней переменной не только произвольные лямбда-выражения, но и выражения, относящиеся к логике высказываний, для которой имеются модели в теории множеств с самопринадлеж-ностью, см. табл. 1, 2.

Таблица 1. Сопоставление элементов теорий [ 2 ]

Элемент теории	Теория множеств	Исчисление высказываний
Константа "невыполнимость"	0	0
Константа "выполнимость"	М	1
Импликация	е	^
Отрицание	(. е 0 )	—1

Таблица 2. Выполнимость [ 2 ]
х	У	х е 0	х е у	((х е 0 ) е 0 )
0	0	М	М	0
0	М	М	М	0
М	0	0	0	М
М	М	0	М	М

Таким образом, наличие констант 0 и М, а также отношений импликации е и отрицания (... е 0 ) позволяет строить модели логических схем посредством теории множеств, причем по теореме 1 модели эти непротиворечивы.

2.    Построения моделей схем

Входы логических схем (см. рис. 1) обозначаются а;, выход - b. Запись модели инвертора такова:

Ь={х е М|(х е0 ) или х=(а е0 )}(а),       (1)

где а ; , b принимают значения 0 , М.

Модель элемента 2ИЛИ:

Ь={х е М|(х е0 ) или х=((а₁ е0 ) е а₂)}(а₁,а₂).

Модель элемента 2И:

Ь={х е М|(х е0 ) или х=((а 1 ё (а 2 е0 )) е0 )}(а_ь а 2 ).

Модель элемента 2И-НЕ:

Ь={х е М|(х е0 ) или х=(а₁ е (а₂ е0 ))}(а₁, а₂).

Эти логические элементы образуют базис, посредством которого строятся остальные более сложные логические схемы [5, с. 12].

В общем виде модель логического элемента - это схема свертывания с высказыванием, дополненная внешними переменными

а ) б)

в ) г )

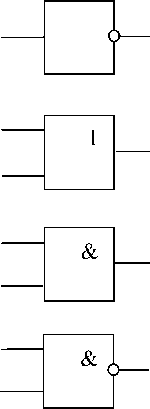
Рис. 1. Элементы логических схем: а) инвертор НЕ, б) элемент 2ИЛИ, в) элемент 2И, г) элемент 2И-НЕ

Ь={х е М|(х е0 ) или L(x, y i ,. у_п)}( y i ,. у_п). (2)

По теореме 1 высказывание L(.) в схеме (2) задает некоторый объект, но не его дополнение. Это означает, что построенные модели логических схем - непротиворечивы.

Аналогично строятся модели более сложных схем, например модель RS-триггера (рис. 2), построенного из двух элементов 2ИЛИ-НЕ.

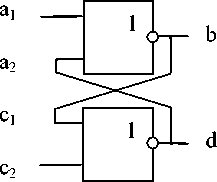
Рис. 2. RS-триггер

Модель RS-триггера состоит из двух взаимосвязанных выражений:

Ь={х е М|(х е0 ) или х=(((а₁ е0 ) е d) е0 )}(a₁, d) d={x е M|(x е0 ) или х=(((с₂ е0 ) е Ь) е0 )}(с₂, b).

Более сложные схемы строятся аналогично, набор основных логических функций, реализуемых в базисе, указанном в табл. 1, приведен в табл. 3.

3.    Замечание о модельной области

В модельной области лямбда-исчисления также строятся непротиворечивые модели, но иного вида, реализующие арифметику на подмножестве множества натуральных чисел, например модель сумматора двух чисел (b=a1+a2) такова:

b={x ∈ M|(x ∈∅ ) или х ∈ P^{a 2} (a 1 )}(a 1 , a 2 ), (3) где a 1 , a 2 ∈ N, а P^{a 2} (a 1 ) – простой последователь степени a 2 , взятый от a 1 .

Известна следующая теорема [4, 6]:

Теорема 2 (слабая непротиворечивость). Лямбда-исчисление над его модельной областью (конечные натуральные числа) в теории множеств с самопринад-лежностью непротиворечиво. □

Общий вид схемы свертывания с высказыванием, дополненной внешними переменными, принимающими значения в конечной области натурального ряда К, К ∈ N, b, у 1 ,… у n ∈ К ∈ N, таков:

b={x ∈ M|(x ∈∅ ) или L(x, у 1 ,… у n )}( у 1 ,… у n ). (4)

По теореме 2 высказывание L(.) в схеме (4) задает некоторый объект, но не его дополнение. Это означает, что построенные модели над областью K натуральных чисел непротиворечивы.

Заключение

Показано, что модели логических схем, строящиеся посредством теории множеств с самопринадлежностью, являются непротиворечивыми; приведены примеры построения базисных логических элементов и RS-триггера. Способ построения моделей логических схем использует модель двузначной логики, для которой ранее доказана теорема исключения третьего [2].

Таким образом, непротиворечивость получаемых моделей обоснована посредством

Таблица 3. Логические функции в базисе модели

Логич. функция	Выражение в базисе	Значения переменных
x	x	∅	∅	M	M
y	y	∅	M	∅	M
не x	(x ∈∅ )	M	M	∅	∅
не у	(у ∈∅ )	М	∅	М	∅
x ⇒ y	(x ∈ y)	M	M	∅	M
х или у	((х ∈∅ ) ∈ у)	∅	М	М	М
х и у	[(х ∈ (у ∈∅ )) ∈∅ ]	∅	∅	∅	М
х = у	([(х ∈ у) ∈ ((у ∈ х) ∈∅ )] ∈∅ )	М	∅	∅	М
х ≠ у	[(х ∈ у) ∈ ((у ∈ х) ∈∅ )]	∅	M	M	∅

результатов теории множеств с самопринад-лежностью.