Моделирование магнитострикционных деформаций в мягких магнитных эластомерах

Обсуждается природа магнитострикции мягкого магнитного эластомера – удлинение/сжатие образца при намагничивании однородным магнитным полем в отсутствие механической нагрузки. Качественный анализ свидетельствует, что внешнее поле оказывает на среду двоякое действие, причем один из механизмов стрикции проявляется на макроскопическом масштабе, а другой – на мезоскопическом. При этом последний, структурный, механизм магнитострикции существенно зависит от особенностей ближнего порядка пространственного расположения магнитных частиц в эластомерной матрице. В доказательство этого утверждения выполнено численное моделирование поведения систем магнитных частиц в упругом двумерном массиве при намагничивании. Показано, что именно наличие/отсутствие многочастичных кластеров приводит к разнице и в знаке, и в величине магнитострикции у материалов, в остальном одинаковых по составу.

MODELING OF MAGNETOSTRICTIVE STRAININ SOFT MAGNETIC ELASTOMERS

Yu.L. Raikher and O.V. Stolbov

Institute of Continuous Media Mechanics UB RAS, Perm, 614013, Russia

The origin of magnetic striction of a soft magnetic elastomer, i.e., its elongation/contraction under an applied uniform magnetic field in the absence of mechanical load is considered. Qualitative analysis shows that the external field has a two-fold effect on the medium. One of the mechanisms manifests itself at the macroscopic level, while the other – at the mesoscopic one. The latter, structural, magnetostriction mechanism depends crucially on the details of the short-range order of the magnetic particle spatial distribution in the elastomer matrix. To prove this conclusion, numerical modeling of the behavior of two-dimensional assemblies of magnetic particles embedded in an elastic layer is carried out. It is shown that it is indeed the presence/absence of multi-particle clusters which causes the difference in both the sign and the magnitude of magnetostriction in otherwise identical materials.

1.    Природа магнитострикции в мягких магнитных эластомерах

Функциональные материалы, получаемые диспергированием малых магнитных частиц в полимерах, хорошо известны [1]. Выбирая в качестве матрицы резину (модуль упругости G ~ 10–100 МПа), этим способом, в зависимости от типа частиц наполнителя, получают как магнитные сердечники или экраны, так и постоянные магниты, способные, не разрушаясь, деформироваться гораздо сильнее металлов и керамик. Системы, где высокодисперсный магнитный наполнитель помещен в очень мягкий ( G ~ 10–100 кПа) полимер, появились сравнительно недавно [2, 3] и сразу вызвали большой интерес. Эти композиты образовали новое семейство смарт-материалов и приобрели известность под названием магнитореологических или мягких магнитных эластомеров (ММЭ). Подходящими матрицами для ММЭ являются полимерные гели и слабо сшитые каучуки, а наполнителями — микро- и нанопорошки железа и ферритов (магнетит, маггемит) [2–8].

Главное, что отличает ММЭ от их жестких аналогов, — это масштаб деформационного отклика на приложенное магнитное поле, в чем легко убедиться, сделав несколько простых оценок. Пусть в нашем распоряжении имеется однородное магнитное поле H напряженностью H ~ 10⁵ А/м, или, в неоднородном случае, перепад поля Δ H ~ H на длине l ~ 1 см; указанный диапазон легко достижим в лабораторных условиях. Примем, что намагниченность ММЭ в таком поле составляет M ~ 10⁴ А/м (в реальности она может быть в разы выше). Вызываемая приложением однородного поля H деформация Δ l / l — её принято называть магнитострикционным эффектом [9] — определяется из баланса магнитного и упругого вкладов в плотность энергии: µ ₀ M ²~ G ( Δ l / l )². Отсюда, полагая модуль сдвиговой упругости материала G ~ 10 кПа, находим Δ l / l ~ 10% , что на несколько порядков превосходит магнитострикционную деформацию любого твердого ферромагнетика.

В неоднородном поле ММЭ деформируется под действием объемных магнитных сил. Приравнивая их работу по смещению элемента на расстояние Δ l приращению плотности упругой энергии, находим Δ l / l ~ µ ₀ M Δ H / G ; подстановка сюда числовых значений снова дает Δ l / l ~ 10%. Видно, что даже умеренное поле вызывает существенное формоизменение ММЭ. Именно эта особенность и позволяет выделить их в отдельный класс материалов, отличный от традиционных магнитных эластомеров (резин).

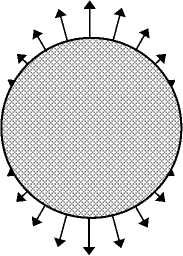
Сделанные оценки соответствуют представлению об ММЭ как о сплошной изотропной упругой среде, любой элемент которой обладает также способностью изотропно намагничиваться. Вероятно, самый известный пример использования этой простой модели — расчет деформации сферы из ММЭ при намагничивании однородным полем [3, 10–12]. Континуальная теория позволяет легко ответить на вопрос о знаке деформации (см. рисунок 1, а ). Поскольку магнитное поле внутри сферы однородно, его силовое действие сводится к растягивающему давлению, которое максимально на «полюсах» — в точках, где вектор H , проходящий через центр сферы, пересекает ее поверхность. Отсюда следует, что при намагничивании сфера растягивается в направлении приложенного поля.

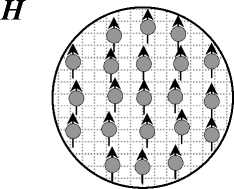
Рассмотрим эту же задачу в мезоскопической постановке; к этому есть все основания, поскольку любой реальный ММЭ является гетерогенным материалом. Рисунок 1, б представляет сферу как дисперсию частиц магнетика в упругой матрице. Приложенное магнитное поле, никак не влияя на матрицу, намагничивает частицы в направлении H (пренебрежем для простоты поправками на внутреннее поле) и создает между ними диполь-дипольные силы. В результате каждая частица притягивается

а

б

Рис. 1. К обсуждению природы магнитострикционного эффекта в ММЭ: а – континуальная модель (стрелки показывают распределение давления); б – мезоскопическая модель (стрелками обозначены магнитные моменты частиц)

к своим соседям по линии вдоль H и отталкивается от таковых по линии перпендикулярной H . При прочной связи частиц с матрицей эти внутренние силы сжимают сферу в направлении поля. Отметим, что это рассуждение и его иллюстрация совершенно аналогичны комментарию, которым сопровождается рисунок 1 b в работе [13].

Возникшее противоречие между сделанными предсказаниями, конечно, не означает, что одна из точек зрения — континуальная либо дискретная — неверна и должна быть отброшена. Несоответствие выводов лишь указывает на чрезмерные упрощения, допущенные при рассмотрении ситуации. Принципиально дело заключается в том, что даже в случае однородного внешнего поля (при отсутствии объемных сил) — намагничивание ММЭ оказывает на его деформацию двоякое действие, в то время как рисунки 1, а и 1, б иллюстрируют каждый из аспектов проблемы в отдельности.

Первый механизм деформирования обусловлен возникновением в образце ММЭ макроскопической намагниченности M . Она создает внутри и вокруг тела собственное поле H _d , масштабом изменения которого является размер образца; внутри последнего поле H d называется полем размагничивания. Взаимодействие между M и H _d определяет ту часть магнитостатической энергии, которая зависит от формы тела. Стремление этого вклада к минимуму реализуется через удлинение тела в направлении поля; для малых деформаций сферы задача имеет точное решение [10], случаи конечных деформаций сферы и эллипсоида изучены численно [11].

Как следует из приведенных рассуждений, тенденция к удлинению при намагничивании присуща только пространственно ограниченным телам, так как в них H d * 0. С учетом этого обстоятельства рассмотренный механизм деформации ММЭ можно назвать магнитострикцией формы . Поскольку поле H _d имеет макроскопический масштаб и практически не зависит от деталей пространственного распределения частиц в матрице, то для качественного объяснения и количественного описания магнитострикции формы вполне подходит континуальная модель. Отметим, что для обычных (твердых) магнетиков деформация, связанная с эффектом формы, ничтожно мала, и ею всегда пренебрегают. Таким образом, значительная величина магнитострикции формы — это специфическое свойство мягких магнитных материалов.

Определение другого магнитодеформационного эффекта — в принятом контексте его следует назвать структурной магнитострикцией — напротив, может быть фактически без изменений заимствовано из физики твердых ферромагнетиков. Магнитострикция этого типа задается взаимодействием частиц на расстояниях меньше или порядка мезоскопического масштаба l = ( N / V ) ^{- 1/3} , где N — число частиц в образце, а V — его объем. Соответствующий вклад в магнитостатическую энергию слабо чувствителен к форме тела и не обращается в нуль в бесконечном массиве материала. С другой стороны, из-за анизотропного характера магнитодипольного взаимодействия эта энергия существенно зависит от того, каков ближний порядок в магнитной подсистеме, от наличия и типа пространственных флуктуаций плотности числа частиц. Отсюда следует, что, в отличие от всегда положительной магнитострикции формы, структурная магнитострикция может иметь любой знак. Поэтому рисунок 1, б — почти правильная решетка частиц, где магнитострикция в пренебрежении эффектом формы получается отрицательной, должен рассматриваться лишь как иллюстративный пример.

Важная роль ближних межчастичных взаимодействий в ММЭ отмечена в ряде работ [13–17]. Однако в целом в современной литературе по магнитомеханике феррогелей и ММЭ четкое разделение вкладов формы образца и его внутренней структуры в магнитострикцию отсутствует. Так, например, даже в основополагающих работах как по эксперименту [2, 9, 18], так и по теории [19, 20] магнитострикцией называется любое формоизменение тела при намагничивании однородным полем.

К этому есть и сугубо практические основания, поскольку в эксперименте разделение двух вкладов в магнитострикцию ММЭ существенно затруднено. В самом деле, легко измерить макроскопические намагниченность и деформацию реального ММЭ, но чрезвычайно сложно «запрограммировать» перед полимеризацией матрицы пространственную структуру ансамбля микрочастиц или провести достоверный морфологический анализ уже изготовленного материала.

В настоящей работе проблема магнитострикции изучается на математической модели, представляющей ММЭ как дисперсию частиц магнитомягкого ферромагнетика в изотропно упругой матрице. Числовая концентрация частиц — они предполагаются идентичными по размеру сферами — близка к той, что имеется в реальных высоконаполненных материалах, планируемых для практического использования. Из-за ограниченности вычислительных ресурсов общее количество частиц берется не слишком большим, и в модельном образце ММЭ (квадрат) они размещаются в один слой. По этой причине полученные результаты не могут претендовать на количественную точность. Однако качественные выводы о поведении ММЭ, которые позволяет получить использованная модель, выглядят вполне заслуживающими доверия.

Главные вопросы, на которые должна отвечать теория магнитодеформационного отклика ММЭ, заключаются в следующем: (1) будет ли заданный образец изменять свои размеры при намагничивании и (2) как ориентированы главные оси возникающего удлинения/сжатия относительно направления приложенного однородного магнитного поля? Выполненные расчеты показали, что для образца ММЭ заданных размеров при заданной средней концентрации частиц структурная магнитострикция существенно зависит от наличия пространственных межчастичных корреляций и может как усиливать, так и ослаблять эффект формы, вплоть до смены знака общей деформации. Определяющим фактором здесь является соотношение между численностями изолированных частиц и частиц, агрегированных в цепочечные кластеры, причем влияние цепочек на общую деформацию тем значительнее, чем больше их длина. Этот факт свидетельствует о том, что для магнитострикции ММЭ чрезвычайно важны одномерные межчастичные корреляции высокого порядка.

2.    Мезоскопическая модель. Численное решение

Модель ММЭ, используемая для расчетов, представляет собой монослой, содержащий 160 идентичных магнитомягких частиц, размещенных внутри плоского квадрата из изотропно-упругого материала; между матрицей и наполнителем имеется полная адгезия. Две смежные границы образца закреплены, две другие свободны (см. рисунок 2). Однородное поле H 0 приложено вдоль оси y , намагниченность частиц подчиняется линейному закону. Магнитодипольная сила, действующая на любую частицу, вычисляется как сумма вкладов всех остальных частиц системы; возникающие при этом механические деформации предполагаются малыми.

• 2.1.    Алгоритм генерации распределения частиц

Поскольку достоверные литературные данные о морфологии реальных ММЭ отсутствуют, то для расчетов используется набор модельных реализаций (в данном случае — 30), в каждой из которых начальное распределение частиц создается путем их случайного размещения в образце. Выбор системы координат задачи и пример реализации иллюстрирует рисунок 2.

Каждая конфигурация такого типа строится по следующим правилам. На основе требуемого значения числовой плотности и в предположении, что частицы идентичны,

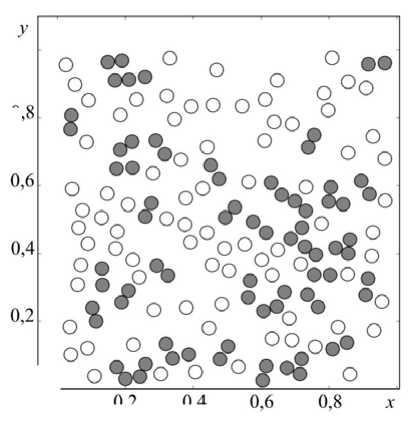
Рис. 2. Система координат и пример случайного распределения 160 частиц в образце квадратной формы; радиус каждой частицы a = 0,02; на смежных сторонах квадрата ( x = 1 и y = 0) смещения по нормали запрещены, см. условия (5). Цветом показан результат кластерного анализа:

светлые частицы – «свободные», темные – входящие в состав кластеров, см. раздел 3

задаются линейные размеры образца и радиус частицы a . Внутри образца с помощью генератора случайных чисел определяются координаты первых N точек, удовлетворяющих условию | r i - r _y | <  2 a, ^i * j, где r i — радиус-вектор i -й частицы в системе координат рисунка 2. Эта операция дает положения центров частиц в получаемом «экземпляре» реализации. Частицы размещаются в указанных точках образца, после чего начинается расчет его магнитодеформационного поведения.

• 2.2.    Уравнения равновесия матрицы

Для изучения механических свойств ММЭ используется модель, в которой реальный гетерогенный материал заменяется континуумом с кусочно-постоянными упругими свойствами. А именно, рассматривается плоский слой мягкого материала (матрица) с N круговыми лакунами диаметром 2 a , в каждую из которых без зазора помещен круг того же диаметра из жесткого материала (частица). Расчет изменения формы образца при намагничивании ведется в приближении малых деформаций и в предположении, что для обоих компонентов системы справедлив закон Гука.

В принятой модели уравнение равновесия образца и условие несжимаемости материала принимают вид:

V o f mag = 0,

J 1 ( e ) = 0.

Здесь о — тензор напряжений Коши; J 1 — первый инвариант тензора малых деформаций e ; f _mag — плотность магнитных сил.

Закон Гука для несжимаемого материала записывается в форме о = - p g + 2 Ge .

В этой формуле: p — гидростатическое давление; g — единичный тензор; G — модуль сдвига. Как указано выше, в рассматриваемом случае G — кусочно-постоянная функция, зависящая от координат; для полимерной матрицы её значение принимается равным единице, а для магнитных частиц (металл или феррит) — G = 105. Таким образом, зададим модуль сдвига выражением:

G ( r ) = £ { 10 5 I i ( r ) + [ I i ( r ) - 1 ] } , i

в котором I_i ( r ) — функция-индикатор, равная единице, когда радиус-вектор r принадлежит i -й частице, и нулю в противном случае. Для тензора деформации принимается стандартное кинематическое соотношение

e = 2 (vu + V uT),

где u — вектор перемещений, а индекс T означает транспонирование матрицы. На двух смежных сторонах образца ( x = 1 и у = 0) предполагается неразрывный контакт ММЭ со стенками

u = 1 = 0, u y\y = 0 = 0,

но допускается свободное скольжение вдоль них. Две другие смежные стороны считаются свободными:

n - al    = 0, n • al , = 0,

I x = 0                             l y = 1

где n — вектор наружной нормали. Принятая постановка задачи автоматически обеспечивает сплошность образца, то есть отсутствие полостей на всех границах раздела частица/матрица.

2.3. Магнитные силы

В приближении малых деформаций задачи расчета упругих напряжений и магнитных сил разделяются. Сначала в предположении, что диполи точечные, находятся парные магнитодипольные силы, которые действуют между частицами в исходной конфигурации. Энергия точечного магнитного диполя имеет вид:

U ⁽ i ) = - ц ⁽ i ) • H i ) ;

здесь ц ⁽ i ) — магнитный момент данной i -й частицы, а H ^{( 1} ) — вектор локального магнитного поля, определяемый как сумма внешнего однородного поля H 0 и полей от всех остальных диполей в точке, где находится i -я частица:

Л

H ( Г ) = H 0 + Z

, = 1 j ^ i ^L

-«Г+

3( ц ^{( , )} ■ > ;, ■)

r ⁵

Г ij

Г = F. — Г r j r i r j .

Далее предполагается, что магнитный момент ц ^{( 1} ) сферической магнитомягкой частицы всегда направлен вдоль внешнего поля H 0 и равен

Ц

3 v H

3 х^{- 1} + 4 п ,

где v — объем, ах — объемная магнитная восприимчивость материала частицы. Для сильно намагничивающихся веществ (например, для железа, у которого х>>10 ³ ) формула (9) сводится к известному предельному выражению ц = 3 v H 0 / 4п .

Сила, приложенная к i- й частице, находится как градиент ее дипольной энергии:

NN

F=-V£и„’=ц<'’.^ - j=1

j * ij