Моделирование механизма снижения плотности минерализации эмали в окрестности вершины Фиссуры

Основная функция зубочелюстной системы заключается в пережёвывании пищи, выполнение которой возможно благодаря особой анатомической форме зубов жевательной группы, а именно моляров и премоляров. Элементы окклюзионной поверхности ежедневно испытывают значительные нагрузки при функциональных жевательных движениях. Хрупкость и высокая подверженность механическим повреждениям эмали представляют серьезную опасность при расклинивании пищей фиссур – клиновидных ( V -образных) выемок, формирующихся в глубине борозд зуба в результате срастания долей коронок. Глубокая фиссура часто образуется в результате неполного срастания долей бугорковой эмали в развивающихся зубах и может доходить почти до дентиноэмалевой границы. Фиссуры подразделяют на центральные (срединные), проходящие через всю окклюзионную поверхность, и дополнительные (радиальные),

пересекающие центральную поверхность в лингвальном или вестибулярном направлении [3; 5].

Исследования геометрии окклюзионной поверхности зубов получили развитие, начиная с работ [12; 14]. В более поздней работе [13] была проведена классификация видов износа окклюзионной поверхности, в то время как в [15] было выполнено клиническое in vivo исследование анатомии моляров и премоляров двухсот пациентов с установлением корреляции между глубиной центральных ямок и подверженности элементов окклюзионной поверхности к разрушению. В [9] была изучена подвижность элементов окклюзионной поверхности зубов, а в [29] использовался метод конечных элементов (МКЭ) для численного исследования распространения напряжений на контакте поверхности жевательных бугров. МКЭ использовался также в [19] для исследования горизонтальной составляющей силы надавливания, вызывающей изгиб жевательного бугра, и расклинивания,

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

приводящего к значительному растяжению в области центральной ямки. В статье [17] рассмотрены механизмы взаимодействия пищи и окклюзионной поверхности зуба человека. Работа [26] посвящена анализу характера разрушения эмали в вершинах фиссур 126 интактных премоляров человека. Математическое моделирование процесса разрушения эмали в вершине фиссуры зуба проведено в работах [27; 28]. В исследовании [20] предложен подход к расчету предела прочности керамической коронки зуба с использованием МКЭ. Работы [31; 32] посвящены исследованию процесса распространения трещин в керамических зубных коронках и в окрестностях фиссур с использованием расширенного МКЭ. В [11] был экспериментально воссоздан процесс расклинивания фиссуры пищей путем нагружения её боковых граней индентором. В статье [6] проведено исследование поведения цельнокерамических элементов зубных протезов при квазистатических механических испытаниях с непрерывной регистрацией сигналов акустической эмиссии. В работе [4] проведено исследование напряженно-деформированного состояния (НДС) элементов протезной конструкции при функциональных нагрузках с использованием МКЭ.

В стоматологической практике на поверхности эмали в вершинах фиссур может происходить накопление кариесогенных бактерий (в первую очередь групп Streptococcus mutans и Lactobacillus ), что ведет к локальному снижению pH , деминерализации эмали, развитию кариеса и снижению механических свойств ткани [1; 2; 24; 25]. Появление трещины в вершине фиссуры приводит к синдрому треснувшего зуба, при этом трещина возникает либо в продольном направлении по фиссуре вглубь зуба, либо отсекает один из жевательных бугров [18, 21]. Если трещина пересекает дентиноэмалевую границу, происходит обнажение дентинных трубочек [7; 22; 23], содержащих окончания нервных волокон [10; 16], что приводит к болевым ощущениям пациента при надавливании на зуб [8].

Подводя итоги краткого обзора современного состояния исследований, можно сделать вывод, что наиболее уязвимым элементом окклюзионной поверхности эмали с точки зрения прочности эмали коронки являются фиссуры, изломы которых являются естественными концентраторами напряжений эмали. Концентрация напряжений эмали в окрестности вершины фиссур во время их расклинивания продуктами питания в процессе пережёвывания пищи создаёт условие для понижения плотности минерализации эмали и повышает риски возникновения кариеса. Для оценки возможности возникновения вышеуказанных рисков следует осуществить математическое моделирование фиссуры для анализа напряженно-деформированного состояния (НДС) эмали в окрестности вершины фиссуры. С этой целью строится аналитическое решение залачи о НДС эмали с V-образной выемкой в виде развернутого клина. Новизна работы состоит в том, что сила прикуса моделируется путем задания распределенных по отрезкам на гранях фиссуры сил, ортогональных граням, и сил, действующих вдоль граней, препятствующих проникновению пищи вглубь фиссуру.

Моделирование фиссуры и схема её расклинивания

Эмаль фиссуры моделируется развернутым клином AA 'MOLA "A с углом раствора MOL =360° - ф , представленным на рис. 1, боковые стороны которого имитируют геометрию межбугоркового пространства фиссуры. Фиссура образована радиус-векторами, проведенными из вершины фиссуры - точки O - по касательным к поверхности бугров, её образующих, в точках E и F . Угол EOF =2φ в вершине клина характеризует раствор фиссуры. Элемент пищи схематично представляется в виде круглого жёсткого диска с центром в точке O' , который под действием силы прикуса Q опирается на боковые грани фиссуры в окрестности точек E и F . Обозначив расстояния EF=b, EO=FO=a , угол φ определяется формулой arcsin( b/2a ).

Для определения НДС эмали и степени концентрации напряжений в окрестности вершины фиссуры точки О рассматривается задача о раскрытии бесконечного упругого клина AAMOLA'A с углом раствора 2а=360 °-2ф из эмали круглым жёстким диском, имитирующим пищу, с центром в точке О ' под действием силы прикуса Q , коллинеарной биссектрисе OO '. Диск передает воздействие силы Q на грани OM и OL в виде распределённых по отрезку [ c,d ] сил /( r ) , ортогональных OM и OL , и распределённых сил g(r) , действующих вдоль граней OM и OL , препятствующих проникновению пищи глубже в фиссуру. Описанная нагрузка на клин AA MOLA "A симметрична относительно оси симметрии OO' - биссектрисы угла MOL . Действие распределённых сил /( r ) и g(r) приводит к возникновению НДС в клине AA'MOLA'A с

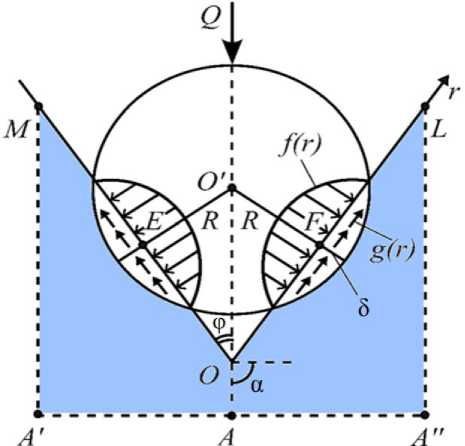
Рис. 1. Схема нагружения упругого клина AA'MOLA"A, имитирующего фиссуру концентрацией в вершине клина O . Решение поставленной задачи состоит в определении НДС эмали в окрестности вершины фиссуры точки O и степени концентрации напряжений стгr, ст6 в, ст,^ при приближении к этой точке изнутри эмали, где стгг, ств6 - нормальные, а σ – касательные напряжения в эмали зуба.

НДС бесконечного клина AA'MOLA"A в условиях плоской деформации описывается дифференциальными уравнениями теории упругости в напряжениях [30].

^д ° rr Д ^д ° r e , ° rr ^- ° ее д r   r д е       r

+ Р F r = 0,

в котором Q является силой прикуса (см. рис. 1). На Рисунке 2 введены следующие обозначения:

b = R^e (2 - e) , e = §R-1, где δ – наибольшее заглубление диска в боковую поверхность фиссуры (FC), e – относительное заглубление диска, b - полуширина параболы f (r), cF=Fd, a – расстояние от середины (c, d) до точки O, OF. Реализация дополнительных условий на f (r) вида (5), (6) приводит к формулам для τ и σ где σ , σ , σ – напряжения в полярной системе координат (r,е) с центром в точке O,F^ - массовые

b ^{2 ,  0}4 b ^.

силы.

Граничные условия на боковых гранях клина

В результате этого f (r) принимает вид

е = ± а представляются равенствами

f(r) = 3 P [1 -(r-a)2 2 c < r < d , v ’   4 b        b2

где h ( r ) = H ( r - c ) - H ( r - d ) , 0 <  c <  d , где H ( r ) -

функция Хевисайда. За счет симметрии задачи

граничные условия можно задать на одной грани клина

где c = a - b , d = a + b

Из естественного условия a - b >  0 следует ограничение на угол p раствора фиссуры

0 < p <  arctg

Считается, что при неограниченном возрастании

1 - e

v V e(2 - e) >

n

r ( r ^^,|е| < а )   напряжения   с_гг,с_вв,с_гв в клине

AA'MOLA"A исчезают. Для получения конечного результата решения задачи – распределения НДС в окрестности вершины фиссуры в виде напряжений ст_гг, с_вв, ст^ - необходима конкретизация функций f ( r ) и g ( r ) в граничных условиях (3), так как функции f ( r ) и g ( r ) должны описывать распределенные усилия,

Функция g (r) , характеризующая трение между диском O’ и боковой стороной фиссуры, определяется законом Амонтона – Кулона

передаваемые жёстким диском с центром O' (рис. 2), на боковую поверхность фиссуры OL . Исходя из опыта решения контактных задач, функцию f ( r ) -

вертикальное распределения усилия (напряжения) – можно аппроксимировать параболой следующего вида

параметры τ , σ которой определяются из дополнительных на f ( r ) условий

f (a ± b ) = 0,                (5)

a + b

J f (r)dr = P.                 (6)

a - b

Суммарное усилие P , создаваемое функцией f ( r ) , получается после выполнения условий статики

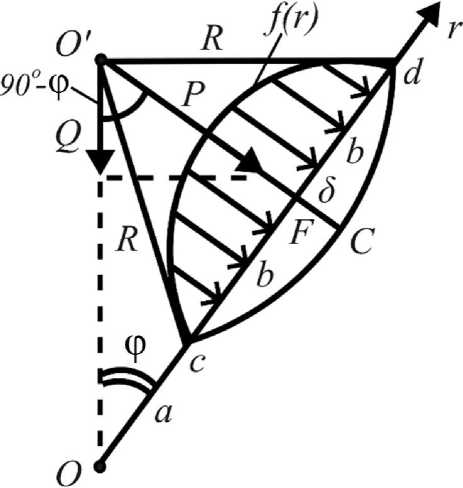
Рис. 2. Схема нагружения боковой поверхности параболой f (r)

P cos ( 90 °-ф ) = 2 ^{- 1} Q ,            ( 7 )

g ( ^r ) = k ( ^r ) '

где k – коэффициент трения между пищей в виде диска и боковой поверхностью фиссуры.

Решение задачи для клина

, A d ² u 9          A du 9 Z A/ 2 л du 9 a

(к-1) —r--2(p + к)——+ (к + 1) p2 -1 —r- = 0, (     ) d92     (P ) d9 (     )(/^     ) d9’ d u           dudu

( к + 1 )--- 9 - 2 ( p -к ) — ^r- + ( к- 1 ) p ² - 1 —2_ = 0,

(     ) d92     (      ) d9   (     )(

Основными неизвестными поставленной задачи об определении НДС клина AA'MOLA"A из эмали при его раскрытии распределенными усилиями f ( r ) и g ( r ) , r e [ c , d ] , являются смещения u_r , u₆ и напряжения σ , σ , σ . Для их определения, кроме

использования уравнений равновесия клина

воспользуемся соотношениями закона Гука

связывающих напряжения с деформациями

(1), [30],

^G rr

2 G

1 - 2 v

f_x d u_r ( 1 -v) —-

(^{V     7} d r

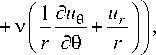
2 G

^G 99 = ,  ,

1 - 2 v

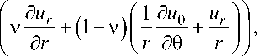
^G r 9

f 1 d u_r   d u ₉   u ₉ )

= G 1 .

( r 59   d r   r J

Подставив соотношения (12) в уравнения равновесия (1), в отсутствие массовых сил Fr = Fe = 0, получим уравнения равновесия упругого клина (|0| < а, 0 < r < го)

в смещениях

Яр ,          . <

— + ( 1 ^{- 2 v} ) l A u r d r            I

u r ^{2 d u} 9 L A

= 01

r ² r ² 59 J

где к = 3 - 4 v , а штрихи над u 9 означают производные по 9 .

Для установления связи между трансформантами смещений u 9_е ( p , 9 ) и трансформантами напряжений □9г ее r9 ( p , ® ) воспользуемся соотношениями закона Гука (12). С этой целью каждое из соотношений (12) умножается на r ^p с последующим интегрированием по r от 0 до го. Введя обозначения для трансформант напряжений

□9у(p,9) = jc5y(r, 9) rpdr      19| < a, где 5у обозначает поочередно rr, 00, r0 , получим равенства

9     2 G / /     x     X 9

=" = 1 - 2 ?P p ⁺ 1 ) " p ) u ^{9 +v} J '

т« = ?|9 (1 -(p+i)v)u9+(i-v)du^ ,

^J f du9)

G9 = G dur- - 1 + p u91

r 9     ( d 9   (

---+ (1 - 2 v) A u_A r 59  ⁽       ) (    ⁹

^u 9

r ²

г d u r )=o. r ² 59 J

Общее решение системы обыкновенных дифференциальных уравнений (15) в случае симметрии задачи по 9 записывается в виде

5ur , ur , 5uQ„ где g = —r- + —r- +--9  - объёмная деформация, dr   rr a d2    1 5  ,  1  52_

A = —- +----+ — —- - оператор Лапласа.

5 r ²   r 5 r  r ² 59 ²

u r: ( p , 9 ) = A 1 ( p + k ) cos ( p +1 ) 9 +

+ A 2 ⁽ p ^- 1 ) cos ⁽ p ^{- 1 )9} '

u 9 ( p , 9 ) = A 1 ( p - k ) sin ( p +1 ) 9 +

+ A ₂ ( p -1 ) sin ( p -1 ) 9,

Для решения поставленной задачи (1), (3) об определении НДС клина AA'MOLA"A применяется интегральное преобразование Меллина. Для реализации метода каждое из уравнений (1) умножается на rp+1 и интегрируется по r от 0 до го , при этом вводятся обозначения для трансформант смещений го u 9( p, 9) = Juy( r, 9) rp-1 dr    19|

где γ обозначает либо r, либо θ .

В результате получим обыкновенные дифференциальные уравнения равновесия упругой среды относи тельно трансформант смещений u9, u9 (6) вида

где  Ak = Ak (p) , k = 1,2 являются постоянными, которые определяются из граничных условий.

В предположении, что интегралы Меллина от функций f (r) и g (r) существуют в обычном смысле, граничные условия (3) после применения преобразования Меллина переходят в граничные условия для соответствующих трансформант

d

• ⁹ = ^{a  G}Q9 (p^{, a}) = ^-f⁹(p)^,f⁹(p) = Jf (^r ) ^rp^dr,

^c                (19)

d

• ^g99(p^{, a}) = g⁹(p)^,g⁹(p) = Jg (^r ) ^rp^dr.

c

Подставив соотношения (18) в равенства (17), получим соотношения

< (p, 9) = —2Gp x x [(p + 3) A1cos (p +1)9 + (p — 1) A2 cos (p —1)9] ^99 ( p , 9) = 2 Gp ( p — 1)x x [A cos (p +1)9 + A cos (p —1)9]

° H)( p, ⁹) = ^—2Gp^x

x[(p +1) A1 sin(p +1)9+ (p — 1) A₂ sin(p —1)9].

Постоянные Ak = Ak (p), к = 1,2 определяются из граничных условий для трансформант (19) после подстановки в (19) соотношений (20). В результате этого получается система линейных алгебраических уравнений относительно A, к = 1,2:

2Gp (p — 1) [ A1 cos (p +1)9 + A₂ cos (p — 1)9] =

—

_r, ,    . , =^—f^{Г( p}),   ,     .  .            (21)

2Gp[(p +1) A1 sin(p +1)9+ (p — 1) A₂ sin(p —1)9] =

=ge(p), решение которой имеет вид

A1 = ^(—f^e( p)^sin(p^—1)^{a —}

^—g^e( p)^cos(P ^—1)^a)(^{2 GR} (p)) 1.

A2 = ⁽g^Г( p )( p^—1) ^cos( p⁺1)^{a +}

+f^e( p)(p +1) sin (p + 1)a) ■

■( 2 G (p — 1) R (p))^-1.

R (p) = sin (2ap) + psin (2a).

Подстановкой A и A из (14) в определяются трансформанты смещений напряжений   ст-,   °ee,   °Ге ■ После

иГ ,

и (20)

и Г  и

обращения

трансформант смещений иГ и ug с помощью формул обратного преобразования Меллина получим иy(r, 9) =     UyГ(p, 9) r pdp,

2n i

Г

19| < a, 0 < r <«,

где у обозначает r и 9. Формулы для смещений упругой среды ur (r, 9) и ue (r, 9) записываются в виде контурных квадратур обратного преобразования Меллина (23), где контур Г совпадает с мнимой осью комплексной плоскости переменной интегрирования p и,(r,9) = -— [H2^ (1

^{4 G П}i¹  Ru ( p ) I ^r

| p f^e( p) dp +

1   HH—(p, 9)1 1 A^p

+----- ----F^l - I g^e (p)dp.

^{4 GП}i I Ru ( p ) I r J

Нижний символ у обозначает О или r .

Подынтегральные функции в (24) даются формулами

H+ =—(p + k) cos (p +1)9 sin (p — 1)a +

+ (p +1) cos (p — 1)9 sin (p +1) a;

H— =( p — 1) cos (p —1)9 cos (p + 1)a —

— (p + k) cos (p +1)9 cos (p — 1)a;             (25)

H+ =—(p — k) sin (p —1)9 sin (p — 1)a +

+ (p +1) sin (p — 1)9 sin (p + 1)a;

H9 =( p — 1) sin (p —1)9 cos (p + 1)a — — (p — k) sin (p —1)9 cos (p — 1) a;

Ru (p ) = p (sin2 p a + p sin2a),            (26)

в которых к дана после формулы (15).

Формулы для напряжений о„. gg ,g (r,О) получаются с помощью обратного преобразования Меллина в форме

°5у(^r, ⁹) = ^ J°Sy(p,⁹) ^rp¹dp, Г

19| < a,0 < r < да, где 5у обозначает поочередно rr, 99, r9 . После подста новки ст^ формулы (27) записываются в виде контурных квадратур обратного преобразования Меллина с контуром Г, описанным после (23)

°5_Y⁽r,⁹⁾=^—^1-J L5Y(_fp,⁹) l¹1 f^e(p)dp+

2П nJ ^R°(p) V ^r J

^Г                              (28)

1   _fL5_Y( p, 9)l 1A ^p

⁺^r~J       i г I g^e(p) dp,

2nri^L Ra( p ) V r J в которых подынтегральные функции даются формулами

L+_r =—4sin (1 — p )a cos (1 + p )9 +1 (1 — p ,1 + p ) —

—l (1 + p,1 — p), l (и, v ) = и sin и a cos v9, L^r = 2cos (1 — p )a cos (1 + p )9 + n (1 + p ,1 — p) +

+n (1 — p,1 + p), n (и, v) = и cos va cos и9, L99= l (1 + p ,1 — p) — l (1 — p ,1 + p),           (29)

L99 = ^—( p^—1)( m (1 ^—p ,1 ⁺p ) ^—m (1 ⁺p^{,1 —}p )), m (и, v) = cos и a cos v9,

L+9 = —( p + 1)( h (1— p ,1+ p ) + h (1+ p ,1— p )), h (и, v) = sin и a sin v9,

Lr9 = g (1⁺p ,1^—p ) ^—g (1^—p ,1⁺p ), g (^u,^v ) = = и cos va sin и9,

R°( p )=R (p),               (30)

где R (p) дана в (22).

Исследования подынтегральных функций в (24), (28) показали, что они являются функциями p и на беско- нечности при:

Ip\ ^*, n< I arg (p )|<ⁿ .

Нормальны напряжения σ , МПа

a

Нормальные напряжения σ , МПа б

Нормальные напряжения σ , МПа

в

Рис. 3. Области равновеликих напряжений σ в окрестности вершин фиссур с углами раствора

2ф = 60°( а) ,80° ( б) ,100°( в)

Значения полюса p₀и показателя степени y₀ = p₀+1 в формулах (33)

Ф	89,5°	84°	78,5°	78°	67,5°	62°	56,5°	51°	45,5°
P 0	-0,989011	-0,882438	-0,797285	-0,728745	-0,673583	-0,629430	-0,594437	-0,567093	-0,546115
Y 0	0,010989	0,117562	0,202715	0,271255	0,326417	0,370570	0,405563	0,432907	0,453885
Ф	40,0°	34,5°	29°	23,5°	18,0°	12,5°	7,0°	45,5°	0°
P 0	-0,530396	-0,518970	-0,510993	-0,505727	-0,502590	-0,500837	-0,500146	-0,500001	-0,500000
Y 0	0,469604	0,481030	0,489007	0,494273	0,497471	0,499163	0,499854	0,499999	0,5

H±(p, 9) R- (p) = O (p-1), 4( p, 9) R-1 (p ) = O (1),

Y <> r, 9,

y3 <> rr, 99, r 9,

комплексной плоскости. После преобразований формула для смещений (24) приобретает вид

при этом интегралы в (24), (28) существуют в обычном смысле.

Для численной реализации полученных формул для u , u и σ ,σ ,σ необходимо в повторных интегралах (24) и (28) поменять порядок интегрирования , учитывая, что внешний материал берётся по контуру в

1      ”

u Y( r, 9) = "t; Re^

G   k = 1

H + ( p_t , 9 ) a + b R . '( p . )   .^Jb

pk

I d ^ +

”

+1 ReV

G £

H - ( p_k , 9 ) ^{a +}+ b ^R /( p > ) a^j Ь

pk

I d ^ ,       (32)

0 < 9 < a,0 < r < a + b ,

в которых двукратный полюс p= 0 отбрасывается из физических ограничений, P k ( k = 1,2,... ) - полюсы подынтегральных функций или нули функции R ( p ) за исключением устранимых особых точек, a, b определены в (9), f ( ^ ) , g ( ^ ) даны в (9), (11) соответственно. Формула для o_gY ( r ,0 ) принимает следующий вид

°5У

a + b

(r, 9) = -J a - b

f (1) L+y( P o,6) fl) p 0+1 1    Ra ' ( P 0 ) I r J

+

k =1

L 6y ^{( p} k , ⁹⁾ R . ' ( P k )

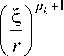
d 1 +

₊a r b g C l ) L-A p o , ⁹ ) fl) ^p °⁺* - J    ^{1    R} a ' ^{( p} 0 ) I ^{r J}

k =1

L 6y ^{( p} k , ⁹⁾ R . ' ( p k )

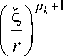
y5 <>  rr, 99 , r 9 ,0 < 9 < a ,0 <  r <  a + b, где p – полюса подынтегральных функций или нули функции R _c ( p ) , за исключением устранимых особых точек. Формула (33) показывает, что напряжения имеют при r = 0 особенности по r порядка у₀ = p ₀ +1, т.е. r ~^Yo (при r ^ 0 ). В таблице приведены значения первого слева от начала координат полюса p и показателя степени γ в формулах (33) для различных полууглов раствора фиссуры φ.

Расчёты напряженности в окрестности вершины фиссуры

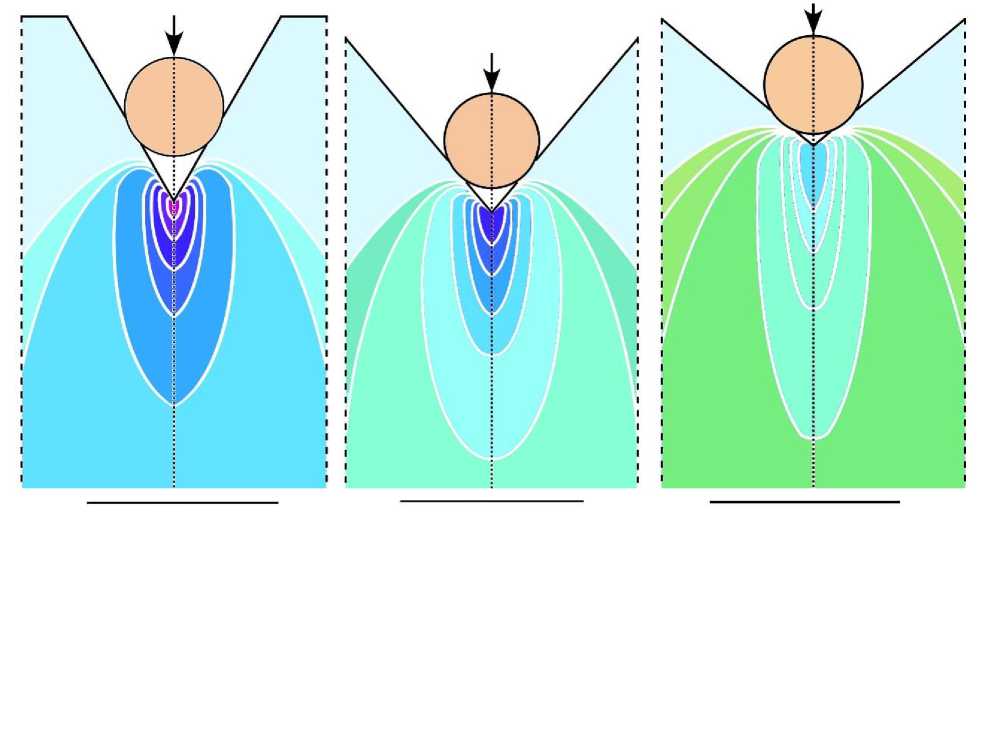
Полученные формулы (32), (33) дают возможность изучить НДС в окрестности вершины фиссуры. Напряжения σ θθ , рассчитанные по формулам (33) в окрестности вершины фиссуры, представлены на рис. 3 для трёх различных углов раствора 2φ=60°, 80°, 100° вместе с

Заключение

В настоящей работе в ходе построения аналитического решения задачи о НДС эмали с V -образной выемкой в виде развернутого клина получены формулы для исследования степени концентрации напряжений в окрестности вершины фиссуры зуба человека. Математическое моделирование силы прикуса проведено путем задания распределенных по отрезкам на гранях фиссуры сил, ортогональных граням. Теоретические исследования, проведенные по изучению окклюзионной поверхности моляров и премоляров показывают, что фиссуры с меньшими углами раствора с большей вероятностью могут спровоцировать возникновение кариеса при одной и той же силе прикуса, отсюда следует вывод: при изготовлении искусственных коронок необходимо избегать создания фиссур с малыми углами раствора. Процесс дробления и перетирания пищи приводит к существенным механическим воздействиям на окклюзионную поверхность моляров и премоляров. При этом математическое моделирование продемонстрировало возникновение существенного механического напряжения, приводящее со временем к снижению плотности её минерализации и риску возникновения кариеса в эмали коронки зуба.

• 1.    Беляев А.Ю., Гилева О.С., Муравьева М.А., Свистков А.Л., Скачков А.П. Исследование механических свойств здоровой и поврежденной кариесом зубной эмали с помощью микроиндентирования // Российский журнал биомеханики. – 2012, № 3. – С. 57-64.

• 2.    Левицкая А.Д., Сюткина Е.С., Гилева О.С., Галкин С.В., Ефимов А.А., Савицкий Я.В. Оценка микроструктуры и минеральной плотности очага искусственного кариеса эмали по данным рентгеновской компьютерной микротомографии // Российский журнал биомеханики. – 2018. – Т. 22, № 4. – С. 485-502.

• 3.    Линченко И.В., Стекольникова Н.В., Машков А.В., Пчелин И.Ю., Буянов Е.А. Современные методы изучения биометрических характеристик окклюзионной поверхности боковых зубов // Фундаментальные исследования. – 2014. – Т. 10, № 7 – С. 1346–1350.

• 4.    Олесова В.Н., Бронштейн Д.А., Лернер А.Я., Олесов Е.Е., Бобер С.А., Узунян Н.А. Напряженно-деформированное состояние в протезной конструкции на дентальном имплантате при цементной фиксации искусственной коронки // Российский журнал биомеханики. – 2016. – Т. 20, № 4. – С. 311-315.

• 5.    Петрикас А.Ж., Смирнова М.А., Баженов Д.В., Эхте А.А., Петрикас О.А. Частная анатомия зубов в рисунках и цифрах: учеб. пособие. – Тверь: Тверская государственная медицинская академия, 2013. – 45 с.

• 6.    Рогожников А.Г., Вильдеман В.Э., Биккулова А.В., Зубова Е.М., Рогожников Г.И., Шулятникова, О.А. Экспериментальное    исследование    процессов    разрушения

  полунатурных керамических элементов зубных протезов методом регистрации сигналов акустической эмиссии // Российский журнал биомеханики. – 2018. – Т. 22, № 2. – С. 230-240.

• 7.    Садырин Е.В., Ёгина Д.В., Волков С.С., Айзикович С.М. Оценка плотности и микрогеометрических характеристик пломб из стеклоиономерного цемента и композитного материала:  биомеханическое ex vivo исследование

  // Российский журнал биомеханики. – 2022. – Т. 26, № 2. – С. 67-73.

• 8.    Симановская Е.Ю., Еловикова А.Н., Тверье В.М., Няшин Ю.И. Биомеханическое описание особенностей функций жевательного аппарата у человека в норме и при различных патологических процессах // Российский журнал биомеханики. – 2004, № 4. – С. 15-26.

• 9.    Borcic J. Anic, I., Smojver I., Catic A., Miletic I., Ribaric S.P. 3D finite element model and cervical lesion formation in normal occlusion and in malocclusion // Journal of oral rehabilitation. – 2005. – Vol. 32, № 7. – P. 504-510.

• 10.    Carda C., Peydro A. Ultrastructural patterns of human dentinal tubules, odontoblasts processes and nerve fibres // Tissue and Cell. – 2006. – Vol. 38, № 2. – P. 141-150.

• 11.    Constantino P.J., Bush, M.B., Barani, A., Lawn, B.R. On the evolutionary advantage of multi-cusped teeth // Journal of The Royal Society Interface. – 2016. – Vol. 13, № 121. – P. 20160374.

• 12.    Crompton A.W., Parker P. Evolution of the mammalian masticatory apparatus: the fossil record shows how mammals evolved both complex chewing mechanisms and an effective middle ear, two structures that distinguish them from reptiles // American Scientist. – 1978. – Vol. 66 – № 2 – P. 192–201.

• 13.    Dahl B.Ö.R.L., Carlsson G.E., Ekfeldt A. Occlusal wear of teeth and restorative materials: a review of classification, etiology, mechanisms of wear, and some aspects of restorative procedures // Acta Odontologica Scandinavica. – 1993. – Vol. 51, № 5. – P. 299-311.

• 14.    Kay R.F. The functional adaptations of primate molar teeth // American journal of physical anthropology. – 1975. – Vol. 43, № 2. – P. 195-215.

• 15.    Lagouvardos P., Sourai P., Douvitsas G. Coronal fractures in posterior teeth // Oper Dent. – 1989. – Vol. 14, № 1. – P. 28-32.

• 16.    Longridge N.N., Youngson C.C. Dental pain: dentine sensitivity, hypersensitivity and cracked tooth syndrome // Primary dental journal. – 2019. – Vol. 8, № 1. – P. 44-51.

• 17.    Lucas P.W., Peters C.R., Arrandale S.R. Seed‐breaking forces exerted by orangutans with their teeth in captivity and a new technique for estimating forces produced in the wild // American Journal of Physical Anthropology. – 1994. – Vol. 94, № 3. – P. 365-378.

• 18.    Lynch C.D., McConnell R.J. The cracked tooth syndrome // Journal-Canadian Dental Association. – 2002. – Vol. 68, № 8. – P. 470-475.

• 19.    Magne P., Belser U.C. Porcelain versus composite inlays/on lays: effects of mechanical loads on stress distribution, adhesion, and crown flexure // International Journal of Periodontics & Restorative Dentistry. – 2003. – Vol. 23, № 6.

• 20.    Pegorin F., Kotousov, A., Berto, F., Swain, M.V., Sornsuwan, T. Strain energy density approach for failure evaluation of occlusal loaded ceramic tooth crowns // Theoretical and applied fracture mechanics. – 2012. – Vol. 58, № 1. – P. 44-50.

• 21.    Saatwika L., Prakash V., Malarvizhi D., Subbiya A.A Review on Cracked Tooth Syndrome // Indian Journal of Forensic Medicine & Toxicology. – 2020. – Vol. 14, № 4. – P. 1119-1122.

• 22.    Sadyrin E.V. Correlating the Mechanical Properties to the Mineral Density of Brown Spot Lesion in Dentine Using Nanoindentation and X-ray Micro-tomography // Advanced Materials Modelling for Mechanical, Medical and Biological Applications. – Springer, Cham, 2022. – P. 389–398.

• 23.    Sadyrin E.V., Mitrin B.I., Yogina D.V., Swain M.V. Preliminary study of distribution of mechanical properties and mineral density by depth of liquid saturated carious dentine // IOP Conference Series: Materials Science and Engineering. – IOP Publishing, 2021. – Vol. 1029, № 1. – P. 012056.

• 24.    Sadyrin E.V., Yogina D.V., Swain M.V., Maksyukov S.Y., Vasiliev A.S. Efficacy of dental materials in terms of apparent mineral density restoration: Composite resin, glass ionomer cement and infiltrant // Composites Part C: Open Access. – 2021. – Vol. 6. – P. 100192.

• 25.    Sadyrin E., Swain M., Mitrin B., Rzhepakovsky I., Nikolaev A., Irkha V., Yogina D., Lyanguzov N., Maksyukov S., Aizikovich S. Characterization of enamel and dentine about a white spot lesion: mechanical properties, mineral density, microstructure and molecular composition // Nanomaterials. – 2020. – Vol. 10, № 9. – P. 1889.

• 26.    Salis S.G., Hood, J.A., Stokes, A.N., Kirk, E.E. Patterns of indirect fracture in intact and restored human premolar teeth // Dental Traumatology. – 1987. – Vol. 3, № 1. – P. 10-14.

• 27.    Sornsuwan T., Ellakwa A., Swain M.V. Occlusal geometrical considerations in all-ceramic pre-molar crown failure testing // Dental Materials. – 2011. – Vol. 27, № 11. – P. 1127-1134.

• 28.    Sornsuwan T., Swain M.V. Influence of occlusal geometry on ceramic crown fracture; role of cusp angle and fissure radius // Journal of the mechanical behavior of biomedical materials. – 2011. – Vol. 4, № 7. – P. 1057-1066.

• 29.    Spears I.R., Crompton R.H. The mechanical significance of the occlusal geometry of great ape molars in food breakdown // Journal of Human Evolution. – 1996. – Vol. 31, № 6. – P. 517-535.

• 30.    Timoshenko S., Goodyear J.N. Theory of Elasticity. – New York: Mc Graw-Hill Book Company Inc., 1970. – 608 P.

• 31.    Wan B., Shahmoradi M., Zhang Z., Shibata Y., Sarrafpour B., Swain M., Li Q. Modelling of stress distribution and fracture in dental occlusal fissures // Scientific reports. – 2019. – Vol. 9, № 1. – P. 1-10.

• 32.    Zhang Y., Mai, Z., Barani, A., Bush, M., Lawn, B.

Fracture-resistant  monolithic  dental crowns  // Dental

Materials. – 2016. – Vol. 32, № 3. – P. 442-449.

Финансирование. Работа выполнена при финансовой поддержке РНФ, грант № 22-19-00732.

Благодарность. Автор благодарит руководителя РЦКП НОЦ «Материалы» Зеленцова В.Б. (Донской государственный технический университет, г. Ростов-на-Дону) и профессора Свэйна М.В. (Сиднейский университет, г. Сидней, Австралия) за помощь в постановке задачи, а также Бардакову Р.A. (Донской государственный технический университет, г. Ростов-на-Дону) за помощь в проведении численного исследования.