Моделирование механизмов рыночного регулирования спроса

• 1.    Введение

• 2.    Структурно-функциональная модель информационно-экономического механизма регулирования потребности в специалистах

  В условиях нестабильности социально-экономического развития задача определения основных параметров рынка труда на перспективу является довольно сложной, и применительно к региональному уровню еще не найдено достаточно универсальных методов ее решения. В то же время с помощью существующего математического аппарата и статистических методик прогнозирование локального рынка труда может иметь решение ( Корчак , 1996).

Процессы, происходящие на рынке труда, являются ключевыми для любой рыночной экономики. В современной России происходит качественная смена типов и форм занятости, стремительно возрастает сегментация рынка труда по различным признакам, в том числе и по территориальному. Состояние рынков труда неразрывно связано с реализацией экономической и социальной функций региона. В разных частях России эти функции реализуются различным образом и крайне неравномерно. Это ведет к росту межрегиональной и внутрирегиональной дифференциации рынков труда, что актуализирует вопросы прогнозирования потребности в трудовых ресурсах.

Многоаспектность проблемы получения надежного прогноза в таком случае, с очевидностью, требует системного подхода и одного из его инструментов – структурно-функционального моделирования, состоящего в тщательном анализе системы, что обусловливает получение возможного оптимального решения (рис. 1).

Нормативы

Статистика

Основные задачи

Демография

Экономика

Информационно-экономический механизм регулирования потребности в специалистах

Прогнозы

Сценарии

Рекомендации ►

Алгоритмы

Среда реализации

Рис. 1. Структурно-функциональная модель информационно-экономического механизма регулирования потребности в специалистах

Исходная информационно-нормативная база включает в себя ряд блоков показателей по структуре экономики, занятости и системе профессионального образования; норм, нормативов, налогов, сборов, платежей, а также демографических, социальных и других показателей, характеризующих масштабы безработицы, в том числе среди специалистов по специальностям. Все эти показатели, нормы и нормативы используются для прогнозирования спроса (потребности) на специалистов; оценки федерального бюджета, бюджета региона и на этой основе – для формирования бюджетов вузов; моделирования занятости и численности высвобождаемых работников, в том числе специалистов; прогнозирования размеров и структуры приема в вузы ( Прогноз потребности …, 2000; Прогнозирование развития …, 1999; Мурманская область …, 2001).

К основным показателям (базовым и прогнозным), используемым в моделировании, можно отнести следующие:

• 1)    Экономические показатели: структура экономики в отраслевом разрезе по стоимостным показателям (в абсолютном и относительном измерении – %, разрезы); предполагаемые структурные сдвиги в тех же разрезах; индекс валового внутреннего продукта (всего и в отраслевом разрезе); индекс валового национального продукта (всего и в отраслевом разрезе); индекс производительности труда; индекс фондовооруженности; индекс капитальных вложений; прибыль по народному хозяйству; индекс

уровня жизни населения; индекс прожиточного минимума (отношение стоимости "набора" либо "корзины" к средней заработной плате (доходу); масштабы деятельности (в различных разрезах) негосударственного сектора (в том числе малого предпринимательства).

• 2)    Демографические показатели: баланс трудовых ресурсов России в отраслевом разрезе (в среднегодовом исчислении); демографический прогноз в разрезе возрастных групп; размеры миграционного движения в части молодежной группы населения; баланс распределения молодежи по видам (уровням) профессионального образования.

• 3)    Показатели занятости населения: численность и структура занятости в отраслевом разрезе; размеры и структура высвобождения работников (в отраслевом, профессиональном и возрастном разрезе); численность и структура занятых специалистов (в отраслевом разрезе); численность занятых специалистов (в профессионально-квалификационном разрезе); масштабы высвобождения специалистов; нормативы численности специалистов в социальной сфере (врачей на 10 тыс. чел. населения, учащихся на одного преподавателя и т.п.) и в сфере сервиса в целом.

• 4)    Показатели намерений населения относительно получения образования и выбора вида деятельности: конкурс при поступлении в высшие и средние профессиональные учебные заведения (в разрезе профессиональных групп учебных заведений и специальностей); намерения потенциальных абитуриентов (учащихся старших классов школ); намерения выпускников высших и средних профессиональных учебных заведений относительно выбора вида деятельности (совпадение или несовпадение предварительного выбора с фактическим).

Формирование как исходной информационно-нормативной базы, так и прогноза развития экономики должно проводиться с учетом необходимости реализации мер по стабилизации социально-экономического положения; социальной поддержке населения и сдерживанию безработицы; созданию благоприятного инвестиционного климата; формированию условий и потенциала будущего экономического роста, перехода от распределительной к инвестиционной стадии приватизации и эффективному управлению государственным имуществом; сокращению взаимной задолженности и разрешению кризиса платежей; развитию рынка труда, товаров, капиталов, недвижимости и их инфраструктуры; обеспечению государственных нужд; выполнению федеральных и региональных программ.

Системный анализ внешних и внутренних факторов (состояние рынка образовательных услуг на региональном и федеральном уровне, динамика макро- и микроэкономических процессов на региональном и федеральном уровне, демографические процессы) дополняется количественными оценками с использованием методов математического моделирования.

Стоит еще раз заметить, что множественная регрессия, автокорреляционные или адаптивные методы не могут дать корректных результатов в рассматриваемом случае ввиду следующих причин:

• -    отсутствует достаточный объем исторических данных;

• -    наличие переходных процессов в экономике и социальной сфере;

• -    сложность в учете временных лагов между отдельными явлениями;

• -    ограниченность сценарного анализа динамики основных показателей.

• 3.    Моделирование динамики спроса на специалистов

Ввиду этих обстоятельств необходимо использовать модели, явным образом учитывающие и отражающие взаимосвязь различных процессов во времени, т.е. динамические модели. Нами предполагается, что рыночные механизмы настройки системы образования на выпуск необходимого количества специалистов с высшим образованием играют определяющую роль в динамике спроса и предложения ( Федосеев , 1996). Государственные механизмы регулирования будут отражаться в модели посредством учета целевых заказов. Влияние высокой изменчивости внешней среды переходной экономики будет учитываться методами имитационного моделирования ( Шелобаев и др., 1998).

В обобщенном виде динамическую модель можно представить как систему конечно-разностных (или дифференциальных) уравнений вида:

X n+1 = Ф 1 ( X n ; Y n ; Z n ; D nk E);                        Z n+i   = Ф 3 ( X n ; Y_ro Z n ; D nk E);

• ^Yn+1 = ^Ф 2 ⁽ X n ; ^Yn^; Z n ; D n-k^; E;                         D n+1   = ^Ф 4 ^{( X}n^{; Y}n^{; Z}n^; D n-k ; E ^);

где X_n+1 - группа показателей (выпуск, бюджет, доходы, выпуск по специальностям и т.д.), имеющих отношение к системе высшего образования;

Y_n+1 - группа показателей (отраслевая структура, бюджет, доходы, динамика роста, индексы и т.д.), описывающих экономическую среду;

Z_n+1 - группа показателей (структура общества, доходы на душу населения и т.д.), отражающих социально-культурные аспекты региона;

D n-k – группа показателей, характеризующих демографический фон;

E – группа показателей, отражающих влияние других регионов и заграницы;

Ф i – функции, определяемые при построении динамической модели на основе законов предметной области.

Так как сбор всей необходимой информации для постановки задачи в таком виде совершенно нереален, а получаемые уравнения, учитывающие функциональные взаимосвязи, очень сложны для рационального анализа, то искусство моделирования состоит в построении компромиссной модели. Такая модель должна отражать поведение существенных для нашего анализа показателей, иметь простую для анализа структуру, иметь возможность проводить сценарный анализ по принципу "… что, если …".

Поэтому наша модель в качестве основных переменных будет содержать показатели, касающиеся выпуска специалистов и производных от них.

Так как нами предполагается рыночный механизм выработки реального спроса и предложения специалистов, то основным законом предметной области будет служить закон соответствия спроса и предложения. То есть общий спрос в рыночных условиях, сформированный в текущем периоде, индуцирует соответствующее предложение в следующем периоде, что схематично можно представить как уравнение баланса, выполняющееся в среднесрочной перспективе: предложение = спрос.

Предложение в данном контексте есть просто общий выпуск специалистов. Спрос в агрегированном представлении в данной модели разбивается на следующие составляющие (рис. 2): 1) среднесрочная потребность на специалистов в равновесной ситуации;

• 2)    спрос, индуцированный текущей динамикой в изменении выпуска специалистов;

• 3)    спрос на специалистов со стороны государственного сектора (целевые программы);

• 4)    спрос, индуцированный другими регионами и заграницей; 5) спрос, индуцированный демографическими процессами.

  

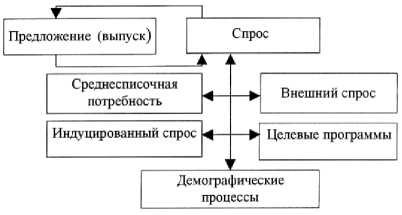
  Рис. 2. Механизм рыночной настройки спроса и предложения на специалистов

  
  

Конкретный      выбор      функциональных зависимостей будет представлен вслед за вводом основных    переменных    модели.    Рассмотрим предварительные соображения, лежащие в основе построения модели. Если основывать свои рассуждения на прямом учетном подходе, то, казалось бы, достаточно на основе региональной статистики оценить количество выпускников школ и молодых людей в пределах определенной возрастной группы (16-20 лет) и скорректировать на долю поступающих в вузы или завершающих обучение.

Однако данный показатель скорее играет роль ресурсной базы и в данном качестве может играть роль естественного ограничения, спрос же фактически определяется экономическими и социальнокультурными потребностями и стереотипами. В то же время при таком подходе сложно учесть потребность в получении второго образования, переквалификации и реальную потребность в специалистах с высшим образованием.

С другой стороны, моделирование взаимозависимой динамики агрегированных показателей позволяет учитывать инвариантные взаимосвязи, складывающиеся на рынках труда и образовательных услуг, и редуцировать к минимуму число определяющих параметров и показателей ( Шелобаев и др ., 1998; Экономико-математические методы …, 1998).

Итак, в модели нами используются следующие переменные:

X t – выпуск специалистов с высшим образованием в t -м году, одновременно, если t – текущий период, то X t+1 – предложение, индуцированное текущим спросом;

C t – среднесрочная потребность на специалистов с высшим образованием в равновесной ситуации в t -м году;

I t – спрос, индуцированный текущей динамикой в изменении выпуска специалистов с высшим образованием в t -м году;

G t – спрос на специалистов со стороны государственного сектора в t -м году;

E t – спрос, индуцированный другими регионами и заграницей в t -м году;

D t – спрос, индуцированный демографическими процессами; и параметры:

a – коэффициент индуцированного спроса (для линейной модели);

b – предельное воспроизводство специалистов;

A – автономный спрос на специалистов;

• p – прирост государственного целевого спроса за год;

• g – относительный прирост внешнего спроса за год.

Для каждой составляющей необходимо определить способ представления через основные показатели и параметры модели. Метод выбора функциональных зависимостей должен оптимальным образом сочетать две противоположные задачи: достаточная полнота описания явлений и возможность последующего количественного анализа. После реализации всей программы построения и анализа модели можно вернуться к вопросу об уточнении или выборе других функциональных зависимостей.

Выбираем основные функциональные зависимости:

для среднесрочной потребности на специалистов с высшим образованием (СВО) используем линейную модель зависимости от текущего выпуска X t :

C t = bX_t + A ;

для спроса, индуцированного текущей динамикой в изменении выпуска СВО в t -м году, используем модель линейного прироста:

I t   = a ( X t - X t-1 );

для спроса на специалистов со стороны государственного сектора в t -м году:

G t = (1 + p ) G t—i ;

для спроса, индуцированного другими регионами и заграницей в t -м году:

E t = (1 + g ) E t—i .

В результате уравнение модели можно представить в виде:

Xt+1 = It + Ct + Gt + Et + Dt или

X +1 = a ( X t - X t — i ) + bX t + A + G t + E t + D t ,

G t = ^{(1 +} P ) G t-1 ,                   E t = ^{(1 +} g ) E t-1 .

Так как модель представляет конечно-разностное уравнение второго порядка, начальных условий требуется два, и в качестве таковых выберем значения X 0 и X 1 в 1995 и 1996 гг. Выбор обоснован требованием устойчивости определения других параметров модели при небольших вариациях исходной информации. Устойчивость - свойство модели иметь решения с относительно небольшим изменением при малых вариациях как в параметрах модели (параметрическая и структурная устойчивость), так и исходных исторических данных (устойчивость по отношению к ошибкам информационной базы и появлению новых данных).

В качестве дополнительных используем начальные условия:

X 0 = X 1995               X 1 = X 1996                 G 0 = G                 E 0 = E

X1995 и X1996 можно использовать из имеющейся региональной статистики, а G и E можно определить при решении обратной задачи из сопоставления фактических и модельных данных. Показатель Dt характеризует влияние демографических процессов на потребности в специалистах с высшим образованием. Способ его нахождения сводится к следующему алгоритму. Вначале полагаем Dt = 0, затем методами оптимизации находим параметры модели (обратная задача). Циклические составляющие отклонений фактических данных и модельного расчета и будут определять Dt.

Для исследования полученных модельных уравнений можно воспользоваться стандартными процедурами решения конечно-разностных линейных неоднородных уравнений 2-й степени. Необходимо вначале решить однородное уравнение ( A + G_t + E_t + D_t = 0) с помощью подстановки

Xt = C* (Л), где Л - характеристическое число уравнения, а C - произвольная константа. В ходе решения характеристического уравнения получаются два корня Л1 и Л2, которые определяют линейную оболочку решений однородного уравнения. Добавление частного решения неоднородного уравнения и определение двух произвольных констант из начальных условий окончательно определит решение. Основная цель подобного анализа - исследование модели в линейном приближении на параметрическую устойчивость.

Области альтернативных портретов поведения траекторий X t в пространстве параметров a и b определяются из решения характеристического уравнения для Л, граница различных областей устойчивости задается в плоскости ( a, b ) уравнением:

( a + b )² - 4 a = 0.

Замкнутое решение для реалистичного вида функций G t , E , D t в общем случае невозможно (как для данного случая, так и в нелинейной модели), и поэтому необходимо использовать численные методы.

Чтобы конкретизировать модель для целей прогнозирования, необходимо по имеющейся статистике о выпусках специалистов по Мурманской области определить соответствующие коэффициенты. Для этого требуется решить обратную задачу динамического моделирования. В данном случае это может быть реализовано посредством нелинейной оптимизации рассогласования модельных решений относительно фактических. Заметим, что коэффициенты индуцированного спроса ( a ), предельного воспроизводства специалистов с высшим образованием ( b ) и автономного спроса на специалистов с высшим образованием ( A ) фактически инкапсулируют в себе зависимость от макроэкономических показателей, показателей социально-культурного окружения и внешней среды.

В данном представлении модели подразумевается, что указанные параметры являются гладкими функциями экономических показателей, отражающими в синтетическом виде влияние окружения на динамику процессов в области образования.

Алгоритм нахождения параметров модели состоит из следующих этапов:

• 1)    используем численную процедуру решения уравнений модели при произвольных параметрах;

• 2)    составляем функцию рассогласования между модельными данными и данными региональной статистики как сумму квадратов рассогласований по годам;

• 3)    решаем задачу минимизации для критерия рассогласования при вариации искомых параметров;

• 4)    повторяем процедуру нахождения параметров для ряда различных объемов исходной информации (анализ устойчивости, чувствительности и возможной тенденции в изменениях).

Для численной оптимизации нами использовался метод сопряженных градиентов.

Для оценки устойчивости параметров процедура оптимизации повторялась пять раз на различной по объему базе. Полученные данные показывают изменения в параметрах модели при выборе различных по объему выборок данных. В частности, по малой величине стандартных отклонений относительно средних значений можно судить об устойчивости модели по отношению к новой информации.

Анализ приведенных данных показывает незначительную изменчивость параметров модели, что можно интерпретировать, как ее устойчивость относительно новой информации.

На основе полученных значений параметров можно рассчитать динамику выпуска специалистов с высшим образованием и, соответственно, дать прогнозные оценки на будущие периоды.

Коэффициент корреляции для данной модели равен 0.98, что говорит о высоком соответствии ретроспективным данным.

Описание реальных отношений между экономическими объектами и производственными процессами наиболее рационально в полной мере осуществляется с помощью моделей имитационного типа, базирующихся на методе Монте-Карло. Имитационная модель экономического процесса по своему смыслу является динамической, поскольку в любом описании такого процесса всегда явно или неявно присутствует время ( Кибиткин , 2000) .

Основным механизмом, позволяющим учитывать обратные связи в системе подготовки специалистов, является равновесие на соответствующих рынках в зависимости от складывающихся предложения, спроса и уровня зарплаты.

В связи с этим нами предложена модель, явно учитывающая спрос на специалистов с высшим образованием в зависимости от заработной платы в следующих выделенных секторах: в коммерческих организациях, в бюджетных организациях, на внешнем рынке.

Если в первом и третьем случаях механизмы формирования спроса и предложения чисто рыночные, то для бюджетных организаций возможны две модели регулирования:

• 1)    программная модель, в которой задается на каждый период времени определенный объем мест для специалистов с высшим образованием;

• 2)    рыночный механизм, аналогичный первому и третьему секторам.

Остановимся на модели с рыночным регулированием спроса во всех трех секторах.

Исходным уравнением модели является следующее:

Xn+1 = a (Xn — Xn-1) + bXn + A +IzZn + IgGn + IeEn + Dn, где Zn - зарплата, складывающаяся в коммерческих организациях (в долях от средней зарплаты по региону); a - коэффициент индуцированного спроса;

• b - предельное воспроизводство специалистов с высшим образованием;

• A - автономный спрос на специалистов с высшим образованием;

G n - зарплата в бюджетных организациях;

E_n - зарплата, предлагаемая внешними экономическими агентами;

D n - спрос, индуцированный демографическими процессами;

I z , I g , I e - коэффициенты, характеризующие прирост выпуска специалистов с высшим образованием при изменении соответствующей оплаты на единицу (коэффициенты чувствительности).

Спрос на специалистов с высшим образованием формируется в зависимости от имеющегося количества специалистов предыдущего периода и складывающейся зарплаты. Это можно записать в виде линейной функции:

Спрос ( бюдж.орг. ) = b x X n .1 + b z Z n , где b x , b z - коэффициенты, характеризующие изменение спроса при изменении соответствующих показателей X и Z и определяются выбранной текущей стратегией бюджетных организаций по расширению (сокращению) специалистов с высшим образованием.

Предложение специалистов с высшим образованием также можно представить в виде линейной функции:

Предложение ( бюдж.орг. ) = i_xX n .1 + i z Z n .

Параметры i_xz аналогичны b_xz , только служат для определения предложения. Однако, если изменения показателей b xz определяются выбором проводимой политики привлечения специалистов с высшим образованием, т.е. являются управляющими параметрами, то значения i xz складываются стихийно на рынке труда.

Изменениями b коммерческие организации фактически либо привлекают, либо отталкивают специалистов с высшим образованием в определенные промежутки времени.

Тогда условие равновесия можно представить в виде уравнений, отражающего соответствие спроса и предложения:

b x X n-1 + b z Z n = i x X n—1 + i z Z n ;                   Z n = X_n- 1 ■ ( b x — i x ) / ( i z — b z ).

Аналогичные уравнения можно записать для сектора бюджетных организаций и, соответственно, для рынка внешних потребителей:

g x X n-1 + g z G n = k x X n-1 + k z G n ;               G n = X n-1 ■ ( g x — k x ) / ( k z — g z );

e x X n-1 + e z E n = I x X n-i + I z E n ;                 E n = X_n_ i ■ ( e x - I x ) / ( I z - e z ).

где g аналогично b , k аналогично i , e аналогично b , l аналогично i.

Для программной модели управления спроса на специалистов в секторе бюджетных организаций соответствующие уравнения баланса спроса и предложения можно представить в виде:

B n = k x X n-1 + k z G n ,

B n = ^{( 1 +} p ) B n-1 ,                                   G n = B n / k z ^- k x / k z----- . X n-1 .

B 0 – задано

В результате получается система уравнений, которая позволяет найти X_n , Z_n , G_n и E_n в зависимости от выбранных параметров модели I , i , b , g , k , e , l , p .

Для определения этих параметров и составления прогнозов необходимо решить обратную задачу - восстановить параметры динамической модели по результатам сопоставления модельных данных с фактическими. Данная задача решается методами нелинейной оптимизации.

Учет случайных факторов осуществляется в рамках имитационного моделирования. Один из соответствующих розыгрышей с использованием генератора случайных чисел, распределенных по нормальному закону со стандартным отклонением, взятым на основе анализа модель .фактных отклонений представлен на рис.3.

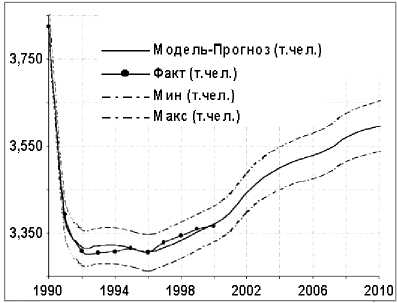
Рис. 3. Динамика изменения показателей спроса на специалистов

Численная реализация динамической модели осуществлена в среде программирования VBA с использованием табличного процессора MS Excel. Созданная программа позволяет моделировать динамику при широком диапазоне исходных данных, имитировать различный уровень изменчивости внешней среды, решать обратные задачи по восстановлению параметров модели на основе методов нелинейной оптимизации, строить различные сценарии как при выборе управленческих воздействий, так и при альтернативных вариантах социально-экономической динамики в стране и регионе.

Имитационная модель позволяет определять, какие возможны последствия при изменении политики привлечения специалистов в различных секторах экономики (т.е. за счет изменения следующих показателей b , g , e ) и может использоваться при разработке политики в области занятости и регулировании рынка труда. Формирование как исходной информационно-нормативной базы, так и прогноза развития экономики должно проводиться с учетом необходимости реализации мер по стабилизации социально-экономического положения, социальной поддержке населения и сдерживанию безработицы. Рыночные механизмы настройки системы образования на выпуск необходимого количества специалистов играют определяющую роль в динамике спроса и предложения. Государственные механизмы регулирования отражаются в модели посредством учета целевых заказов. Использование метода Монте-Карло позволяет учесть влияние высокой изменчивости внешней среды в условиях региональных рыночных отношений.

Особенностью предложенной модели является то, что в ней интегрировано анализируется влияние различных рыночных факторов и выбранных методов управления рынками труда в различных секторах экономики. Если эту модель рассматривать как управленческую, то она позволит определить, какие возможны последствия при изменении политики привлечения специалистов в различных секторах экономики при разных сценариях развития территориальных социально-экономических систем. Разработанная модель может использоваться территориальными исполнительными органами и, при существующей системе, прежде всего, службой занятости .

4. Заключение

Применение имитационного моделирования позволяет прогнозировать ситуацию на региональном рынке труда на основе различных сценариев развития экономики региона. Анализ экспериментальных расчетов, проведенных на основе различных сценариев развития экономики региона, подтверждает целесообразность и возможность применения имитационной модели при разработке региональной политики занятости.