Моделирование минимальных триангулированных поверхностей: оценка погрешности вычисления площади при проектировании сооружений

DOI:

Некоторые задачи, возникающие при проектировании архитектурных сооружений, сводятся к построению поверхностей минимальной площади. Это достаточно подробно отражено в книге [6], а также в работах [1; 7], где изучается проблема разработки тентовых тканевых конструкций. Подробный анализ приведенных там результатов приводит к задаче разработки эффективных методов приближенного решения уравнения минимальной поверхности и математическому обоснованию найденных методов в плане устойчивости и сходимости приближенных решений. Основная трудность при исследовании данных вопросов заключается в том, что уравнение минимальной поверхности является нелинейным, и поэтому традиционные методы, используемые для линейных уравнений, не пригодны. В работе [4] рассмотрен метод, который заключается в определении понятия кусочно-линейного решения минимальной поверхности над заданной триангуляцией расчетной области, и устанавливаются необходимые свойства этого решения. Именно, доказывается, что последовательность кусочно-линейных решений уравнения минимальных поверхностей будет сходиться к точному решению при условии, что функционал площади будет аппроксимироваться кусочно-линейными функциями с точностью 0(h ² ), где h — максимальная сторона треугольников триангуляции. Однако в трехмерном случае такой степени аппроксимации недостаточно. Для обоснования сходимости приближенных решений функционал площади должен быть приближен с точностью до 0(h 3 ). В этом случае предлагается использовать кусочно-квадратичные функции. Отметим также, что в работах [3; 8] получены оценки погрешности вычисления площади поверхностей для триангуляции частного вида, построенной по прямоугольной сетке.

1.    Основные результаты

Пусть Q С R” — ограниченная область. Рассмотрим функционал, задаваемый ин- тегралом

I (и) = У G(x,u, V u)dx, Ω

который определен для функций и Е С ² (Q). Отметим, что уравнение Эйлера — Лагранжа вариационной задачи для этого функционала имеет вид

N

Q[u] = £Х (x,u, V u)) - - G>,u, V u) = 0.              (2)

к=1

В случае когда подынтегральное выражение G(x,u, Vu) = ^/1 + |Vu|2, уравнением (2) является уравнение минимальной поверхности v-(

=, ^8х -

и

^— г

V 1 + |V u | ²

)01

Другим примером является уравнение Пуассона Au = /(х), которое соответствует функции G(x,u, V u) = |V u | ² + 2/(x)u(x).

Пусть задана многоугольная ограниченная область Q Е R2. Рассмотрим разбиение этого многоугольника на треугольники. Т1,Т2,...,TN. И пусть М1, М2,..., Мр — все вершины этих треугольников. Будем предполагать, что ни одна из точек М^ не является внутренней точкой ни одной из сторон треугольников (см. рис. 1). Через Г/ будем обозначать стороны всех треугольников, I = 1,2,...L, а максимальный диаметр всех треугольников обозначим через h, то есть h = max diamTk, где diam F =

= sup ( | x — у | : x, у Е F ), а _к — минимальный угол в треугольнике Т _к , а = min а _к >  0. к

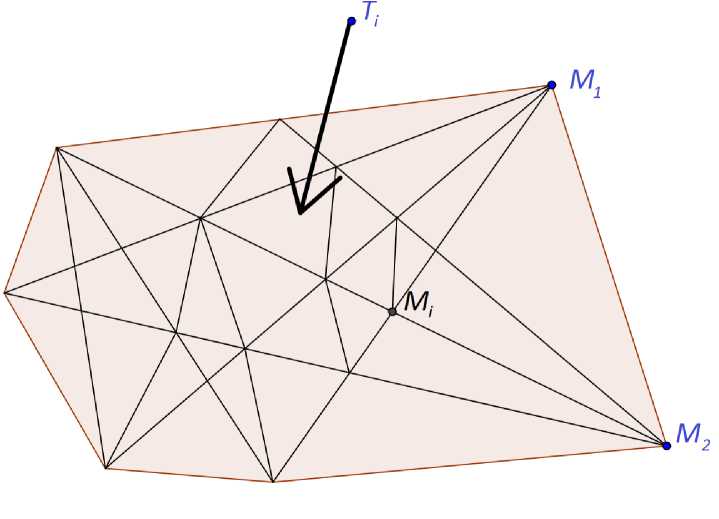
Рис. 1. Триангуляция области Ω

Для построения кусочно-квадратичной функции нужно к имеющимся вершинам треугольников М 1 ,М ₂ , ...,М _Р добавить середины всех сторон треугольников (см. рис. 2) и задать в них дополнительные значения функции и.

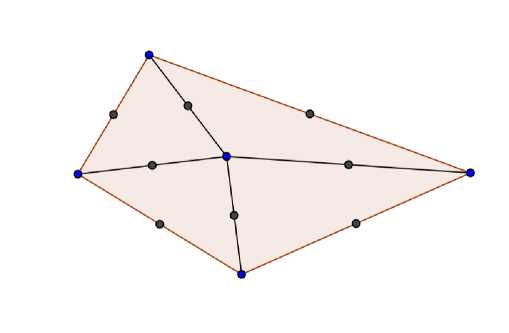
Рис. 2. Добавление середин сторон в каждом треугольнике

Пусть А 1 , А 2 ,..., А _т — получившийся набор точек, включая все середины сторон и вершины всех треугольников. Для произвольного набора значений и 1 ,и ₂ , ...и _т определим кусочно-квадратичную функцию и : Q ^ R так, что и(А . ) = и . , г = 1,...,m и функция и в каждом треугольнике T _k , к = 1,...,N , имеет вид: u(x 1 ,x ₂ ) = a _k x 2 + + 2b _k x 1 x ₂ + c _k x 2 + d _k x 1 + e _k x ₂ + f k . Данная функция будет непрерывной в Q. Прежде всего получим равенство, которое может бы т ь применено для произвольного интегрального функционала. Пусть функция f G С ² (Q). Обозначим через f ^N — кусочно-линейную функцию, такую что f ^N (М . ) = f (М^г = 1, 2...,m. Пусть g¹ = f ^N + t(f — f ^N ). Следующее утверждение дает формулу определения погрешности приближенного вычисления функционала.

Теорема 1. Предположим, что функция f G С 2 (Q) и f ^N — соответствующая кусочноквадратичная функция. Предположим, что для каждого внутреннего ребра произвольным образом выбрана нормаль ν . Тогда

N „            1

• 1    (f) — 1 (fN ) = Ё Iff-fN) / Ql»‘]dtdx + Gf — fN) Ё v. / G'ti(x,g‘, Vg^didS + k=1 t,          0              an          ‘=10

„

+ E ( У — f ^N ) E v   G_k (x,g + , V g + ) — G _t , (x,g - , V g - )dtdS,

внутр. rJrt          ‘=10

где g + ,g — — функция g¹, рассматриваемая в двух тетраэдрах с общей гранью Г ^ , причем g + соответствует тому тетраэдру, для которого нормаль v является внешней.

Доказательство. Рассмотрим разность

N                                          N 1  ,

1 (f ) — 1 (f ^N ) = ^ЕУ (G(x,f, V f) — G(x,f ^N , V f ^N ))dx = ^EJ J - (G(x,g', V g * ))dtdx =

= ^E i i [ d^G (f — f ^N )+ ^E dG (f — — ⁿ > - ■ ] ^-x^- = ^E it n (f — — ⁿ )^-x^-t + ^k =1i _k 0 L                    ‘ =1 -.              j           ^k =1T _k 0

+ ) ^E l^E dG (f — f ^N vx-t.

00 ^k =1T _k ‘=1

Рассмотрим отдельно интеграл

[ Ж. (f — f ^N ) - - ^dx.

Преобразуем его, воспользовавшись формулой Гаусса — Остроградского:

/If ; ^{( f — f N     x} = ^—_т^ dx, ( H;^(x' ,^g ' ^{( x )} , ^{V g} ‘ ^{( x ))} ) ^{( f — f N )dx +}/ Hi ^{(f — f N ) v} ‘ ^ds-

Тогда

N             / 1            ¹                                   \

^{1 (f} ) - ^{1 (f N} ) = E J^(f - ^{f N} )     du^{dxdt -} / 8хХж-^(x,9^t(x) ^ эКхУ^ dxdt ^ +

+ ^E / (f - f ^N ) ^E v , 1 ... ^k - ¹ 8T _k            ^{, -1} 0

Рассмотрим теперь отдельно интеграл по границе

E / (/ - / ^N ) E v , ¹ ц ^

к=1ЭТ _к            ^{, -1}    0

n 1

= /(/-/N) e/ dQ            ,-1 0

9G_ .

-— dtds + d Ч ,

n ¹

+ E   /( f - / ^N ) E v ,  (SC (x,9 + , ^ 9 + )

внутр. r < Г            , =1   0      ^{Ч г}

-

1У ^{( x,}9 - , ^ 9 ^ A ^dtds, ^д Ч г

где 9 + ,9 - — функции 9 ^t , рассматриваемые в треугольниках с общей гранью Г ^ , причем 9 + соответствует тому треугольнику, для которого нормаль v является внешней.

Таким образом, окончательно приходим к равенству

N                1                            n ¹

1 (/ ) - 1 (f ^N ) = ^E Iff - f ^N ) / Q|» ^t ]dtdx + Iff - f ^N ) ^E v, / G'_ti(x,_S ^t , ^ 9 ^t )dtdS + ^{t =1} T_1:                              d Q             ‘ -¹    0

”       ¹

+ E /( f - f ^N ) ^E v < / ^G t . (x,9 + , V g + )

^вну^тР^{. г}Г 1             ^, -¹    0

-С ч , (x,^ - , ^ 9 - )dtdS.

Далее нам понадобится оценка погрешности вычисления функции и ее производ-

ных в некотором треугольнике при условии, что данная функция приближается интерполируемым многочленом [2]. Итак, имеется некоторый треугольник А, каждая сторона которого разбита на I равных частей, и через точки разбиения проведены прямые L _q , параллельные сторонам треугольника. Стороны треугольников также будем относить к множеству прямых L _q . Обозначим через А множество, состоящее из точек пересечения этих прямых, лежащих в замкнутом треугольнике А. (Таким образом, А включает

также точки разбиения сторон треугольника и вершины треугольника.) Число таких

точек равно р = 1 + 2 + ... + (I + 1) = (I + 1)(1 + 2)/2. Будем обозначать их через

Q i (x 1 ,x 2 ), ...,Q n (x ^ ,x 2 ).

Ставится задача построения многочлена степени I

Р (xy,x 2 ) =  ^

Ш 1 + Ш 2 < 1

^ Ш 1 Ш 2

_ mi т ₂ x 1 x 2

принимающего в этих точках Q j (x { ,x ^l ₂ ) заданные значения

Р (x ^j ,x2) = f j ,3 = 1,...,п.                              (4)

Число неизвестных коэффициентов а _т 1 _т 2 также равно р, и, таким образом, соотношения (4) образуют систему р уравнений с р неизвестными. Если система (4) разрешима, то из нее могут быть найдены коэффициенты а _т 1 _т 2 . Для их нахождения можно выписать искомый многочлен Р ( х ) в явном виде.

Возьмем некоторую фиксированную точку Q 1 . Можно показать, что среди прямых L _q имеется ровно I прямых, удовлетворяющих следующему условию. Существует не более одной вершины треугольника, такой что Q 1 и эта вершина лежат по одну сторону от такой прямой. При этом оказывается, что каждая точка из Л , отличная от Q 1 , лежит на одной из таких прямых. На рисунке 3 эти прямые обозначены жирными линиями.

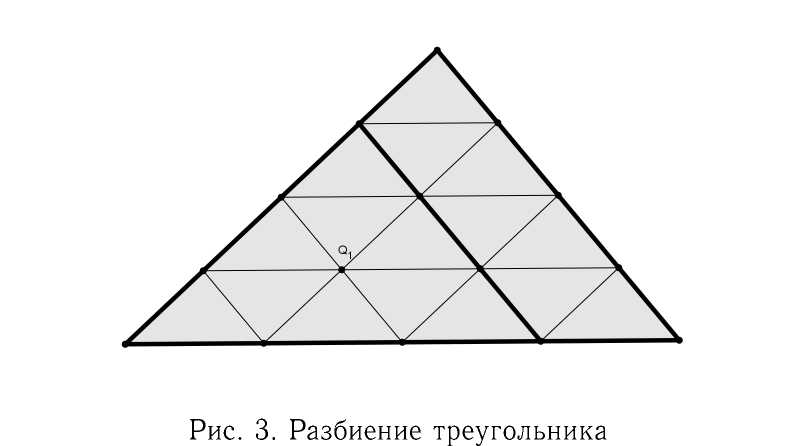
Пусть L j, ₁ (х ₁ ,х ₂ ) = 0, ...,L ,,£ (Х 1 , х ₂ ) = 0 — уравнения этих прямых. Функция

Ф , (Х 1 ,Х ₂ )= П L^T^ _г =1 L₃^ ( х 1 , х 2 )

является многочленом степени I, равна 1 в точке Q 1 и 0 в остальных точках Q ^ . Поэтому многочлен степени I

р

Р (Х 1 ,Х 2 ) = ^f ф , (Х 1 ,Ж 2 )

, =1

будет искомым. В случае, когда f , = f(ж { ,Х^г 2 ) при всех j , многочлен Р (ж 1 , х ₂ ) будет интерполяционным многочленом по отношению к f (ж 1 ,х ₂ ).

Утверждение 1. Значения многочлена Р (Х 1 , х ₂ ) на каждой из сторон треугольника зависят от значений f , , соответствующих точкам Q , этой стороны.

Утверждение 2. Пусть h — это длина максимальной из сторон треугольника А , f , = f (Q , ) , f — некоторая гладкая функция,

M _l+1 = max max T i + г 2 = £ +1 A

д ^{1 +1} f (Х 1 ,Х 2 ) дХр дХ?

α — наименьший из углов треугольника. Тогда справедлива оценка max |f (Х1 ,Х2) - Р(Х1, Х2)| < Ca,iMi+1 hm, где Ca,£ - постоянная, зависящая только от I и а.

Утверждение 3. При выполнении условия утверждения 2 для 0 < т 1 + т ₂ < I + 1 справедлива оценка

max

Δ

д^т^ ^т^ ² / (х^) д ^т 1 + ^т 2 Р (Х 1 ,Х 2 ) дх? дх 2         дх? дх 2 ²

В частности, max |V / — V P | <  V2C a ,i M i +i ^ ¹ .

< С а М^^{1 - 1 - 2} .

2. Основные результаты

Применим доказанное равенство в теореме 1 для оценки погрешности вычисления площади графика функции

^{1 ( /}^ = / I V ^{1 +} ^ ⁺ ^^dX 1 ^dX 2

в случае плоской области Q С R ² . Пусть / G С ² (Q). Положим М 1 = max max | / _L. (х) | ,

1 < г < 2 Q

М 2 = max max I / _LL (х) | . Получим оценку для значений оператора

1 < г < 2 Q ¹³

W] = Е G ‘ W, V g ¹ ))^ — G' _{g t} (х,^, V g ¹ ). г=1

Ясно, что

^gt (х,д, Vg1)=0, так как G зависит только от Vg1. Тогда

dG =     gL г д ^г  V1+1WP’

Таким образом,

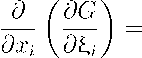
gL_x• • (1 + IVg¹ 1 ² ) — д_ж. ^ д_ж. • д_{ж ж}.

-^-г^-г                                       '-'.i-г         ^ 3Lq      ^-ьг.L^

3=1

(1 + IV g ¹ 1 ² ) ²

Q|g‘] = Е г=1

g - г - г •^{(1 +} \^V g^{t | 2 ) —} g L г Е g L ₅ • g L г - ₅ 3=1

(1 + IV g ¹ 1 ² ) ²

= Е g L г - ₃ г,3=1        \

⁽¹ + ^|V g ^{1 | 2 )} 5 гз ^— g - г g L j (1 + IV g ¹ 1 ² ) ²

)

Тогда для всех i,j = 1, 2 имеем

Q¹ У L г L j

⁽¹ + ^|V g ^{1 | 2 )} 5 г,- ^— g L г g L j (1 + IV g ¹ 1 ² ) ²

< ^{| 9} Х _iXj I • (⁽¹ + ^V k 2 ) + Wx 1 9x j l) <  ^M 2 ⁽¹ + (M i + V ^{2 C}a 2 ^M3^{h 2 ) 2)}.

Поэтому

№41

^2.^ (1 + |V 9 ⁺ 1 )&ti9x 9x-

E "----,    ' j,2'3 — 9l..j < 4M2(1 + (Mi + V2C„,2m ■ i,j=i       (1 + |V9x| )2           3

Далее ясно, что

E v > ^=1    0

9 ^х . dt x %

V ((1 + |V 9 ^x | ² ))

< |v| •

V9 ^x VCk+Wn)

< 1 .

Зафиксируем внутреннее ребро Г ^ . Обозначим через Т + и Т _- треугольники, соприкасающиеся по этому ребру. Тогда на Г выполнено V 9 + — V 9 - = ( V / ^N ) | т ₊ — ( V / ^N ) | т _ . Поэтому

V 9 +           VgL

Vk+IWk У(ТТЖП

< 2 IV 9 + — V 9 - 1 = 2 | ( V / ^N )k — ( V / ^N ) | т - 1 .

Воспользуемся утверждением 3, где показано, что градиенты функции / ^N и / удовлетворяют неравенству |V / — V / ^N I <  V2C a , 2 M ? h ² . Тогда

∑︁ г=1

⁽ 9+ k           ⁽ 9-k

< W2C a ,2 M ? h².

V (1 + IV 9 + 1 ² )    V (1 + IV 9 - 1 ² )

Положим 4V2C _a , ₂ M ? h² = C 1 . Применяя все приведенные неравенства к равенству (3), получим

| I (/ ^N ) — I (/) |<

< max |/ — /N| I 4M2(1 + (Mi + V2Ca,2M?h2)2)|Q| + |dQ| + Cih2   E   |ГгI внутр.r^

где |Q| — площадь фигуры Q, а |dQ| — ее периметр. Мы можем предположить, что триангуляция обладает таким свойством, что найдется постоянная C2, независящая от h, для которой   ^2   |r^|h < C2. Таким образом, мы пришли к неравенству внутр.г^

|I(/N) — I(/)|

C? = 4M2(1 + (Mi + V2Ca,2M?h²)²)|Q| + |dQ| + CiC2h.

Далее несложно показать, что из Утверждения 2 следует, что |/^N— /1 < C_a,₂M?h?. Таким образом, окончательно приходим к следующей оценке

|I(/^N) — I(/)| <Ca,2C?M?h?.

Рассмотрим следующий пример, в котором мы вычисляем постоянные C2 и a, зависящие от триангуляции. Пусть Q = [a, b] х [с, d] и а = ж0 < х1 < ... < хт = Ь,с = ^0 < < у1 < ... < ут = d, где Хг = а + z(b — а)/т, yj = с + j(d — с)/т. Тогда Q разбивается на прямоугольники Q^j = [xj,Xj+1] х [yj,yj+1], 0 < i < m — 1,0 < j < m — 1. Далее разделим каждый такой прямоугольник правой или левой диагональю. Тогда

/     / d — c\       fb — a\\ a = min

(arctg ^ )-arctg (—JJ,

С = m—1 D((b — a) + (d — c)) + D2 < DID + P/2), m где D = ^/(b — a)2 + (d — c)2 — длина диагонали прямоугольника, а P = 2(b — a + d — — c) — его периметр.

Заключение

В данной работе рассматривался вопрос об оценки точности кусочно-квадратичной аппроксимации площади С²-гладкой поверхности. В результате была получена оценка степени приближения |7(f^N) — I(f)| < С_а,₂С3М3К³. Таким образом, порядок аппроксимации оказался выше на порядок, чем в случае, рассмотренном в работе [5].